Mohr Circle n In 2 D space e























- Slides: 30

Mohr Circle n In 2 D space (e. g. , on the s 1 s 2 , s 1 s 3, or s 2 s 3 plane), the normal stress (sn) and the shear stress (ss), could be given by equations (1) and (2) in the next slides n Note: The equations are given here in the s 1 s 2 plane, where s 1 is greater than s 2. n If we were dealing with the s 2 s 3 plane, then the two principal stresses would be s 2 and s 3

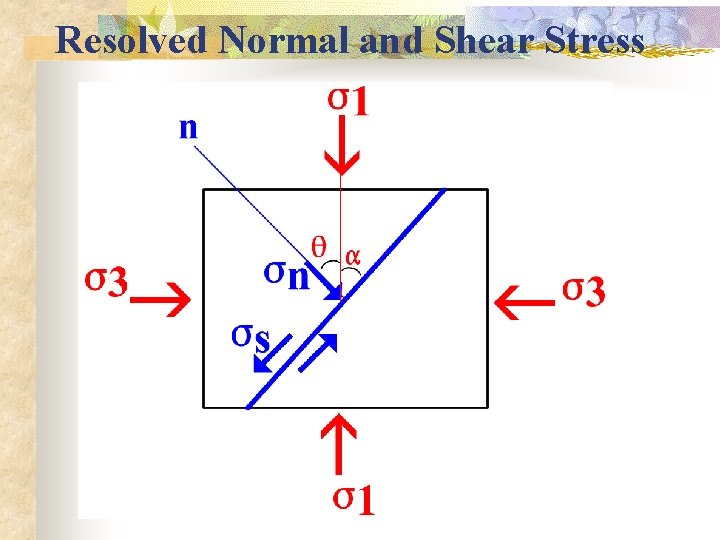
Normal Stress The normal stress, sn: sn= (s 1+s 2)/2 + (s 1 -s 2)/2 cos 2 q n (1) In parametric form the equation becomes: sn = c + r cosω Where n c = (s 1+s 2)/2 is the center, which lies on the normal stress axis (x axis) n r = (s 1 -s 2)/2 is the radius n ω= 2 q

Sign Conventions sn is compressive when it is “+”, i. e. , when sn>0 sn is tensile when it is “-”, i. e. , when sn< 0 sn= (s 1+s 2)/2+(s 1 -s 2)/2 cos 2 q NOTE: q is the angle from s 1 to the normal to the plane! n = 1 at q = 0 o n = 2 at q = 90 o n (a maximum) (a minimum ) There is no shear stress on the three principal planes (perpendicular to the principal stresses)

Resolved Normal and Shear Stress

Shear Stress The shear stress ss = (s 1 -s 2)/2 sin 2 q n (2) In parametric form the equation becomes: ss = r sinω where ω = 2 q s > 0 represents left-lateral shear s < 0 represents right-lateral shear s = 0 at q = 0 o or 90 o or 180 o (a min) s = ( 1 - 2)/2 at q = + 45 o (maximum shear stress) n The maximum s is 1/2 the differential stress

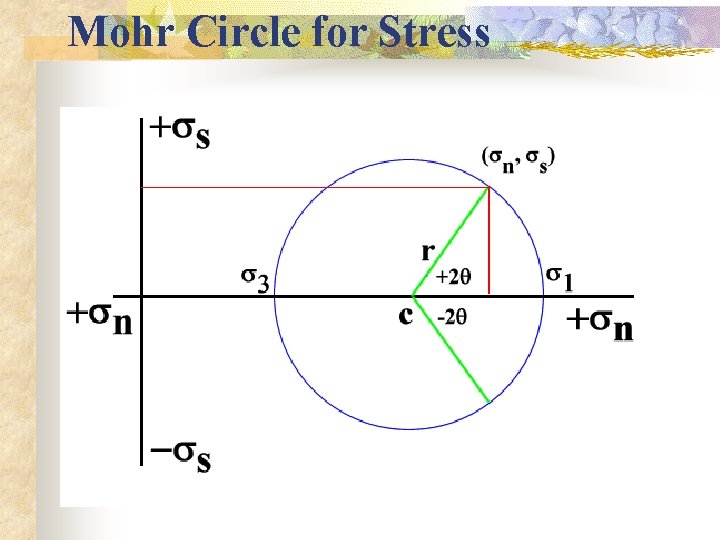
Construction of the Mohr Circle in 2 D n Plot the normal stress, sn, vs. shear stress, on a graph paper using arbitrary scale (e. g. , mm scale!) n Calculate: n Center c = (s 1+s 2)/2 n Radius r = (s 1 -s 2)/2 n Note: Diameter is the differential stress ( 1 - 2) n The circle intersects the sn (x-axis) at the two principal stresses (s 1 and s 2)

Construction of the Mohr Circle n n Multiply the physical angle q by 2 The angle 2 q is from the cs 1 line to any point on the circle +2 q (CCW) angles are read above the x-axis -2 q (CW) angles below the x-axis, from the s 1 axis n The sn and ss of a point on the circle represent the normal and shear stresses on the plane with the given 2 q angle n NOTE: The axes of the Mohr circle have no geographic significance!

Mohr Circle for Stress.

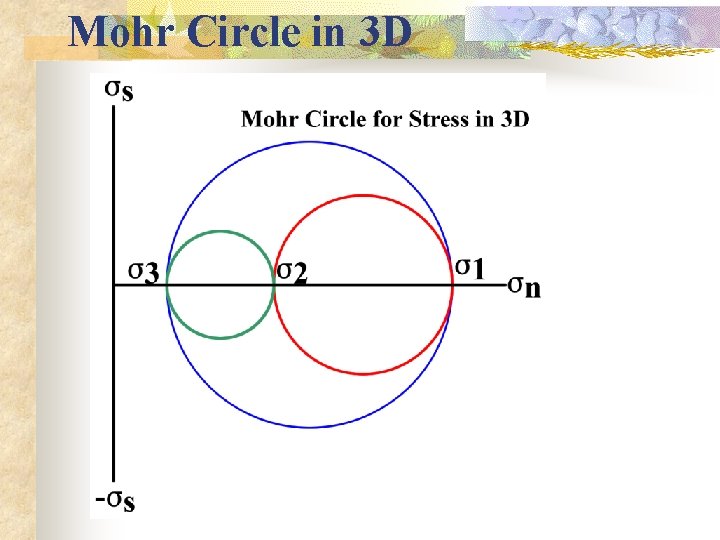
Mohr Circle in 3 D

Maximum & Minimum Normal Stresses The normal stress: sn= (s 1+s 2)/2 + (s 1 -s 2)/2 cos 2 q NOTE: q (in physical space) is the angle from s 1 to the normal to the plane When q = 0 o then cos 2 q = 1 and sn=(s 1+s 2)/2 + (s 1 -s 2)/2 which reduces to a maximum value: sn= (s 1+s 2 + s 1 -s 2)/2 sn= 2 s 1/2 sn= s 1 When q = 90 o then cos 2 q = -1 and sn= (s 1+s 2)/2 - (s 1 -s 2)/2 which reduces to a minimum sn= (s 1+s 2 - s 1+s 2)/2 sn= 2 s 2/2 sn= s 2

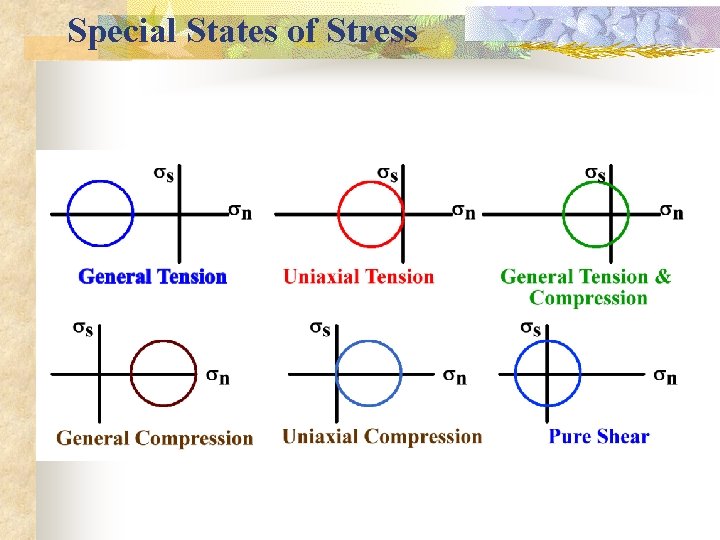
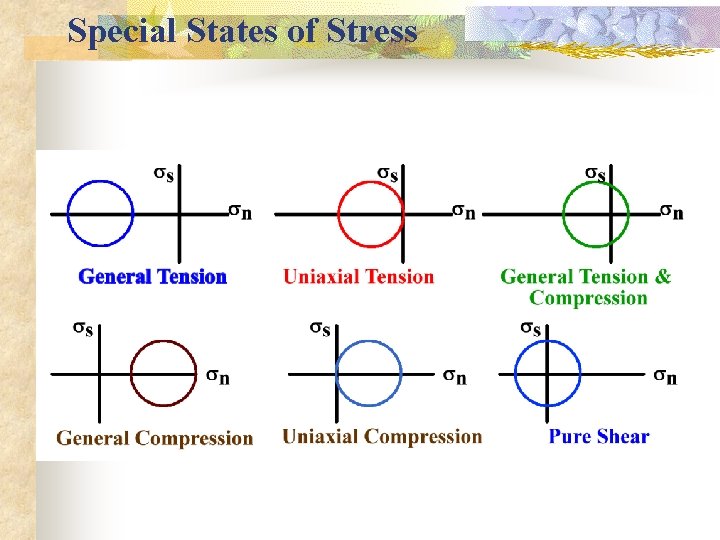
Special States of Stress - Uniaxial Stress n Uniaxial Stress (compression or tension) n One principal stress ( 1 or 3) is non-zero, and the other two are equal to zero Uniaxial compression Compressive stress in one direction: s 1 > s 2=s 3 = 0 |a 0 0| |0 0 0| n The Mohr circle is tangent to the ordinate at the origin (i. e. , s 2=s 3= 0) on the + (compressive) side n

Special States of Stress

Uniaxial Tension in one direction: 0 = s 1 = s 2 > s 3 |0 |0 |0 n 0 0| 0 -a| The Mohr circle is tangent to the ordinate at the origin on the - (i. e. , tensile) side

Special States of Stress - Axial Stress n Axial (confined) compression: s 1 > s 2 = s 3 > 0 |a 0 0| |0 b 0| |0 0 b| n Axial extension (extension): s 1 = s 2 > s 3 > 0 |a 0 0| |0 a 0| |0 0 b| n The Mohr circle for both of these cases are to the right of the origin (non-tangent)

Special States of Stress - Biaxial Stress n n n Biaxial Stress: n Two of the principal stresses are non-zero and the other is zero Pure Shear: s 1 = -s 3 and is non-zero (equal in magnitude but opposite in sign) s 2 = 0 (i. e. , it is a biaxial state) n The normal stress on planes of maximum shear is zero (pure shear!) |a 0 0 | |0 0 -a| The Mohr circle is symmetric w. r. t. the ordinate (center is at the origin)

Special States of Stress

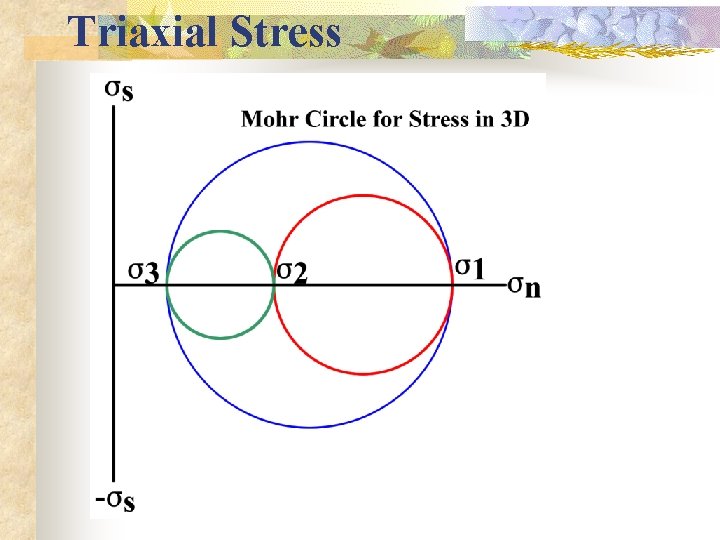
Special States of Stress - Triaxial Stress n Triaxial Stress: n s 1, s 2, and s 3 have non-zero values n s 1 > s 2 > s 3 and can be tensile or compressive n Is the most general state in nature |a 0 0 | |0 b 0 | |0 0 c | n The Mohr circle has three distinct circles

Triaxial Stress

Two-dimensional cases: General Stress n General Compression n n Both principal stresses are compressive n is common in earth) General Tension n n Both principal stresses are tensile Possible at shallow depths in earth

Isotropic Stress n The 3 D, isotropic stresses are equal in magnitude in all directions (as radii of a sphere) n Magnitude = the mean of the principal stresses sm= (s 1+s 2+s 3)/3 = (s 11+s 22+s 33 )/3 P = s 1= s 2= s 3 when principal stresses are equal n i. e. , it is an invariant (does not depend on a specific coordinate system). No need to know the principal stress; we can use any! Leads to dilation (+ev & -ev); but no shape change n ev=(v´-vo)/vo= v/vo [no dimension] n v´ and vo are final and original volumes

Stress in Liquids n Fluids (liquids/gases) are stressed equally in all directions (e. g. magma); e. g. : n Hydrostatic, Lithostatic, Atmospheric pressure n All of these are pressure due to the column of water, rock, or air, respectively: P = rgz n n n z is thickness r is density g is the acceleration due to gravity

Hydrostatic Pressure- Hydrostatic Tension n n n Hydrostatic Pressure: s 1 = s 2 = s 3 = P |P 0 0| |0 P 0| |0 0 P| All principal stresses are compressive and equal (P) No shear stress exists on any plane All orthogonal coordinate systems are principal coordinates Mohr circle reduces to a point on the sn axis Hydrostatic Tension n The stress across all planes is tensile and equal n There are no shearing stresses n Is an unlikely case of stress in the earth

Deviatoric Stress n A total stress s. T can be divided into its components: n isotropic (Pressure) or mean stress (sm) n n Pressure is the mean of the principal stresses (may be neglected in most problems). Only causes volume change. deviatoric (sd) that deviates from the mean n Deviator’s components are calculated by subtracting the mean stress (pressure) from each of the normal stresses of the general stress tensor (not the shear stresses!). Causes shape change and that it the part which we are most interested in. s. T=sm+sd or sd=s. T-sm

Confining Pressure n In experimental rock deformation, pressure is called confining pressure, and is taken to be equal to the 2 and 3 (uniaxial loading) n This is the pressure that is hydraulically applied around the rock specimen n In the Earth, at any point z, the confining pressure is isotropic (lithostatic) pressure: P = rgz

Decomposition of Matrix • Decomposition of the total stress matrix into the mean and deviatoric matrices • The deviatoric part of total stress leads to change in shape

Example - Deviatoric & Mean stress Given: s 1 = 8 Mpa, s 2 = 5 Mpa, and s 3 = 2 Mpa Find the mean and the diviatoric stresses The mean stress (sm): sm = (8 + 5 + 2) / 3 = 5 MPa The deviatoric stresses (sn ): s 1 = 8 -5 = 3 Mpa (compressive) s 2 = 5 -5 = 0 Mpa s 3 = 2 -5 = -3 Mpa (tensile)

Differential Stress The difference between the maximum and the minimum principal stresses (s 1 -s 2) n Is always positive n Its value is: n twice the radius of the largest Mohr circle n It is twice the maximum shear stresses Note: ss = (s 1 -s 2)/2 sin 2 q n s = ( 1 - 2)/2 at q = + 45 o (a maximum) n The maximum s is 1/2 the differential stress n Is an invariant of the stress tensor

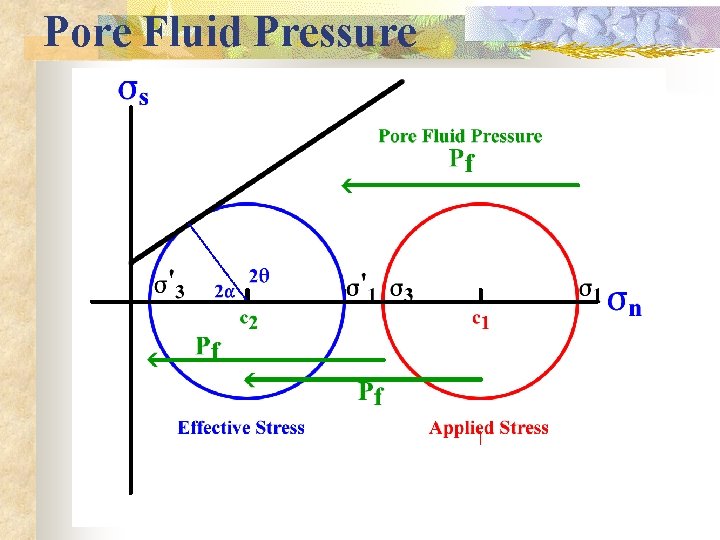
Effective Stress n Its components are calculated by subtracting the internal pore fluid pressure (Pf) from each of the normal stresses of the external stress tensor n This means that the pore fluid pressures opposes the external stress, decreasing the effective confining pressure n The pore fluid pressure shifts the Mohr circle toward lower normal stresses. This changes the applied stress into an effective stress

Effective Stress n (applied stress - pore fluid pressure)= effective stress |s 11 s 12 s 13 | | Pf 0 0 | |s 11 - Pf s 12 s 13 | |s 21 s 22 s 23 | - | 0 Pf 0 |=|s 21 s 22 – Pf s 23 | |s 31 s 32 s 33 | | 0 0 Pf | |s 31 s 32 s 33 - Pf | n Mechanical behavior of a brittle material depends on the effective stress, not on the applied stress

Pore Fluid Pressure
 Mohrs circle equation
Mohrs circle equation Hydrostatic compression mohr's circle
Hydrostatic compression mohr's circle Stress transformation
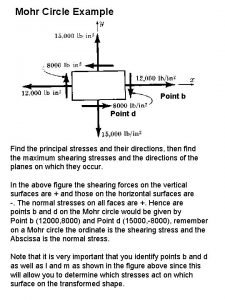
Stress transformation Mohr's circle example
Mohr's circle example Shear capacity
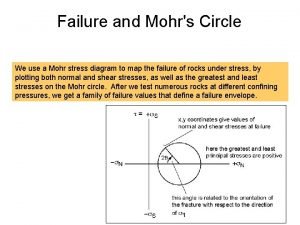
Shear capacity Mohr diagram geology
Mohr diagram geology Diagram mohr
Diagram mohr Mohr's circle transformation equations
Mohr's circle transformation equations Strain transformation
Strain transformation Circle a is tangent to circle b. true false
Circle a is tangent to circle b. true false Finkster definition
Finkster definition Circle j is congruent to circle p
Circle j is congruent to circle p No more than sign
No more than sign Mohr
Mohr Gordon mohr
Gordon mohr Maxence mohr
Maxence mohr Gunnar mohr
Gunnar mohr Brittle coulomb mohr theory
Brittle coulomb mohr theory Reiter balanza
Reiter balanza Micropipette parts
Micropipette parts Metodo di mohr
Metodo di mohr Dilatanza geotecnica
Dilatanza geotecnica Criterio de tresca
Criterio de tresca Tensão de cisalhamento
Tensão de cisalhamento Metode mohr
Metode mohr Mpa
Mpa Tricercle de mohr
Tricercle de mohr Maxence mohr
Maxence mohr Sarotti-mohr werbung
Sarotti-mohr werbung Mohr yöntemi
Mohr yöntemi George nees
George nees