Mohrs circle for plane stress The transformation equations

Mohr’s circle for plane stress • The transformation equations for plane stress can be represented in graphical form by a plot known as Mohr’s circle • This graphical representation is extremely useful because it enables you to visualize the relationships between the normal and shear stresses acting on various inclined planes at a point in a stressed body • Using Mohr’s circle you can also calculate principal stresses, maximum shear stresses and stresses on inclined planes • Mohr’s circle is also valid for strains and moments of inertia * Mohr’s circle is named after the famous German civil engineer Otto Christian Mohr (1835 -1918), who developed the circle in 1882

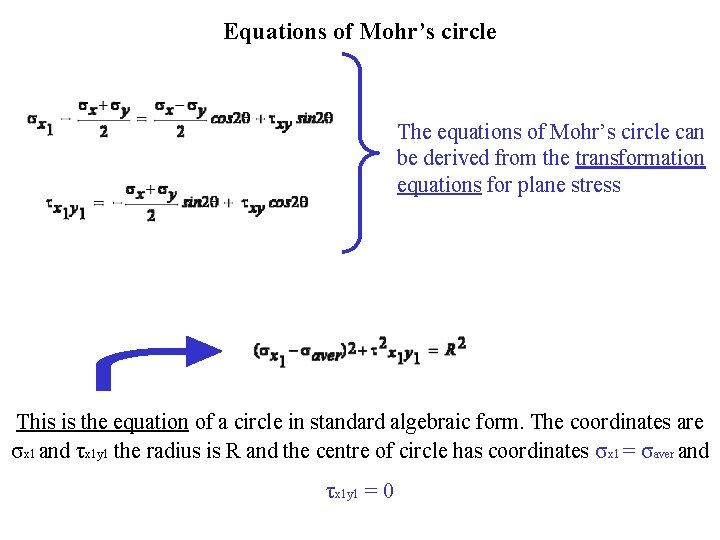
Equations of Mohr’s circle The equations of Mohr’s circle can be derived from the transformation equations for plane stress This is the equation of a circle in standard algebraic form. The coordinates are σx 1 and τx 1 y 1 the radius is R and the centre of circle has coordinates σx 1 = σaver and τx 1 y 1 = 0

Two forms of Mohr’s circle • Mohr's circle can be plotted from the previous equations in either of two forms. • In the first form of Mohr’s circle, we plot the normal stress σx 1 positive to the right and the shear stress τx 1 y 1 positive downward (fig 7 -14 a). The advantage of plotting shear stress positive downward is that the angle 2θ will be positive when counterclockwise, which agrees with the positive direction of 2θ • In the second form of Mohr’s circle, τx 1 y 1 is plotted positive upward but the angle 2θ is now positive clockwise (fig 7 -14 b), which is opposite to its usual positive direction Both forms of Mohr’s circle can be used. However, it is easier to visualize the orientation of the stress element if the positive direction of the angle 2θ is the same in the Mohr’s circle as it is for the element itself. Therefore, we will choose the first form of Mohr’s circle.

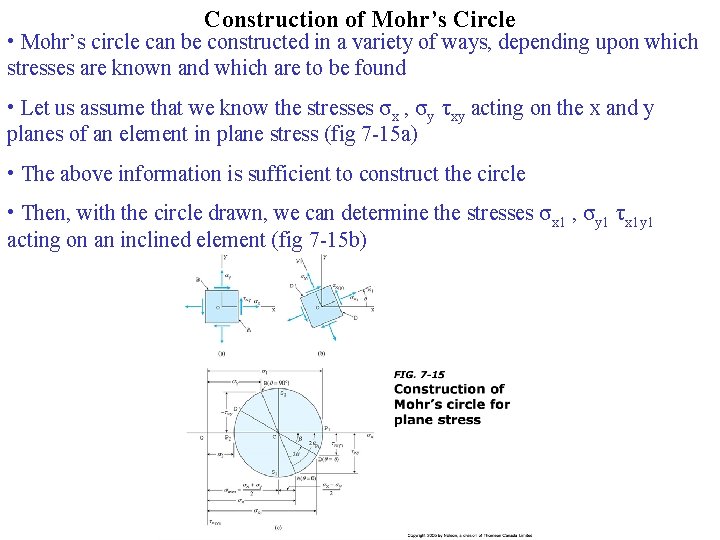
Construction of Mohr’s Circle • Mohr’s circle can be constructed in a variety of ways, depending upon which stresses are known and which are to be found • Let us assume that we know the stresses σx , σy τxy acting on the x and y planes of an element in plane stress (fig 7 -15 a) • The above information is sufficient to construct the circle • Then, with the circle drawn, we can determine the stresses σx 1 , σy 1 τx 1 y 1 acting on an inclined element (fig 7 -15 b)

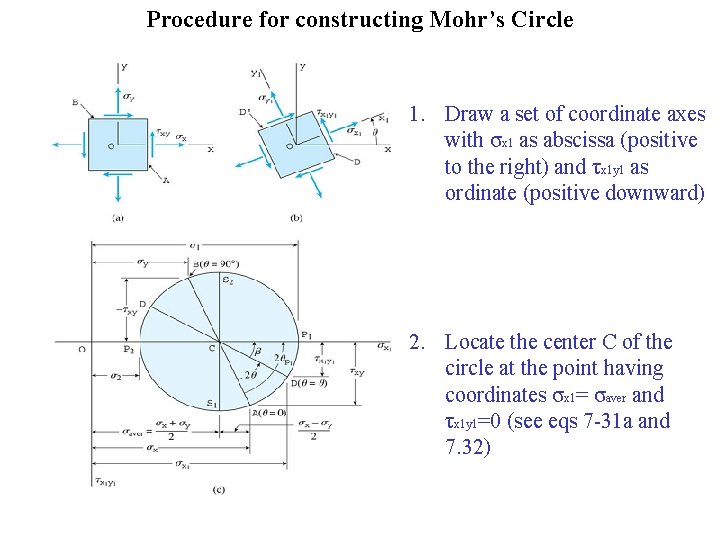
Procedure for constructing Mohr’s Circle 1. Draw a set of coordinate axes with σx 1 as abscissa (positive to the right) and τx 1 y 1 as ordinate (positive downward) 2. Locate the center C of the circle at the point having coordinates σx 1= σaver and τx 1 y 1=0 (see eqs 7 -31 a and 7. 32)

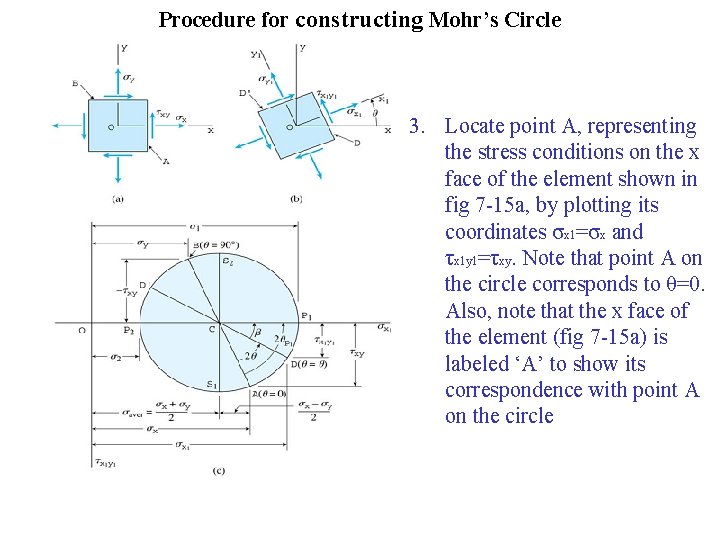
Procedure for constructing Mohr’s Circle 3. Locate point A, representing the stress conditions on the x face of the element shown in fig 7 -15 a, by plotting its coordinates σx 1=σx and τx 1 y 1=τxy. Note that point A on the circle corresponds to θ=0. Also, note that the x face of the element (fig 7 -15 a) is labeled ‘A’ to show its correspondence with point A on the circle

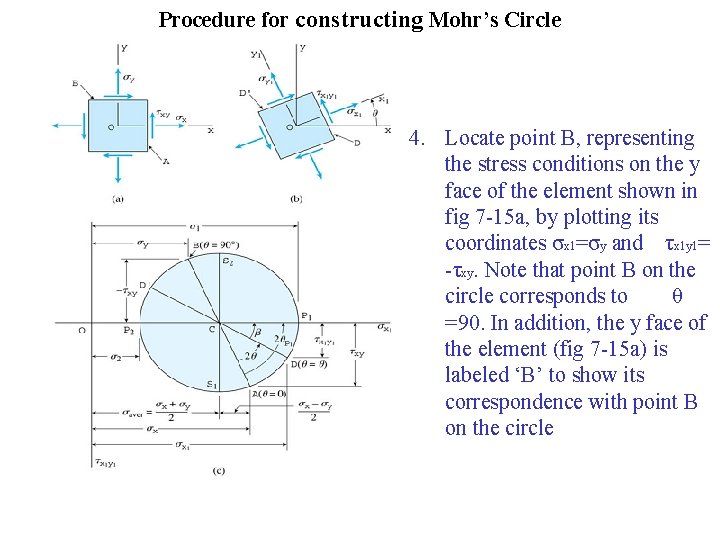
Procedure for constructing Mohr’s Circle 4. Locate point B, representing the stress conditions on the y face of the element shown in fig 7 -15 a, by plotting its coordinates σx 1=σy and τx 1 y 1= -τxy. Note that point B on the circle corresponds to θ =90. In addition, the y face of the element (fig 7 -15 a) is labeled ‘B’ to show its correspondence with point B on the circle

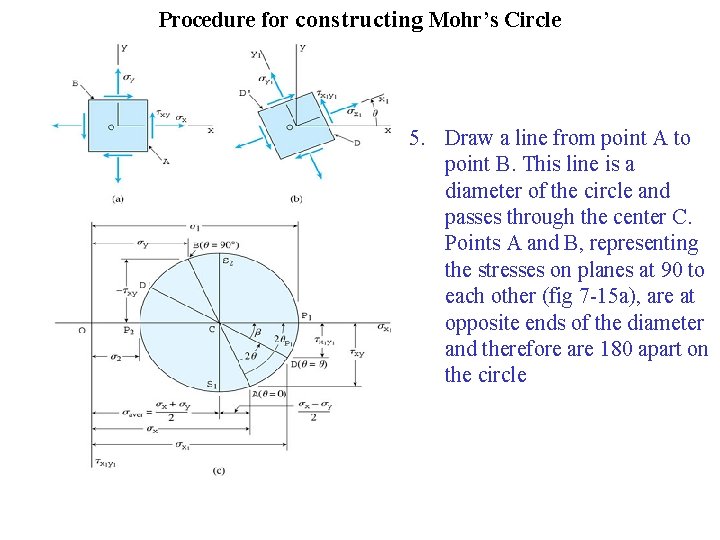
Procedure for constructing Mohr’s Circle 5. Draw a line from point A to point B. This line is a diameter of the circle and passes through the center C. Points A and B, representing the stresses on planes at 90 to each other (fig 7 -15 a), are at opposite ends of the diameter and therefore are 180 apart on the circle

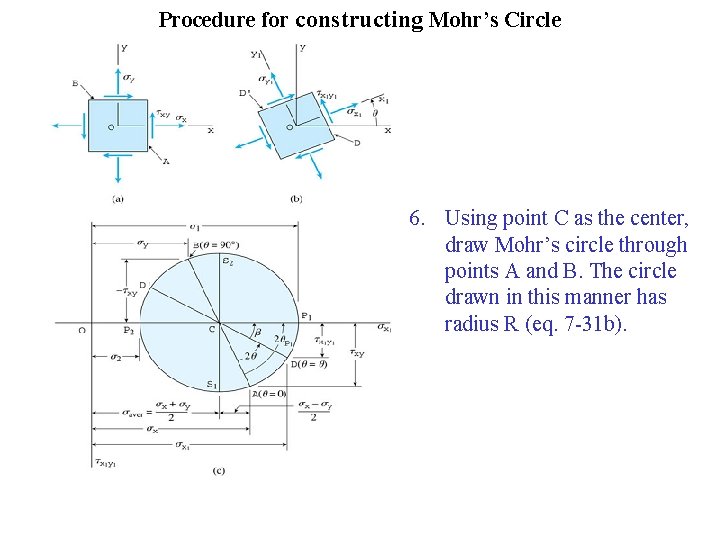
Procedure for constructing Mohr’s Circle 6. Using point C as the center, draw Mohr’s circle through points A and B. The circle drawn in this manner has radius R (eq. 7 -31 b).

Example At a point on the surface of a pressurized cylinder, the material is subjected to biaxial stresses σx = 90 MPa and σy = 20 MPa, as shown on the stress element on fig 7 -17 a. Using Mohr’s circle, determine the stresses acting on an element inclined at an angle θ = 30. (consider only the in-plane stresses, and show the results on a sketch of a properly oriented element. )

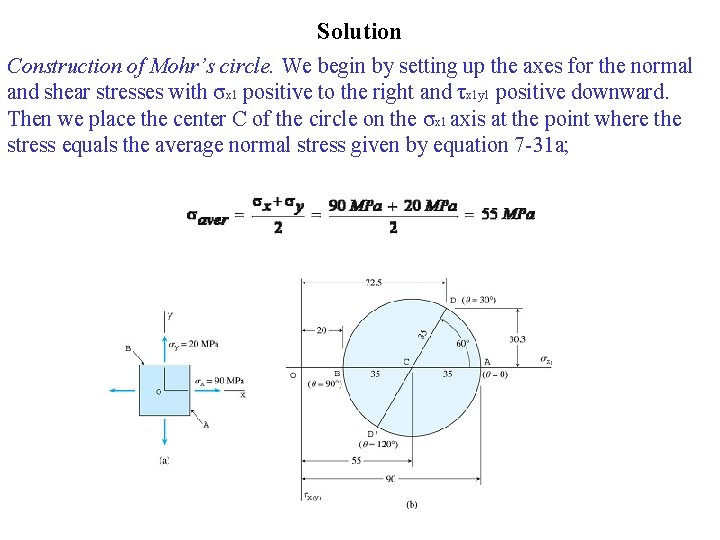
Solution Construction of Mohr’s circle. We begin by setting up the axes for the normal and shear stresses with σx 1 positive to the right and τx 1 y 1 positive downward. Then we place the center C of the circle on the σx 1 axis at the point where the stress equals the average normal stress given by equation 7 -31 a;

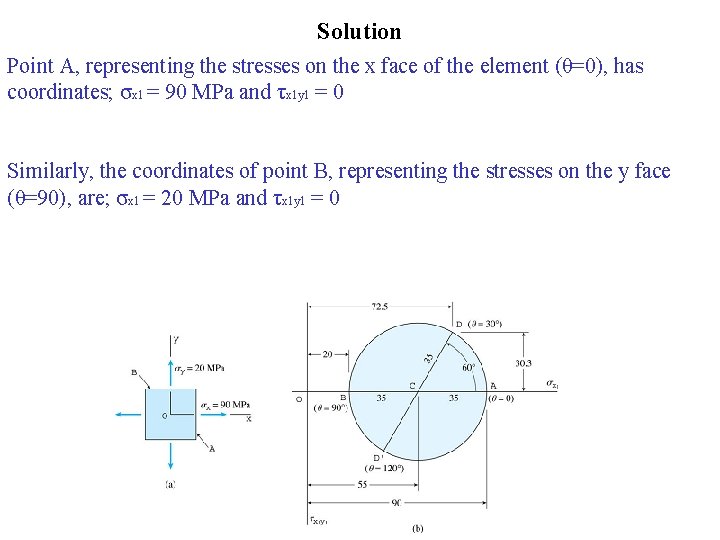
Solution Point A, representing the stresses on the x face of the element (θ=0), has coordinates; σx 1 = 90 MPa and τx 1 y 1 = 0 Similarly, the coordinates of point B, representing the stresses on the y face (θ=90), are; σx 1 = 20 MPa and τx 1 y 1 = 0

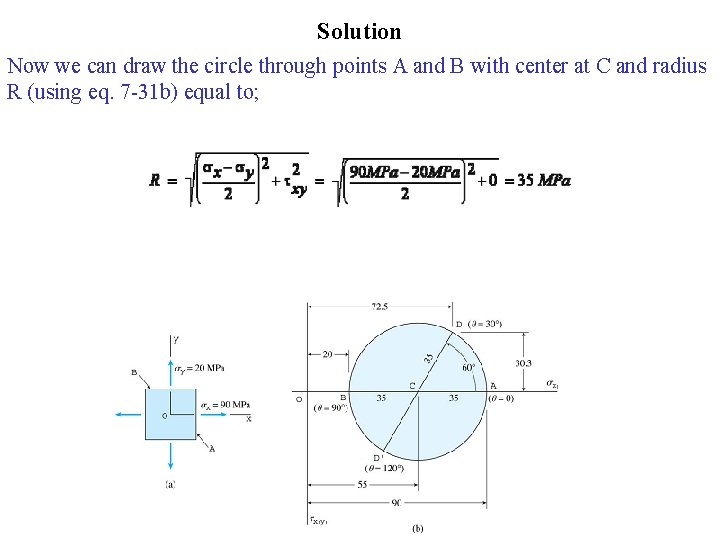
Solution Now we can draw the circle through points A and B with center at C and radius R (using eq. 7 -31 b) equal to;

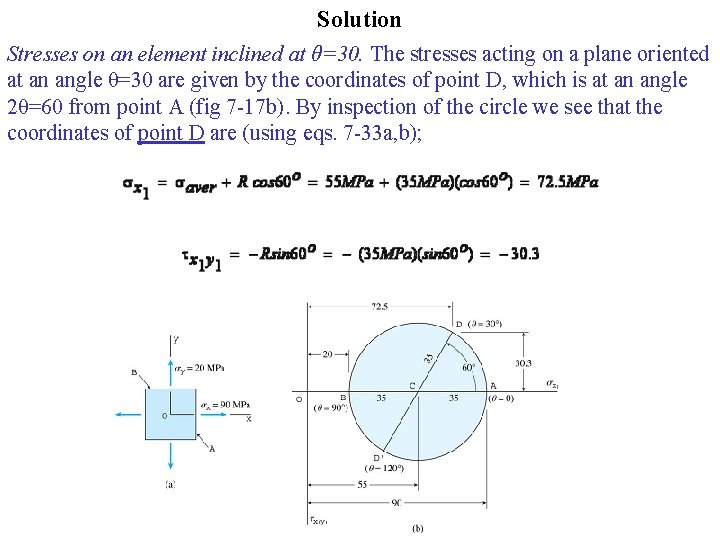
Solution Stresses on an element inclined at θ=30. The stresses acting on a plane oriented at an angle θ=30 are given by the coordinates of point D, which is at an angle 2θ=60 from point A (fig 7 -17 b). By inspection of the circle we see that the coordinates of point D are (using eqs. 7 -33 a, b);

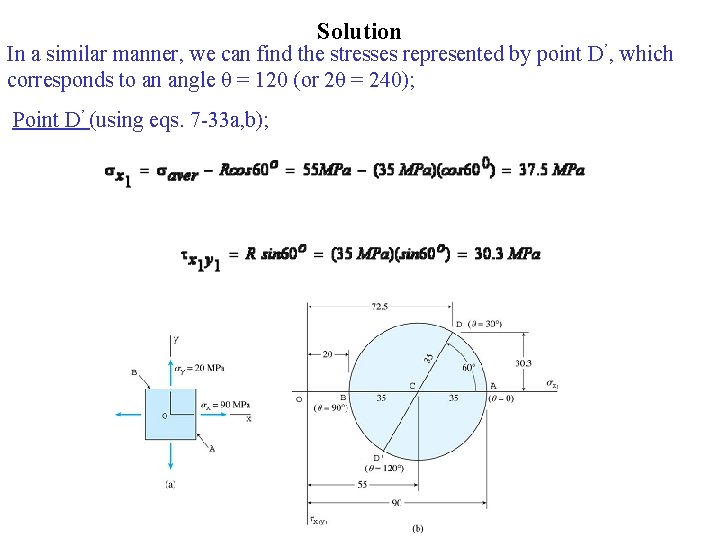
Solution In a similar manner, we can find the stresses represented by point D’, which corresponds to an angle θ = 120 (or 2θ = 240); Point D’ (using eqs. 7 -33 a, b);

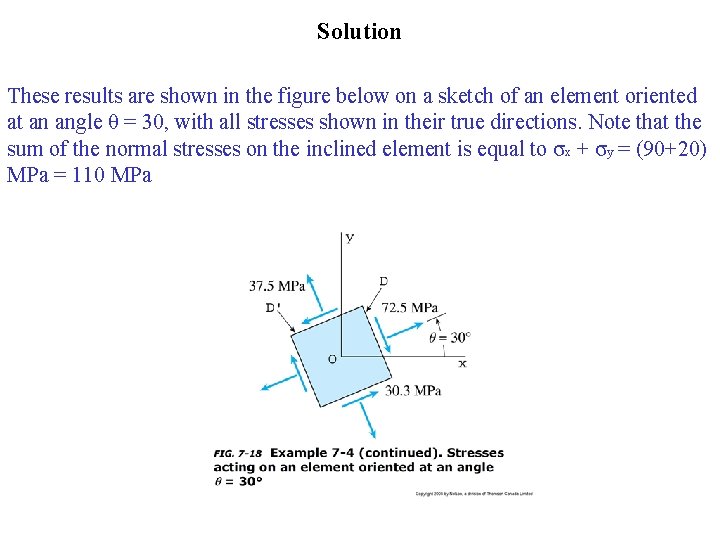
Solution These results are shown in the figure below on a sketch of an element oriented at an angle θ = 30, with all stresses shown in their true directions. Note that the sum of the normal stresses on the inclined element is equal to σx + σy = (90+20) MPa = 110 MPa