GEOMETRICAL DEFINITION OF A CIRCLE A circle is













- Slides: 24


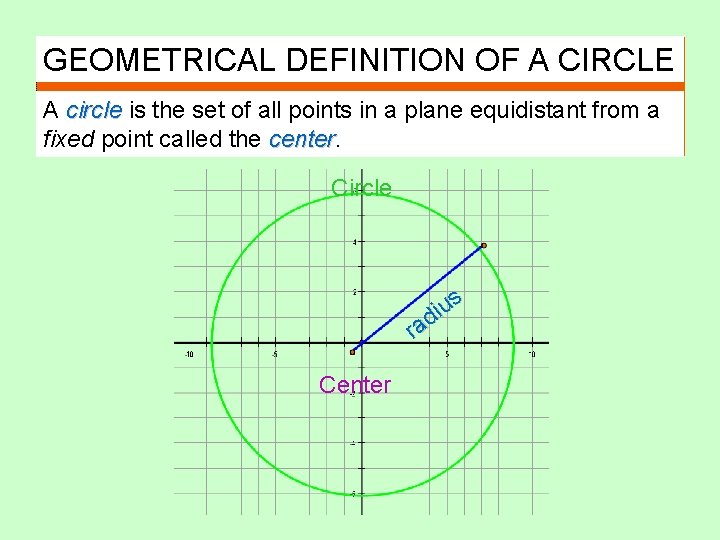
GEOMETRICAL DEFINITION OF A CIRCLE A circle is the set of all points in a plane equidistant from a fixed point called the center Circle s u i d ra Center

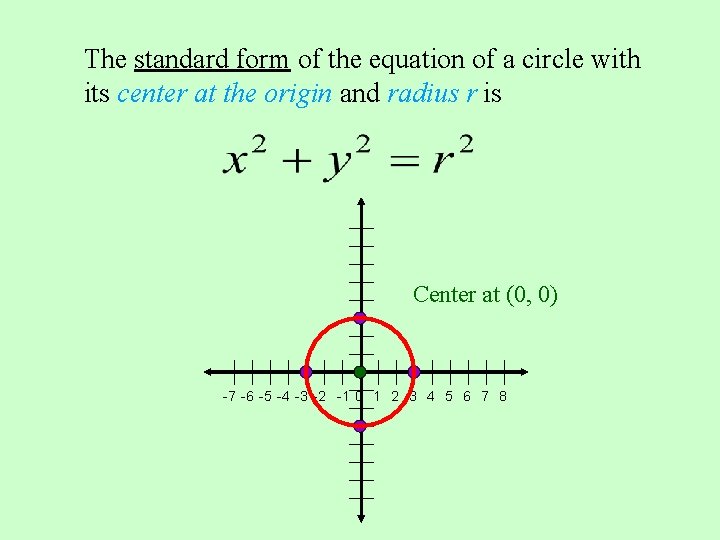
The standard form of the equation of a circle with its center at the origin and radius r is Center at (0, 0) -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8

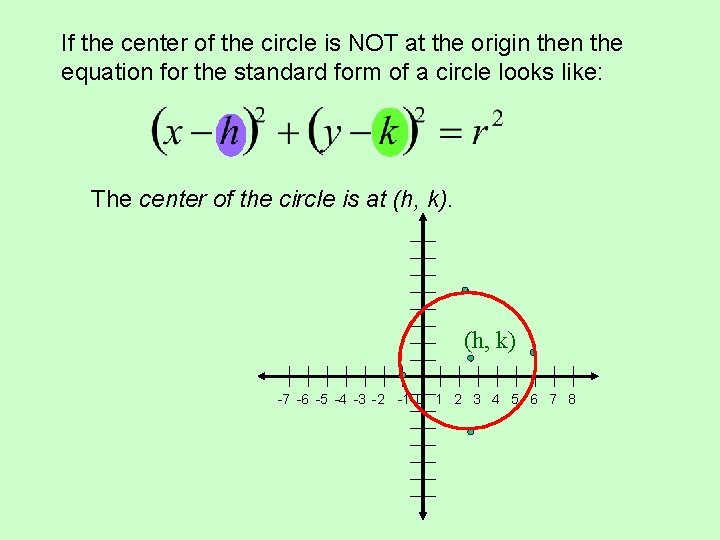
If the center of the circle is NOT at the origin the equation for the standard form of a circle looks like: The center of the circle is at (h, k) -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8

(2) General equation of a circle is x 2 + y 2 + Dx + Ey + F = 0 Note: The given quadratic relation will be a circle if the coefficients of the x 2 term and y 2 term are equal and the xy term is zero.

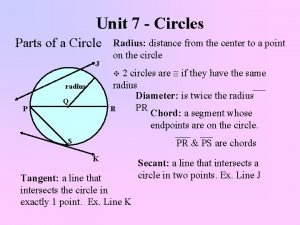
Tangent to the circle. Let A be a fixed point on the circumference of circle O and P be another variable point on the circumference. As P approaches A along the circumference, the chord AP will rotate about A. The limiting position AT of the variable chord AP is called the tangent to the circle O at the point A and A is the point of contact.

In other words, a line that intersects the circle in exactly one point is said to be tangent to the circle. Equation of the tangent to the circle x 2 + y 2 + Dx + Ey + F = 0 at the point P(x 1, y 1)

slope = m The equations of the two tangents with slope m to the circle x 2 + y 2 = r 2 are

Condition for tangency A straight line y = mx + c is a tangent to the circle x 2 + y 2 = r 2 if and only if c 2 = r 2( 1 + m 2).

Length of the tangent from the point P(x 1, y 1) to the circle x 2 + y 2 + Dx + Ey + F = 0 is (x 1, y 1)

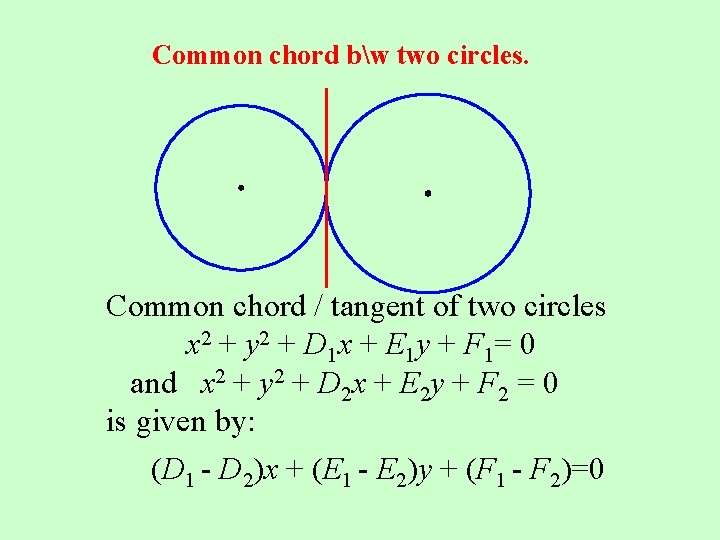
Common chord bw two circles. Common chord / tangent of two circles x 2 + y 2 + D 1 x + E 1 y + F 1= 0 and x 2 + y 2 + D 2 x + E 2 y + F 2 = 0 is given by: (D 1 - D 2)x + (E 1 - E 2)y + (F 1 - F 2)=0

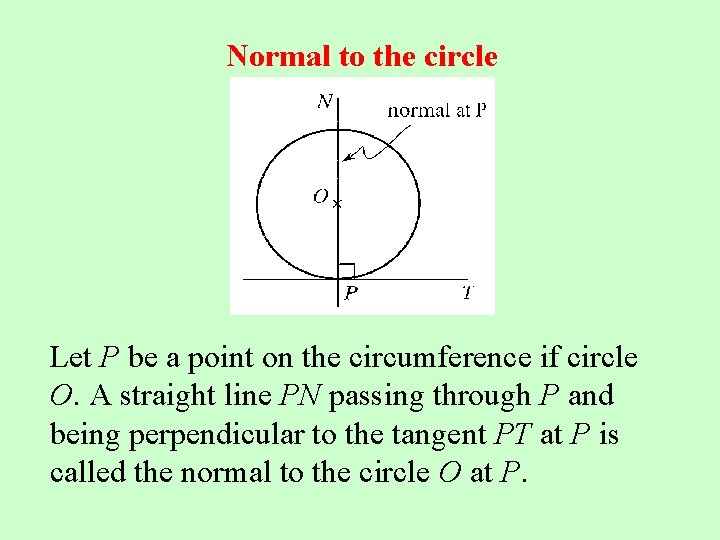
Normal to the circle Let P be a point on the circumference if circle O. A straight line PN passing through P and being perpendicular to the tangent PT at P is called the normal to the circle O at P.

The equations of the normal to the circle x 2 + y 2 + Dx + Ey + F = 0 at the point P(x 1, y 1) is P(x 1, y 1)

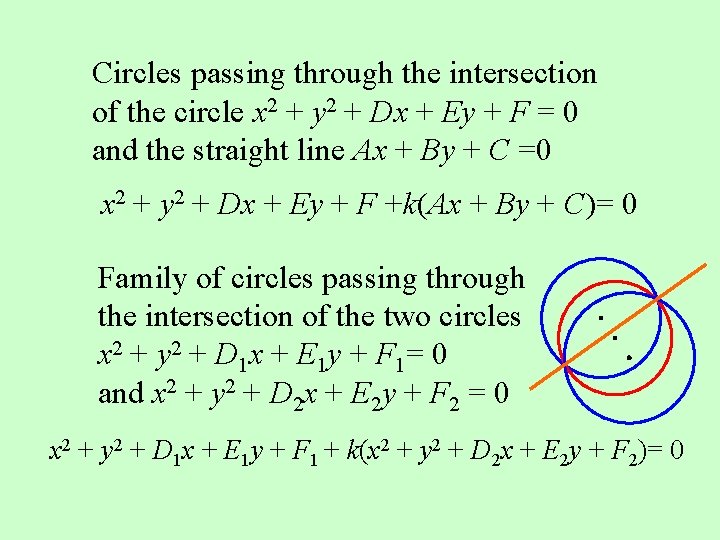
Circles passing through the intersection of the circle x 2 + y 2 + Dx + Ey + F = 0 and the straight line Ax + By + C =0 x 2 + y 2 + Dx + Ey + F +k(Ax + By + C)= 0 Family of circles passing through the intersection of the two circles x 2 + y 2 + D 1 x + E 1 y + F 1= 0 and x 2 + y 2 + D 2 x + E 2 y + F 2 = 0 x 2 + y 2 + D 1 x + E 1 y + F 1 + k(x 2 + y 2 + D 2 x + E 2 y + F 2)= 0

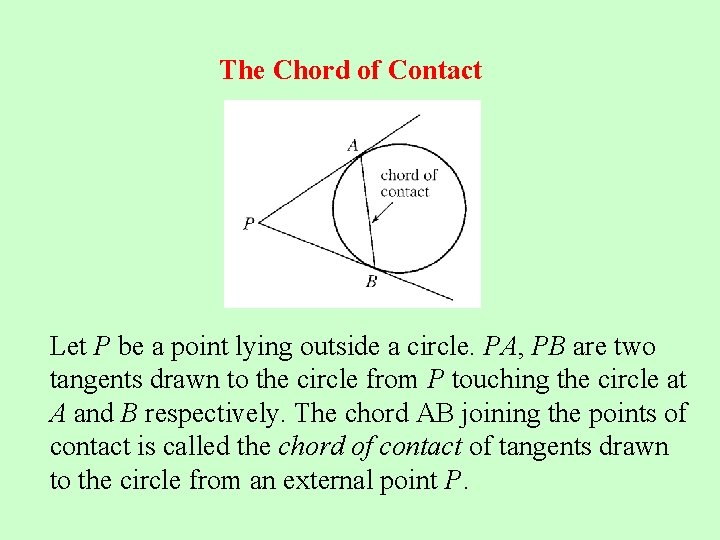
The Chord of Contact Let P be a point lying outside a circle. PA, PB are two tangents drawn to the circle from P touching the circle at A and B respectively. The chord AB joining the points of contact is called the chord of contact of tangents drawn to the circle from an external point P.

Equation of the Chord of Contact Let P(x 1, y 1) be a point lying outside the circle x 2 + y 2 + Dx + Ey + F = 0. Then the equation


The sphere appears in nature whenever a surface wants to be as small as possible. Examples include bubbles and water drops. Some special spheres in nature are

A sphere is defined as the set of all points in threedimensional space that are located at a distance r (the "radius") from a given point (the "center"). Equation of the sphere with center at the origin (0, 0, 0) and radius R is given by The Cartesian equation of a sphere centered at the point (x 0, y 0, z 0) with radius R is given by

GREAT CIRCLE A great circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as distinct from a small circle. Any diameter of any great circle coincides with a diameter of the sphere, and therefore all great circles have the same circumference as each other, and have the same center as the sphere. A great circle is the largest circle that can be drawn on any given sphere. Every circle in Euclidean space is a great circle of exactly one sphere.

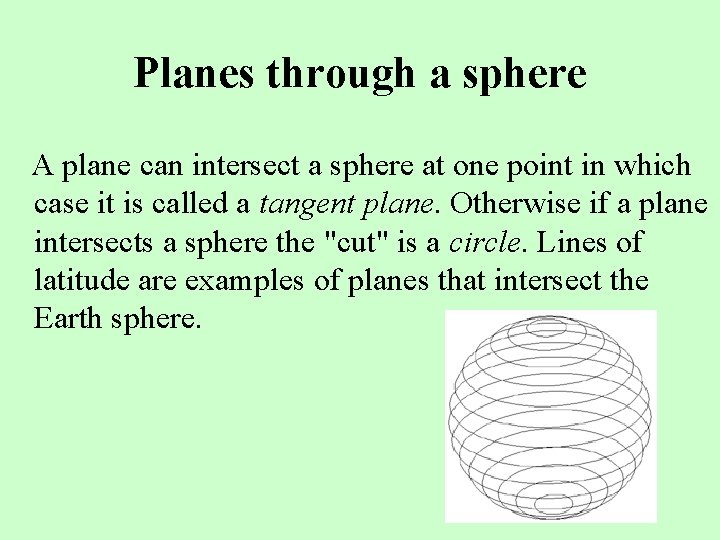
Planes through a sphere A plane can intersect a sphere at one point in which case it is called a tangent plane. Otherwise if a plane intersects a sphere the "cut" is a circle. Lines of latitude are examples of planes that intersect the Earth sphere.

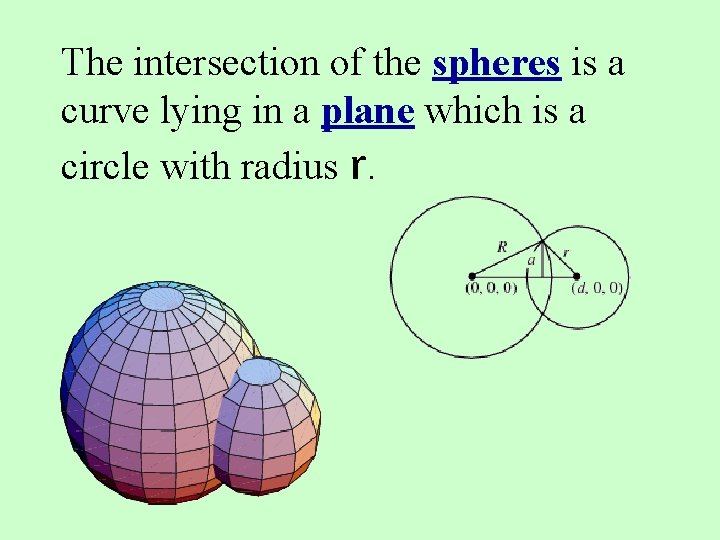
The intersection of the spheres is a curve lying in a plane which is a circle with radius r.

Sphere Facts ØIt is perfectly symmetrical ØIt has no edges or vertices (corners) ØIt is not a polyhedron ØAll points on the surface are the same distance from the center

 Difference between structural and geometric isomers
Difference between structural and geometric isomers Engineering drawing symbols and meanings
Engineering drawing symbols and meanings Geometric tolerance
Geometric tolerance Tolerancing
Tolerancing Geometrical optics ppt
Geometrical optics ppt Geometrical
Geometrical Geometrical
Geometrical Geographical data types
Geographical data types Geometrical representation of complex number
Geometrical representation of complex number Lateral area of cylinder
Lateral area of cylinder Geometrical spreading
Geometrical spreading Geometrical shadow
Geometrical shadow Geometrical isomerism
Geometrical isomerism Vertical
Vertical What is the point of tangency in circle j?
What is the point of tangency in circle j? Open circle on a number line
Open circle on a number line Geometry circles
Geometry circles Interpreting circle graphs
Interpreting circle graphs How do you find circumference
How do you find circumference Definition of a tangent of a circle
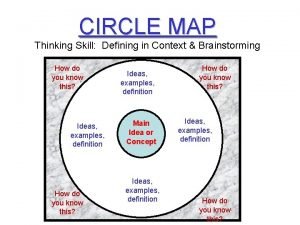
Definition of a tangent of a circle Circle map definition
Circle map definition Defining in context circle map
Defining in context circle map Involute of a circle
Involute of a circle Athlete’s circle of care
Athlete’s circle of care Vocabulary circle map
Vocabulary circle map