Minimizing DFAs CS 154 Omer Reingold Does this

Minimizing DFAs CS 154, Omer Reingold

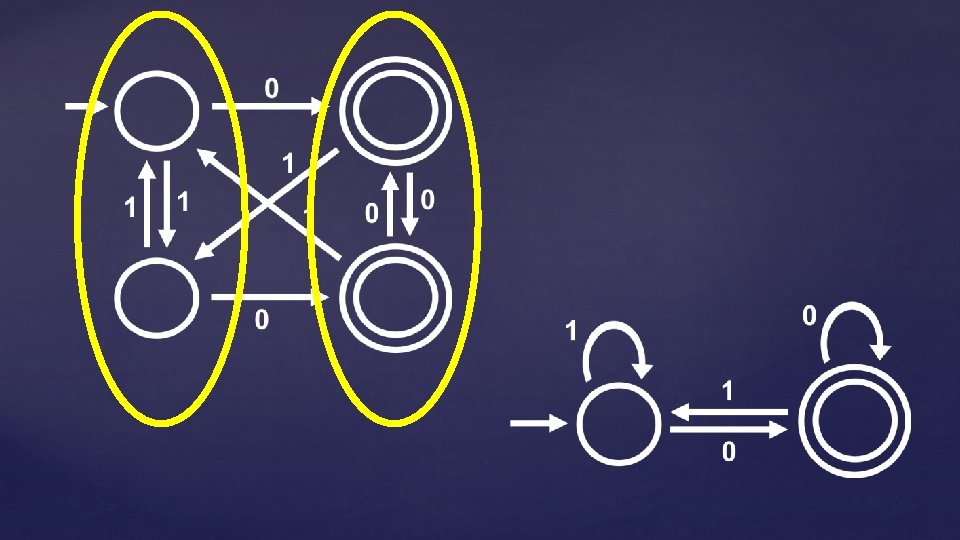
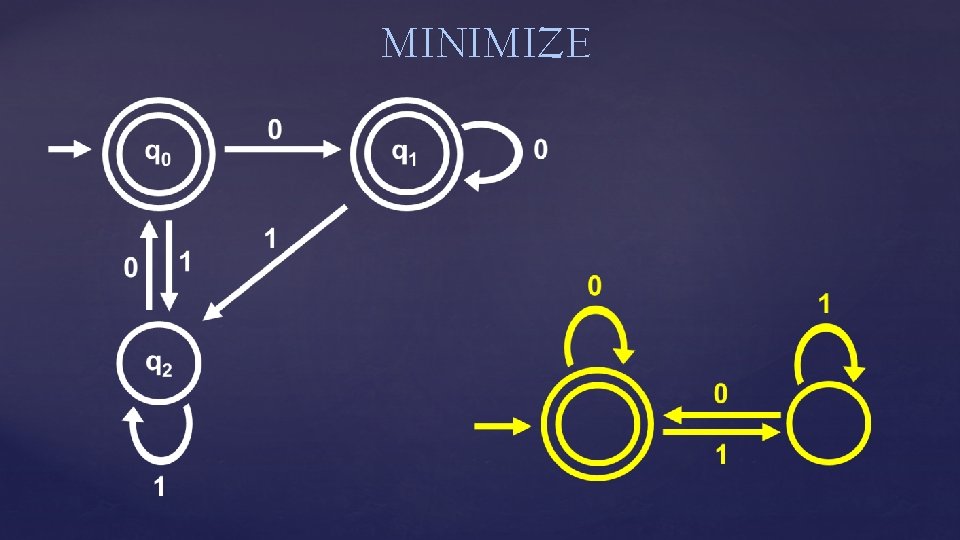
Does this DFA have a minimal number of states?

Is this minimal? How can we tell in general?

Theorem: For every regular language L, there is a unique (up to re-labeling of the states) minimal-state DFA M* such that L = L(M*). Furthermore, there is an efficient algorithm will output this unique M*. which, given any DFA M, If these were true for more general models of computation, that would be an engineering breakthrough

Note: There isn’t a uniquely minimal NFA

Extending transition function to strings Given DFA M = (Q, Σ, , q 0, F), we extend to a function : Q Σ* → Q as follows: (q, ε) = q (q, ) = (q, ) (q, 1 … k+1 ) = ( (q, 1 … k ), k+1 ) (q, w) = the state of M reached after reading in w, starting from state q Note: (q 0, w) F M accepts w Def. w Σ* distinguishes states q 1 and q 2 if exactly (q (q (q 1, w)one Fof (q 2 F, w) is a final state 1, w), 2, w)

Distinguishing two states Def. w Σ* distinguishes states q 1 and q 2 if exactly one of (q 1, w), (q 2, w) is a final state I’m in q 1 or q 2, but which? How can I tell? Ok, I’m accepting ! Must have been q 1 Here… read this W

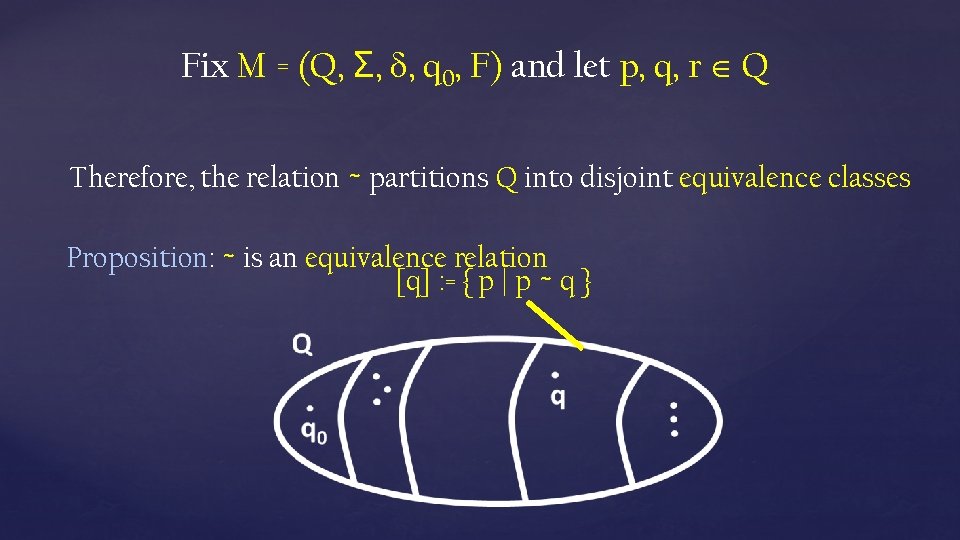
Fix M = (Q, Σ, , q 0, F) and let p, q Q Definitions: State p is distinguishable from state q if there is w Σ* that distinguishes p and q ( there is w Σ* so that exactly one of (p, w), (q, w) is a final state) State p is indistinguishable from state q if p is not distinguishable from q ( for all w Σ*, (p, w) F (q, w) F) Pairs of indistinguishable states are redundant…

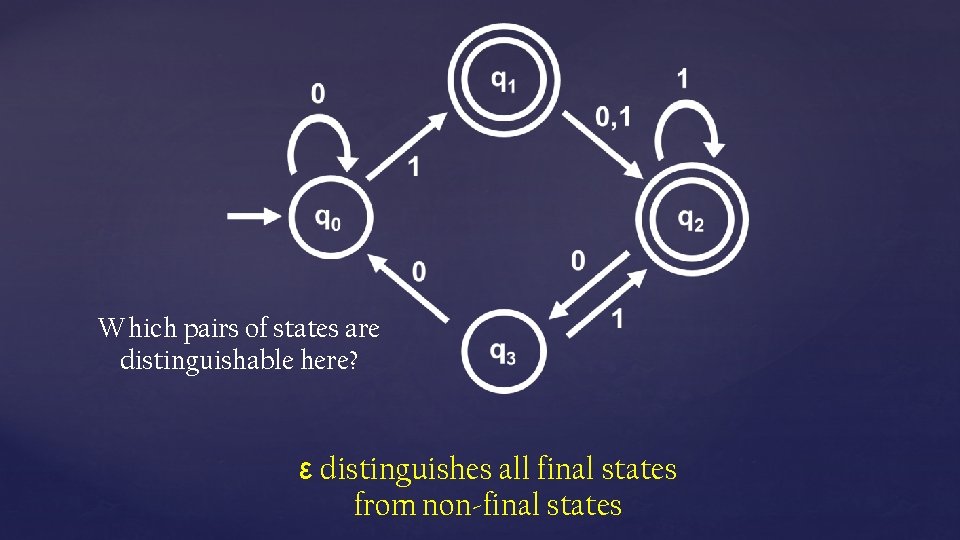
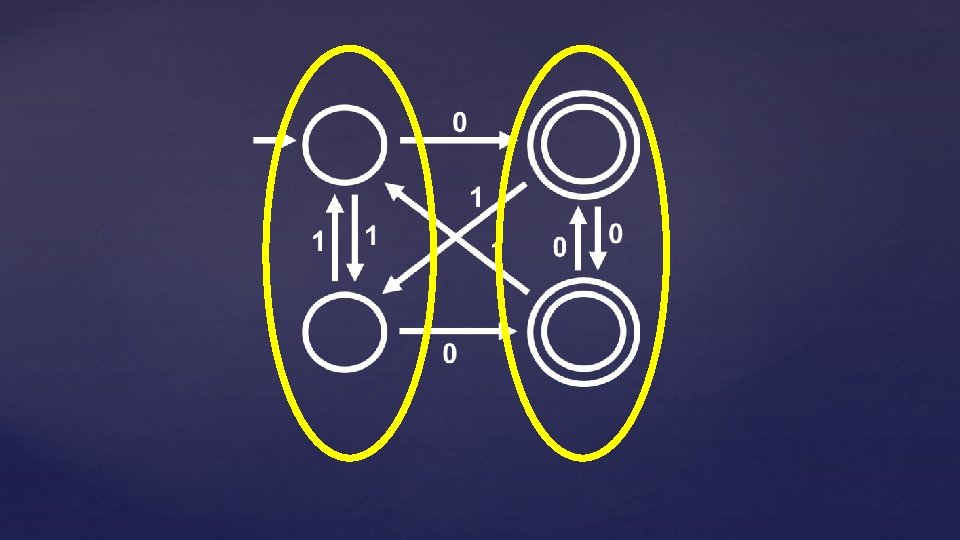
Which pairs of states are distinguishable here? ε distinguishes all final states from non-final states

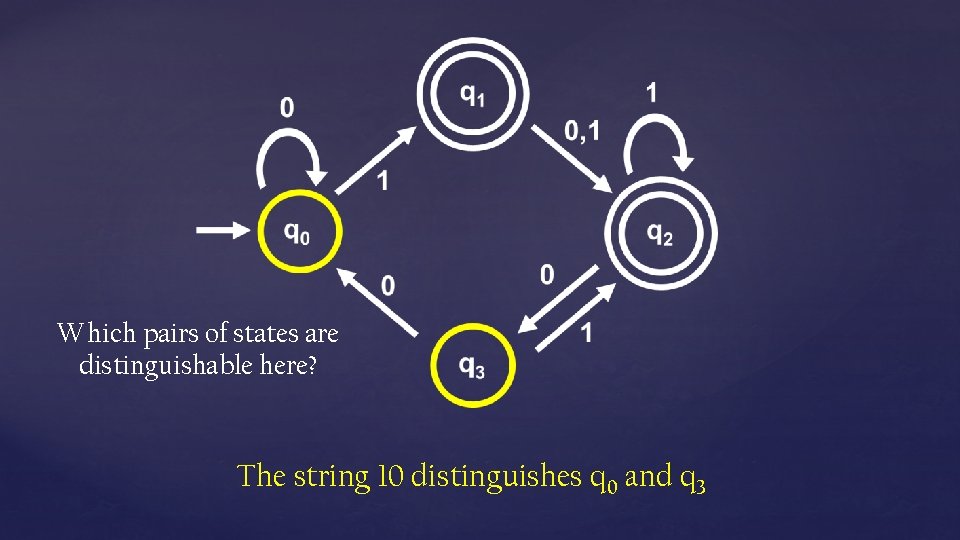
Which pairs of states are distinguishable here? The string 10 distinguishes q 0 and q 3

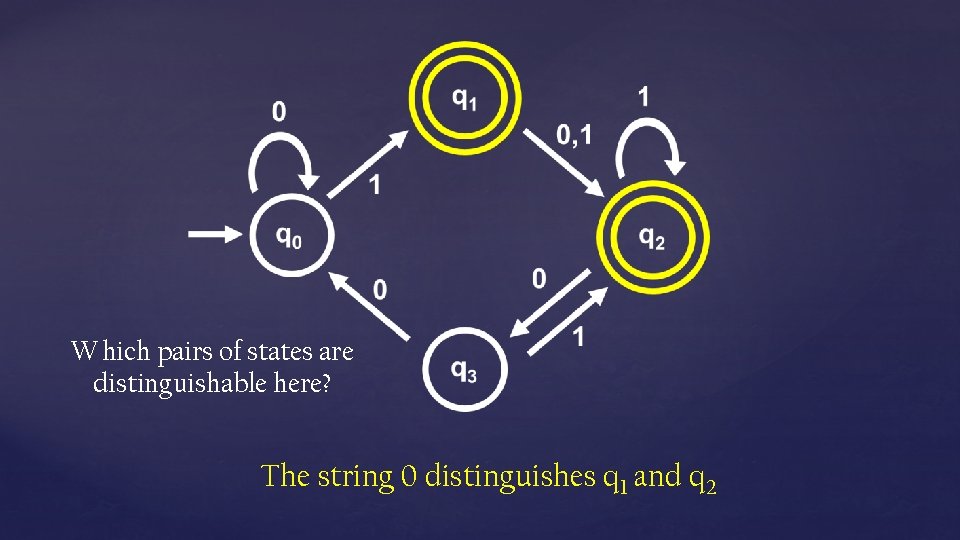
Which pairs of states are distinguishable here? The string 0 distinguishes q 1 and q 2

Fix M = (Q, Σ, , q 0, F) and let p, q, r Q Define a binary relation ∼ on the states of M: p ∼ q iff p is indistinguishable from q p ≁ q iff p is distinguishable from q Proposition: ∼ is an equivalence relation p ∼ p (reflexive) p ∼ q q ∼ p (symmetric) p ∼ q and q ∼ r p ∼ r (transitive) Proof?

Fix M = (Q, Σ, , q 0, F) and let p, q, r Q Therefore, the relation ∼ partitions Q into disjoint equivalence classes Proposition: ∼ is an equivalence relation [q] : = { p | p ∼ q }

Algorithm: MINIMIZE-DFA Input: DFA M Output: DFA MMIN such that: L(M) = L(MMIN) MMIN has no inaccessible states MMIN is irreducible || For all states p q of MMIN, p and q are distinguishable Theorem: MMIN is the unique minimal DFA that is equivalent to M

Intuition: The states of MMIN will be the equivalence classes of states of M We’ll uncover these equivalent states with a dynamic programming algorithm

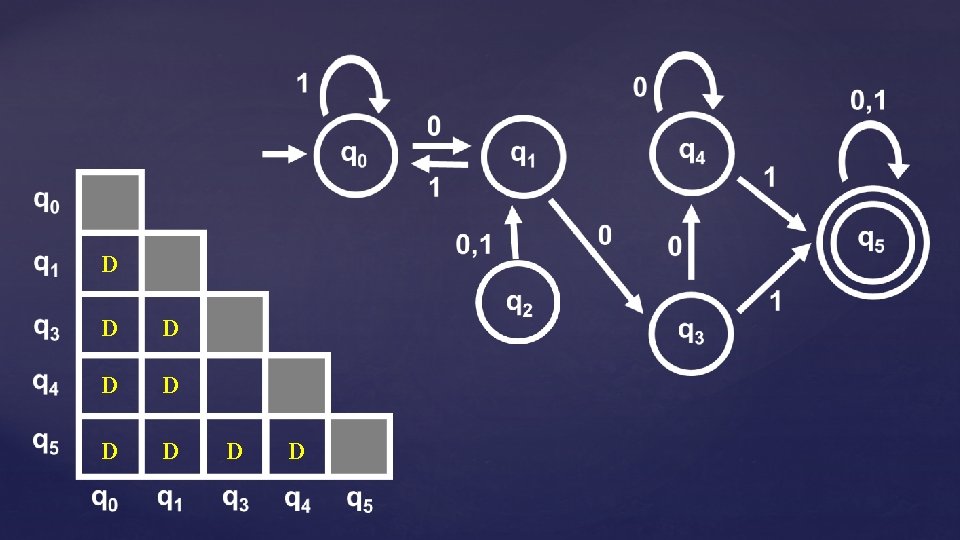
The Table-Filling Algorithm Input: DFA M = (Q, Σ, , q 0, F) Output: (1) DM = { (p, q) | p, q Q and p ≁ q } (2) EQUIVM = { [q] | q Q } High-Level Idea: • We know how to find those pairs of states that the string ε distinguishes… • Use this and iteration to find those pairs distinguishable with longer strings • The pairs of states left over will be indistinguishable

The Table-Filling Algorithm Input: DFA M = (Q, Σ, , q 0, F) Output: (1) DM = { (p, q) | p, q Q and p ≁ q } (2) EQUIVM = { [q] | q Q } Base Case: For all (p, q) such that p accepts and q rejects p ≁ q

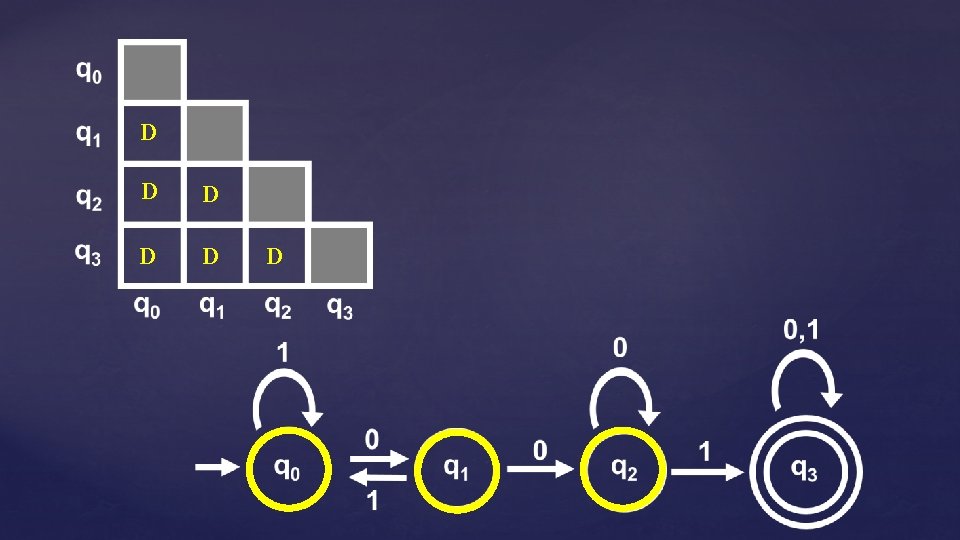
The Table-Filling Algorithm Input: DFA M = (Q, Σ, , q 0, F) Output: (1) DM = { (p, q) | p, q Q and p ≁ q } (2) EQUIVM = { [q] | q Q } Base Case: For all (p, q) such that p accepts and q rejects p ≁ q Iterate: If there are states p, q and symbol σ Σ satisfying: D D D (p, ) = p (q, ) = ≁ q mark p≁q Repeat until no more D’s can be added

D D D

D D D 22 D

Claim: If (p, q) is marked D by the Table-Filling algorithm, then p ≁ q Proof: By induction on the number of steps in the algorithm before (p, q) is marked D If (p, q) is marked D at the start , then one state’s in F and the other isn’t, so ε distinguishes p and q Suppose (p, q) is marked D at a later point. Then there are states p , q such that: 1. (p , q ) are marked D p ≁ q (by induction) So there’s a string w s. t. (p , w) F (q , w) F 2. p = (p, ) and q = (q, ), where Σ The string w distinguishes p and q!

Claim: If (p, q) is not marked D by the Table-Filling algorithm, then p ∼ q Proof (by contradiction): Suppose the pair (p, q) is not marked D by the algorithm, yet p ≁ q (call this a “bad pair”) Then there is a string w such that |w| > 0 and: (p, w) F and (q, w) F (Why is |w| > 0? ) Weallhave = w , forlet some w’ and Σ Of suchwbad pairs, p, qstring be a pair withsome the shortest distinguishing string w Let p = (p, ) and q = (q, ) Then (p , q ) is also a bad pair, but with a SHORTER distinguishing string, w !

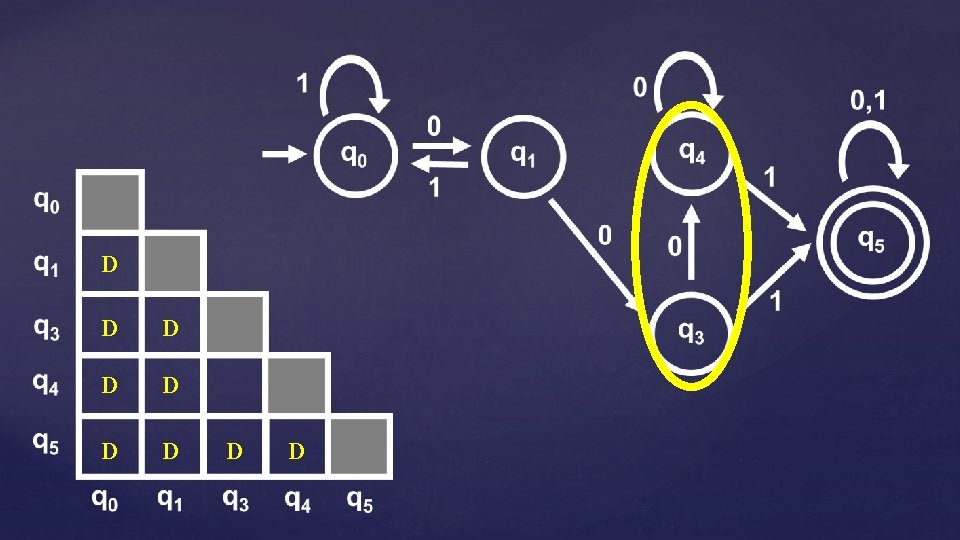
Algorithm MINIMIZE Input: DFA M Output: Equivalent minimal-state DFA MMIN 1. Remove all inaccessible states from M 2. Run Table-Filling algorithm on M to get: EQUIVM = { [q] | q is an accessible state of M } 3. Define: MMIN = (QMIN, Σ, MIN, q 0 MIN, FMIN) QMIN = EQUIVM, q 0 MIN = [q 0], FMIN = { [q] | q F } MIN( [q], ) = [ ( q, ) ] Claim: L(MMIN) = L(M)

MINIMIZE

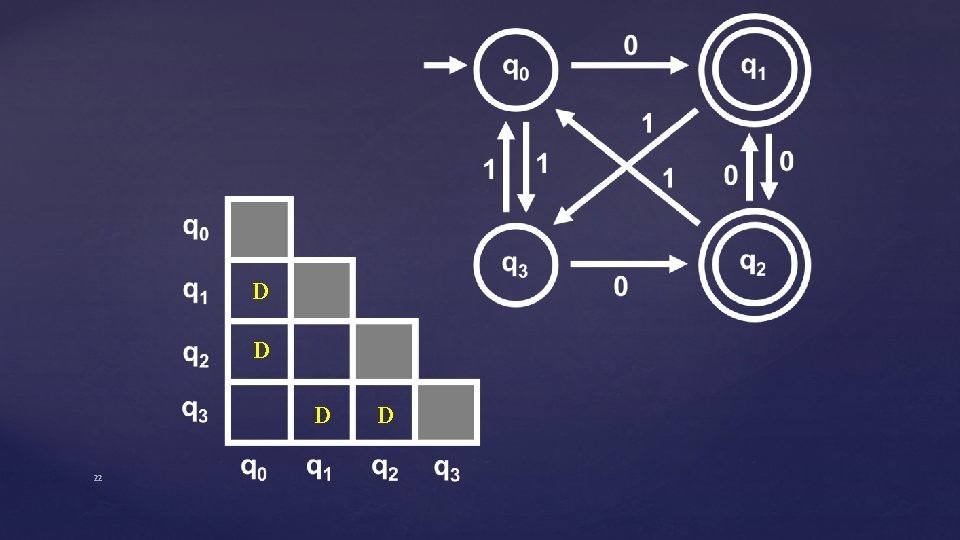
D D D D D

D D D D D

Thm: MMIN is the unique minimal DFA equivalent to M Claim: If L(M )=L(MMIN) and M has no inaccessible states and M’ is irreducible there is an isomorphism between M and MMIN Suppose for now the Claim is true. If M’ is a minimal DFA, then M’ has no inaccessible states and is irreducible (why? ) So the Claim implies: Let M’ be a minimal DFA for M. there is an isomorphism between output by MINIMIZE(M). The Thm holds! M’ and the DFA M MIN that is

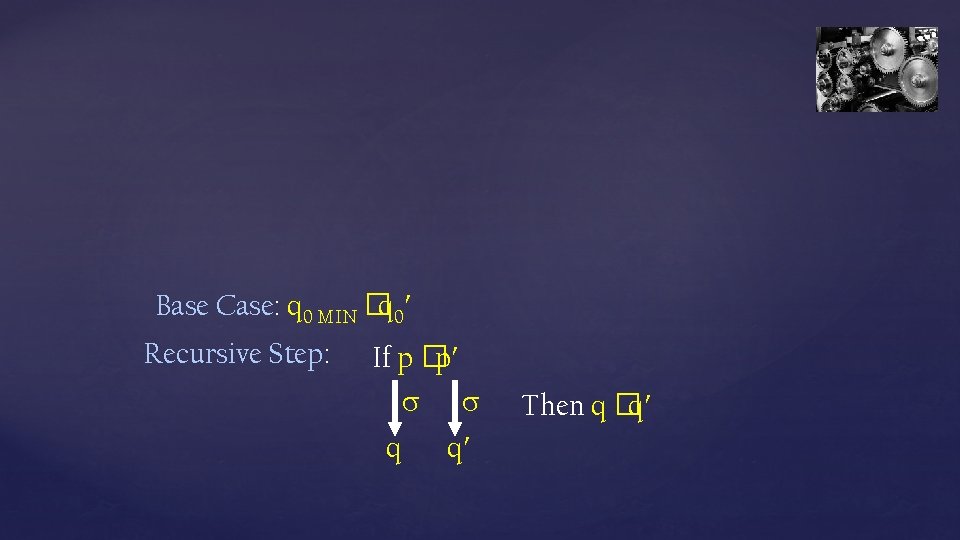
Thm: MMIN is the unique minimal DFA equivalent to M Claim: If L(M )=L(MMIN) and M has no inaccessible states and M’ is irreducible there is an isomorphism between M and MMIN Proof: We recursively construct a map from the states of MMIN to the states of M Base Case: q 0 MIN �q 0 Recursive Step: If p �p q q Then q �q

Base Case: q 0 MIN �q 0 Recursive Step: If p �p q q Then q �q

Base Case: q 0 MIN �q 0 Recursive Step: If p �p q Then q �q q We need to prove: The map is defined everywhere The map is well defined The map is a bijection The map preserves all transitions: If p �p then MIN(p, ) � ’(p’, ) (this follows from the definition of the map!)

Base Case: q 0 MIN �q 0 Recursive Step: If p �p q Then q �q q The map is defined everywhere That is, for all states q of MMIN there is a state q of M such that q �q If q MMIN, there is a string w such that MIN(q 0 MIN, w) = q Let q = (q 0 , w). Then q �q

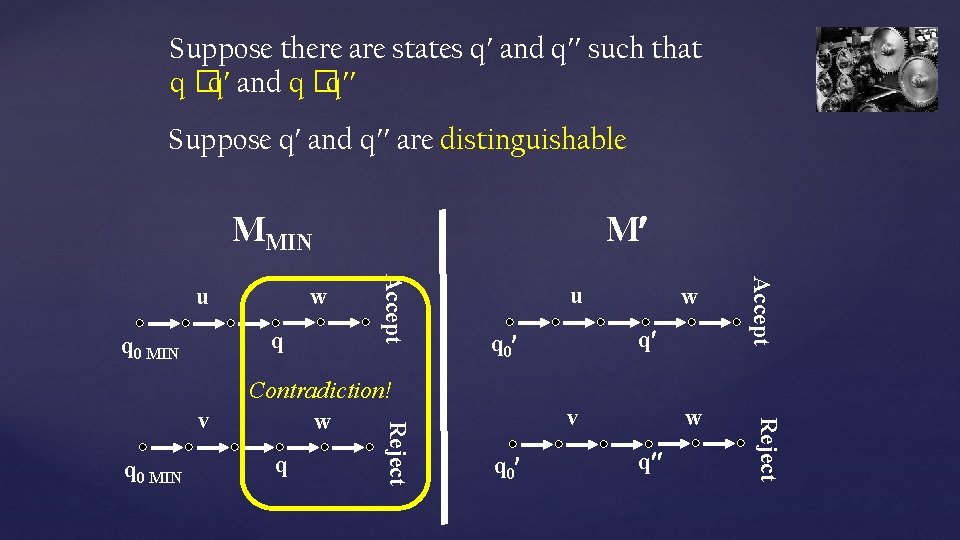
Base Case: q 0 MIN �q 0 Recursive Step: If p �p q Then q �q q The map is well defined Proof by contradiction. Suppose there are states q and q such that q �q and q �q We show that q and q are indistinguishable so it must be that q = q ,

Suppose there are states q and q such that q �q and q �q Suppose q and q are distinguishable MMIN v q 0 w q Reject q w q q 0 Contradiction! w Reject v u Accept q q 0 MIN w Accept u M

Base Case: q 0 MIN �q 0 Recursive Step: If p �p q Then q �q q The map is onto Want to show: For all states q of M there is a state q of MMIN such that q �q For every q there is a string w such that M’ reaches state q’ after reading in w Let q be the state of MMIN after reading in w Claim: q �q

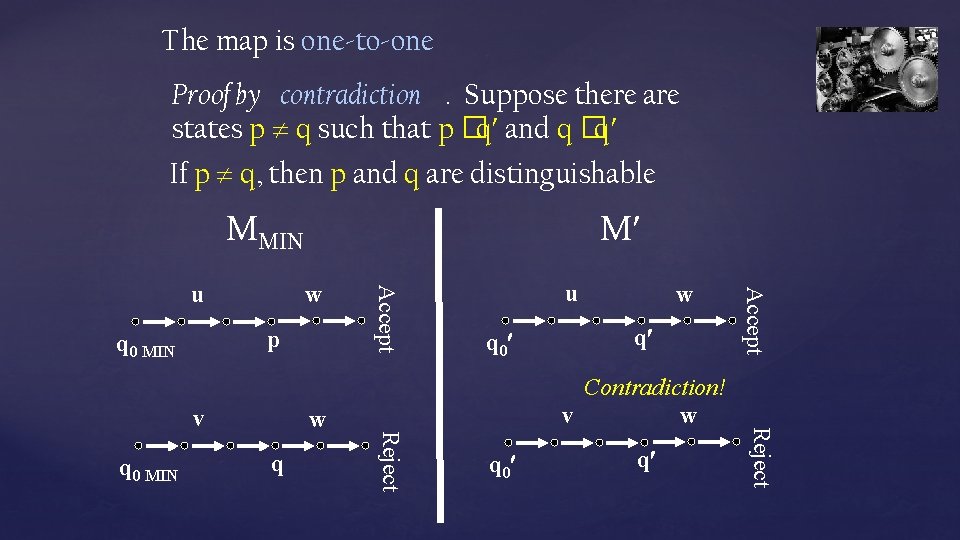
The map is one-to-one Proof by contradiction. Suppose there are states p q such that p �q and q �q If p q, then p and q are distinguishable MMIN p q 0 MIN q q q 0 q Reject q 0 MIN w q 0 w Contradiction! v w Reject v u Accept w Accept u M

How can we prove that two regular expressions are equivalent?

Parting thoughts: DFAs can be optimized Later: Can DFAs be learned?