1 Sebuah topi berbentuk kerucut mempunyai diameter alas

1. Sebuah topi berbentuk kerucut mempunyai diameter alas 14 cm, dan tinggi 24 cm. hitunglah volume luas topi! Diketahui : d = 14 cm r = = 7 cm t = 24 cm Ditanya : v dan l ? Penyelesaian : Volume = π r 2 t = x x 7 cm x 24 cm = 1232 cm 3 Luas = π rs + r 2 = S = = = = S = 25 cm = 22 x 7 cm x 25 cm + 22 x 7 cm 7 7 = 550 cm 2 + 154 cm 2 = 704 cm 2

2. Diketahui sebuah bandul berbentuk kerucut mempunyai volume = 37, 68 cm 3 dan tinggi = 4 cm. berapakah luas permukaan bandul ! Diketahui : v = 37, 68 cm 3 T = 4 cm Ditanya : L ? Penyelesaian : v = π r 2 t 37, 68 cm 3 = . 3. 14. r 2. 4 cm 37, 68 cm 3 x = 12, 5 cm. r 2 113, 04 cm 3 = 12, 56 cm. r 2 r 2 = 9 cm 2` r = 3 cm s = s = 5 cm L = π rs + π r 2 = 3, 14 x 3 cm x 5 cm + 3, 14 x 3 cm = 47, 1 cm 2 + 28, 26 cm 2 = 75, 36 cm 2

3. Diketahui luas alas sebuah kerucut adalah 113, 04 cm 2 dan panjang sisi miring 10 cm. berapakah luas seluruh permukaan kerucut dan hitung pula volumenya! Diketahui : L alas = 113, 04 cm 2 S = 10 cm Di Tanya : L permukaan kerucu dan volumenya? Penyelesaian : L alas = π r 2 113, 04 cm 2 = 3, 14 r 2 r 2 = 36 cm 2 r = 6 cm t = t = 8 cm L. kerucut = π r s + π r 2 = 3, 14 x 6 cm x 10 cm x 3, 14 x 6 cm = 188, 4 cm 2 + 113, 04 cm 2 = 301, 44 cm 2 V. kerucut = π r 2 t = 3, 14 x 6 cm x 8 cm = 301, 44 cm 3

4. Sebuah kerucut mempunyai keliling alas 62, 8 cm. jika tinggi kerucut sama denga panjang jari-jarinya berapa volume kerucut ? Diketahui : K. alas = 62, 8 cm T=r Ditanya : v. kerucut ? Penyelesaian : k. alas = π. d 62, 8 cm = 3, 14. d d= d = 20 cm r= . d r= . 20 r = 10 t=r t = 10 v= π. . t =. 3, 14 x 10 cm =. 3140 cm 3 = 1046, 67 cm 3

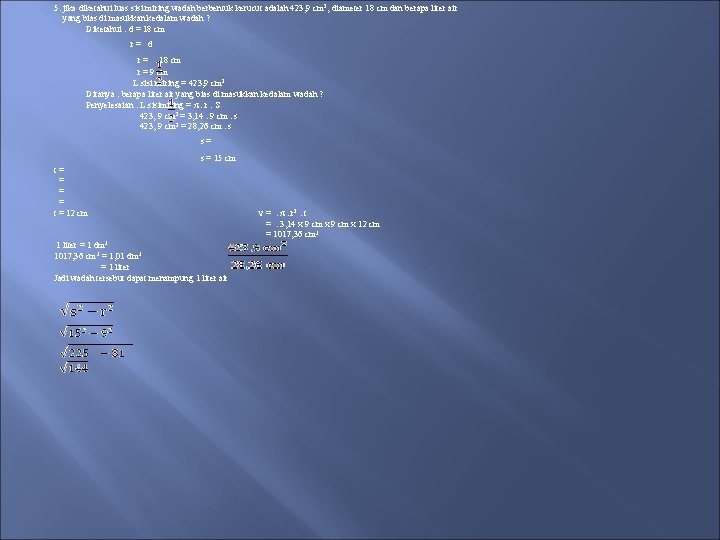
5. jika diketahui luas sisi miring wadah berbentuk kerucut adalah 423, 9 cm 2, diameter 18 cm dan berapa liter air yang bias di masukkan kedalam wadah ? Diketahui : d = 18 cm r = d r = . 18 cm r = 9 cm L. sisi miring = 423, 9 cm 2 Ditanya : berapa liter air yang bias di masukkan kedalam wadah ? Penyelesaian : L. sisimiring = π. r. S 423, 9 cm 2 = 3, 14. 9 cm. s 423, 9 cm 2 = 28, 26 cm. s s = 15 cm t = = = = t = 12 cm 1 liter = 1 dm 3 1017, 36 cm 3 = 1, 01 dm 3 = 1 liter Jadi wadah tersebut dapat menampung 1 liter air v = . π. r 2. t = . 3, 14 x 9 cm x 12 cm = 1017, 36 cm 3