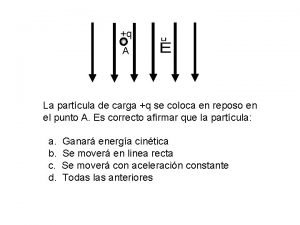
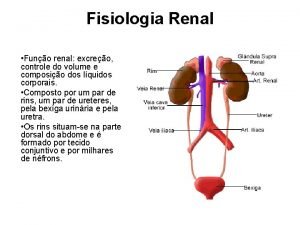
Mecnica Quntica Funo de Onda q Partcula meio

Mecânica Quântica: Função de Onda q Partícula: meio partícula…meio onda… Teorema de Fourier: representar a partícula como uma superposição de muitas ondas. Somando quantidades variáveis de um infinito número de ondas Função de onda do elétron Amplitude da onda com número de onda k=2 p/l Expressão senoidal para harmônicos

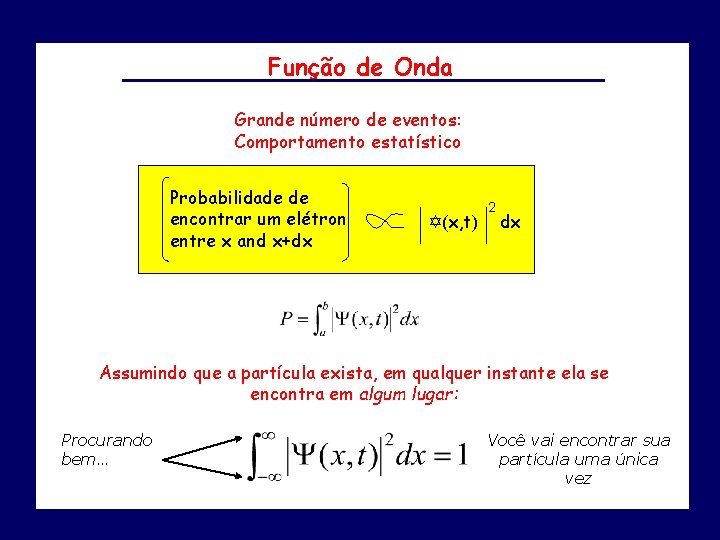
Função de Onda Grande número de eventos: Comportamento estatístico Probabilidade de encontrar um elétron entre x and x+dx Y(x, t) 2 dx Assumindo que a partícula exista, em qualquer instante ela se encontra em algum lugar: Procurando bem… Você vai encontrar sua partícula uma única vez

Função de Onda q Função clássica típica para uma partícula que se propaga na direção +x: q Analogamente, para a partícula que se propaga na direção –x: q Sabemos ainda que se 1 e 2 são ambas permitidas, 1 + 2 também será (Princípio da superposição) partícula desaparece para múltiplos inteiros de p/2, 2 p/3, etc.

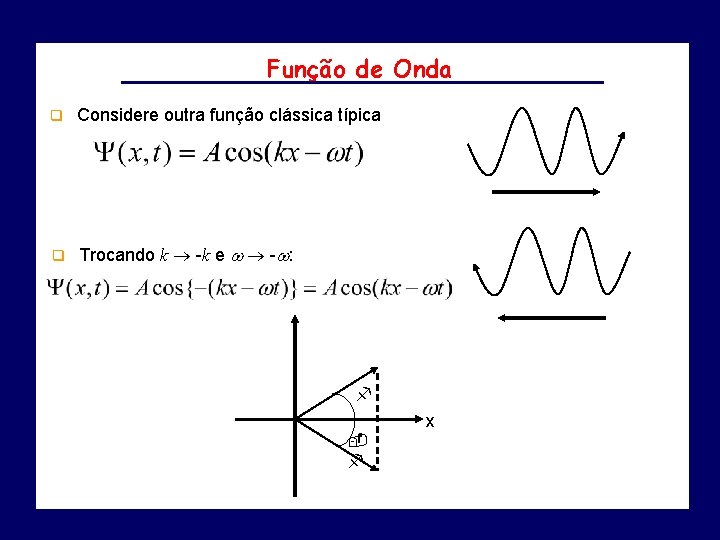
Função de Onda q Considere outra função clássica típica q Trocando k -k e - : f x f

Função de Onda Representação gráfica de um número complexo z como um ponto no plano complexo. q As componentes horizontal e vertical representam as partes real e imaginária respectivamente. q

Função de Onda q Partícula: meio partícula…meio onda… A partícula quântica é descrita por uma função de onda (r, t), que: § Contém toda a informação sobre a dinâmica da partícula § É uma função complexa § É unívoca, finita e contínua § Tem derivadas unívocas, finitas e contínuas

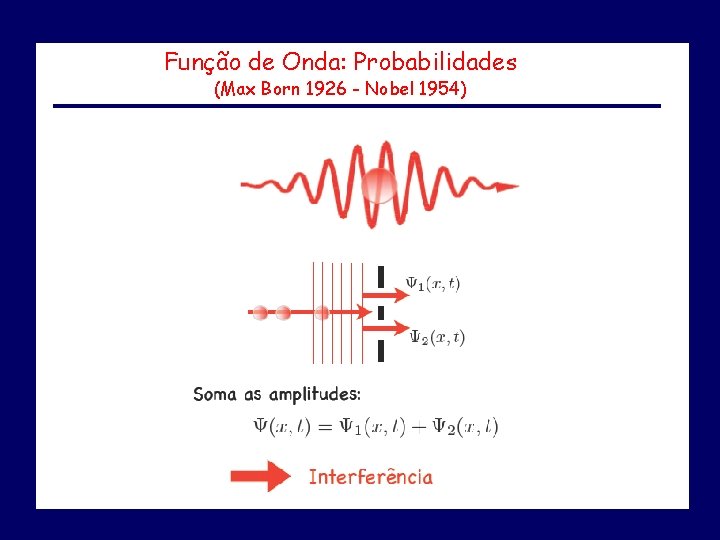
Função de Onda: Probabilidades (Max Born 1926 - Nobel 1954) Se, no instante t, é feita uma medida da localização da partícula associada à função de onda (x, t), então a probabilidade P (x, t)dx de que a partícula seja encontrada entre x e x+dx é igual a *(x, t)dx. Note que P (x, t) é real e não-negativa, como toda probabilidade… “Deus não joga dados com o universo” “Einstein, pare de dizer a Deus o que fazer” (A. Einstein) (Niels Bohr)

Função de Onda: Probabilidades (Max Born 1926 - Nobel 1954)

A Equação de Schrödinger (Nobel 1933) V(x, t): energia potencial e, se V(x) Eq. Schrödinger independente do tempo:

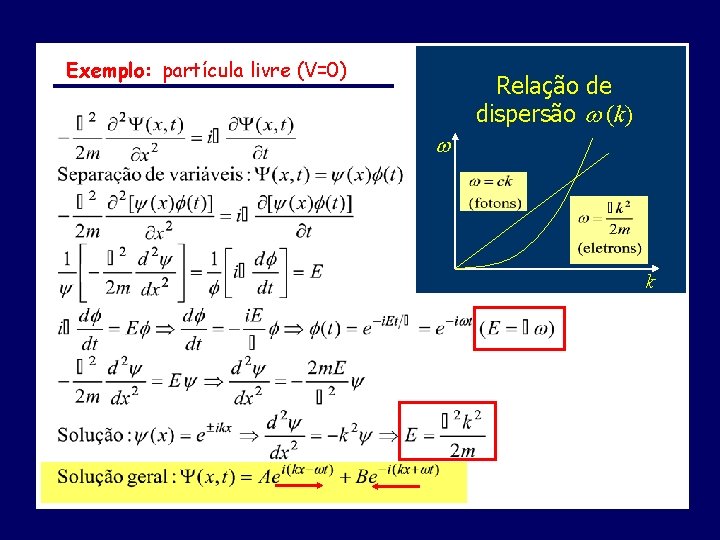
Exemplo: partícula livre (V=0) Relação de dispersão (k) k

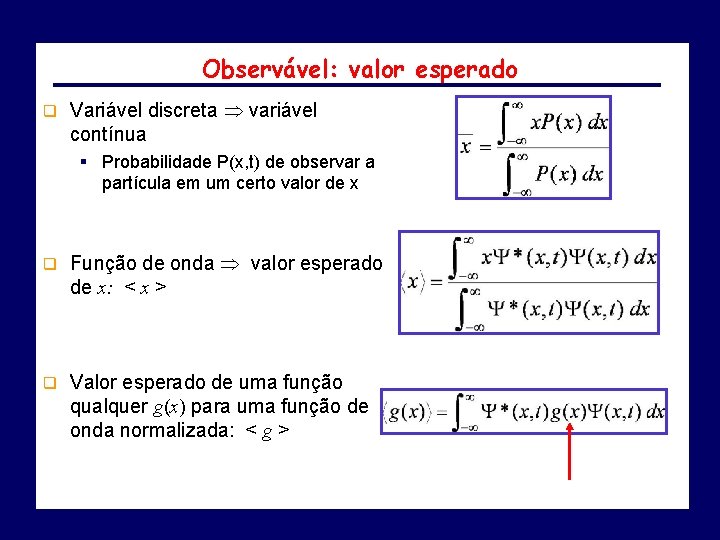
Observável: valor esperado q Valor esperado: resultado que se espera encontrar para a média de muitas medidas de uma certa quantidade. q Observável: qualquer quantidade mensurável para a qual podemos calcular o valor esperado (posição, momento, energia…) q Valor esperado de um observável: REAL q Valor médio de uma variável discreta x: 3 3 4 4

Observável: valor esperado q Variável discreta variável contínua § Probabilidade P(x, t) de observar a partícula em um certo valor de x q Função de onda valor esperado de x: < x > q Valor esperado de uma função qualquer g(x) para uma função de onda normalizada: < g >

Valor esperado e Operadores q Valor esperado do momento: necessário representar o momento p como função de x e t. Considere a derivada da função de onda de uma partícula livre (V=0) com respeito à x: q Logo: q Podemos associar ao momento um operador: q Valor esperado de p:

Valor esperado e Operadores: Posição e Energia A posiçao x é seu próprio operador. q Considere a derivada temporal da função de onda de uma partícula livre: q q Logo: q Podemos associar à energia um operador: q Valor esperado de E :

Operadores A cada grandeza física corresponde um operador matemático, que opera na função de onda. Energia cinética + potencial = energia cinética o potencial energia total posição x momento p energia potencial V energia cinética K energia total E x V(x) operador observável q

Operadores, autofunção e autovalor Quando aplicamos um operador a e obtemos de volta a própria multiplicada por uma constante, diz-se que é uma autofunção do operador, com autovalor igual à constante obtida. q Quando isso acontece, diz-se que a grandeza física associada tem valor bem definido, com incerteza nula. q Assim, a da partícula livre é uma autofunção do operador momento, com autovalor ħk. q

Operadores, autofunção e autovalor A da partícula livre também é uma autofunção do operador energia, com autovalor ħ.

Operadores e a Eq. Schrödinger expressão para energia cinética o potencial Energia cinética + potencial = energia total

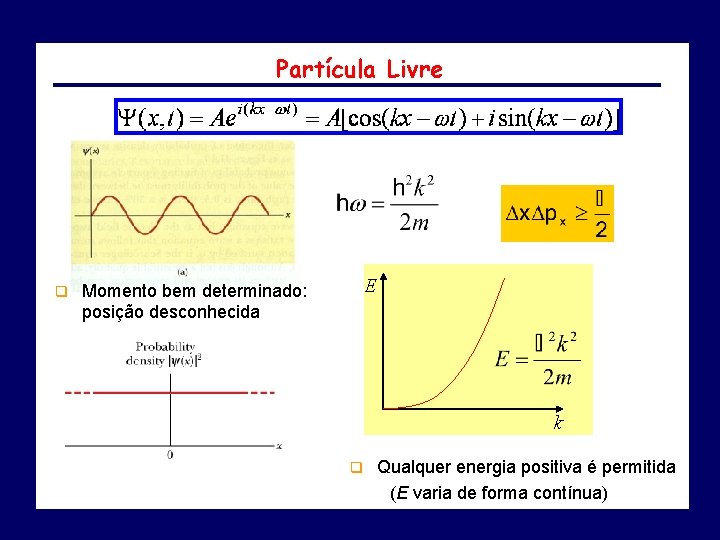
Partícula Livre q E Momento bem determinado: posição desconhecida k q Qualquer energia positiva é permitida (E varia de forma contínua)

Partícula na Caixa: Poço de potencial infinito V Região proibida 0 L x

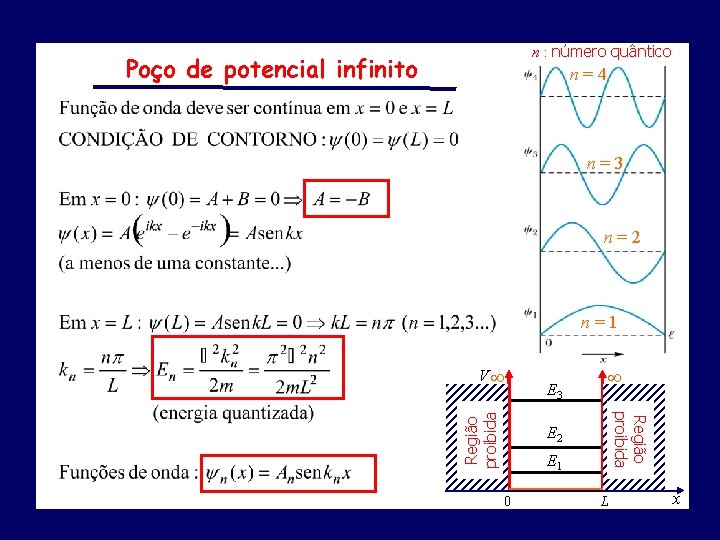
n : número quântico Poço de potencial infinito n=4 n=3 n=2 n=1 E 3 Região proibida V E 2 E 1 0 L x

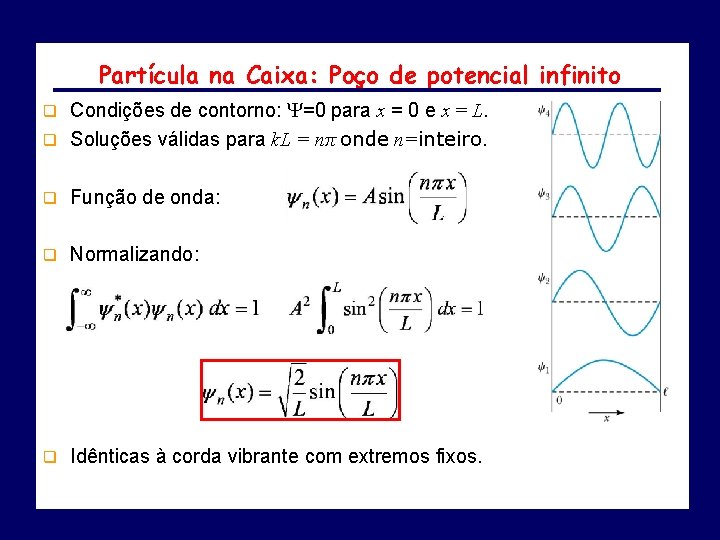
Partícula na Caixa: Poço de potencial infinito Condições de contorno: =0 para x = 0 e x = L. q Soluções válidas para k. L = nπ onde n=inteiro. q q Função de onda: q Normalizando: q Idênticas à corda vibrante com extremos fixos.

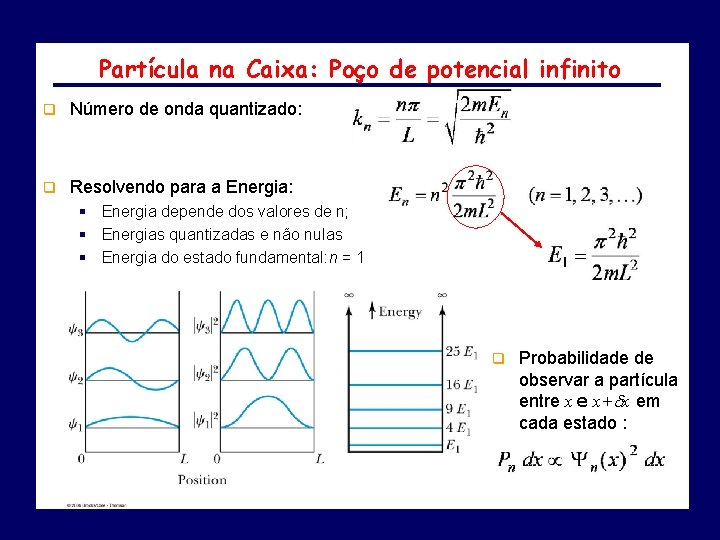
Partícula na Caixa: Poço de potencial infinito q Número de onda quantizado: q Resolvendo para a Energia: § Energia depende dos valores de n; § Energias quantizadas e não nulas § Energia do estado fundamental: n = 1 q Probabilidade de observar a partícula entre x e x+ x em cada estado :

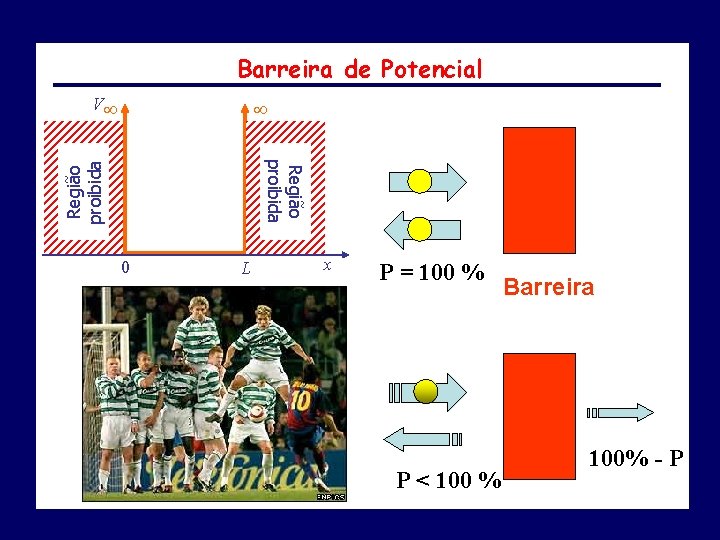
Barreira de Potencial V Região proibida 0 L x P = 100 % P < 100 % Barreira 100% - P

Potencial degrau V V 0 E < V 0 E 1 2 0 x

Encontrar B, C e D em termos de A q Função de onda e suas derivadas: § Finitas § Contínuas

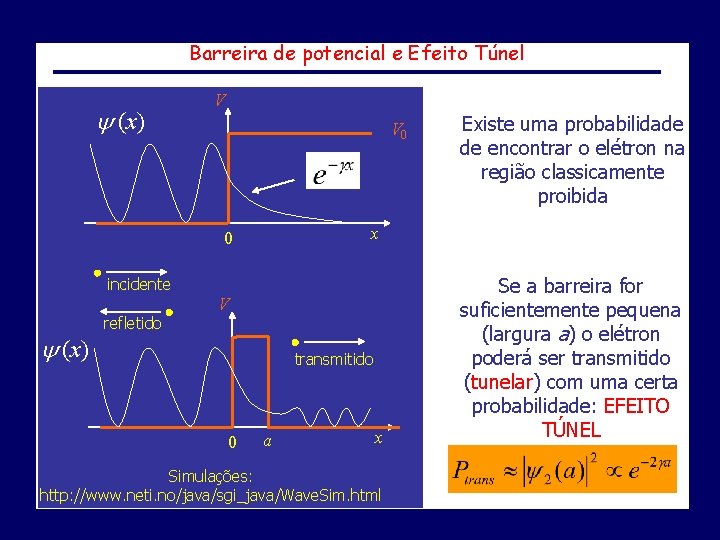
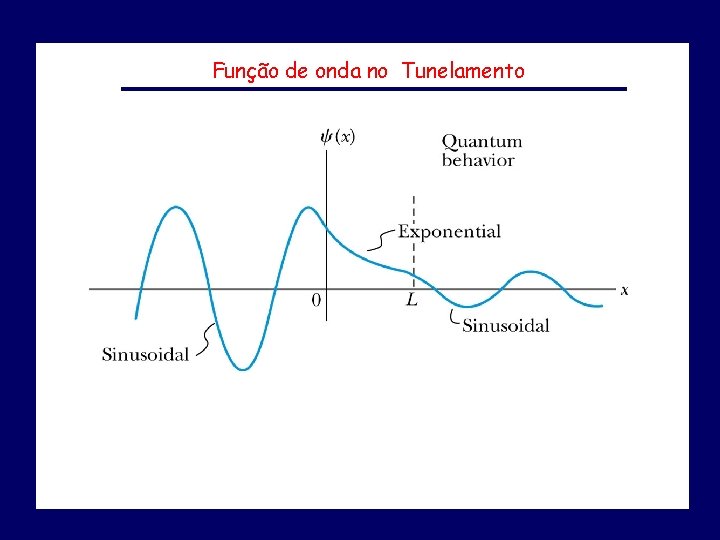
Barreira de potencial e Efeito Túnel (x) V V 0 x 0 incidente (x) refletido V transmitido 0 Existe uma probabilidade de encontrar o elétron na região classicamente proibida a x Simulações: http: //www. neti. no/java/sgi_java/Wave. Sim. html Se a barreira for suficientemente pequena (largura a) o elétron poderá ser transmitido (tunelar) com uma certa probabilidade: EFEITO TÚNEL

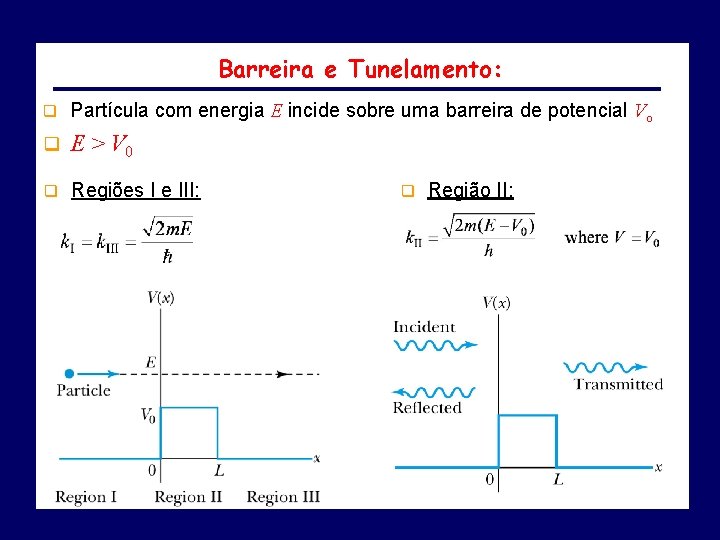
Barreira e Tunelamento: q Partícula com energia E incide sobre uma barreira de potencial Vo q E > V 0 q Regiões I e III: q Região II:

Barreira e Tunelamento: Onda incidente, refletida e transmitida: q Eq. Schrödinger nas 3 regiões: q q Soluções: q Onda se move para a direita:

Probabilidades de Reflexão e Transmissão q Probabilidade de reflexão R ou transmissão T : q R + T = 1. q Aplicando condições de contorno: x → ±∞, x = 0 e x = L q T pode ser = 1.

Tunelamento q E < V 0 q Classicamente a partícula não possui energia para vence a barreira q Existe probabilidade finita da partícula penetrar na barreira e aparecer do outro lado! q Probabilidade de transmissão descreve o fenômeno de tunelamento

Função de onda no Tunelamento