Macroscopic Analysis of Circuits Microscopic treatment insight into

























- Slides: 25

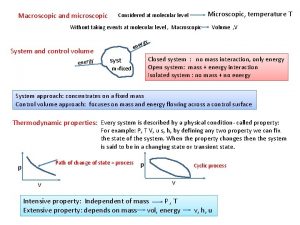
Macroscopic Analysis of Circuits Microscopic treatment: insight into the fundamental physical mechanism of circuit behavior. Not easy to measure directly E, u, Q, v. It is easier to measure conventional current, potential difference macroscopic parameters Need a link between microscopic and macroscopic quantities.

Resistance Many elements in a circuit act as resistors: prevent current from rising above a certain value. Goal: find a simple parameter which can predict V and I in such elements. Need to combine the properties of material and geometry.

Conductivity Combining the properties of a material Geometry Conventional current: Different properties of the material Group the material properties together: Current density: Conductivity

Exercise In copper at room temperature, the mobility of electrons is about 4. 5. 10 -3 (m/s)/(V/m) and the density of electrons is n=8. 1028 m-3. What is ? What is the strength of E required to drive a current of 0. 3 A through a copper wire which has a cross-section of 1 mm 2 ?

Exercise The conductivity of tungsten at RT is =1. 8. 107 (A/m 2)/(V/m) and it decreases 18 times at a temperature of a glowing filament (3000 K). The tungsten filament has a radius of 0. 015 mm. What is E required to dive 0. 3 A through it?

Conductivity with two Kinds of Charge Carriers

Resistance Conventional current: Widely known as Ohm’s law Resistance of a long wire: George Ohm (1789 -1854) Units: Ohm, Resistance combines conductivity and geometry!

Microscopic and Macroscopic View Microscopic Macroscopic Can we write V=IR ? Current flows in response to a V

Exercise: Carbon Resistor A = 0. 002 mm 2 Conductivity of Carbon: = 3. 104 (A/m 2)/(V/m) L=5 mm What is its resistance R? (V/A) What would be the current through this resistor if connected to a 1. 5 V battery?

Constant and Varying Conductivity Mobility of electrons: depends on temperature Conductivity and resistance depend on temperature.

Ohmic Resistors Ohmic resistor: resistor made of ohmic material… Ohmic materials: materials in which conductivity is independent of the amount of current flowing through not a function of current Examples of ohmic materials: metal, carbon (at constant T!)

Is a Light Bulb an Ohmic Resistor? Tungsten: mobility at room temperature is larger than at ‘glowing’ temperature (~3000 K) V-A dependence: 3 V 100 m. A 1. 5 V 80 m. A 0. 05 V 6 m. A Clearly not ohmic! R 30 19 8 I V

Semiconductors Metals, mobile electrons: slightest V produces current. If electrons were bound – we would need to apply some field to free some of them in order for current to flow. Metals do not behave like this! Semiconductors: n depends exponentially on E Conductivity rises (resistance drops) with rising temperature

Nonohmic Circuit Elements Semiconductors | V|=Q/C, function of time Capacitors Batteries: double current, but | V| emf, hardly changes has limited validity! Ohmic when R is indeppendent of I! Conventional symbols:

Series Resistance Vbatt + V 1 + V 2 + V 3 = 0 emf - R 1 I - R 2 I - R 3 I = 0 emf = R 1 I + R 2 I + R 3 I emf = (R 1 + R 2 + R 3) I emf = Requivalent I , where Requivalent = R 1 + R 2 + R 3

Exercise A certain ohmic resistor has a resistance of 40 . A second resistor is made of the same material, but is three times longer and has a half of the cross-sectional area. What is its resistance? Resistor 1: Resistor 2: What would be an equivalent resistance of these two resistors in series?

Exercise: Voltage Divider Know R , find V 1, 2 R 1 V 1 R 2 V 2 emf Solution: 1) Find current: 2) Find voltage: 3) Check:

Parallel Resistance I = I 1 + I 2 + I 3

Two Light Bulbs in Parallel R 1 = 30 R 2 = 10 What is the total current? Alternative way: What is the equivalent resistance?

Two Light Bulbs in Parallel What would you expect if one is unscrewed? A) The single bulb is brighter B) No difference C) The single bulb is dimmer

Work and Power in a Circuit Current: charges are moving work is done Work = change in electric potential energy of charges W= Power = work per unit time: I Power for any kind of circuit component: Units:

Example: Power of a Light Bulb I = 0. 3 A Units: emf = 3 V

Power Dissipated by a Resistor emf R Know V, find P Know I, find P In practice: need to know P to select right size resistor – capable of dissipating thermal energy created by current.

Energy Stored in a Capacitor Alternative approach: Energy density: Energy:

Real Batteries: Internal Resistance ideal battery Model of a real battery Round trip (energy conservation): rint 0. 25 1. 5 V R 100 1 0 R Ideal 0. 015 A 0. 15 A 1. 5 A infinite Real 0. 01496 A 0. 146 A 1. 2 A 6 A VR=RI 1. 496 V 1. 46 V 1. 2 V 0 V
 Which are the main group elements
Which are the main group elements What is a parallel circuit in physics
What is a parallel circuit in physics Urine sperm
Urine sperm Pyuria leukocytes urine
Pyuria leukocytes urine Macroscopic momentum balance
Macroscopic momentum balance Macroscopic energy balance
Macroscopic energy balance Csf cell count
Csf cell count Chemstix
Chemstix Macroscopic hematuria causes
Macroscopic hematuria causes Cheesy masses in sputum
Cheesy masses in sputum Continuity equation in electrodynamics
Continuity equation in electrodynamics Macroscopic electric field
Macroscopic electric field Macroscopic level meaning
Macroscopic level meaning Normal semen report
Normal semen report Cranial caudal
Cranial caudal Macroscopic description of an ideal gas
Macroscopic description of an ideal gas Phaeophyta unicellular multicellular
Phaeophyta unicellular multicellular Culuture definition
Culuture definition Sequential circuit analysis
Sequential circuit analysis Continues
Continues Analysis of sequential circuits
Analysis of sequential circuits Sinusoidal steady state analysis of coupled circuits
Sinusoidal steady state analysis of coupled circuits Instantaneous value of the emf phasor
Instantaneous value of the emf phasor Four resistor bias circuit
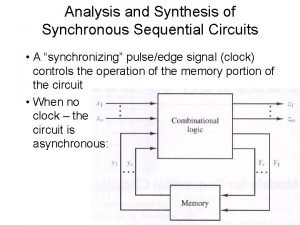
Four resistor bias circuit Analysis of synchronous sequential circuits
Analysis of synchronous sequential circuits Analysis of synchronous sequential circuits
Analysis of synchronous sequential circuits