List decoding ReedMuller codes up to minimal distance

List decoding Reed-Muller codes up to minimal distance: Structure and pseudorandomness in coding theory Abhishek Bhowmick (UT Austin) Shachar Lovett (UC San Diego)

What this talk is about? • Technically: new understanding of a basic and important family of codes • Conceptually: structure and pseudo-randomness play important roles in many computational domains. This talk shows this phenomena applied to coding theory

Overview • Coding theory 101 • Regularity in coding theory • Structural properties of polynomials • Pseudo-randomness for polynomials • Summary

Overview • Coding theory 101 • Regularity in coding theory • Structural properties of polynomials • Pseudo-randomness for polynomials • Summary

Decoding from errors • The basic problem of coding theory: recovering from errors • Goal: recover correct codeword from a noisy received word • This work: worst-case errors

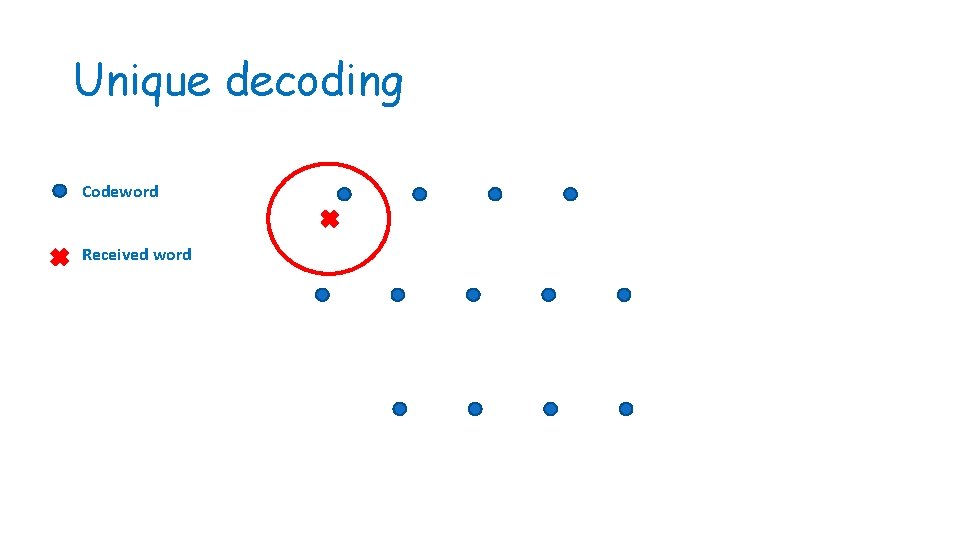
Unique decoding Codeword Received word

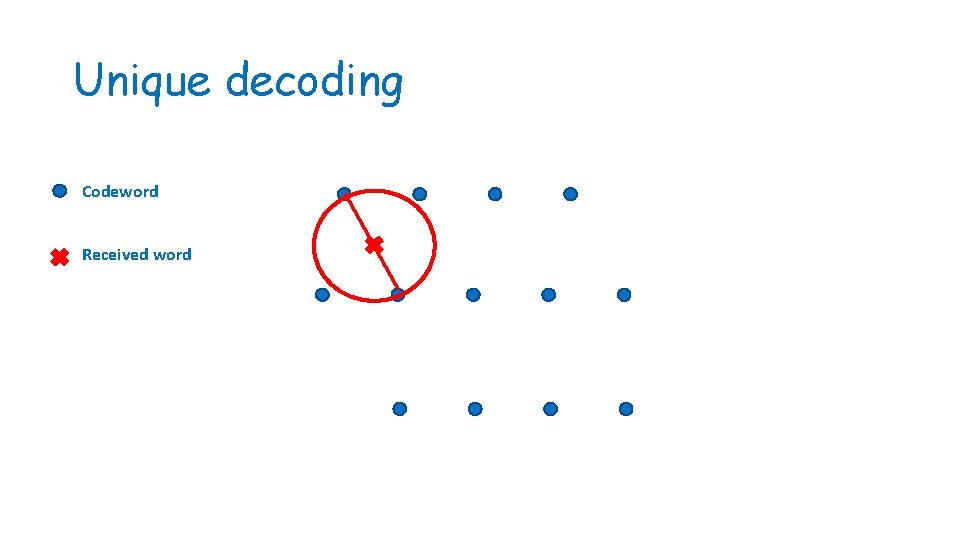
Unique decoding • Unique decoding: find the closest codeword • Basic limitation: minimal distance of the code • If a received word is “in between” two codewords, we cannot distinguish which is the correct codeword • Limits error to <½ the minimal distance

Unique decoding Codeword Received word

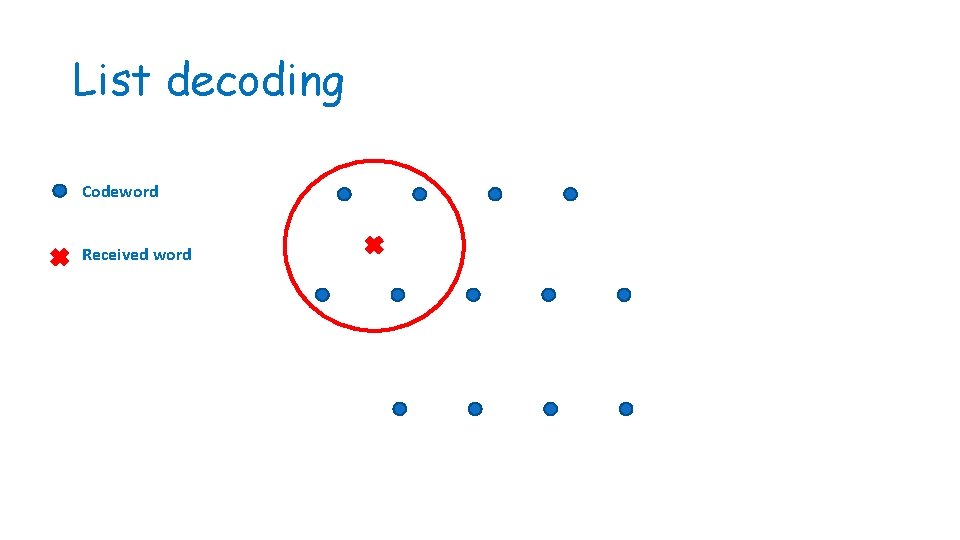
List decoding • List decoding: find few closest codewords [Elias ‘ 57] • Circumvents the ½ minimal distance problem • In general, can recover from errors up to Johnson bound ½ minimal distance < Johnson bound < minimal distance • For special codes (hmmm…) can do better

List decoding Codeword Received word

Polynomial codes • Most codes are based on polynomials • In this talk, focus on the most basic families • Reed-Solomon: univariate polynomials • Reed-Muller: multivariate polynomials • Despite (or because) being basic, they are widely applied; however, they are far from fully understood

Why polynomial codes? • Polynomial codes are “special” • Do they behave better than “worst-case” analysis? • Concretely: are they list decodable beyond the Johnson bound? • Previous works: yes • This work: YES

Reed-Muller codes •

Minimal distance of Reed-Muller codes •

Minimal distance of Reed-Muller codes •

Hadamard codes • Hadamard codes correspond to d=1 (linear functions) • Minimal distance=1/|F| • List decodable up to error 1/|F| [Goldreich-Levin’ 89, Goldreich-Rubinfeld-Sudan’ 00] • Proof: Fourier analysis

Large fields •

Small fields • Breakthrough in 2008: Over F 2, RM codes are list decodable up to minimal distance (combinatorially & algorithmically) [Gopalan-Klivans-Zuckerman’ 08] • Proof doesn’t extend to larger fields: uses special properties of Johnson bound over binary fields • GKZ conjecture: all RM codes are list decodable up to minimal distance (they are all “special”)

GKZ conjecture •

Main result (this work) •

Extension to large fields (in progress) •

Proof idea •

Overview • Coding theory 101 • Regularity in coding theory • Structural properties of polynomials • Pseudo-randomness for polynomials • Summary

The list decoding problem, revisited •

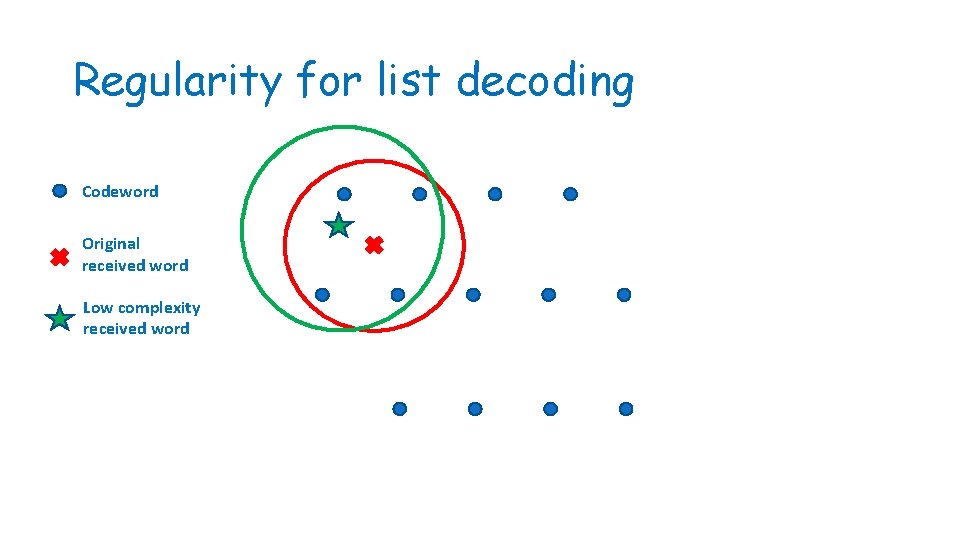
Regularity for list decoding • Lemma: for any code, any received word can be replaced by a “low complexity” received word, which is indistinguishable from the code perspective • Similar to the Frieze-Kannan weak regularity • Viewpoint: codewords are “tests”

Regularity for list decoding •

Regularity for list decoding Codeword Original received word Low complexity received word

Proof of regularity lemma •

Upshot •

Overview • Coding theory 101 • Regularity in coding theory • Structural properties of polynomials • Pseudo-randomness for polynomials • Summary

A very special case (which will turn out to be not so special) •

Rethinking minimal distance •

A structural lemma •

Proof of structural lemma •

Overview • Coding theory 101 • Regularity in coding theory • Structural properties of polynomials • Pseudo-randomness for polynomials • Summary

Pseudo-random polynomials •

Pseudo-random polynomials: examples •

A dichotomy theorem •

Decompositions of polynomials • The dichotomy theorem can be applied iteratively, to decompose any low-degree polynomial as a function of a few polynomials which are pseudo-random • To a large extent, pseudo-random polynomials behave as “independent variables” • Made precise in higher-order Fourier analysis

Going back to the very special case •

Overview • Coding theory 101 • Regularity in coding theory • Structural properties of polynomials • Pseudo-randomness for polynomials • Summary

Result • Reed-Muller codes are special: can be list decoded up to minimal distance (for constant degrees, fields) • Proof relies on three ingredients: 1. Regularity for codes 2. Structural property of RM codes (polynomials) 3. Pseudo-randomness for RM codes (polynomials)

Follow up work • We extend the current result to the case of large fields • This requires a few new ingredients: 1. Optimizing the arguments, to get a polynomial dependency on the field size 2. Extending higher-order Fourier to large fields, with bounds independent of field size

Take home message • Notions of structure and pseudo-randomness are very powerful; dichotomy theorems make them universal • This work: coding theory, applied to RM codes • Other applications: math - graph theory, number theory, ergodic theory, discrete geometry; CS - property testing, complexity, algorithms • Question: do our techniques generalize to other codes? domains? Other

Thank you!