Linear Hierarchical Models Corinne Giorgia MFD Giorgia Corinne

Linear Hierarchical Models Corinne Giorgia MFD Giorgia & Corinne Introduction/Overview & Examples (behavioral) functional Brain Imaging Examples, Fixed Effects Analysis vs. Random Effects Analysis

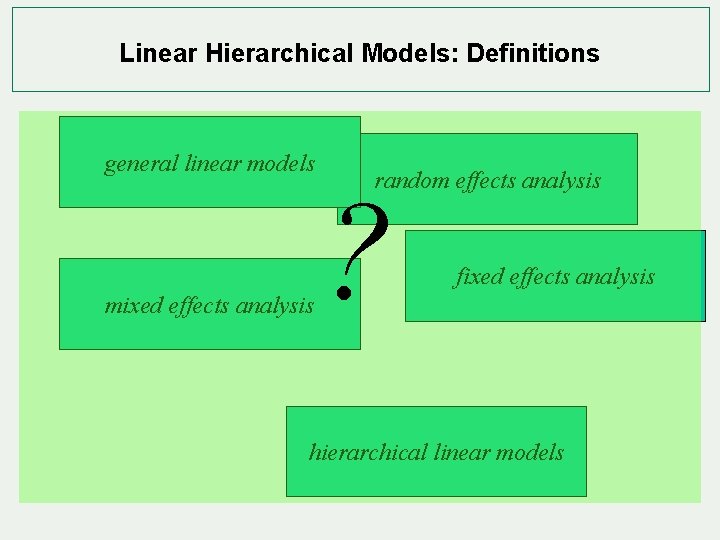
Linear Hierarchical Models: Definitions general linear models mixed effects analysis random effects analysis ? fixed effects analysis hierarchical linear models

Linear Hierarchical Models: Definitions Introduction » Penny, W. & Friston K. J. (2003) Human Brain Function » Hierarchical models are central to many current analyses of functional imaging data including random effects analysis, models using f. MRI as priors for EEG source localization and spatiotemporal Bayesian modelling of imaging data » These hierarchical models posit linear relations between variables with error terms that are Gaussian » The General Linear Model (GLM), which to date has been so central to the analysis of functional imaging data, is a special case of these hierarchical models consisting of just a single layer » Central to many analysis of functional imaging data (e. g. , random effects analysis) » Linear relations between variables » GLM = special HLM of just a single layer

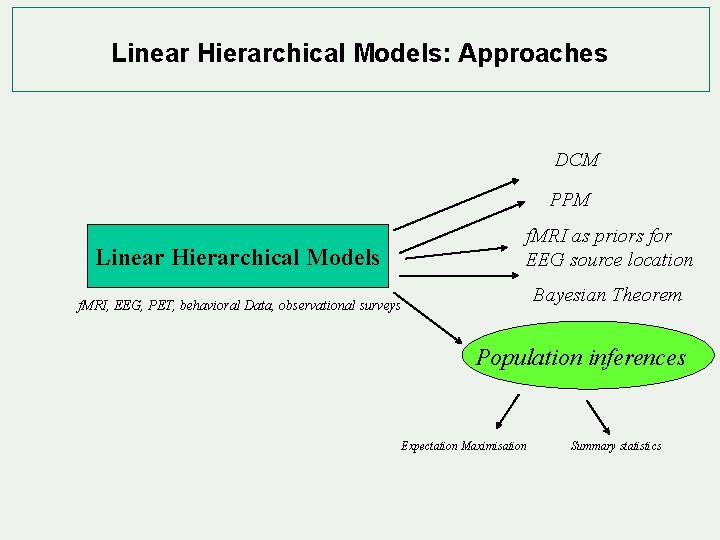
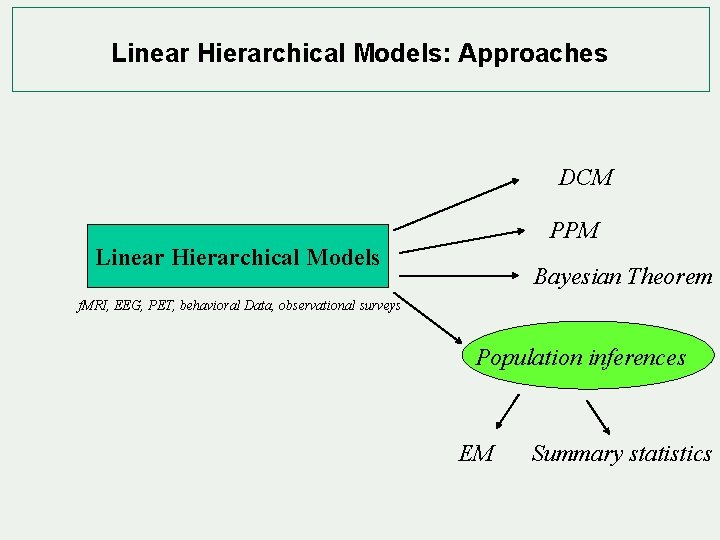
Linear Hierarchical Models: Approaches DCM PPM f. MRI as priors for EEG source location Linear Hierarchical Models Bayesian Theorem f. MRI, EEG, PET, behavioral Data, observational surveys Population inferences Expectation Maximisation Summary statistics

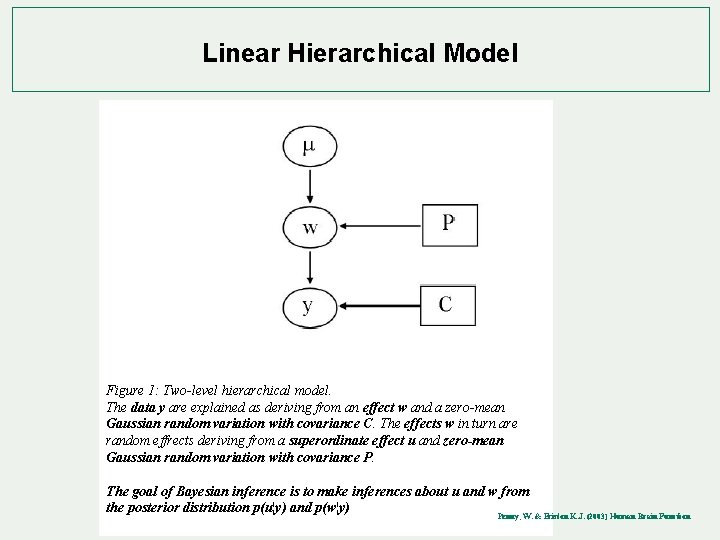
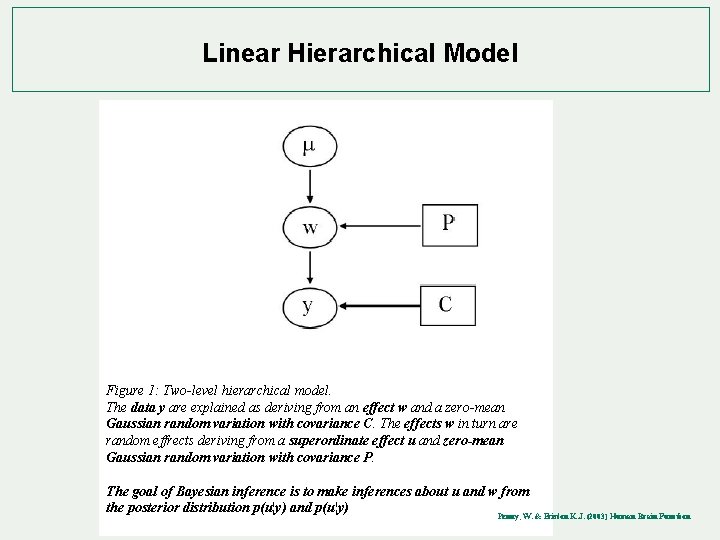
Linear Hierarchical Model Figure 1: Two-level hierarchical model. The data y are explained as deriving from an effect w and a zero-mean Gaussian random variation with covariance C. The effects w in turn are random effrects deriving from a superordinate effect u and zero-mean Gaussian random variation with covariance P. The goal of Bayesian inference is to make inferences about u and w from the posterior distribution p(u¦y) and p(w¦y) Penny, W. & Friston K. J. (2003) Human Brain Function

Linear Hierarchical Models: Definitions general linear models mixed effects analysis random effects analysis ? fixed effects analysis hierarchical linear models

Linear Hierarchical Models: Definitions general linear models mixed effects analysis random effects analysis ? fixed effects analysis hierarchical linear models

Linear Hierarchical Models: Definitions general linear models mixed effects analysis random effects analysis ? fixed effects analysis hierarchical linear models

Linear Hierarchical Models: Definitions general linear models mixed effects analysis random effects analysis ? fixed effects analysis hierarchical linear models

Linear Hierarchical Models: Definitions general linear models mixed effects analysis random effects analysis ? fixed effects analysis hierarchical linear models

Linear Hierarchical Models: General Definition: » Hierarchical Linear Models (HLM) incorporate data from multiple levels in an attempt to determine the impact of individual and grouping factors upon some individual level outcome Example » Student achievment as a function of student level characteristics (e. g. , IQ, study habits), classroom level factors (e. g. , instructions style, textbook), school level factors (e. g. , wealth), and so on. » HLMs or multilevel models can incorporate such factors in a manner better than ordinary least squares since HLMs take into account error structures at each level

Linear Hierarchical Models: Screening Example: » Dummies knowledge increase as a function of » Talk in Methods for Dummies » Research group (topic) » Previous knowledge level » GLM » » » 4 types of tests Dummies ID Research group ID Does the talk have a significant effect on knowledge increase? Suspecting research group having a significant effect talk_MFDtestdummies_rest. sav

Linear Hierarchical Models: Screening Example Results and Inferences of GLM: » There is a lot of variability in the „research group ID“, so it is an important effect to model; » Hence the model results cannot be generalized to other research groups as „research group ID“ is a fixed effect. » Aside from the first research group which generated considerably higher knowledge increase than the others, the research group effects seem to be randomly scattered (Gaussian Distribution) » Therefore, using another procedure, you might be able to specify „reserach group ID“ as a random effect » To use ordinary least squares with these data as „independent“ (exogenous) variables isn‘t right because of the correlations among Dummies in the same research field. » No inferences about other research groups dummies!

Linear Hierarchical Models: SPSS GLM: » Results: » first talk was more effective than the others » considerable variation in knowledge increase by factor research group » How to do generalization of these results to other Dummies? ! » GLM Repeated Measures procedure does not allow for random effects » GLM Univariate procedure does not allow for within-subjects effects Linear Mixed Model procedure: » specify research groups ID as a random effect » Gives greater control over the specification of the covariance matrix for the within-subjects factor » Models the mean of a response variable and its covariance structure » talk_MFDtestdummies_mntestres. sav

Linear Hierarchical Models: Screening Example Results and Inferences of linear mixed model procedure: » Fixed effects » Test significance values (that is, less than 0. 05) indicate that the effect research group contributes to the model talk_MFDFIXED EFFECTS. HTM » Estimates of the fixed model effects their significance talk_MFDESTIMATES OF FIXED EFFECTS. HTM » The individual effects of the first two talks are significantly different from the third » The estimates of the effects suggest that the first talk is the best, for it is associated with higher sales than either of the other promotions » Random effects » Estimates of Covariance Parametes » Random Effect Covariance Structure

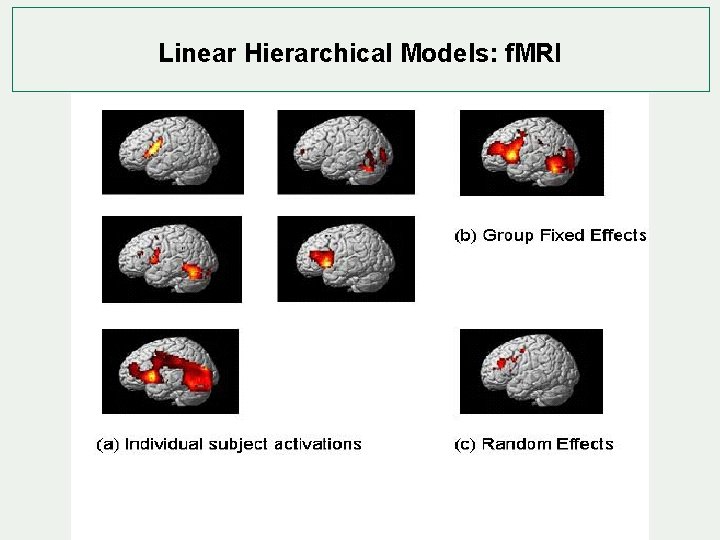
Linear Hierarchical Models: f. MRI Mixed model procedure = linear hierarchical model ? » Mixed model: » Fixed effects (1 st level, GLM) » Random effects (2 nd level, LHM) Why so important in f. MRI ? » Study design: » Single subjects study vs. studies invonlving many subjects » Individual differences vs. population effects » Trial to trial (within subjects) and subject to subject (between subjecs) » 2 levels of variance

Linear Hierarchical Models: f. MRI

Linear Hierarchical Model Figure 1: Two-level hierarchical model. The data y are explained as deriving from an effect w and a zero-mean Gaussian random variation with covariance C. The effects w in turn are random effrects deriving from a superordinate effect u and zero-mean Gaussian random variation with covariance P. The goal of Bayesian inference is to make inferences about u and w from the posterior distribution p(u¦y) and p(u¦y) Penny, W. & Friston K. J. (2003) Human Brain Function

Linear Hierarchical Model » Y = X(1) + e(1) (1 st level) – within subject : » (1) = X(2) + e(2) (2 nd level) – between subject » Y = scans from all subjects » X(n) = design matrix at nth level » (n) = parameters - basically the s of the GLM » e(n) = N(m, 2) error we assume there is a Gaussian distribution with a mean (m) and variation ( 2)

Linear Hierarchical Models: Considerations Assumptions » Dependent variable assumed to be linearly related to the fixed factors, random factors, and covariates. » The fixed effects model the mean of the dependent variable. » The random effects model the covariance structure of the dependent variable.

Linear Hierarchical Models: Considerations Assumptions » Related procedures » Examine the data before running an analysis » If you do not suspect there to be correlated or non-constant variability, you can alternatively use the GLM Univariate or GLM Repeated Measures procedure. » Correlated or non-constant variablility in f. MRI? ! » Limitations of SPM

Linear Hierarchical Models: Considerations » Solving the problems » By using the probability that a voxel had activated, or indeed its activation was greater than some threshold » likelihood of getting the data, given no activation » Classical approach » Probablility distribution of the activation given the data » posterior probability used in Bayesian inference » Posterior distribution needs » Likelihood, afforded by assumption about the distribution of errors » Prior probability of activation (as values or estimated from the data, provided we have observed multiple instances of the effect we are insterested in)

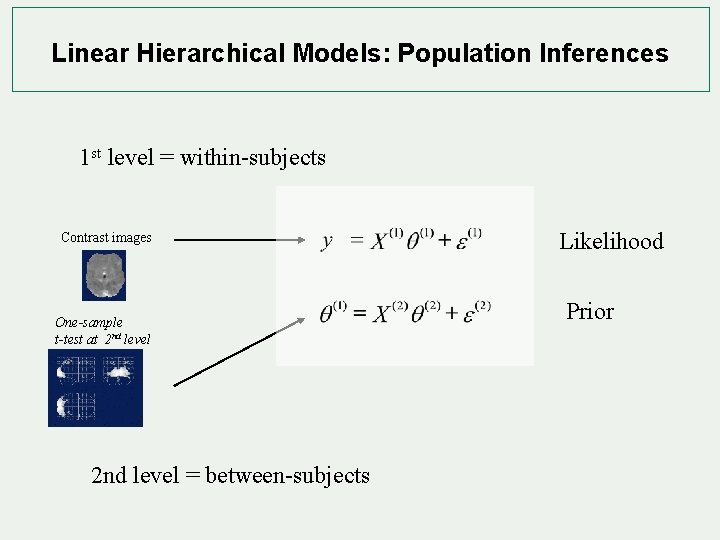
Linear Hierarchical Models: Population Inferences 1 st level = within-subjects Contrast images One-sample t-test at 2 nd level = between-subjects Likelihood Prior

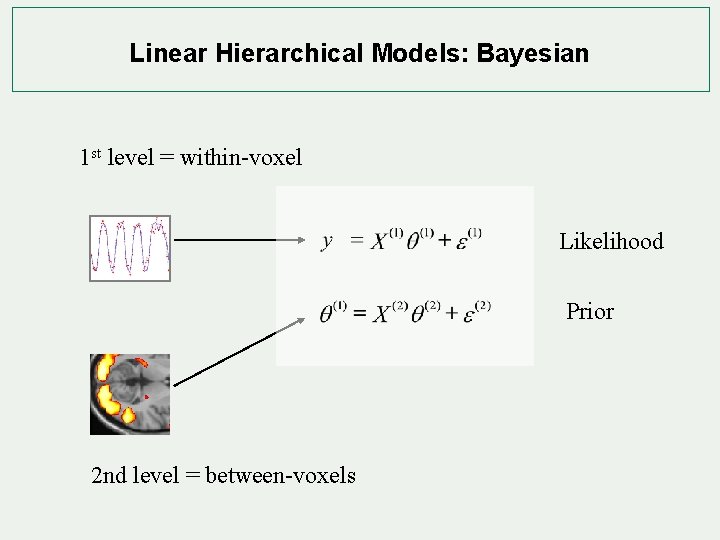
Linear Hierarchical Models: Bayesian 1 st level = within-voxel Likelihood Prior 2 nd level = between-voxels

Linear Hierarchical Models: Approaches DCM PPM Linear Hierarchical Models Bayesian Theorem f. MRI, EEG, PET, behavioral Data, observational surveys Population inferences EM Summary statistics

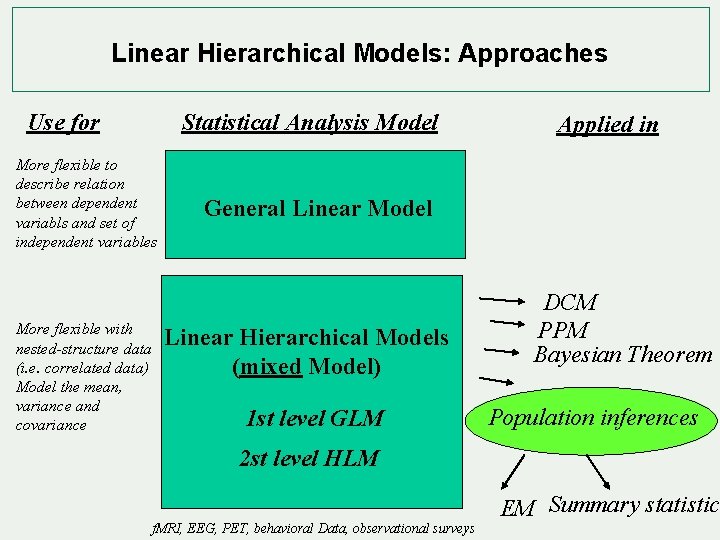
Linear Hierarchical Models: Approaches Use for Statistical Analysis Model More flexible to describe relation between dependent variabls and set of independent variables More flexible with nested-structure data (i. e. correlated data) Model the mean, variance and covariance Applied in General Linear Model Linear Hierarchical Models (mixed Model) 1 st level GLM DCM PPM Bayesian Theorem Population inferences 2 st level HLM f. MRI, EEG, PET, behavioral Data, observational surveys EM Summary statistics

Linear Hierarchical Models: Definitions general linear models mixed effects analysis random effects analysis ! fixed effects analysis hierarchical linear models

Linear Hierarchical Models: Definitions general linear models mixed effects analysis random effects analysis ! fixed effects analysis -> SPM: Giorgia -> more detail SPM course …. hierarchical linear models