Hierarchical Linear Models Optimizing Iterating ctd Peter Fox

Hierarchical Linear Models, Optimizing, Iterating ctd. Peter Fox and Greg Hughes Data Analytics – ITWS-4600/ITWS-6600 Group 4 Module 14, April 17, 2017 1

Iterating: structure to regression • Hierarchical … simpler form of mixed model? 2

Remember: Random effects. . In the initial exploiration class as nested within school, “class is 'under' school”, specified inside parentheses and can be repeated measures, interaction terms, or nested lmm. 1 <- lmer(extro ~ open + social + class + (1|school/class), data = lmm. data) summary(lmm. 1) 3

Summary(lmm. 1) Linear mixed model fit by REML ['lmer. Mod'] Formula: extro ~ open + social + class + (1 | school/class) Data: lmm. data REML criterion at convergence: 3521. 5 Scaled residuals: Min 1 Q Median 3 Q Max -10. 0144 -0. 3373 0. 0164 0. 3378 10. 5788 Random effects: Groups Name Variance Std. Dev. class: school (Intercept) 2. 8822 1. 6977 school (Intercept) 95. 1725 9. 7556 Residual 0. 9691 0. 9844 Number of obs: 1200, groups: class: school, 24; school, 6 4

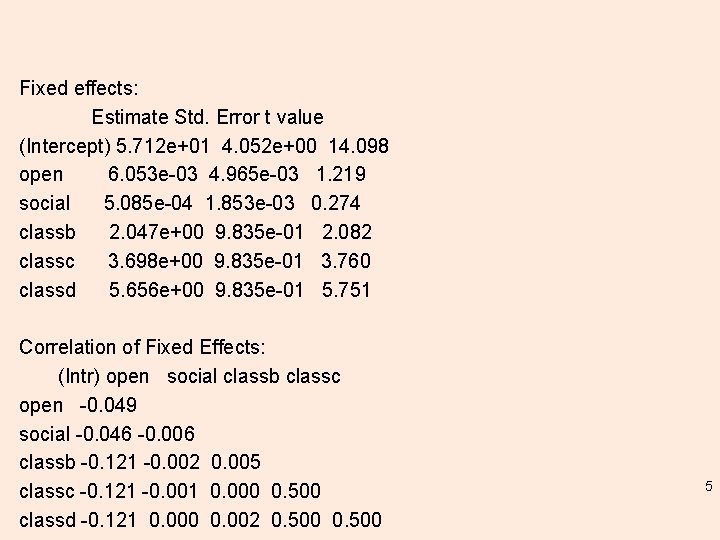
Fixed effects: Estimate Std. Error t value (Intercept) 5. 712 e+01 4. 052 e+00 14. 098 open 6. 053 e-03 4. 965 e-03 1. 219 social 5. 085 e-04 1. 853 e-03 0. 274 classb 2. 047 e+00 9. 835 e-01 2. 082 classc 3. 698 e+00 9. 835 e-01 3. 760 classd 5. 656 e+00 9. 835 e-01 5. 751 Correlation of Fixed Effects: (Intr) open social classb classc open -0. 049 social -0. 046 -0. 006 classb -0. 121 -0. 002 0. 005 classc -0. 121 -0. 001 0. 000 0. 500 classd -0. 121 0. 000 0. 002 0. 500 5

Now: Intra Class Correlation # First, run the 'null' model (which includes just the intercepts and the random effect for the highest level of the nesting variables; in this example 'school’. lmm. null <- lmer(extro ~ 1 + (1|school), data = lmm. data) summary(lmm. null) 6

summary Linear mixed model fit by REML ['lmer. Mod'] Formula: extro ~ 1 + (1 | school) Data: lmm. data REML criterion at convergence: 5806. 1 Scaled residuals: Min 1 Q Median 3 Q Max -5. 9773 -0. 5315 0. 0059 0. 5298 6. 2109 Random effects: Groups Name Variance Std. Dev. school (Intercept) 95. 87 9. 791 Residual 7. 14 2. 672 Number of obs: 1200, groups: school, 6 Fixed effects: Estimate Std. Error t value (Intercept) 60. 267 3. 998 15. 07 7

Intra Class Correlation (ICC) # Notice the variance component estimates for the random effect. If we add these together, then divide that total by the 'school' variance estimate; we get the ICC 95. 8720 + 7. 1399 95. 8720 / 103. 0119 # This indicates that 93. 06886% of the variance in 'extro' can be "explained" by school group membership (verified below using Bliese's multilevel package). 8

# ICC 1 and ICC 2 as described by Bliese. library(multilevel) aov. 1 <- aov(extro ~ school, lmm. data) summary(aov. 1) Df Sum Sq Mean Sq F value Pr(>F) school 5 95908 19182 2687 <2 e-16 *** Residuals 1194 8525 7 --Signif. codes: 0 ‘***’ 0. 001 ‘**’ 0. 01 ‘*’ 0. 05 ‘. ’ 0. 1 ‘ ’ 1 9

ICC 1/ ICC 2 (Bliese) # Below (ICC 1) indicates that 93. 07% of the variance in 'extro' can be "explained" by school # group membership. ICC 1(aov. 1) [1] 0. 930689 # The ICC 2 value (below) of. 9996 indicates that school groups can be very reliably differentiated in terms of 'extro' scores. > ICC 2(aov. 1) [1] 0. 9996278 10

Simulating the Posterior Distribution of Predicted Values. # 'arm' package and use the 'sim' function. Note: n = 100 is the default for 'sim’. library(arm) sim. 100 <- sim(lmm. 2, n = 100) # Show the structure of objects in the 'sim' object. str(sim. 100) <not displayed> 11

Simulating the Posterior Distribution of Predicted Values. # Fixed effect parameter estimates resulting from the 'sim' function applied to the fitted model (lmm. 3). fe. sim <- fixef(sim. 100) fe. sim (Intercept) open agree social classb classc classd [1, ] 55. 24643 0. 0113879890 -7. 370662 e-03 4. 115703 e-03 1. 99092257 2. 9418821 3. 162604 [2, ] 56. 69630 0. 0051451242 -1. 373704 e-02 -1. 799054 e-03 1. 73041539 3. 8671053 6. 160748 [3, ] 63. 18570 0. 0003935109 2. 607783 e-03 1. 435752 e-03 1. 80586410 3. 2203590 5. 802364 [4, ] 56. 00007 0. 0042571840 -6. 076147 e-03 -5. 324692 e-03 2. 71728164 5. 6066533 6. 852651 [5, ] 59. 94718 0. 0026340937 -2. 584516 e-03 3. 295548 e-07 1. 45650055 3. 3174045 5. 871667 [6, ] 65. 26589 0. 0100470520 -1. 324052 e-02 -3. 480780 e-04 1. 79030239 3. 3253023 4. 050358 [7, ] 56. 80116 0. 0082074105 -8. 175804 e-03 1. 182413 e-03 2. 35693946 3. 0119753 5. 937348 [8, ] 61. 32350 0. 0047934705 -1. 484498 e-02 -2. 710392 e-03 2. 11558934 4. 2048688 6. 552194 [9, ] 53. 87001 0. 0054213155 -7. 160089 e-03 8. 668833 e-04 1. 86080451 2. 8613245 4. 761669 [10, ] 57. 47641 0. 0055136083 -6. 293459 e-03 -5. 253847 e-05 3. 17600677 6. 4525022 6. 438270 12

Simulating the Posterior Distribution of Predicted Values. # Random effect parameter estimates resulting from the 'sim' function applied to the fitted model (lmm. 3). re. sim <- ranef(sim. 100) re. sim[[1]] # For "class: school" random effect. re. sim[[2]] # For ”school" random effect. 13

re. sim[[1]] # For ”class: school" random effect. , , (Intercept) a: III a: IV a: VI b: II [1, ] -1. 8138575 1. 009722294 0. 502308352 0. 574242632 1. 62249792 0. 34486828 0. 41734749 -0. 516721008 [2, ] -4. 5023927 0. 325461572 1. 105711427 0. 555938715 1. 49927806 -1. 05082790 0. 72720272 1. 065476210 [3, ] -2. 9011592 1. 699112086 1. 924096930 1. 588047483 0. 08551292 -1. 71333314 0. 47475579 0. 095562455 [4, ] -4. 7454517 -1. 024665550 0. 449287566 1. 066899463 1. 56470696 -1. 34450134 -0. 47980863 0. 964331898 [5, ] -4. 6413961 0. 092845610 0. 878011579 0. 328065852 0. 94227622 -2. 48685750 0. 13250051 0. 336973705 Much more! 14

re. sim[[2]] # For "school" random effect. , , (Intercept) I II IV V VI [1, ] -10. 889610 11. 9319979 6. 4468727 7. 52046579 9. 407021912 14. 8484638 [2, ] -11. 811196 -10. 1548630 -2. 3812528 4. 24907315 6. 038850618 15. 1022442 [3, ] -17. 642004 -6. 5881409 2. 6734584 5. 09687885 7. 313420709 7. 6798984 [4, ] -12. 201235 -6. 5415744 -6. 2550322 4. 62112286 13. 050521302 14. 7147714 [5, ] -16. 604904 -10. 9215257 -3. 2698478 2. 47299902 2. 276550540 11. 8441601 15

Get predicted values # To get predicted values from the posterior distribution, use the 'fitted' function. yhat. lmm. 2 <- fitted(sim. 100, lmm. 2) head(yhat. lmm. 2) < see output > tail(yhat. lmm. 2) < see output > 16

# The above object (yhat. lmm. 2) is a matrix of 100 (simulations) by 1200 participants. # In this matrix, each row represents a participant and each column represents a simulated predicted value for the outcome variable of our lmm. 2 model. # Therefore, the yhat. lmm. 2 object can be used to create credible intervals for each participant (i. e. individual level). > quantile(yhat. lmm. 2, probs = c(. 025, . 985)) # For first participant (i. e. row 1). 2. 5% 98. 5% 39. 93096 81. 29584 17

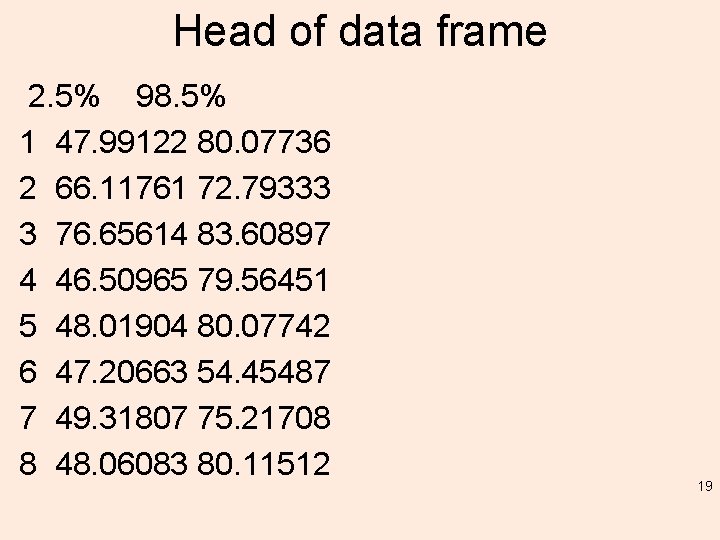
# We can also create a data frame with the quantiles for every participant. quant. mat <- data. frame(matrix(rep(NA, 1200*2), ncol = 2)) names(quant. mat) <- c("2. 5%", "98. 5%") quant. mat[, 1] <- apply(yhat. lmm. 2, 1, quantile, probs =. 025) quant. mat[, 2] <- apply(yhat. lmm. 2, 1, quantile, probs =. 985) head(quant. mat, 25) 18

Head of data frame 2. 5% 98. 5% 1 47. 99122 80. 07736 2 66. 11761 72. 79333 3 76. 65614 83. 60897 4 46. 50965 79. 56451 5 48. 01904 80. 07742 6 47. 20663 54. 45487 7 49. 31807 75. 21708 8 48. 06083 80. 11512 19

In R - lcmm • Estimation of latent class mixed-effect models for different types of outcomes (continuous Gaussian, continuous non-Gaussian or ordinal) • This function fits mixed models and latent class mixed models for different types of outcomes. – continuous longitudinal outcomes (Gaussian or non-Gaussian) as well as bounded quantitative, discrete and ordinal longitudinal outcomes. 20

What does it do? • The different types of outcomes are taken into account using parameterized nonlinear link functions between the observed outcome and the underlying latent process of interest • At the latent process level, the model estimates a standard linear mixed model or a latent class mixed model when heterogeneity in the population is investigated (in the same way as in function hlme -> next) but it should be noted that the program also works when 21 no random-effect is included!

What does it do? • Parameters of the nonlinear link function and of the latent process mixed model are estimated simultaneously using a maximum likelihood method. lcmm(fixed, mixture, random, subject, classmb, ng = 1, idiag = FALSE, nwg = FALSE, link = "linear", intnodes = NULL, eps. Y = 0. 5, data, B, conv. B = 1 e-04, conv. L = 1 e-04, conv. G = 1 e-04, maxiter=100, nsim=100, prior, range=NULL, na. action=1) ### that’s a lot of parameters 22

Turning to lcmm # Beta link function m 11<-lcmm(Ydep 2~Time+I(Time^2), random=~Time, subject='ID', ng=1, data=data_Jointlcmm, link="beta") summary(m 11) plot. linkfunction(m 11, bty="l") # I-splines with 3 equidistant nodes m 12<-lcmm(Ydep 2~Time+I(Time^2), random=~Time, subject='ID', ng=1, data=data_Jointlcmm, link="3 -equi-splines") summary(m 12) # I-splines with 5 nodes at quantiles m 13<-lcmm(Ydep 2~Time+I(Time^2), random=~Time, subject='ID', ng=1, data=data_Jointlcmm, link="5 -quant-splines") summary(m 13) # I-splines with 5 nodes, and interior nodes entered manually m 14<-lcmm(Ydep 2~Time+I(Time^2), random=~Time, subject='ID', ng=1, data=data_Jointlcmm, link="5 -manual-splines", intnodes=c(10, 25)) summary(m 14) plot. linkfunction(m 14, bty="l") 23

Turning to lcmm # Thresholds # Especially for the threshold link function, we recommend to estimate models # with increasing complexity and use estimates of previous ones to specify # plausible initial values (we remind that estimation of models with threshold # link function involves a computationally demanding numerical integration # -here of size 3) m 15<-lcmm(Ydep 2~Time+I(Time^2), random=~Time, subject='ID', ng=1 , data=data_Jointlcmm, link="thresholds", maxiter=100, B=c(-0. 8379, -0. 1103, 0. 3832, 0. 3788 , 0. 4524, -7. 3180, 0. 5917, 0. 7364, 0. 6530, 0. 4038, 0. 4290, 0. 6099, 0. 6014 , 0. 5354 , 0. 5029 , 0. 5463, 0. 5310 , 0. 5352, 0. 6498, 0. 6653, 0. 5851, 0. 6525, 0. 6701 , 0. 6670 , 0. 6767 , 0. 7394 , 0. 7426, 0. 7153, 0. 7702, 0. 6421)) summary(m 15) plot. linkfunction(m 15, bty="l") 24

Turning to lcmm #### Plot of estimated different link functions: #### (applicable for models that only differ in the "link function" used. #### Otherwise, the latent process scale is different and a rescaling is necessary) transfo <- data. frame(marker=m 10$estimlink[, 1], linear=m 10$estimlink[, 2], beta=m 11$estimlink[, 2], spl_3 e=m 12$estimlink[, 2], spl_5 q=m 13$estimlink[, 2], spl_5 m=m 14$estimlink[, 2]) dev. new() plot(transfo[, 1]~transfo[, 2], xlim=c(-10, 5), col=1, type='l', xlab="latent process", ylab="marker", bty="l") par(new=TRUE) plot(transfo[, 1]~transfo[, 3], xlim=c(-10, 5), col=2, type='l', xlab="", ylab="", bty="l") par(new=TRUE) plot(transfo[, 1]~transfo[, 4], xlim=c(-10, 5), col=3, type='l', xlab="", ylab="", bty="l") par(new=TRUE) plot(transfo[, 1]~transfo[, 5], xlim=c(-10, 5), col=4, type='l', xlab="", ylab="", bty="l") par(new=TRUE) plot(m 15$estimlink[, 1]~m 15$estimlink[, 2], xlim=c(-10, 5), col=5, type='l' , xlab="", ylab="", bty="l") legend(x="bottomright", legend=c(colnames(transfo[, 2: 5]), "thresholds"), col=1: 5, lty=1, inset=. 02, bty="n”) 25

Turning to lcmm #### Estimation of 2 -latent class mixed models with different assumed link #### functions with individual and class specific linear trend #### for illustration, only default initial values where used but other #### sets of initial values should also be tried to ensure convergence #### towards the golbal maximum # Linear link function m 20<-lcmm(Ydep 2~Time, random=~Time, subject='ID', mixture=~Time, ng=2, idiag=TRUE, data=data_Jointlcmm, link="linear") summary(m 20) postprob(m 20) # Beta link function m 21<-lcmm(Ydep 2~Time, random=~Time, subject='ID', mixture=~Time, ng=2, idiag=TRUE, data=data_Jointlcmm, link="beta") summary(m 21) postprob(m 21) # I-splines link function (and 5 nodes at quantiles) m 22<-lcmm(Ydep 2~Time, random=~Time, subject='ID', mixture=~Time, ng=2, idiag=TRUE, data=data_Jointlcmm, link="5 -quant-splines") summary(m 22) postprob(m 22) 26 data <- data_Jointlcmm[data_Jointlcmm$ID==193, ] plot. predict(m 22, var. time="Time", newdata=data, bty="l")

Turning to multlcmm library(lcmm) data(data_Jointlcmm) # linear link function # Latent process mixed model for two curvilinear outcomes. Link functions are aproximated by I-splines, the first one has 3 nodes (i. e. 1 internal node 8), the second one has 4 nodes (i. e. 2 internal nodes 12, 25) m 1 <multlcmm(Ydep 1+Ydep 2~1+Time*X 2+contrast(X 2), random=~1+Time, subject="ID", random. Y=TRUE, link=c("4 -manual-splines", "3 -manual -splines"), intnodes=c(8, 12, 25), data=data_Jointlcmm) Be patient, multlcmm is running. . . The program took 56. 14 seconds 27

Quicker lcmm # to reduce the computation time, the same model is estimated using # a vector of initial values m 1 <multlcmm(Ydep 1+Ydep 2~1+Time*X 2+contrast(X 2), random=~1+Time, subject="ID", random. Y=TRUE, link=c("4 -manual-splines", "3 -manual -splines"), intnodes=c(8, 12, 25), data=data_Jointlcmm, B=c(-1. 071, -0. 192, 0. 106, -0. 005, -0. 193, 1. 012, 0. 870, 0. 881, 0. 000, -7. 520, 1. 401, 1. 607 , 1. 908, 1. 431, 1. 082, -7. 528, 1. 135 , 1. 454 , 2. 328, 1. 052)) Be patient, multlcmm is running. . . The program took 7. 78 seconds 28

Summary(m 1) General latent class mixed model fitted by maximum likelihood method multlcmm(fixed = Ydep 1 + Ydep 2 ~ 1 + Time * X 2 + contrast(X 2), random = ~1 + Time, subject = "ID", random. Y = TRUE, link = c("4 -manual -splines", "3 -manual-splines"), intnodes = c(8, 12, 25), data = data_Jointlcmm) Statistical Model: Dataset: data_Jointlcmm Number of subjects: 300 Number of observations: 3356 Number of latent classes: 1 Number of parameters: 21 Link functions: Quadratic I-splines with nodes 0 8 12 17. 581 for Ydep 1 Quadratic I-splines with nodes 0 25 30 for Ydep 2 29

Summary(m 1) Iteration process: Convergence criteria satisfied Number of iterations: 4 Convergence criteria: parameters= 5. 2 e-11 : likelihood= 2. 1 e-08 : second derivatives= 1. 2 e-09 Goodness-of-fit statistics: maximum log-likelihood: -6977. 48 AIC: 13996. 95 BIC: 14074. 73 30

Summary(m 1) Maximum Likelihood Estimates: Fixed effects in the longitudinal model: coef Se Wald p-value intercept (not estimated) 0. 00000 Time -1. 07056 0. 12293 -8. 70900 0. 00000 X 2 -0. 19225 0. 16697 -1. 15100 0. 24957 Time: X 2 0. 10627 0. 18634 0. 57000 0. 56847 Contrasts on X 2 (p=0. 88696) Ydep 1 -0. 00483 0. 03399 -0. 14215 0. 88696 Ydep 2* 0. 00483 0. 03399 0. 14215 0. 88696 *coefficient not estimated but obtained from the others as minus the sum of them Variance-covariance matrix of the random-effects: (the variance of the first random effect is not estimated) intercept Time intercept 1. 00000 Time -0. 19338 1. 01251 31

Summary(m 1) – last bit! Ydep 1 Ydep 2 Residual standard error: 0. 86955 0. 88053 Standard error of the random effect: 0. 00000 Parameters of the link functions: coef Se Wald p-value Ydep 1 -I-splines 1 -7. 51985 0. 64412 -11. 675 0 e+00 Ydep 1 -I-splines 2 1. 40067 0. 18058 7. 756 0 e+00 Ydep 1 -I-splines 3 1. 60739 0. 10324 15. 569 0 e+00 Ydep 1 -I-splines 4 1. 90822 0. 07873 24. 238 0 e+00 Ydep 1 -I-splines 5 1. 43117 0. 09075 15. 770 0 e+00 Ydep 1 -I-splines 6 1. 08205 0. 21198 5. 105 0 e+00 Ydep 2 -I-splines 1 -7. 52861 0. 67080 -11. 223 0 e+00 Ydep 2 -I-splines 2 1. 13505 0. 25553 4. 442 1 e-05 Ydep 2 -I-splines 3 1. 45345 0. 14629 9. 935 0 e+00 Ydep 2 -I-splines 4 2. 32793 0. 08636 26. 956 0 e+00 Ydep 2 -I-splines 5 1. 05187 0. 05908 17. 803 0 e+00 32

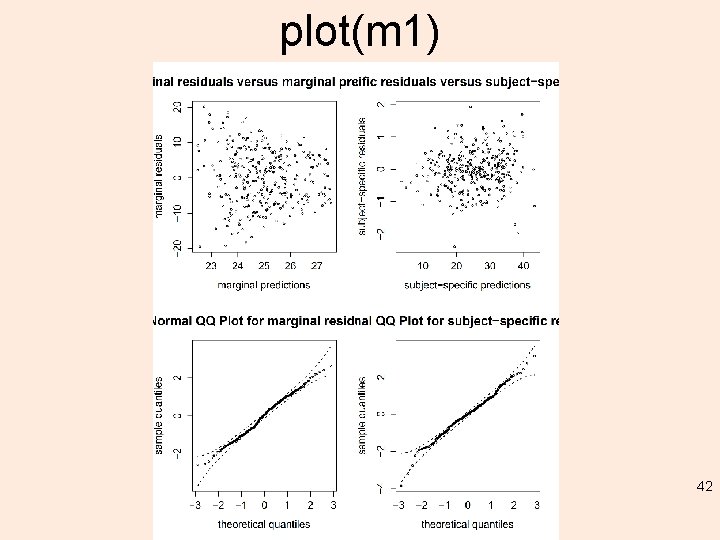
plot(m 1, which="linkfunction") # variation percentages explained by linear mixed regression > Var. Expl(m 1, data. frame(Time=0)) class 1 %Var-Ydep 1 56. 94364 %Var-Ydep 2 56. 32753 33

summary(m 2) <…> # posterior classification postprob(m 2) Posterior classification: class 1 class 2 N 143. 00 157. 00 % 47. 67 52. 33 Posterior classification table: --> mean of posterior probabilities in each class prob 1 prob 2 class 1 1. 0000 0. 0000 class 2 0. 0589 0. 9411 Posterior probalities above a threshold (%): class 1 class 2 prob>0. 7 100 98. 09 Prob>0. 8 100 96. 18 prob>0. 9 100 85. 99 34

# longitudinal predictions in the outcomes scales for a given profile of covariates newdata <data. frame(Time=seq(0, 5, length=100), X 1=rep(0, 100), X 2=rep(0, 100), X 3=rep(0, 100)) pred. GH <predict. Y(m 2, newdata, var. time="Time", meth. Integ=0, ns im=20) head(pred. GH) Etc. 35

In lcmm - hlme • Fits a latent class linear mixed model (LCLMM) also known as growth mixture model or heterogeneous linear mixed model. • LCLMM consists in assuming that the population is divided in a finite number of latent classes; each latent class is characterized by a specific mean trajectory which is described by a class-specific linear mixed model. • Both the latent class membership and the trajectory can be explained according to covariates. • This model is limited to a Gaussian outcome. 36

In R hlme(fixed, mixture, random, subject, classmb, ng = 1, idiag = FALSE, nwg = FALSE, cor=NULL, data, B, conv. B=0. 0001, conv. L=0. 0001, conv. G=0. 0001, prior, maxiter=500, subset=NULL, na. action=1) 37

Example data(data_hlme) m 1<-hlme(Y~Time*X 1, random=~Time, subject='ID', ng=1, idiag=TRUE, data=data_hlme) summary(m 1) 38

Summary hlme Heterogenous linear mixed model fitted by maximum likelihood method hlme(fixed = Y ~ Time * X 1, random = ~Time, subject = "ID", ng = 1, idiag = TRUE, data = data_hlme) Statistical Model: Dataset: data_hlme Number of subjects: 100 Number of observations: 326 Number of latent classes: 1 Number of parameters: 7 39

Summary hlme Iteration process: Convergence criteria satisfied Number of iterations: 9 Convergence criteria: parameters= 1. 2 e-07 : likelihood= 1. 6 e-05 : second derivatives= 6. 2 e-13 Goodness-of-fit statistics: maximum log-likelihood: -804. 98 AIC: 1623. 95 BIC: 1642. 19 Maximum Likelihood Estimates: Fixed effects in the longitudinal model: coef Se Wald p-value intercept 25. 86515 0. 79448 32. 556 0. 00000 Time -0. 33282 0. 17547 -1. 897 0. 05787 X 1 1. 69698 1. 03466 1. 640 0. 10098 Time: X 1 -0. 39364 0. 22848 -1. 723 0. 08491 40

Summary hlme Variance-covariance matrix of the random-effects: intercept Time intercept 24. 63032 Time 0. 00000 1. 168762 coef se Residual standard error: 0. 9501876 0. 05765784 41

plot(m 1) 42

Example m 2<-hlme(Y~Time*X 1, mixture=~Time, random=~Time, classmb=~X 2+X 3, subject='ID', ng=2, data=data_hlme, B=c(0. 11, -0. 74, -0. 07, 20. 71, 29. 39, -1, 0. 13, 2. 45, -0. 29, 4. 5, 0. 36, 0. 79, 0. 97)) Iteration process: m 2 Convergence criteria satisfied Number of iterations: 2 Convergence criteria: parameters= 1. 3 e-07 : likelihood= 4. 4 e-07 hlme(fixed = Y ~ Time * X 1, mixture = ~Time, random = ~Time, : second derivatives= 2. 5 e-12 Heterogenous linear mixed model fitted by maximum likelihood method subject = "ID", classmb = ~X 2 + X 3, ng = 2, data = data_hlme) Statistical Model: Dataset: data_hlme Number of subjects: 100 Number of observations: 326 Number of latent classes: 2 Number of parameters: 13 Goodness-of-fit statistics: maximum log-likelihood: -773. 82 AIC: 1573. 64 BIC: 1607. 51 43

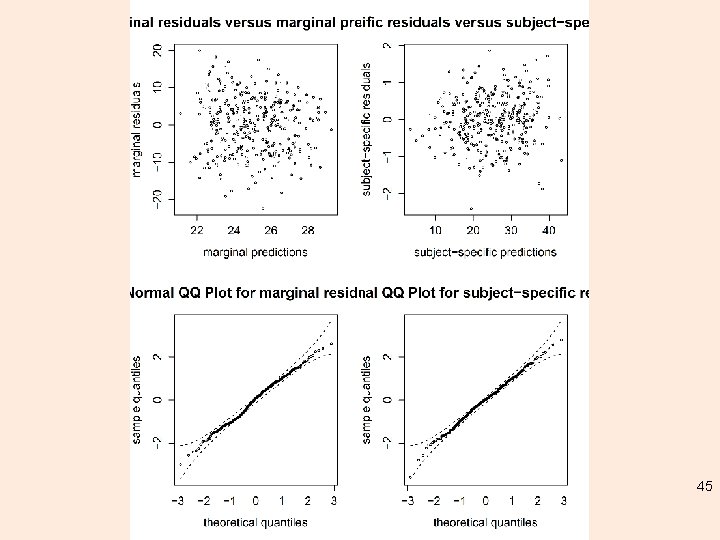
Example summary(m 2) postprob(m 2) Posterior classification: class 1 class 2 N 46 54 % 46 54 Posterior classification table: --> mean of posterior probabilities in each class prob 1 prob 2 class 1 0. 9588 0. 0412 class 2 0. 0325 0. 9675 Posterior probalities above a threshold (%): class 1 class 2 prob>0. 7 93. 48 100. 00 prob>0. 8 93. 48 92. 59 prob>0. 9 86. 96 83. 33 44

45

Example ### same model as m 2 but initial values specified m 3<-hlme(Y~Time*X 1, mixture=~Time, random=~Time, classmb=~X 2+X 3, subject='ID', ng=2, data=data_hlme, B=c(0, 0, 0, 30, 25, 0, -1, 0, 0, 5, 0, 1, 1)) m 3 46

Predicting… summary(m 3) Etc. ## plot of predicted trajectories using some newdata<-data. frame( Time= seq(0, 5, length=100), X 1= rep(0, 100), X 2=rep(0, 100), X 3=rep(0, 100)) plot. predict(m 3, newdata, "Time", "right", bty="l") 47

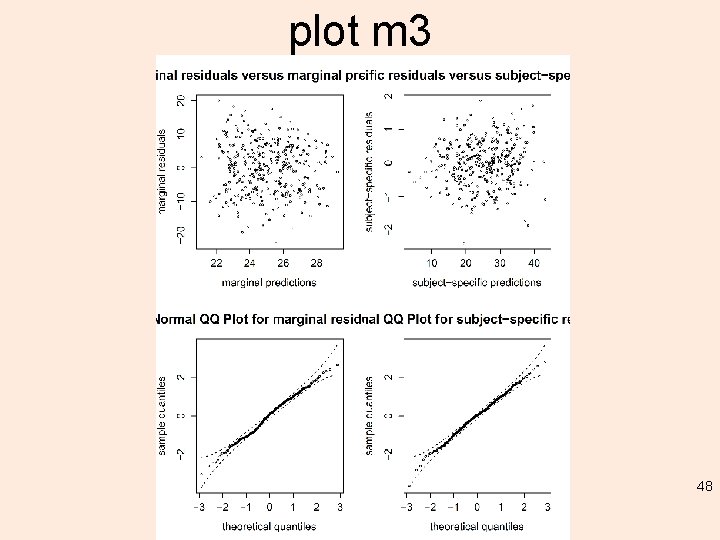
plot m 3 48

Beyond PCA! • Kernel PCA • ICA – PCA is not particularly helpful for finding independent clusters – ICA idea: – Assume non-Gaussian data – Find multiple sets of components – Minimize correlation between components – Blind source separation example: – Given: Audio recording with w/2 overlapping voices – Goal: Separate voices into separate tracks 49

Beyond PCA! Probabilistic PCA Bayesian source separation Continuous Latent Variables 50

Reading, etc. • http: //data-informed. com/focus-predictiveanalytics/ • Final weeks – final project presentations – Monday, Thursday, Monday – we cannot run over the class time to complete these – plan accordingly, arrive on time (instructions and initial schedule sent in LMS) – and attendance is very important • 4 MINUTES – you do not need more 51