Lgica Proposicional Deduo Natural Conseqncia lgica n Definio

Lógica Proposicional Dedução Natural

Conseqüência lógica n Definição informal: n n Uma fórmula é uma conseqüência lógica de um conjunto de fórmulas se sempre que estas forem verdadeiras aquela também seja verdadeira. Definição formal: n Dada uma fórmula H e um conjunto de hipóteses b, H é conseqüência lógica de b num sistema de dedução, se existir uma prova de H a partir de b

Notação de Conseqüência Lógica e Teorema n n Dada uma fórmula H, se H é conseqüência lógica de um conjunto de hipóteses b={H 1, H 2, . . . Hn}, diz-se que: n b├ H ou n {H 1, H 2, . . . Hn}├ H Uma fórmula H é um teorema se existe uma prova de H que não usa hipóteses n ├ H

Cálculo Proposicional n n Cálculo = Lógica + Sistema de Prova (ou dedução) Um sistema de prova serve para analisar e raciocinar sobre argumentos de uma lógica, de maneira a prová-los válidos ou inválidos.

Sistema de dedução natural n n n Alfabeto da Lógica Proposicional Conjunto de fórmulas da Lógica Proposicional Conjunto de regras de dedução (ou regras de inferência)

Regras de inferência de dedução natural n Servem para inserção e retirada de conectivos lógicos, criando derivações n n n Regras de Introdução Regras de Eliminação Chama-se dedução natural por estar próxima da maneira como nós raciocinamos quando queremos (informalmente) provar um argumento.

Prova n n Dados H uma fórmula e b um conjunto de fórmulas (hipóteses) Uma prova de H a partir de b é uma derivação onde n n As regras de inferência são aplicadas tendo como premissas fórmulas de b A última fórmula da derivação é H

Regras de inferência conjunção n Eliminação da conjunção (^E): n n H^G H G Sócrates e Platão eram gregos; logo, Sócrates era grego

Regras de inferência conjunção n Introdução da conjunção (^I): n n H H^G G -> derivação Platão era grego; Aristóteles era grego; logo, Platão e Aristóteles eram gregos

Exemplo de prova n n n P ^ Q, R |- Q ^ R P^Q (Premissa) Q (^E) R (Premissa) Q^R (^I) Exercícios: n n n (P^Q) ^ R, S^T |- Q^S P^Q |- Q^P (P^Q) ^ R |- P ^ (Q^R)

Regras da Dedução Natural implicação n Eliminação da implicação ( E) n n H H G G Se Deus existe, a vida é sagrada; Deus existe, logo, a vida é sagrada

Regras da Dedução Natural implicação n Introdução da implicação ( I) n n n [H] (hipótese eliminada) | G. H G A neve é branca; logo, tem cor. Se a neve é branca, tem cor.

Exemplo de eliminação da implicação n n P^Q, (P (Q R)) ├ (Q R) P^Q P (^E) P (Q R) (premissa) (Q R) ( E)

Exemplo de introdução da implicação n n n ├ (P ((P Q) Q) Supor os antecedentes Eles não poderão ser usados depois [(P Q)] (hipóteses) Q ( E) (P Q) Q) ( I) (P ((P Q) Q) ( I) n [P]

Exercício ├ (P (Q P)) n ├ (P (Q R)) ((P^Q) R)) n

Exercícios n n n 1. { P^Q, ( P^Q) (R^ P)} |- R^ P 2. {P (Q R), P Q, P} |- R 3. {P (P Q), P} |- Q

Regras da Dedução Natural - disjunção n Introdução da disjunção (v. I) n n H Hv. G G. Hv. G Um ser é um Homem se, e só se, for racional; logo, se um ser for um Homem, é racional, e se for racional, é um Homem

Regras da Dedução Natural - disjunção n Eliminação da disjunção (v. E) n Hv. G n [H] D 1 E [G] (hipóteses) D 2 E E Ou Deus existe, ou não existe. Se existe, não se pode torturar crianças por prazer. Mas se não existe, não se pode igualmente torturar crianças por prazer. Logo, em qualquer caso, não se pode torturar crianças por prazer.

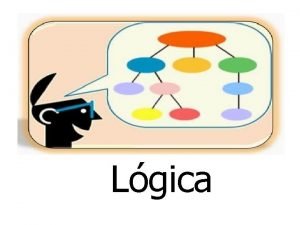
Exemplo de Eliminação da disjunção n {Pv. Q, Q, P} |- false n [P] Pv. Q. P (prem. ) [Q] Q (prem. ) false

Regras da Dedução Natural - negação n n n De uma derivação de uma contradição (false) a partir de uma hipótese H, pode-se descartar a hipótese e inferir H e vice-versa [H] ( I) | false H [ H] | false H Exercícios: H H e H H ( E ou RAA) reductio ad absurdum

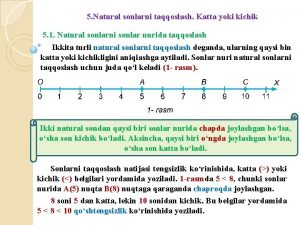
Regras da Dedução Natural - negação n n n Reductio ad Absurdum [H] ( I) | B^ B A Quem não tem deveres não tem direitos; os bebés não têm deveres; logo, não têm direitos; mas os bebés têm direitos; logo, é falso quem não tem deveres não tem direitos

Exercício n n Mostre que o seguintes argumento é válido: Se este argumento for incorreto e válido, então nem todas as suas premissas são verdadeiras. Todas as suas premissas são verdadeiras. Ele é válido. Portanto ele é correto.

Solução n Identificando as Sentenças: n n P: as premissas deste argumento são verdadeiras. S: este argumento é correto. V: este argumento é válido. Formalizando: {( S ^ V) P, P, V} ├ S

Exercício n Deus não existe. Pois, se Deus existisse a vida teria significado. Mas a vida não tem significado. Prove isso!

Quando tudo o mais falhar n n n EFQ: ex falso quodlibet ou regra da contradição Podemos estar loucos, então qualquer literal é aceitável! false H

Prova de EFQ {P, P} ├ Q n Q. P P (prem. ) false Q ( E) n

Exemplo n Prove o Silogismo Disjuntivo, usando EFQ: {P v Q, P} ├ Q

Lógicas clássicas n n Lógica minimal: {^v } x {IE} Lógica intuicionista = Lógica minimal U EFQ

Exercícios n n n { P (Q R), P, Q} |= R { P Q, P} |= Q {P (Q ^ R), P} |= P ^ Q {(P ^ Q) (R ^ S), P, Q} |= S { A B, C (Dv. E), D C, A E} |= (C B) {Cv(B A), A R, (B R) S} |= ( C S)