Tema 2 EL LENGUAJE DE LA LGICA PROPOSICIONAL



















































- Slides: 51

Tema 2. EL LENGUAJE DE LA LÓGICA PROPOSICIONAL a) La construcción de fórmulas bien formadas

Cuando el lenguaje falla… Una oración puede ser defectuosa a 3 niveles: 1. SINTÁCTICO A esta oración del castellano les falla algo A este otra oración le fallar todavía más cosa Última es esta galimatías un oración puro

Cuando el lenguaje falla… Una oración puede ser defectuosa a 3 niveles: 2. SEMÁNTICO Esta pitufa del castellano tiene una palabra extraña Las ideas verdes incoloras duermen furiosamente Confucio es impar La existencia es el devenir del karma cuántico

Cuando el lenguaje falla… Una oración puede ser defectuosa a 3 niveles: 3. PRAGMÁTICO Él ha dicho que le dé la medicina “Declaro abierta la sesión” (dicho por un conserje del Parlamento) ¿Me da un libro sobre cómo hacer amigos, carahuevo?

3 niveles de análisis del lenguaje 1. SINTAXIS: Centrada en la estructura formal de las oraciones 2. SEMÁNTICA: Centrada en las condiciones de verdad de las oraciones 3. PRAGMÁTICA: Centrada en los efectos del contexto sobre las oraciones

3 niveles de análisis del lenguaje • • En lógica sólo nos va a interesar la sintaxis y la semántica. Dentro de la semántica sólo nos va a interesar la parte formal, i. e. , el modo en que la disposición formal de los elementos afecta a los valores de verdad: Sólo Kant ama a Hume ≠ Kant ama sólo a Hume

El alfabeto lógico • Todo lenguaje necesita de: 1. Un alfabeto, i. e. , un conjunto de elementos primitivos desde los que construimos sus expresiones • El alfabeto latino no resulta ser el mismo que el ruso

La sintaxis lógica • Todo lenguaje necesita de: 2. Reglas de combinación de los elementos primitivos • Inglés y español comparten alfabeto, pero no admiten las mismas combinaciones: ortográficas: THR no es una combinación de letras admisible en español sintácticas: el español admite sujeto elíptico

Alfabeto de la lógica proposicional • El lenguaje de la lógica proposicional (L 0) necesita tres tipos distintos de símbolos: 1. CONSTANTES PROPOSICIONALES 2. CONECTIVAS LÓGICAS 3. SÍMBOLOS AUXILIARES

Alfabeto de la lógica proposicional 1. CONSTANTES PROPOSICIONALES - Simbolizan oraciones o proposiciones, i. e. , unidades que tienen un valor de verdad - Son los equivalentes lógicos de ‘llueve’, ‘yo soy Pepe’, ‘mañana es viernes’, ‘el universo es una sucesión infinita de transmigraciones cósmicas’

Alfabeto de la lógica proposicional 1. CONSTANTES PROPOSICIONALES - Utilizaremos las siguientes letras minúsculas: p, q, r, s, t, u - Si necesitamos simbolizar más oraciones (un número infinito de ellas), recurrimos a subíndices numéricos: p 1, p 2, p 3, p 4, p 5 …

Alfabeto de la lógica proposicional 2. CONECTIVAS LÓGICAS - Las oraciones pueden conectarse entre sí por medio de partículas con valor lógico - Las principales partículas son cinco, que equivalen a las siguientes: Y, O, SI…(ENTONCES), SI Y SÓLO SI, NO

Alfabeto de la lógica proposicional 2. CONECTIVAS LÓGICAS - Estas partículas caen en dos grupos: a) Binarias: Las que conectan dos oraciones: Hume canta Y Kant humea Platón tiene razón O la tiene Aristóteles SI Dios no existe, todo está permitido Aprobaré lógica SI Y SÓLO SI estudio

Alfabeto de la lógica proposicional 2. CONECTIVAS LÓGICAS b) Monarias: Las que se aplican a una sola oración: Hume NO canta NO hay vida más allá de Marte NO todos los filósofos están locos (ojo! No confundir con: Los filosófos NO están locos)

Alfabeto de la lógica proposicional 2. CONECTIVAS LÓGICAS - En lógica estas partículas reciben nombres y símbolos especiales: No = NEGADOR ¬

Alfabeto de la lógica proposicional 2. CONECTIVAS LÓGICAS - En lógica estas partículas reciben nombres y símbolos especiales: Y = CONYUNTOR

Alfabeto de la lógica proposicional 2. CONECTIVAS LÓGICAS - En lógica estas partículas reciben nombres y símbolos especiales: O = DISYUNTOR

Alfabeto de la lógica proposicional 2. CONECTIVAS LÓGICAS - En lógica estas partículas reciben nombres y símbolos especiales: SI…(ENTONCES) = CONDICIONAL

Alfabeto de la lógica proposicional 2. CONECTIVAS LÓGICAS - En lógica estas partículas reciben nombres y símbolos especiales: SI Y SÓLO SI = BICONDICIONAL

Alfabeto de la lógica proposicional 3. SÍMBOLOS AUXILIARES - Son paréntesis y corchetes, que sirven para agrupar los otros símbolos de manera que se puedan evitar ambigüedades: ( ) [ ]

Alfabeto de la lógica proposicional He aquí todo de una vez: CONSTANTES: p, q, r, s, t, u, p 1, p 2, p 3 … CONECTIVAS: ¬, , AUXILIARES: (, ), [, ]

Recursividad • La mayoría de los lenguajes son recursivos: empleando un número finito de elementos es posible construir un número infinito de oraciones. La mosca a la que persigue la araña a la que persigue el ratón al que persigue el gato al que persigue el perro es de color negro

Recursividad • Una fuente de recursividad es la posibilidad de unir oraciones simples para formar compuestas. • Las partículas lógicas desempeñan en esto un papel fundamental.

Recursividad • La recursividad comienza por tomar algunos elementos básicos y definir cómo se construyen los elementos complejos a partir de ellos: - Dadas las oraciones básicas ‘Hume canta’, ‘Kant baila’, también son oraciones las siguientes: Hume canta y Kant baila Hume canta o Kant baila Si Hume canta, Kant baila Hume no canta Kant no baila Hume canta si y sólo si Kant baila ETC.

Recursividad • Podemos seguir aplicando esto en general: dadas las oraciones O y O’, son también oraciones las siguientes: O y O’, O o O’, Si O entonces O’, no O, etc. • Podemos aplicar la regla cuantas veces queramos: dado que • ‘Hume canta y Kant baila’ y ‘Hegel da palmas’ son oraciones, también lo será • ‘Si Hume canta y Kant baila, Hegel da palmas’

Recursividad -Hume canta o Kant baila o Hegel da palmas -Hume canta y Kant baila y Hegel da palmas -Hume canta, o Kant baila y Hegel da palmas -Hume canta o Kant baila, y Hegel da palmas -Si Hume canta y Hegel da palmas, Kant baila -Hegel da palmas si y sólo si Kant baila -Si Hume canta, entonces si Kant baila, Hegel da palmas

Recursividad • La recursividad permite construir algunas oraciones peculiares: -Hume canta y Kant baila y Hume canta y Kant baila… -Si Hegel da palmas, Hegel da palmas -Hume canta o Hume canta o Hume canta o Hume canta Son peculiares desde el punto de vista pragmático, pero sintáctica y semánticamente están bien construidas

Recursividad • Nuestro lenguaje lógico también va a ser recursivo. • Las oraciones en nuestro lenguaje se van a llamar FÓRMULAS • Comenzaremos por definir cuáles son las oraciones simples o fórmulas atómicas • A continuación daremos un método de combinación de fórmulas atómicas para obtener oraciones compuestas o fórmulas moleculares

Fórmulas atómicas • Serán las que correspondan a las oraciones simples del castellano: sin ninguna partícula lógica. • Se trata por tanto de las constantes proposicionales: p son (algunas) fórmulas atómicas q r …

Fórmulas moleculares • Las formaremos a partir de las atómicas, empleando las conectivas lógicas: p q p r son (algunas) fórmulas moleculares q p r q q

Ambigüedad • En el lenguaje natural con frecuencia aparecen posibles ambigüedades: Hume canta o Kant baila y Hegel da palmas ¿Da o no da palmas Hegel? Ahora sí: Hume canta o Kant baila, y Hegel da palmas Ahora no se sabe: Hume canta, o Kant baila y Hegel da palmas

Ambigüedad • En lógica queremos construir fórmulas que excluyan toda ambigüedad. • En el lenguaje natural usamos diversos elementos para evitar la ambigüedad, como: 1) pausas prosódicas, 2) signos de puntuación y, 3) el contexto. • Pero en lógica sólo tenemos un recurso (parecido a 2): construir las fórmulas con reglas muy precisas.

Ambigüedad - Nuestro principal recurso contra la ambigüedad son los PARÉNTESIS. - Sea: p Hume canta ; q Kant baila; r Hegel da palmas p q r es AMBIGUA; equivale a: Hume canta o Kant baila y Hegel da palmas p (q r) H canta, o K baila y He da palmas (p q) r H canta o K baila, y He da palmas

Metavariables - Si la lógica es nuestro lenguaje objeto, el castellano es su metalenguaje. - Pero necesitamos ampliar nuestro metalenguaje con algunos símbolos que hacen las veces de abreviaturas. - Para referirnos a fórmulas en general usaremos letras griegas: … - Las llamaremos METAVARIABLES

Metavariables - Una constante, como p, representa aquello que la hace verdadera o falsa (llueve; las rosas son rojas, etc) - Una metavariable, como , representa cualquier fórmula: p ; ¬q ; p r ; p (q r) ; p (p p) … - Vamos a definir nuestras reglas de formación de fórmulas de manera más precisa

Reglas de formación • (i) Toda constante proposicional sola es una fórmula (atómica) • (ii) Si es fórmula, entonces ¬ es fórmula • (iii) Si , son fórmulas, ( ), ( ) son fórmulas • (iv) Sólo son fórmulas secuencias que satisfacen (i), (ii) o (iii)

Reglas de formación (i) Toda constante proposicional sola es una fórmula - De este modo obtenemos nuestras fórmulas atómicas: p q r s t u p 1 p 2 p 3 …

Reglas de formación (ii) Si es fórmula, entonces ¬ es fórmula - Dadas las anteriores, también son fórmulas: ¬p ¬q ¬r ¬s ¬t ¬u ¬p 1 ¬p 2 ¬p 3 … -Podemos aplicar recursivamente (ii) sobre las fórmulas recién obtenidas: ¬¬p ¬¬q … ¬¬¬p Todas estas también son fórmulas

Reglas de formación (iii) Si , son fórmulas, ( ), ( ) son fórmulas -Dadas (i) y (iii) serán fórmulas: (p q) (p s) (p r) … (q p ) … (p q) (p s) (p r) … (q p) … (p q) (p r) …

Reglas de formación (iii) Si , son fórmulas, ( ), ( ) son fórmulas -Si además tenemos en cuenta (ii), son fórmulas: (p ¬q) (¬p s) (p ¬r) … (q ¬p ) … (¬p q) (p ¬s) (¬p ¬r) … (¬q p) … (p ¬q) (¬p r) (¬p ¬r) … (¬p q) (p ¬r) (¬p r) …

Reglas de formación (iii) Si , son fórmulas, ( ), ( ) son fórmulas -Y podemos aplicar otra vez (ii) sobre las últimas fórmulas : ¬(p ¬q) ¬(¬p s) ¬(p ¬r) … ¬(q ¬p ) … ¬(¬p q) ¬(p ¬s) ¬(¬p ¬r) …¬ (¬q p) … ¬(p ¬q) ¬(¬p r) ¬(¬p ¬r) … ¬(¬p q) ¬(p ¬r) ¬(¬p r) … ¬¬(p q) … ¬¬(¬p ¬q) … ¬(p ¬¬q) …

Reglas de formación - Y podemos seguir aplicando (ii) y (iii) cuanto queramos: (p q)) (¬p (q ¬s)) (p ¬r) (q ¬p ) (p ((¬p q) (p ¬s))) ((¬p ¬r) (¬q p)) (p ¬q) …

Reglas de formación (iv) Sólo son fórmulas secuencias que satisfacen (i), (ii) o (iii) - Esta es una cláusula de cierre, que limita nuestras fórmulas exclusivamente a las formadas por las reglas anteriores.

Reglas de simplificación • Pueden suprimirse siempre: (a) Los dos paréntesis externos: (p (q ¬r)) p (q ¬r) (Nota: El símbolo se lee como ‘es equivalente a’)

Reglas de simplificación • Pueden suprimirse siempre: (b) Los paréntesis internos no precedidos de negador en secuencias compuestas totalmente por conyuntores o totalmente por disyuntores: (p (q r)) (p q r) pero (p ¬(q r)) (p ¬q r) !! (p (¬q r)) (p ¬q r) pero (p ¬(q r)) (p ¬q r) !!

Conectiva dominante • Consideremos cómo se forman las fórmulas moleculares: - La última regla de formación que hayamos usado ha tenido que ser (ii) o (iii), i. e. , la última regla ha introducido el negador o una conectiva binaria: ¬p lo último introducido es el negador ¬ q ¬r lo último introducido es el conyuntor p (q r) lo último introducido es el disyuntor ¬(p q) (¬p ¬q) lo último introducido es

Conectiva dominante • La última conectiva introducida será la CONECTIVA DOMINANTE de la fórmula. • Es importante distinguirla, porque es a la que habrá que atender para determinar el valor de verdad de la fórmula. p (r s) ¬(p (q r)) ¬p (p p)) ¬((p q) ¬(p q)) (((p q) p) q) p ¬(p ¬(q r ¬(p q))) ¬ el primer ¬ el segundo no es fórmula


Ejercicio: ¿cuáles son fórmulas? ((¬q r) ¬(p q)) ¬(q r) ((p ¬q) q) NO ¬(p ¬q) ¬r) ¬s) t)))) NO (((p q ¬r) (¬q ¬p)) (p ¬s)) (¬p q r) SÍ (p (q ¬p r)) (p q) NO (((p (q ¬r)) (¬q s)) (s ¬p)) (p q) NO (p q ¬r) (p ¬q ¬r) (¬p q r) SÍ (p q) (¬p q) (p ¬q) (¬p ¬q) SÍ

Ejercicio: conectiva dominante el primer ¬ ¬(p ¬q) (p q) (¬p q) ((q (r ¬s)) (¬¬p q)) ¬r ¬(s (p q)) ¬ ¬(p (¬q ¬(r (¬s t)))) el primer ¬ ¬¬¬¬¬¬¬¬¬p el primer ¬ (¬q (r (¬p q))) (q (¬r (p ¬q))) 2º

Ejercicio: conectiva dominante (((¬q r) ¬(p q)) ¬(q r)) ((p ¬q) q) 2º ¬((((p ¬q) ¬r) ¬s) t) el primer ¬ (((p q ¬r) (¬q ¬p)) (p ¬s)) (¬p q r) 2º (p (q (¬p r))) (p q) (((p (q ¬r)) (¬q s)) (s ¬p)) (p q) 3 er (p q ¬r) (p ¬q ¬r) (¬p q r) cualquier (p q) (¬p q) (p ¬q) (¬p ¬q) cualquier
 Simbolo de pero en logica proposicional
Simbolo de pero en logica proposicional Lenguaje proposicional
Lenguaje proposicional Que es un argumento
Que es un argumento Lgica
Lgica Lgica
Lgica Metodo condicional asociado
Metodo condicional asociado Lgica
Lgica Lgica
Lgica Lgica
Lgica Lgica
Lgica Implicaciones tautologicas
Implicaciones tautologicas Tabla de proposiciones
Tabla de proposiciones Taller de logica proposicional
Taller de logica proposicional Contigencia logica
Contigencia logica Que es una tautologia
Que es una tautologia Enunciado no proposicional ejemplos
Enunciado no proposicional ejemplos Proposicion categorica
Proposicion categorica üuma
üuma Proposiciones
Proposiciones Si
Si Tollendo tollens
Tollendo tollens La tabla de verdad de la conjunción
La tabla de verdad de la conjunción Qué tipos de entrevista hay
Qué tipos de entrevista hay Naturalisme seniman
Naturalisme seniman Tema-tema teologi perjanjian lama
Tema-tema teologi perjanjian lama Ejemplos de delimitación del problema
Ejemplos de delimitación del problema El tema y sub tema
El tema y sub tema Comunicacin escrita
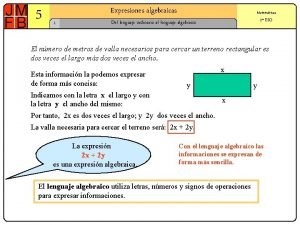
Comunicacin escrita Lenguaje de ecuaciones
Lenguaje de ecuaciones Lenguaje algebraico 2 eso
Lenguaje algebraico 2 eso Lenguaje algebraico ejemplos
Lenguaje algebraico ejemplos Lenguaje verbal a lenguaje algebraico
Lenguaje verbal a lenguaje algebraico Dibujos para niños de pentecostes
Dibujos para niños de pentecostes Pendekatan bertema bahasa melayu
Pendekatan bertema bahasa melayu Tema pengembangan kurikulum 2013
Tema pengembangan kurikulum 2013 Dozpívav
Dozpívav Punim diplome usht
Punim diplome usht Blues pro bláznivou holku rozbor
Blues pro bláznivou holku rozbor Rezumat florin scrie un roman
Rezumat florin scrie un roman Nastavna tema
Nastavna tema Runtime error 7 out of memory
Runtime error 7 out of memory Uri nang talumpati
Uri nang talumpati Khotbah ibadah kaum bapak
Khotbah ibadah kaum bapak Conclusion sobre un tema
Conclusion sobre un tema Tema windows 10
Tema windows 10 Que tema es?
Que tema es? Tema 6
Tema 6 Marcel bajka
Marcel bajka Projekt lendor
Projekt lendor Tema marketing
Tema marketing Partes de un ensayo
Partes de un ensayo Q es un ensayo
Q es un ensayo