LESSON 9 4 Polar Forms of Conic Sections

LESSON 9– 4 Polar Forms of Conic Sections

Five-Minute Check (over Chapter 9 -3) Then/Now Concept Summary: Eccentricities of Conics Key Concept: Polar Equations of Conics Example 1: Identify Conics from Polar Equations Example 2: Write Polar Equations of Conics Example 3: Write the Polar Form of Conics in Rectangular Form

Over Lesson 9 -3 Find rectangular coordinates for the point with the given polar coordinates. A. B. C. D. (0, 3)

Over Lesson 9 -3 Find rectangular coordinates for the point B(10, 52°) with the given polar coordinates. A. (9. 84, 10. 99) B. (10. 62, 10. 79) C. (6. 16, 7. 88) D. (– 1. 63, 9. 87)

Over Lesson 9 -3 Find two pairs of polar coordinates for C(– 2, 5) if 0 ≤ θ ≤ 2π. A. (4. 58, 111. 80), (4. 58, 291. 80) B. (4. 58, – 0. 38), (4. 58, 5. 90) C. (5. 39, – 1. 19), (5. 39, 1. 19) D. (5. 39, 1. 95), (– 5. 39, 5. 09)

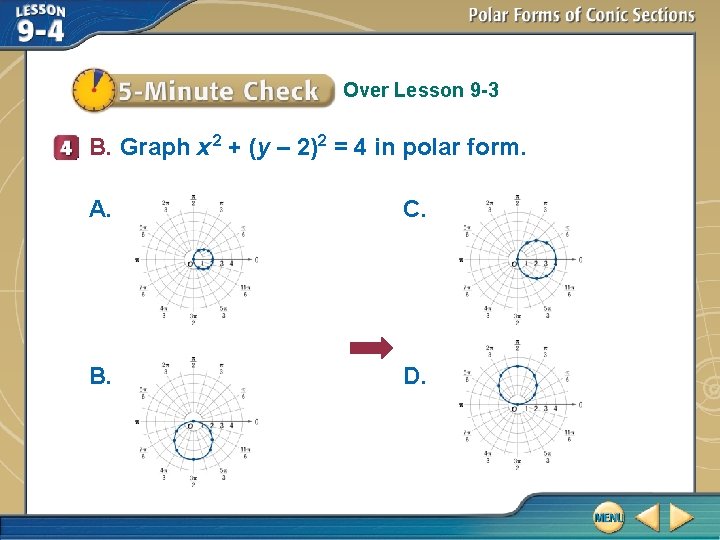
Over Lesson 9 -3 A. Identify the graph of x 2 + (y – 2)2 = 4. Then write the equation in polar form. A. circle with center at (0, 2) and radius of 2; r = 4 sin B. circle with center at (0, – 2) and radius 2; r = – 4 sin C. circle with center at (2, 0) and radius 2; r = 4 cos D. circle with center at (0, 2) and radius 2; r = 2 cos

Over Lesson 9 -3 B. Graph x 2 + (y – 2)2 = 4 in polar form. A. C. B. D.

Over Lesson 9 -3 Which of the following is the rectangular form of r = 4 csc θ ? A. y = 4 B. x 2 + y 2 = 4 C. x = 4 D. y = 4 x

You defined conic sections. (Lessons 7 -1 through 7 -3) • Identify polar equations of conics. • Write and graph the polar equation of a conic given its eccentricity and the equation of its directrix.

Identify Conics from Polar Equations A. Determine the eccentricity, type of conic, and equation of the directrix for . Write the equation in standard form, Original equation

Identify Conics from Polar Equations Factor the numerator and denominator. Divide the numerator and denominator by 3.

Identify Conics from Polar Equations In this form, you can see from the denominator that e= . Therefore, the conic is an ellipse. For polar equations of this form, the equation of the directrix is x = d. From the numerator, we know that ed = d= or 5. Therefore, the equation of the directrix is x = 5. Answer: , so ellipse; x = 5

Identify Conics from Polar Equations Check Sketch the graph of and its directrix x = 5 using either the techniques shown in Lesson 9 -2 or a graphing calculator. The graph is an ellipse with its directrix to the right of the pole.

Identify Conics from Polar Equations B. Determine the eccentricity, type of conic, and equation of the directrix for . Write the equation in standard form. Original equation Factor the numerator and denominator.

Identify Conics from Polar Equations Divide the numerator and denominator by – 3. The equation is of the form , so e = 2. Therefore, the conic is a hyperbola. For polar equations of this form, the equation of the directrix is y = –d. Because ed = 5, d = 5 ÷ 2 or 2. 5. Therefore, the equation of the directrix is y = – 2. 5. Answer: e = 2; hyperbola; y = – 2. 5

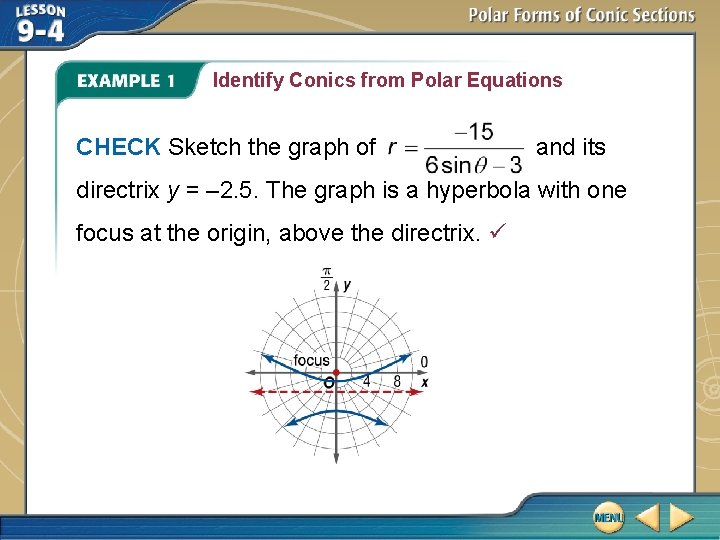
Identify Conics from Polar Equations CHECK Sketch the graph of and its directrix y = – 2. 5. The graph is a hyperbola with one focus at the origin, above the directrix.

Determine the eccentricity, type of conic, and equation of the directrix for A. e = 0. 5; ellipse; y = 12 B. e = 1; parabola; x = 6 C. e = 2; hyperbola; x = – 6 D. e = 0. 5; ellipse; y = 6

Write Polar Equations of Conics A. Write and graph a polar equation and directrix for the conic with e = 2 and directrix y = 3. Because e = 2, the conic is a hyperbola. The directrix, y = 3, is above the pole, so the equation is of the form Use the values for e and d to write the equation. Polar form of conic with directrix y = d e = 2 and d = 3

Write Polar Equations of Conics Sketch the graph of this polar equation and its directrix. The graph is a hyperbola with its directrix above the pole. Answer: hyperbola;

Write Polar Equations of Conics B. Write and graph a polar equation and directrix for the conic with e = 0 and vertices at (– 2, 0) and (4, 0). Because e = , the conic is an ellipse. The center of the ellipse is at (1, 0), the midpoint of the segment between the given vertices. This point is to the right of the pole. Therefore, the directrix will be to the left of the pole at x = –d. The polar equation of a conic with this directrix is

Write Polar Equations of Conics Use the value of e and the polar form of a point on the conic to find the value of d. The vertex point (4, 0) has polar coordinates or (4, 0). Polar form of conic with directrix x = –d e= , r = 4, and = 0

Write Polar Equations of Conics cos 0 = 1 Simplify. Therefore, the equation for the ellipse is Because d = 8, the equation of the directrix is x = – 8. The graph is an ellipse with vertices at (– 2, 0) and (4, 0).

Write Polar Equations of Conics Answer: ellipse;

Write a polar equation for the conic with e = 0. 2 and vertices at (– 4, 0) and (6, 0). A. B. C. D.

Write the Polar Form of Conics in Rectangular Form A. Write in rectangular form. Step 1 Analyze the polar equation. For this equation, e = 1 and d = 6. The eccentricity and form of the equation determine that this is a parabola that opens vertically with focus at the pole and a directrix y = – 6. The general equation of such a parabola in rectangular form is (x – h)2 = 4 p(y – k).

Write the Polar Form of Conics in Rectangular Form Step 2 Determine values for h, k, and p. The vertex lies between the focus F and directrix of the parabola, occurring when as shown in the figure. Evaluating the function at this value, we find that the vertex lies at polar coordinates which correspond to rectangular coordinates (0, – 3). So, (h, k) = (0, – 3). The distance p from the vertex at (0, – 3) to the focus at (0, 0) is 3.

Write the Polar Form of Conics in Rectangular Form Step 3 Substitute the values for h, k, and p into the standard form of an equation for a parabola. (x – h)2 = 4 p(y – k) Standard form of a parabola (x – 0)2 = 4(3)[y – (– 3)] h = 0, k = – 3, and p = 3 x 2 = 12 y + 36 Simplify. Answer: x 2 = 12 y + 36

Write the Polar Form of Conics in Rectangular Form B. Write Step 1 in rectangular form. Analyze the polar equation. For this equation, e = 0. 8 and d = 2. 25. The eccentricity and form of the equation determine that this is an ellipse with directrix x = – 2. 25. Therefore, the major axis of the ellipse lies along the polar or x-axis. The general equation of such an ellipse in rectangular form is

Write the Polar Form of Conics in Rectangular Form Step 2 Determine values for h, k, a, and b. The vertices are the endpoints of the major axis and occur when = 0 and π as shown in the figure. Evaluating the function at these values, we find that the vertices have polar coordinates (9, 0) and (1, π), which correspond to rectangular coordinates (9, 0) and (– 1, 0). The ellipse's center is the midpoint of the segment between the vertices, so (h, k) = (4, 0).

Write the Polar Form of Conics in Rectangular Form The distance a between the center and each vertex is 5. The distance c from the center to the focus at (0, 0) is 4. By the Pythagorean relation Step 3 Substitute the values for h, k, a, and b into the standard form of an equation for an ellipse. Standard form of an ellipse h = 4, k = 0, a = 5, and b = 3

Write the Polar Form of Conics in Rectangular Form Simplify. Answer:

Write the polar equation form. A. B. C. D. in rectangular

LESSON 9– 4 Polar Forms of Conic Sections