The Conic Sections Chapter 10 Introduction to Conic

Introduction to Conic Sections (10. 1) 4 A conic section is the intersection of

How are these sections created? By changing the angle and the location of the

Circle (Section 10. 2) 4 When a plane intersects a double-napped cone and is

Ellipse (Section 10. 3) 4 When a plane intersects a doublenapped cone and is

Hyperbola (Section 10. 4) 4 When a plane intersects a doublenapped cone and is

Parabola (Section 10. 5) 4 When a plane intersects a doublenapped cone and is

Foundational Knowledge – Chapter 10 The Distance Formula Example: find the distance between the

Foundational Knowledge • The Midpoint Formula (The midpoint is the average of the two

Putting it all together: the parallelogram example Example: Using a combination of these two

( -2, 3) (-3, -2) (2, -3) (3, 2) Compare slope and length of

Slides: 11

Download presentation

The Conic Sections Chapter 10

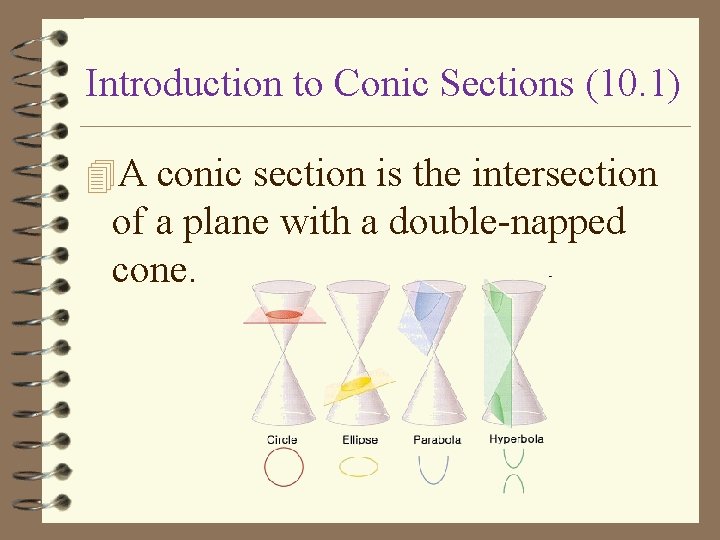
Introduction to Conic Sections (10. 1) 4 A conic section is the intersection of a plane with a double-napped cone.

How are these sections created? By changing the angle and the location of the intersection, a parabola, circle, ellipse or hyperbola is produced.

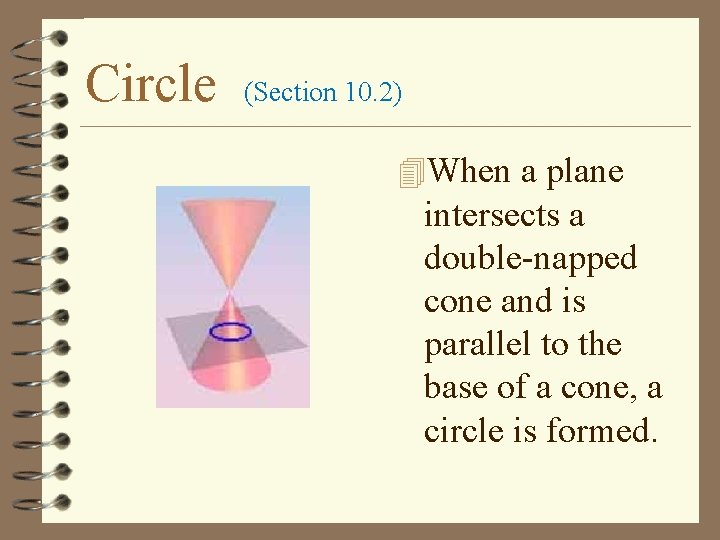
Circle (Section 10. 2) 4 When a plane intersects a double-napped cone and is parallel to the base of a cone, a circle is formed.

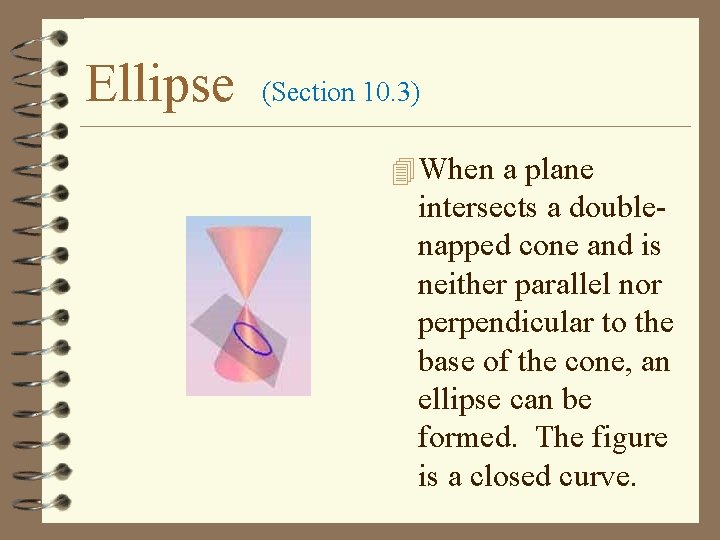
Ellipse (Section 10. 3) 4 When a plane intersects a doublenapped cone and is neither parallel nor perpendicular to the base of the cone, an ellipse can be formed. The figure is a closed curve.

Hyperbola (Section 10. 4) 4 When a plane intersects a doublenapped cone and is neither parallel or perpendicular to the base of the cone, a hyperbola can be formed. The figure consists of two open curves.

Parabola (Section 10. 5) 4 When a plane intersects a doublenapped cone and is parallel to the side of the cone, a parabola is formed.

Foundational Knowledge – Chapter 10 The Distance Formula Example: find the distance between the points (4, -2) and (8, 3) Answer is Remember: if the answer is not a perfect square, leave as a simplified radical expression.

Foundational Knowledge • The Midpoint Formula (The midpoint is the average of the two coordinates!) Example: Find the midpoint between (-2, 4) and (6, -5) … it’s (2, -1/2) • The Slope Formula Example: Find the slope of the two points listed above.

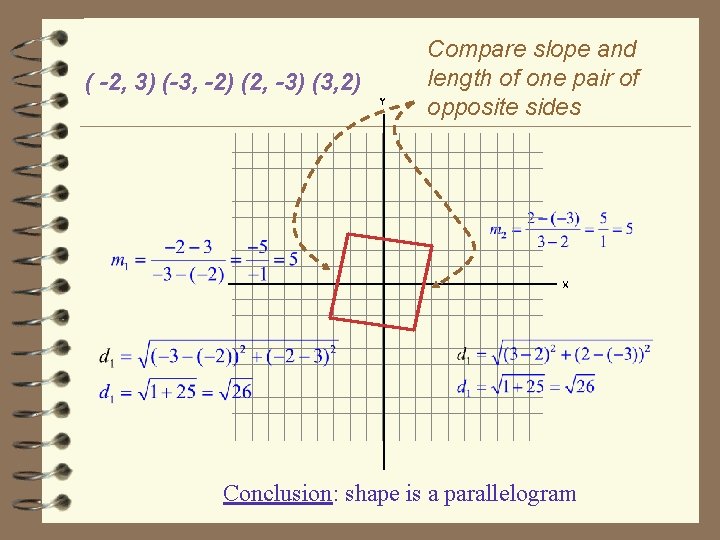
Putting it all together: the parallelogram example Example: Using a combination of these two tools, determine if the four sided shape with vertices ( -2, 3) (-3, -2) (2, -3) (3, 2) is a parallelogram. Remember: to prove a parallelogram, show that either… 4 4 One pair of opposite sides congruent (distance) and parallel (slope) or, Opposite sides are parallel (slope) or Diagonals bisect each other (midpoint) or Both pairs of opposite sides same length (distance)

( -2, 3) (-3, -2) (2, -3) (3, 2) Compare slope and length of one pair of opposite sides Conclusion: shape is a parallelogram