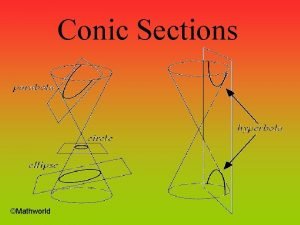
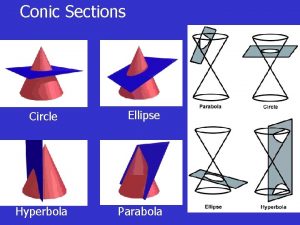
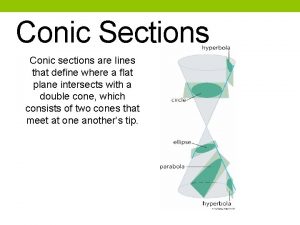
CONIC SECTIONS ELLIPSE CONIC SECTIONS ELLIPSE DEFINITION An

CONIC SECTIONS ELLIPSE

CONIC SECTIONS ELLIPSE

DEFINITION • An ellipse is define as the locus of points P(x, y) from afixed point (the focus)and the fixed line (the directric) Where PS is less than PB ( PS<PB ).

DEFINITION • An ellipse is the graph of all points the sum of whose distance from the fixed points is constant. The two fixed points are called foci.

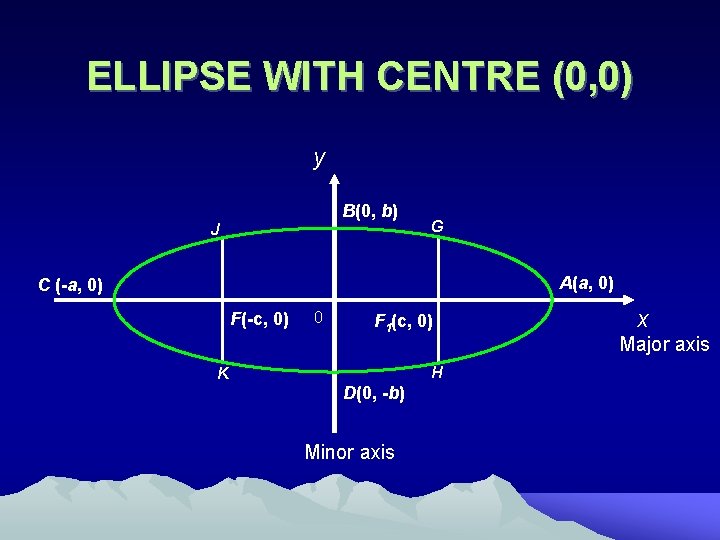
ELLIPSE WITH CENTRE (0, 0) The standard equation for an ellipse with centre ( 0, 0 ) and foci ( ± c, 0 ) is Where c 2 = a 2 - b 2 , if ( a² > b² )

ELLIPSE WITH CENTRE (0, 0) y B(0, b) J G A(a, 0) C (-a, 0) F(-c, 0) 0 F 1(c, 0) H K D(0, -b) Minor axis x Major axis

ELLIPSE WITH CENTRE (0, 0) • F and F 1 : Two fixed points on the major axis are called the foci. • AC : The longer axis of length 2 a is known as the major axis • A and C : Major vertices ( of length a from its centre ) • BC : The shorter axis of length 2 b is known as the minor axis • O : The intersection between the major axis and minor axis is the centre of ellipse. • GH and JK: A chord which passes through either focus , which is perpendicular to the major axis is known as latus rectum. (Length of latus rectum is ) GF 1=F 1 H or JF=FK : Half the length of the latus rectum is known as semi latus rectum Note: An ellipse is symmetrical with respect to its axis, Hence it has two foci, (c, 0) and -c, 0 ). An ellipse also has 2 vertices ( a, 0 ), (-a, 0) (

Example 1 Find an equation of the ellipse with vertices ( ± 4, 0 ) and foci ( ± 2, 0 ). Solution : • Since the vertices are (± 4, 0 ), we conclude that a = 4. Since the foci are ( ± 2, 0 ), • so we have c = 2. • Hence, b 2 = a 2 – c 2 = 42 – 22 = 12 and equation of the ellipse is

Example 2 Find the equation of the ellipse with centre (0, 0) with the vertices at (3, 0) and ( 0, 2 ). • The standard equation of an ellipse is • Where c 2 = a 2 – b 2 , ( a 2 > b 2 ) From the above equation a=3 and b=2. • Focus c 2 = 2 -3 • c=± = • Equation of the ellipse, • Foci : F ( , 0) ; F 1 (, 0)

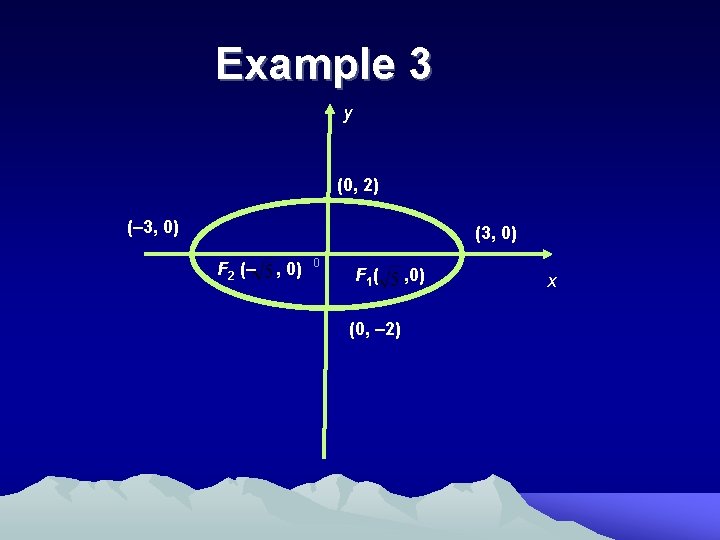
Example 3 Notes : The number under the x term is larger, the major axis is along the x -axis and the minor axis is along the y-axis. From the above equation a=3, b=2, centre (0, 0) Focus, c = ± =± Sketch the ellipse

Example 3 y (0, 2) (– 3, 0) (3, 0) F 2 (– , 0) 0 F 1 ( (0, – 2) , 0) x

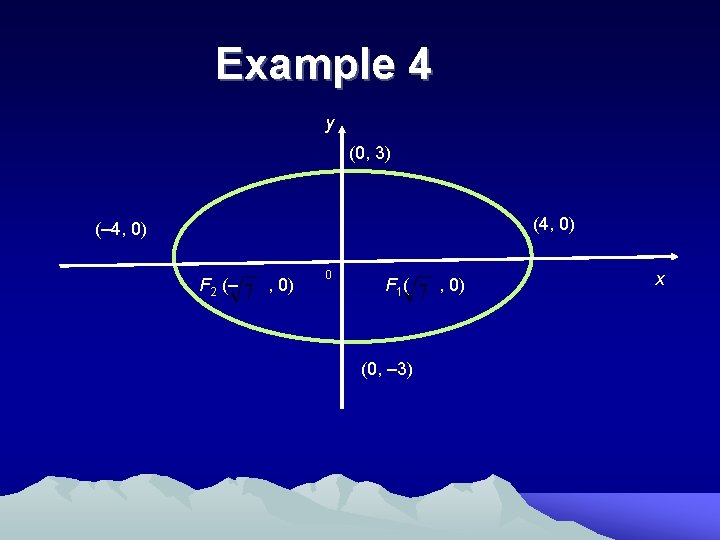
Example 4 Sketch the ellipse 9 x² + 16 y² = 144 Solution : Equation of an ellipse is for the ellipse 9 x² + 16 y² = 144 , we have (the major axis is along the xaxis )where a =4 , b =3 and c = 7 Vertices on the major axis are Foci are ( , 0), ,

Example 4 y (0, 3) (4, 0) (– 4, 0) F 2 (– , 0) 0 F 1 ( (0, – 3) , 0) x

The equation for an ellipse with centre (0, 0) and foci (0, ±C) is ( b² > a² )

Ellipse with centre ( 0, 0 ) and foci (0, ± C ) y B (0, b) G F 1 (0, c) H (–a, 0) (a, 0) A 0 F 2 (0, –c) C K J D (0, –b) X

Ellipse with centre ( 0, 0 ) and foci ( 0, ± C ) • F 1 and F 2 : Two fixed points on the major axis are called the foci. • BD : The longer axis of length 2 b is known as the major axis • B and D : Major vertices ( of length b from its centre ) • AC : The shorter axis of length 2 a is known as the minor axis • O : The intersection between the major axis and minor axis is the centre of ellipse. • GH and JK : A chord which passes through either focus , which is perpendicular to the major axis is known as latus rectum. • (Length of latus rectum is ) • GF 1=F 1 H or JF 2=F 2 K : Half the length of the latus rectum is known as semi latus rectum

Example 1 Find the equation for the ellipse that has its centre at the origin with vertices V(0, ± 7) and Foci ( 0, ± 2 ).

Solution Example 1 • • The standard equation of an ellipse is where ; • Since the vertices are ( 0, ± 7 ), we conclude that a = 7. Since the Foci are (0, ± 2), we have c = 2. • • = 22 + 72 = 4 + 49 = 53 and equation of the ellipse is

Example 2 Find the equation for the ellipse that has its centre at the origin with vertices V (0, ± 5) and minor axis of length 3. Sketch the ellipse.

Solution Example 2 • The standard equation of an ellipse is • where ; ; • Since the vertices are ( 0, ± 5 ), we conclude that b = 5. Since the minor axis is of length 3, we have • And equation of the ellipse is

Solution Example 2 Y (0, 5) 0 X (0, – 5)

Example 3 Find the focus and equation of the ellipse with centre ( 0, 0 ) vertices at ( 2, 0) and (0, 4)

Solution Example 3 The standard equation of an ellipse is where ; • From the above and ; • Equation of ellipse is • and Foci is ( 0, ) and

Example 4 Sketch the ellipse with equation :

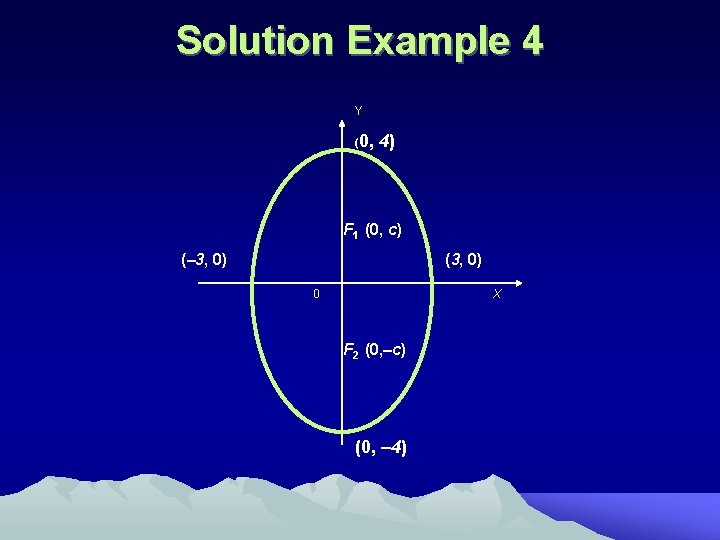
Solution Example 4 • For the ellipse we have a =3 , b =4 , therefore b² > a² • c= =± • The centre of the ellipse is ( 0, 0 ) • • The foci are ( 0, ) and ( 0, - ) The vertices : On the major axis : ( 0, 4 ) and ( 0, -4 )

Solution Example 4 Y (0, 4) F 1 (0, c) (– 3, 0) (3, 0) 0 X F 2 (0, –c) (0, – 4)

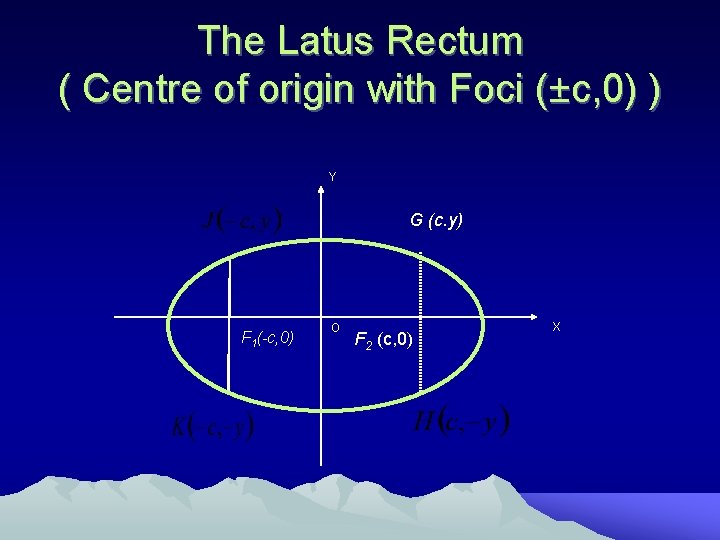
The Latus Rectum ( Centre of origin with Foci (±c, 0) ) • Definition : A chord which passes through either focus , which is perpendicular to the major axis is known as latus rectum. (Length of latus rectum is ).

The Latus Rectum ( Centre of origin with Foci (±c, 0) ) Y G (c. y) F 1(-c, 0) O F 2 (c, 0) X

The Latus Rectum ( Centre of origin with Foci (±c, 0) ) • Proof : From equation of an ellipse , , substituting • y 2 =b 2 ; from • • y 2 = b 2 y 2 = y = G (c, ), Length of GH, the latus rectum is 2 .

The Latus Rectum ( Centre of origin with Foci (±c, 0) ) Note : Length of latus rectum with centre origin with Foci (0, ± c) is 2.

Example Find the centre, vertices, foci, major and minor axes and length of the latus rectum for the ellipse :

Solution • From the equation of the ellipse ; we conclude a = 4, b = 5 , c = 3 • Centre : ( 0, 0 ) • Foci : ( 3, 0 ) and • Vertices : and ( 0, 5), Length of the major axis is 10 • Length of the minor axis is 8 • Length of latus rectum is 2 =