Polar Equations of Conics Its a whole new

Polar Equations of Conics It’s a whole new ball game in Section 8. 5 a…

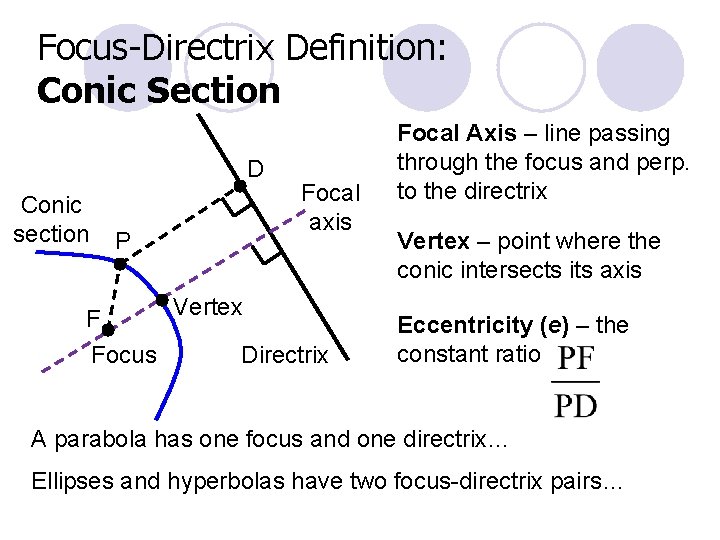
Focus-Directrix Definition: Conic Section A conic section is the set of all points in a plane whose distances from a particular point (the focus) and a particular line (the directrix) in the plane have a constant ratio. (We assume that the focus does not lie on the directrix. ) Here, we are generalizing the focus-directrix definition given for parabolas in section 8. 1 to apply to all three of our conic sections!!!

Focus-Directrix Definition: Conic Section D Conic section P Focal axis Vertex F Focus Directrix Focal Axis – line passing through the focus and perp. to the directrix Vertex – point where the conic intersects its axis Eccentricity (e) – the constant ratio A parabola has one focus and one directrix… Ellipses and hyperbolas have two focus-directrix pairs…

Focus-Directrix-Eccentricity Relationship If P is a point of a conic section, F is the conic’s focus, and D is the point of the directrix closest to P, then and where the constant e is the eccentricity of the conic. Moreover, the conic is • a hyperbola if e > 1, • a parabola if e = 1, • an ellipse if e < 1.

Writing Polar Equations for Conics Our previous definition for conics works best in combination with polar coordinates……………. . so remind me: Pole: the origin Polar Axis: the x-axis Pole Polar Axis To obtain a polar equation for a conic section, we position the pole at the conic’s focus and the polar axis along the focal axis with the directrix to the right of the pole…

Writing Polar Equations for Conics Conic section Focus at the pole Directrix We call the distance from the focus to the directrix k our previous equation becomes

Writing Polar Equations for Conics Conic section Focus at the pole Directrix Solve this for r :

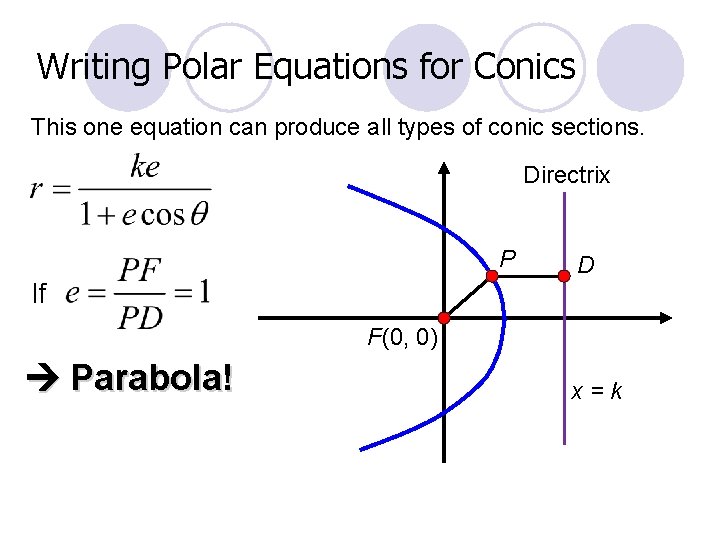
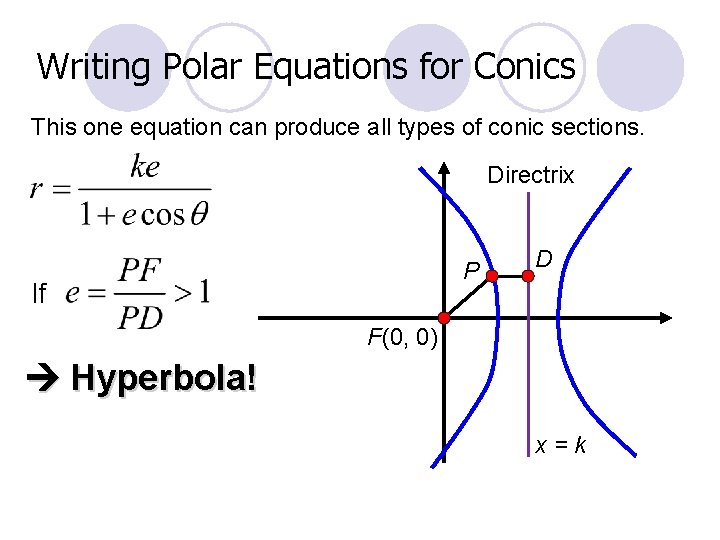
Writing Polar Equations for Conics This one equation can produce all types of conic sections. Directrix P If D F(0, 0) Ellipse! x=k

Writing Polar Equations for Conics This one equation can produce all types of conic sections. Directrix P If D F(0, 0) Parabola! x=k

Writing Polar Equations for Conics This one equation can produce all types of conic sections. Directrix P If D F(0, 0) Hyperbola! x=k

A Fun Calculator “Exploration” Set your grapher to Polar and Dot graphing modes, and to Radian mode. Using k = 3, an xy window of [– 12, 24] by [– 12, 12], 0 min = 0, 0 max = 2 , and 0 step = /48, graph for e = 0. 7, 0. 8, 1, 1. 5, 3. Identify the type of conic section obtained for each e value. Overlay the five graphs, and explain how changing the value of e affects the graph. Explain how the five graphs are similar and how they are different.

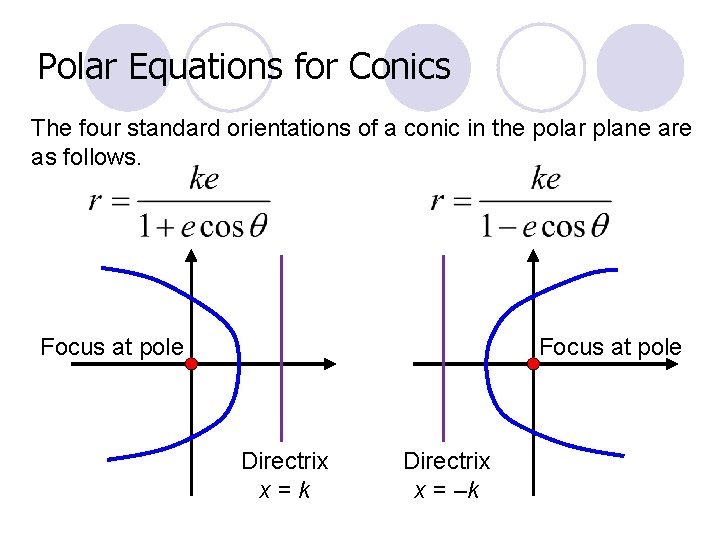
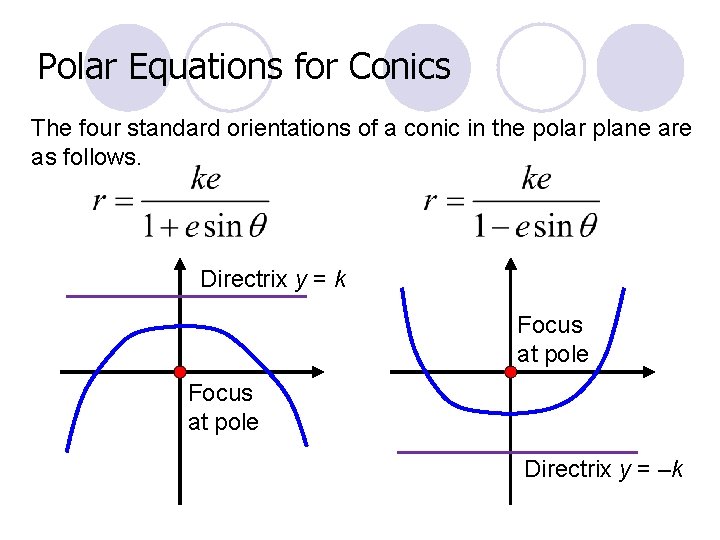
Polar Equations for Conics The four standard orientations of a conic in the polar plane are as follows. Focus at pole Directrix x=k Directrix x = –k

Polar Equations for Conics The four standard orientations of a conic in the polar plane are as follows. Directrix y = k Focus at pole Directrix y = –k

Practice Problems Given that the focus is at the pole, write a polar equation for the specified conic, and graph it. Eccentricity e = 3/5, Directrix x = 2 General Equation: Substitute in the given info: Multiply numerator and denominator by 5: Now, how do we graph this conic? ? ? (by hand by calculator)

Practice Problems Given that the focus is at the pole, write a polar equation for the specified conic, and graph it. Eccentricity e = 1, Directrix x = – 2 The graph? ? ?

Practice Problems Given that the focus is at the pole, write a polar equation for the specified conic, and graph it. Eccentricity e = 3/2, Directrix y = 4 The graph? ? ?

Practice Problems Determine the eccentricity, the type of conic, and the directrix. Divide numerator and denominator by 2: e = 1. 5 Hyperbola!!! ke = 3 k = 2 Directrix: x = 2 Verify all of this graphically? ? ?

Practice Problems Determine the eccentricity, the type of conic, and the directrix. e = 0. 75 Ellipse!!! k = 2 Directrix: y = – 2 Verify all of this graphically? ? ?