9 1 Conic Sections Conic sections curves that

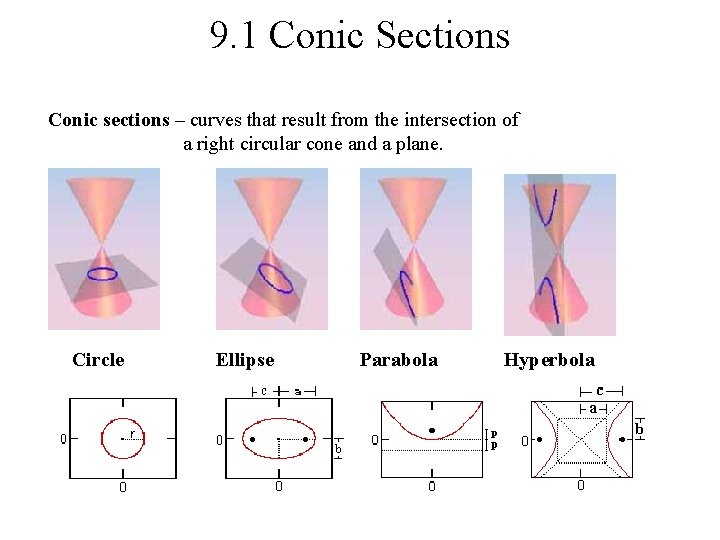
9. 1 Conic Sections Conic sections – curves that result from the intersection of a right circular cone and a plane. Circle Ellipse Parabola Hyperbola

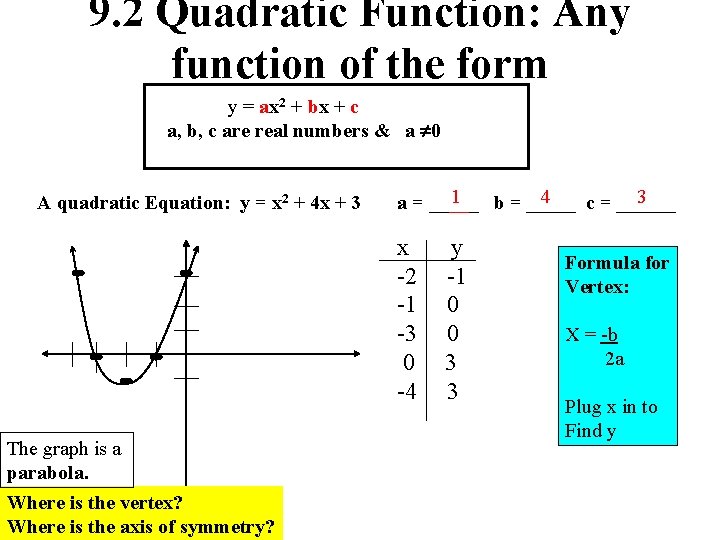
9. 2 Quadratic Function: Any function of the form y = ax 2 + bx + c a, b, c are real numbers & a 0 A quadratic Equation: y = x 2 + 4 x + 3 1 4 3 a = _____ b = _____ c = ______ x -2 -1 -3 0 -4 The graph is a parabola. Where is the vertex? Where is the axis of symmetry? y -1 0 0 3 3 Formula for Vertex: X = -b 2 a Plug x in to Find y

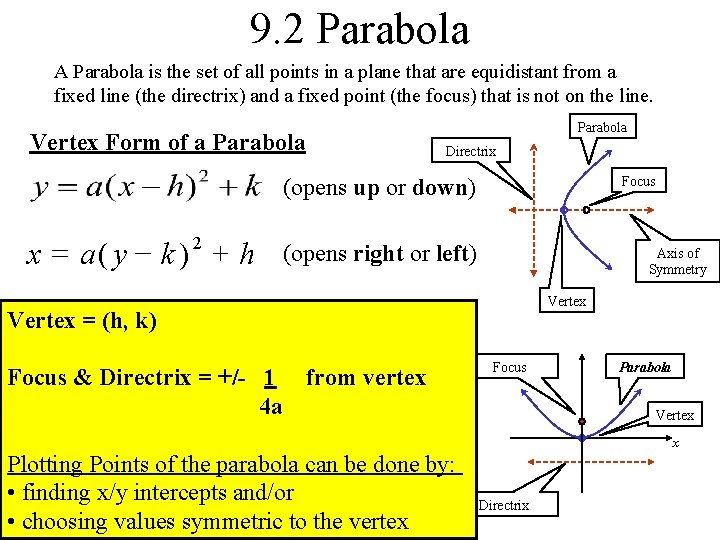
9. 2 Parabola A Parabola is the set of all points in a plane that are equidistant from a fixed line (the directrix) and a fixed point (the focus) that is not on the line. Vertex Form of a Parabola Directrix Focus (opens up or down) x = a(y - k )2 + h (opens right or left) Axis of Symmetry Vertex = (h, k) Focus & Directrix = +/- 1 from vertex 4 a Focus Parabola Vertex x Plotting Points of the parabola can be done by: • finding x/y intercepts and/or • choosing values symmetric to the vertex Directrix

Parabola Graphing Step 1: Place equation in one of two vertex forms: (opens up or down) x = a(y - k )2 + h (opens right or left) Step 2: Find the vertex at : (h, k) & determine which direction the parabola opens Step 3: Use an x/y chart to plot points symmetric to the vertex & draw the parabola Step 4: Find the focus/directrix displacement with 1/(4 a) Try the following Examples: #1) y 2 = 4 x #2) x 2 = -16 y #3) (y + 4)2 = 12(x + 2) #4) x 2 – 2 x – 4 y + 9 = 0

1. 1 Circles Standard circle equation (x – h)2 + (y – k)2 = r 2 center = (h, k) radius = r Graph the circle: (x – 2)2 + (y + 3)2 = 9 Step 1: Find the center & radius (x – 2)2 + (y – (-3))2 = 32 h is 2. Step 2: Graph the center point Step 3: Use the radius to find 4 points directly north, south, east, west of center. k is – 3. Center = (2, -3) Radius = 3 r is 3.

General Form of a Circle Equation (Changing from General to Standard Form) Standard circle equation : (x – h)2 + (y – k)2 = r 2 center = (h, k) radius = r General Form of a circle : x 2 + y 2 + Dx + Ey + F = 0 Change from General Form to Standard Form General Form: x 2 + y 2 – 4 x +6 y +4 = 0 Move constant : X’s & Y’s together : x 2 + y 2 – 4 x +6 y (x 2 – 4 x Setup to Complete Square ½ (-4) = -2 ½ (6) = 3 = -4 ) + (y 2 + 6 y ) = -4 (-2)2 = 4 Complete the Square: (x 2 – 4 x +4 ) + (y 2 + 6 y +9 )= -4 +4 +9 Factor (x – 2) + (y + 3) = 9 Standard Form (x – 2)2 + (y + 3)2 =9 (3)2 = 9

9. 3 Ellipse - the set of all points in a plane the sum of whose distances from two fixed points, is constant. These two fixed points are called the foci. The midpoint of the segment connecting the foci is the center of the ellipse. P F 1 P F 2 A circle is a special kind of ellipse. Since we know about circles, the equation of a circle can be used to help us understand the equation and graph of an ellipse.

Comparing Ellipses to Circles circle: (x – h)2 + (y – k)2 = r 2 Ellipse: (x – h)2 + (y – k)2 = 1 a 2 center = (h, k) radius = r radiushorizontal = a Example 1: Graph the ellipse: 25 x 2 + 16 y 2 = 400 (-4, 0) (0, 5) (0, 3) (0, 0) (4, 0) (0, -3) (0, -5) Finding Ellipse Foci: (foci-radius)2 = (major-radius)2 – (minor-radius)2 Example 2: Calculate/Find the foci above. b 2 radiusvertical = b We do not usually call ‘a’ and ‘b’ radii since it is not the same distance from the center all around the ellipse, but you may think of them as such for the purpose of locating vertices located at : (h + a, k) (h – a, k) (h, k + b) (h, k – b) Major and Minor axis is determined by knowing the longest and shortest horizontal or vertical distance across the ellipse.

Converting to Ellipse Standard Form Example: Graph the ellipse: 9 x 2 + 4 y 2 – 18 x + 16 y – 11 = 0 Move constant : X’s & Y’s together : Complete the Square: Factor 9 x 2 + 4 y 2 – 18 x +16 y = 11 (9 x 2 – 18 x ) + (4 y 2 + 16 y ) = 11 9(x 2 – 2 x ) + 4(y 2 + 4 y ) = 11 9(x 2 – 2 x + 1 ) + 4(y 2 + 4 y + 4) = 11 + 9 + 16 9(x – 1) + 4(y + 2) = 36 9 (x – 1)2 + 4(x + 2)2 = 36 Standard Form 9(x – 1)2 + 4(y + 2)2 36 (x – 1)2 4 =1 36 + (y + 2)2 9 =1 Can you graph this?

Standard Forms of Equations of Ellipses Centered at (h, k) Equation Center Major Axis Foci Vertices (h, k) Parallel to the x-axis, horizontal (h – c, k) (h + c, k) (h – a, k) (h + a, k) (h, k) Parallel to the y-axis, vertical (h, k – c) (h, k + c) (h, k – a) (h, k + a) a 2 > b 2 and b 2 = a 2 – c 2 b 2 > a 2 and a 2 = b 2 – c 2 y Major axis Focus (h + c, k) Focus (h – c, k) Major axis Vertex (h – a, k) Vertex (h + a, k) Focus (h + c, k) (h, k) Vertex (h + a, k) x Focus (h – c, k) x Vertex (h + a, k)

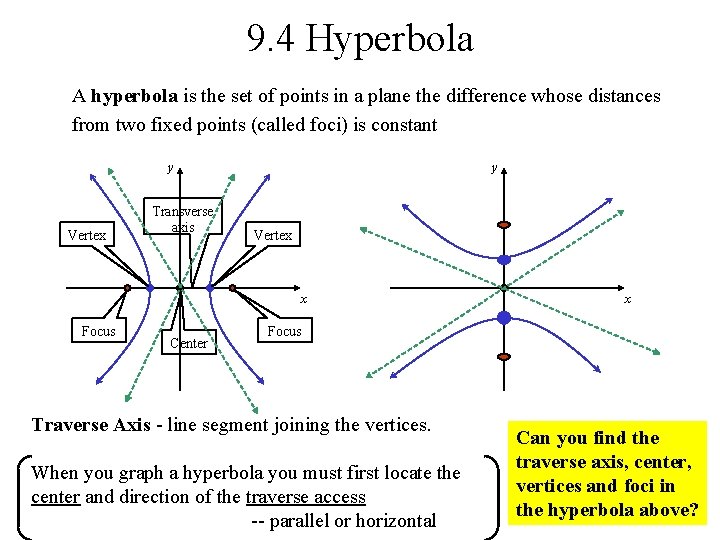
9. 4 Hyperbola A hyperbola is the set of points in a plane the difference whose distances from two fixed points (called foci) is constant y Vertex Transverse axis y Vertex x Focus Center x Focus Traverse Axis - line segment joining the vertices. When you graph a hyperbola you must first locate the center and direction of the traverse access -- parallel or horizontal Can you find the traverse axis, center, vertices and foci in the hyperbola above?

Graphing Hyperbola: (x – h)2 - (y – k)2 = 1 a 2 or (y – k)2 - (x – h)2 = 1 b 2 transverse axis: Horizontal a 2 b 2 transverse axis: Vertical center = (h, k) – BE Careful! (Foci-displacement)2 = a 2 + b 2 Verticies at center traverse-coordinate +a Asymptotes: y – k = m (x – h) center traverse-coordinate –a m = +/- y-displacement x-displacement Example 1 : Center: (3, 1) Traverse Axis: Horizontal Foci-displacement F 2 = 4 + 25 = 29 F = 29 = 5. 4 C

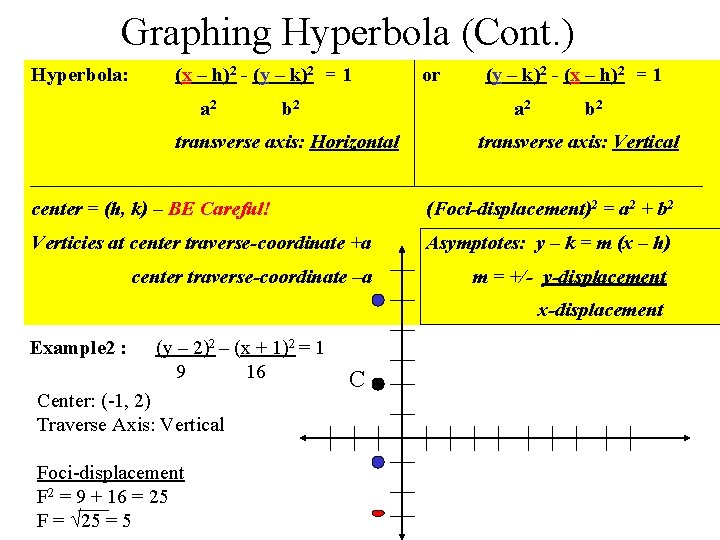
Graphing Hyperbola (Cont. ) Hyperbola: (x – h)2 - (y – k)2 = 1 a 2 b 2 or (y – k)2 - (x – h)2 = 1 a 2 transverse axis: Horizontal b 2 transverse axis: Vertical center = (h, k) – BE Careful! (Foci-displacement)2 = a 2 + b 2 Verticies at center traverse-coordinate +a Asymptotes: y – k = m (x – h) center traverse-coordinate –a m = +/- y-displacement x-displacement Example 2 : (y – 2)2 – (x + 1)2 = 1 9 16 Center: (-1, 2) Traverse Axis: Vertical Foci-displacement F 2 = 9 + 16 = 25 F = 25 = 5 C

Graphing Hyperbola (Completing the Square) Hyperbola: (x – h)2 - (y – k)2 = 1 a 2 b 2 transverse axis: Horizontal or (y – k)2 - (x – h)2 = 1 a 2 b 2 transverse axis: Vertical center = (h, k) – BE Careful! (Foci-displacement)2 = a 2 + b 2 Verticies at center traverse-coordinate +a Asymptotes: y – k = m (x – h) center traverse-coordinate –a m = +/- y-displacement x-displacement Example 3 : 4 x 2 – y 2 + 32 x + 6 y +39 = 0

Standard Forms of Equations of Hyperbolas Centered at (h, k) Equation Center Transverse Axis Foci Vertices (h, k) Parallel to the x-axis, horizontal (h – c, k) (h + c, k) (h – a, k) (h + a, k) (h, k) Parallel to the y-axis, vertical (h, k – c) (h, k + c) (h, k – a) (h, k + a) b 2 = c 2 – a 2 y Focus (h – c, k) Vertex (h + a, k) Focus (h + c, k) (h, k) Vertex (h – a, k) Vertex (h + a, k) x Focus (h – c, k) Vertex (h + a, k) x