Conic Sections 11 1 Parabola Conic Sections Parabola

Conic Sections 11. 1 Parabola

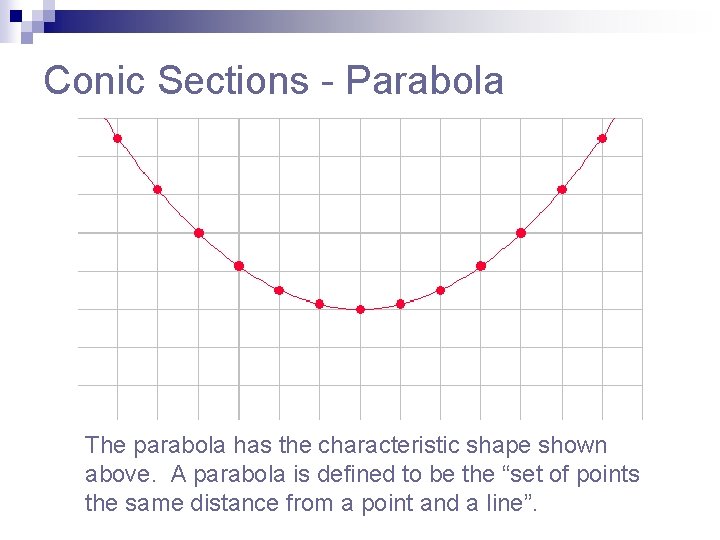
Conic Sections - Parabola The parabola has the characteristic shape shown above. A parabola is defined to be the “set of points the same distance from a point and a line”.

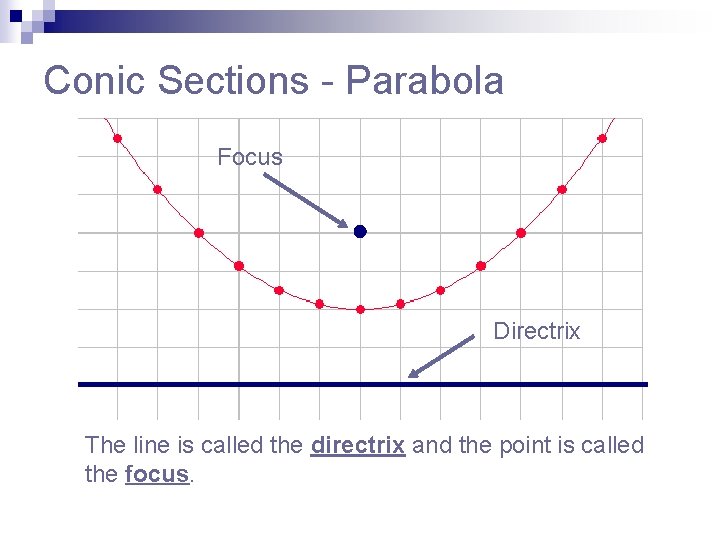
Conic Sections - Parabola Focus Directrix The line is called the directrix and the point is called the focus.

Conic Sections - Parabola Focus Vertex Axis of Symmetry Directrix The line perpendicular to the directrix passing through the focus is the axis of symmetry. The vertex is the point of intersection of the axis of symmetry with the parabola.

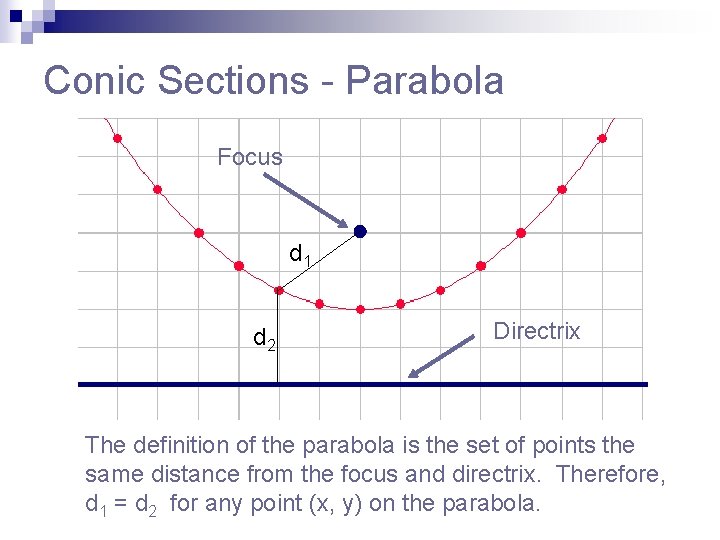
Conic Sections - Parabola Focus d 1 d 2 Directrix The definition of the parabola is the set of points the same distance from the focus and directrix. Therefore, d 1 = d 2 for any point (x, y) on the parabola.

Finding the Focus and Directrix Parabola

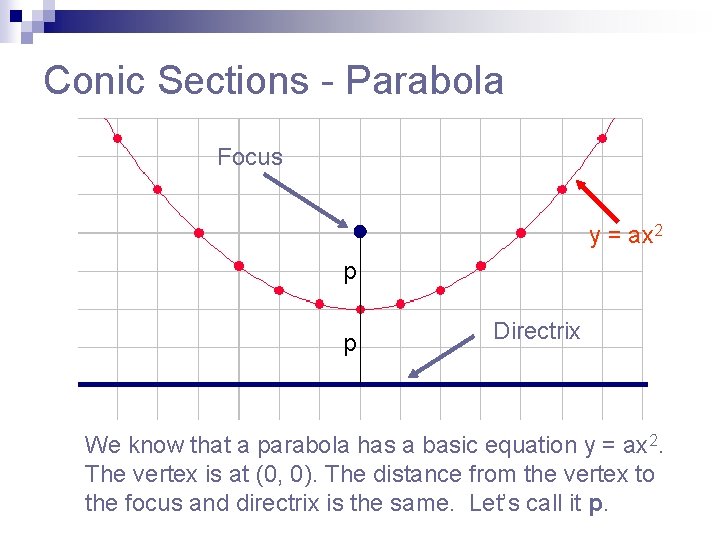
Conic Sections - Parabola Focus y = ax 2 p p Directrix We know that a parabola has a basic equation y = ax 2. The vertex is at (0, 0). The distance from the vertex to the focus and directrix is the same. Let’s call it p.

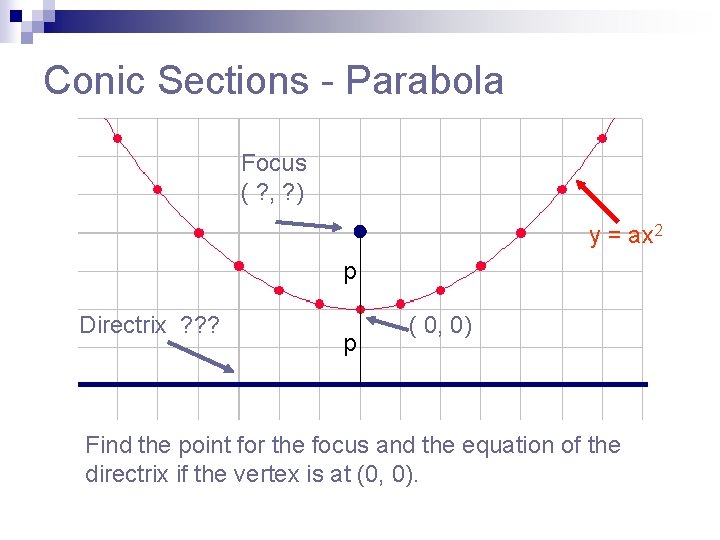
Conic Sections - Parabola Focus ( ? , ? ) y = ax 2 p Directrix ? ? ? p ( 0, 0) Find the point for the focus and the equation of the directrix if the vertex is at (0, 0).

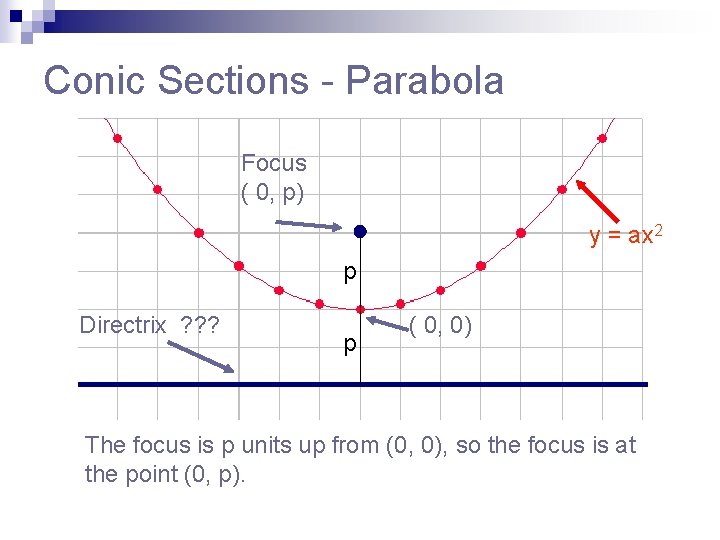
Conic Sections - Parabola Focus ( 0, p) y = ax 2 p Directrix ? ? ? p ( 0, 0) The focus is p units up from (0, 0), so the focus is at the point (0, p).

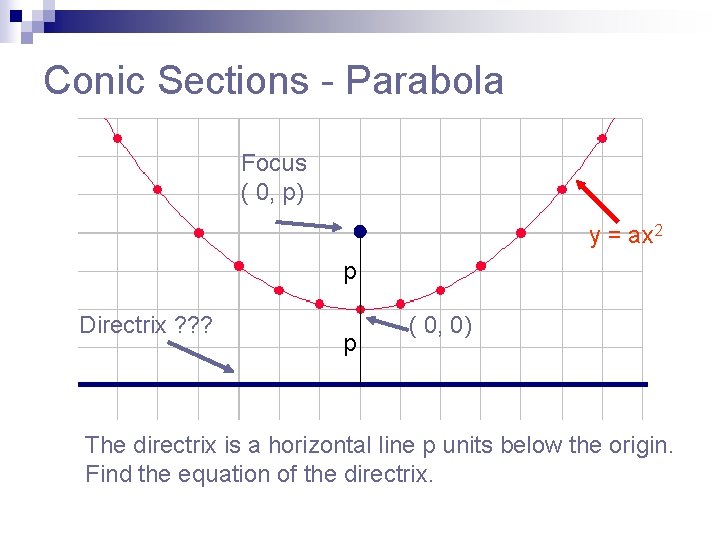
Conic Sections - Parabola Focus ( 0, p) y = ax 2 p Directrix ? ? ? p ( 0, 0) The directrix is a horizontal line p units below the origin. Find the equation of the directrix.

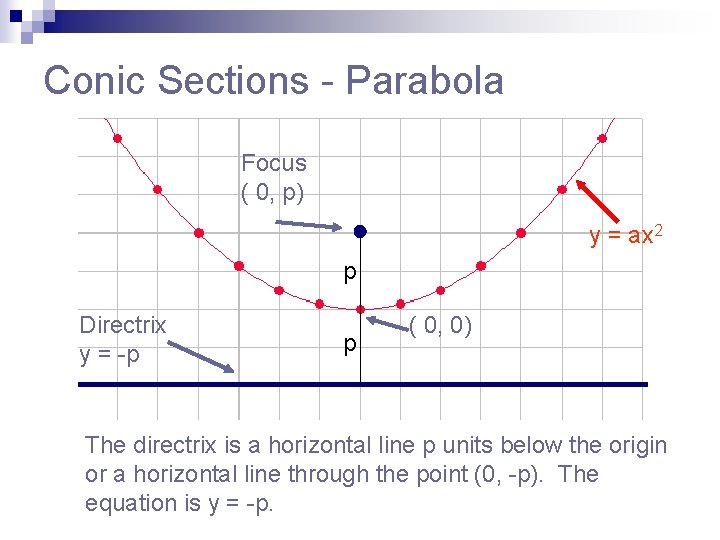
Conic Sections - Parabola Focus ( 0, p) y = ax 2 p Directrix y = -p p ( 0, 0) The directrix is a horizontal line p units below the origin or a horizontal line through the point (0, -p). The equation is y = -p.

Conic Sections - Parabola Therefore, the distance p from the vertex to the focus and the vertex to the directrix is given by the formula

Conic Sections - Parabola Using transformations, we can shift the parabola y=ax 2 horizontally and vertically. If the parabola is shifted h units right and k units up, the equation would be The vertex is shifted from (0, 0) to (h, k). Recall that when “a” is positive, the graph opens up. When “a” is negative, the graph reflects about the x-axis and opens down.

Example 1 Graph a parabola. Find the vertex, focus and directrix.

Parabola – Example 1 Make a table of values. Graph the function. Find the vertex, focus, and directrix.

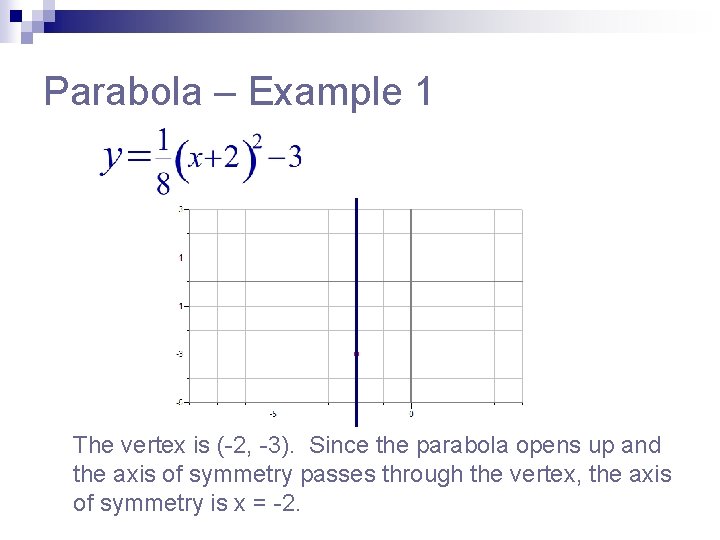
Parabola – Example 1 The vertex is (-2, -3). Since the parabola opens up and the axis of symmetry passes through the vertex, the axis of symmetry is x = -2.

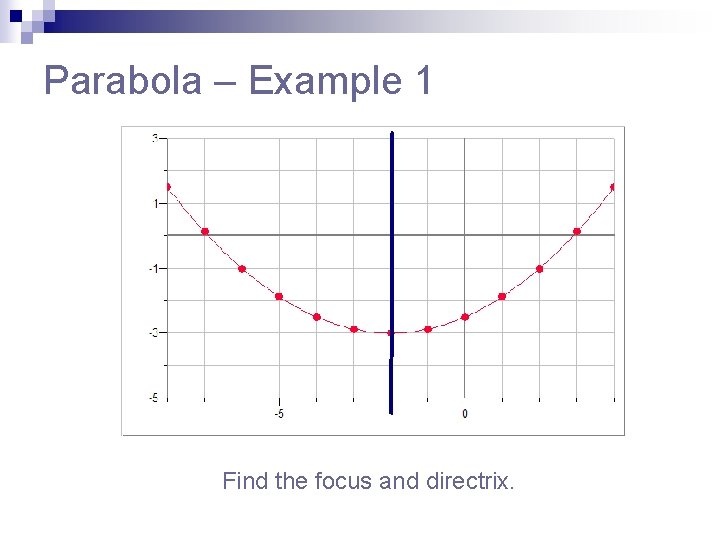
Parabola – Example 1 Find the focus and directrix.

Parabola – Example 1 The focus and directrix are “p” units from the vertex where The focus and directrix are 2 units from the vertex.

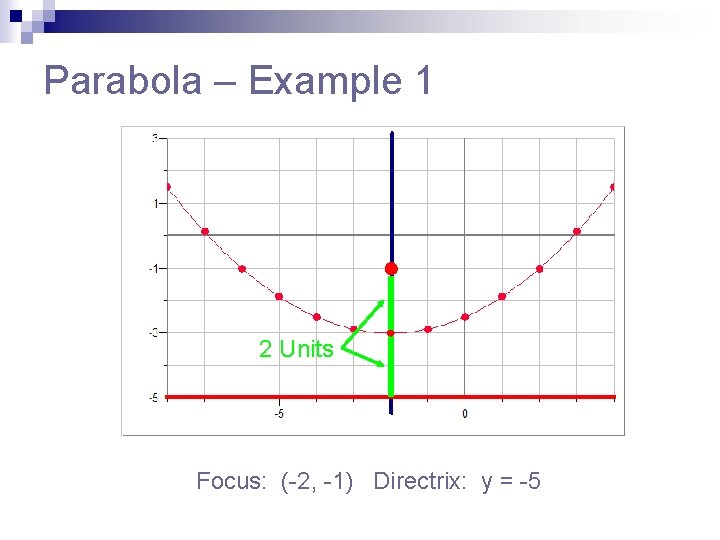
Parabola – Example 1 2 Units Focus: (-2, -1) Directrix: y = -5

Example 2 Graph a parabola using the vertex, focus, axis of symmetry and directrix.

Parabola – Example 2 Find the vertex, axis of symmetry, focus, directrix and sketch the graph.

Parabola – Example 2 The vertex is at (1, 2) with the parabola opening down. The focus is 4 units down and the directrix is 4 units up.

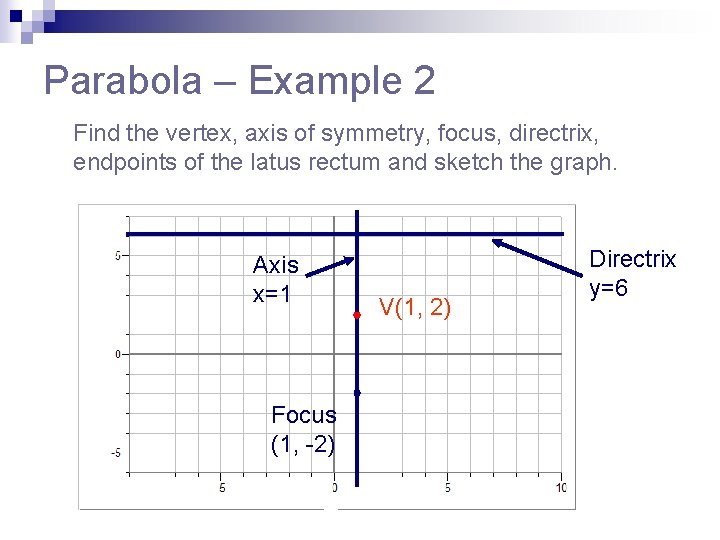
Parabola – Example 2 Find the vertex, axis of symmetry, focus, directrix, endpoints of the latus rectum and sketch the graph. Axis x=1 Focus (1, -2) V(1, 2) Directrix y=6

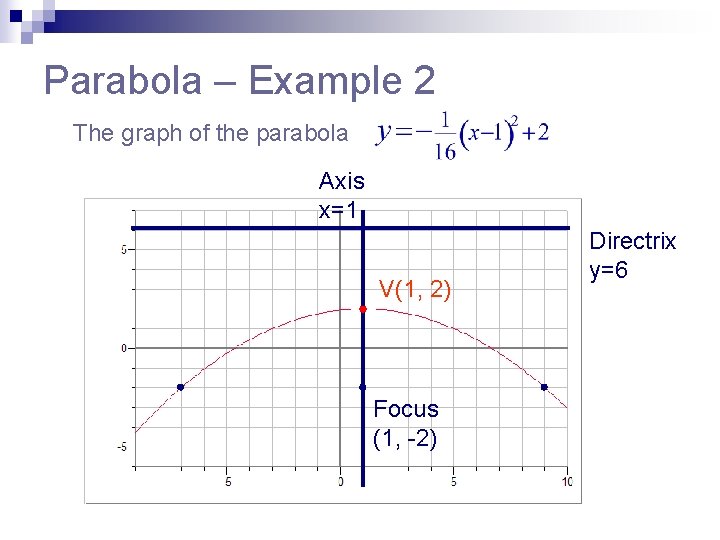
Parabola – Example 2 The graph of the parabola Axis x=1 V(1, 2) Focus (1, -2) Directrix y=6

x= 2 ay Parabola Graphing and finding the vertex, focus, directrix, & axis of symmetry.

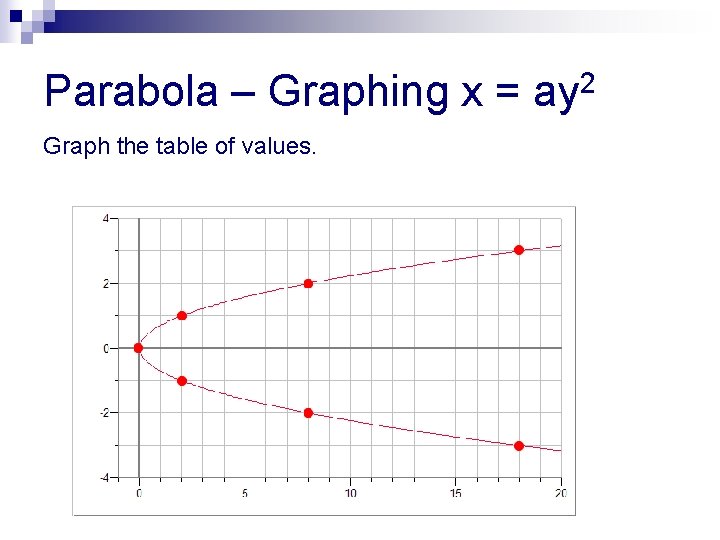
Parabola – Graphing x = ay 2 Graph the table of values.

Parabola – Graphing x = ay 2 One could follow a similar proof to show the distance from the vertex to the focus and directrix to be .

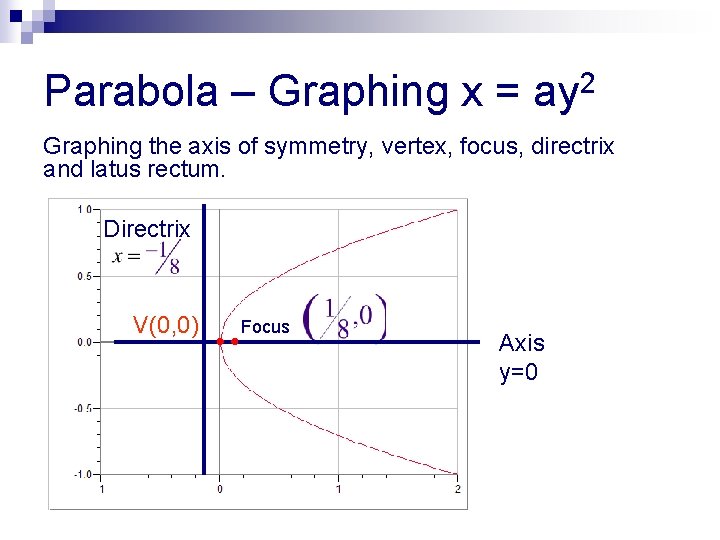
Parabola – Graphing x = ay 2 Graphing the axis of symmetry, vertex, focus, directrix and latus rectum. Directrix V(0, 0) Focus Axis y=0

x = a(y – 2 k) +h Graphing and finding the vertex, focus, directrix, & axis of symmetry.

Parabola – x = a(y – k)2 + h We have just seen that a parabola x = ay 2 opens to the right when a is positive. When a is negative, the graph will reflect about the y-axis and open to the left. When horizontal and vertical transformations are applied, a vertical shift of k units and a horizontal shift of h units will result in the equation: x = a(y – k)2 + h Note: In both cases of the parabola, the x always goes with h and the y always goes with k.

Example 3 Graphing and finding the vertex, focus, directrix, axis of symmetry and latus rectum.

Parabola – Example 3 Graph the parabola by finding the vertex, focus, directrix. What is the vertex? Remember that inside the “function” we always do the opposite. So the graph moves -1 in the y direction and -2 in the x direction. The vertex is (-2, -1) What is the direction of opening? The parabola opens to the left since it is x= and “a” is negative.

Parabola – Example 3 Graph the parabola by finding the vertex, focus, directrix. What is the distance to the focus and directrix? The distance is The parabola opens to the left with a vertex of (-2, -1) and a distance to the focus and directrix of ½. Begin the sketch of the parabola.

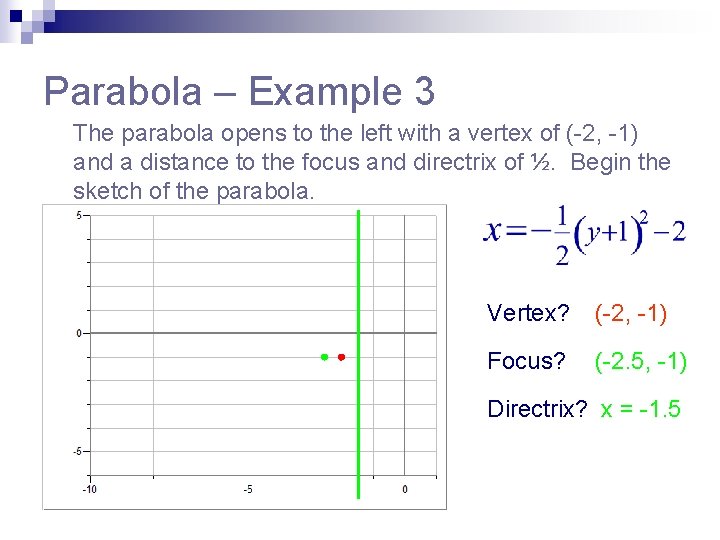
Parabola – Example 3 The parabola opens to the left with a vertex of (-2, -1) and a distance to the focus and directrix of ½. Begin the sketch of the parabola. Vertex? (-2, -1) Focus? (-2. 5, -1) Directrix? x = -1. 5

Parabola – Example 3

Parabola – Example 3 The parabola is: Vertex? (-2, -1) Focus? (-2. 5, -1) Directrix? x = -1. 5

Building a Table of Rules Parabola

Table of Rules - y = a(x - h)2 + k a>0 a<0 Opens Up Down Vertex (h, k) Focus Axis Directrix x=h x=h (h, k) x=h

Table of Rules - x = a(y - k)2 + h a>0 Opens Vertex Right a<0 Left (h, k) y=k y=k (h, k) Focus Axis Directrix (h, k) y=k

Sample Problems Parabola

Sample Problems 1. (y + 3)2 = 12(x -1) a. Find the vertex, focus, & directrix. b. Sketch the graph. c. Graph using a grapher.

Sample Problems 1. (y + 3)2 = 12(x -1) a. Find the vertex, focus, directrix, & axis of symmetry. Since the y term is squared, solve for x.

Sample Problems Find the direction of opening and vertex. The parabola opens to the right with a vertex at (1, -3). Find the distance from the vertex to the focus.

Sample Problems Find the length of the latus rectum.

Sample Problems b. Sketch the graph given: • The parabola opens to the right. • The vertex is (1, -3) • The distance to the focus and directrix is 3. • The length of the latus rectum is 12.

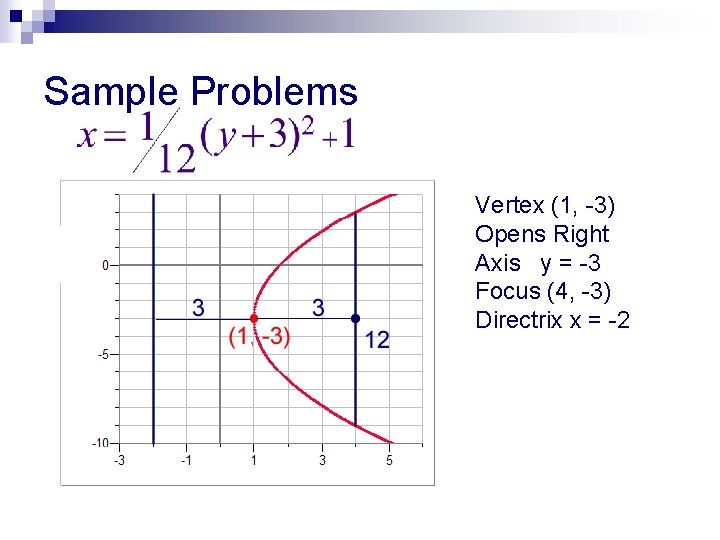
Sample Problems Vertex (1, -3) Opens Right Axis y = -3 Focus (4, -3) Directrix x = -2

Sample Problems 1. (y + 3)2 = 12(x -1) c. Graph using a grapher. Solve the equation for y. Graph as 2 separate equations in the grapher.

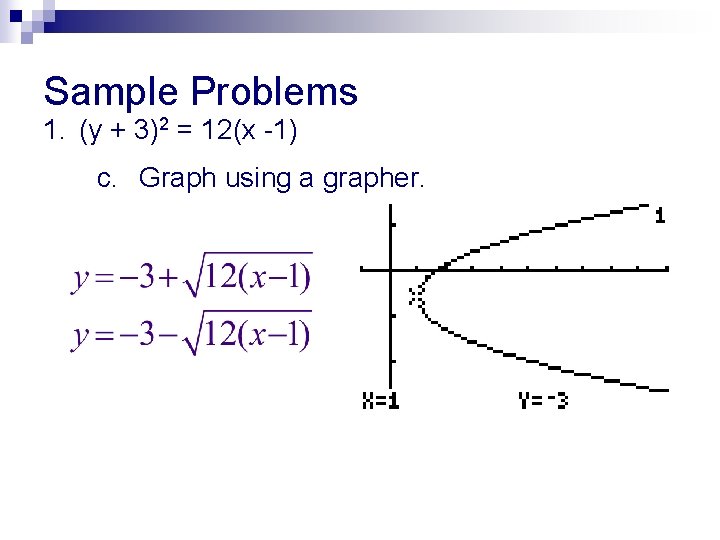
Sample Problems 1. (y + 3)2 = 12(x -1) c. Graph using a grapher.

Sample Problems 2. 2 x 2 + 8 x – 3 + y = 0 a. Find the vertex, focus, directrix, axis of symmetry. b. Sketch the graph. c. Graph using a grapher.

Sample Problems 2. 2 x 2 + 8 x – 3 + y = 0 a. Find the vertex, focus, directrix, axis of symmetry. Solve for y since x is squared. y = -2 x 2 - 8 x + 3 Complete the square. y = -2(x 2 + 4 x )+3 y = -2(x 2 + 4 x + 4 ) + 3 + 8 (-2*4) is -8. To balance the side, we must add 8. y = -2(x + 2) 2 + 11

Sample Problems 2. 2 x 2 + 8 x – 3 + y = 0 a. Find the vertex, focus, & directrix. y = -2(x + 2) 2 + 11 Find the direction of opening and the vertex. The parabola opens down with a vertex at (-2, 11). Find the distance to the focus and directrix.

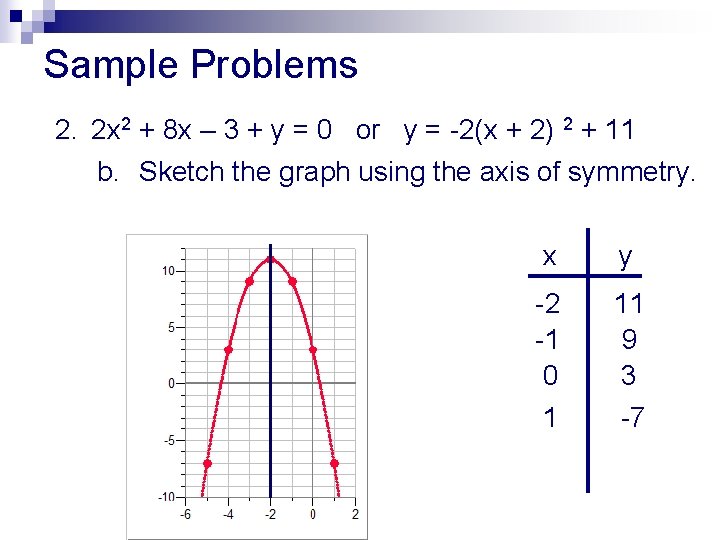
Sample Problems 2. 2 x 2 + 8 x – 3 + y = 0 or y = -2(x + 2) 2 + 11 b. Sketch the graph using the axis of symmetry. x y -2 -1 0 1 11 9 3 -7

11. 2 Ellipse

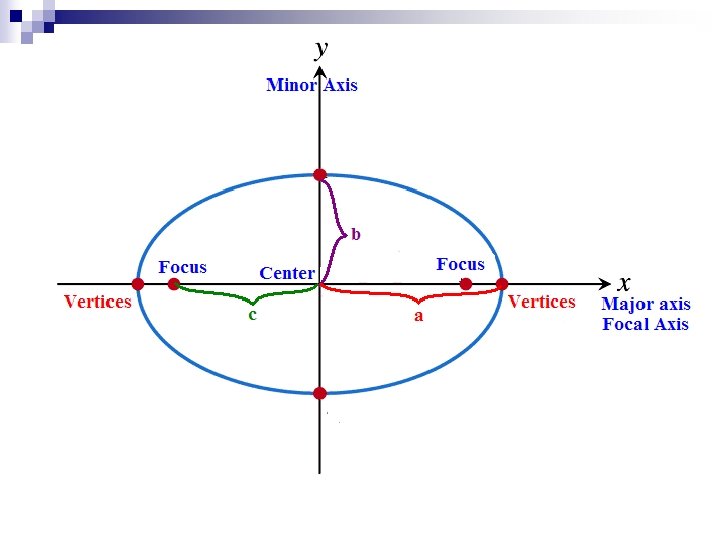
Ellipse An ellipse is the set of all points in a plane whose distance from two fixed points in the plane have a constant sum. The fixed points are the foci (plural of focus) of the ellipse.

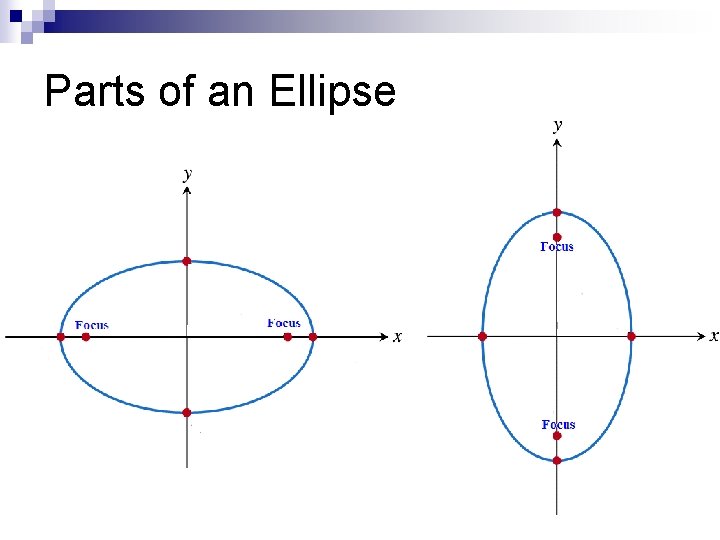
Parts of an Ellipse

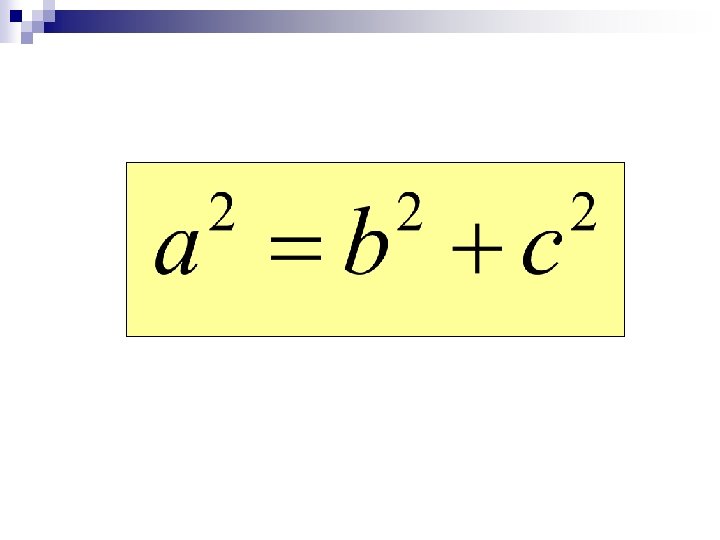
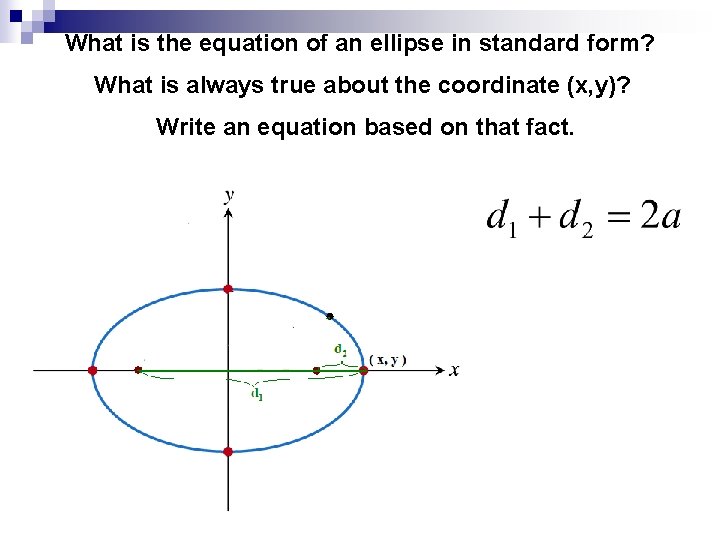
What is the equation of an ellipse in standard form? What is always true about the coordinate (x, y)? Write an equation based on that fact.

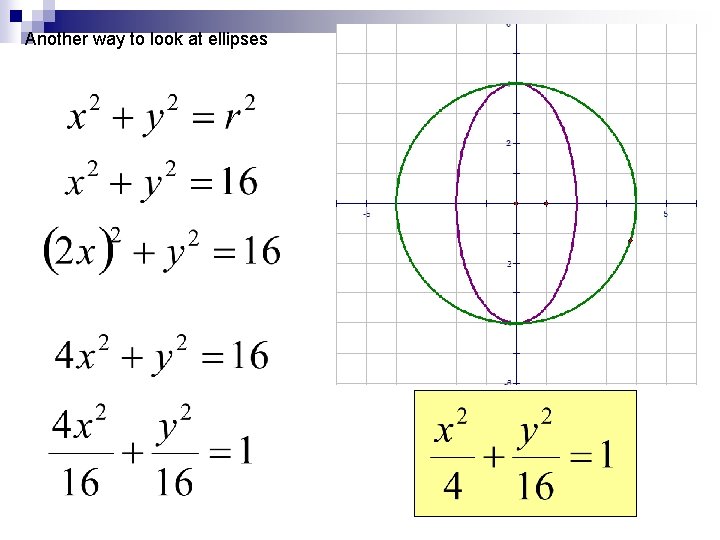
Another way to look at ellipses

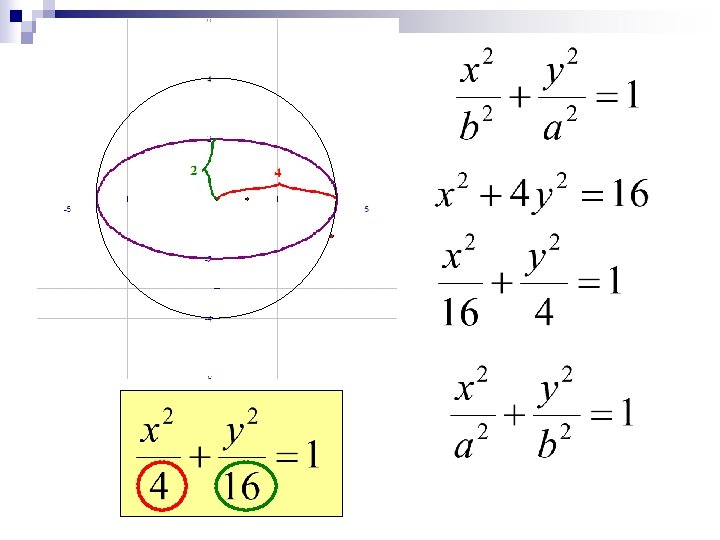
Also acceptable

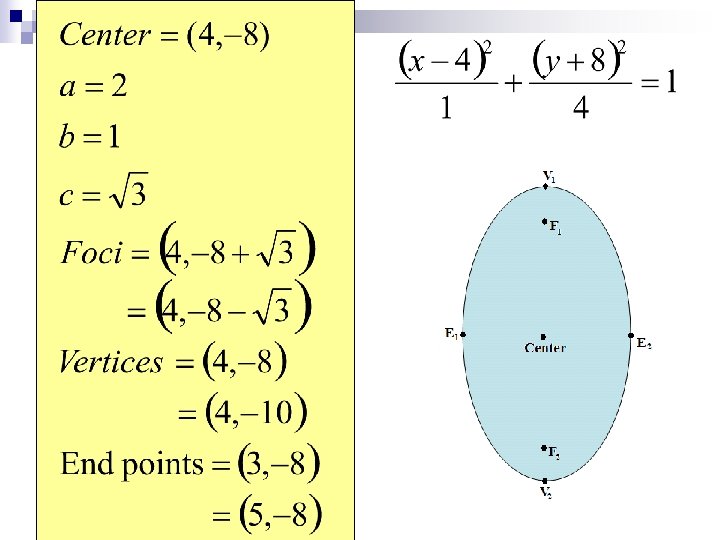
Practice 1. Center ( -1, 1) a = 3, b = 2 c = Vertices: (-1, 4) (-1, -2) Foci:

Practice 2. Find an equation of the ellipse with foci ( -4, 0) and ( 0, 0 ) and whose minor axis has a length of 2. Center ( -2, 0) c = 2, b = 1 a =

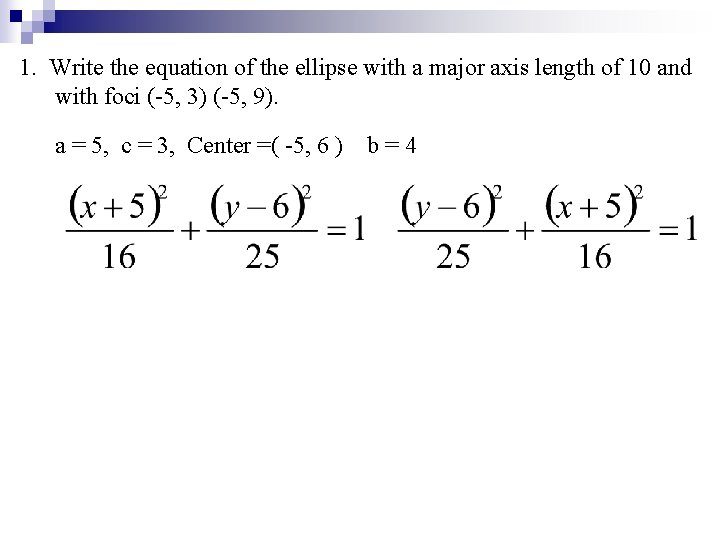
1. Write the equation of the ellipse with a major axis length of 10 and with foci (-5, 3) (-5, 9). a = 5, c = 3, Center =( -5, 6 ) b=4

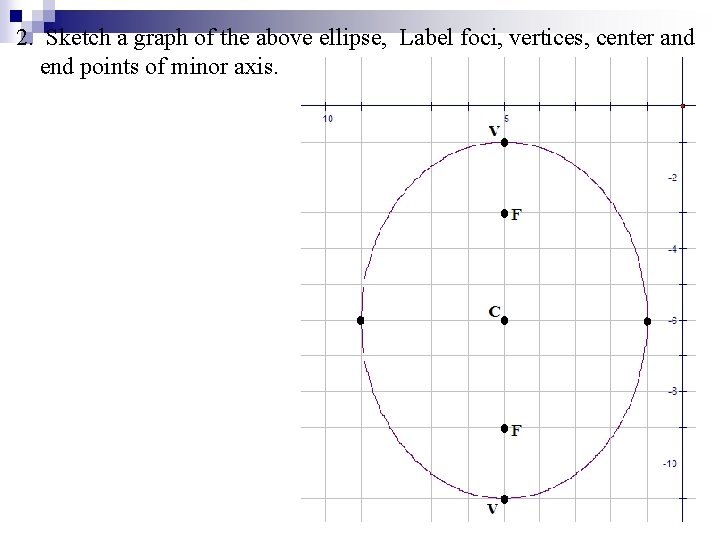
2. Sketch a graph of the above ellipse, Label foci, vertices, center and end points of minor axis.

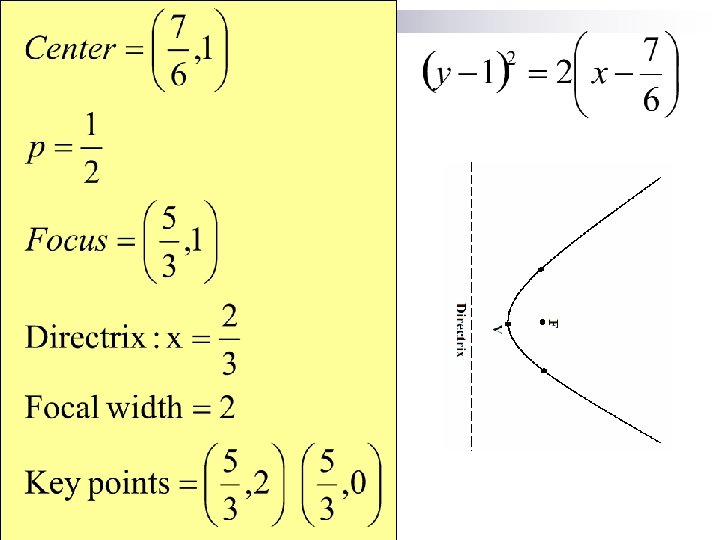
3. Write the equation of a parabola in standard form whose focus is located at the center of the above ellipse and whose directrix is y = b. (use “b” from the above ellipse). Focus = ( -5, 6) p=1 Directrix : y = 4 Vertex = (-5, 5)

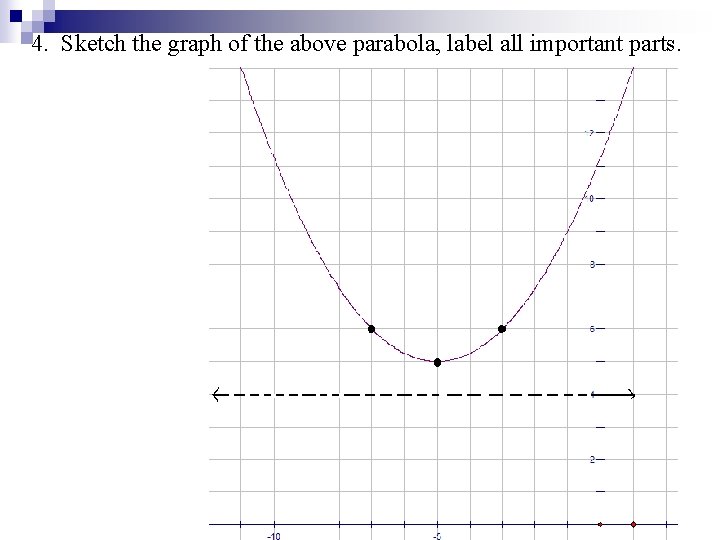
4. Sketch the graph of the above parabola, label all important parts.

a) Determine the type of conic the equation represents. b) Rewrite into standard form. c) Graph and label all major parts of the conic

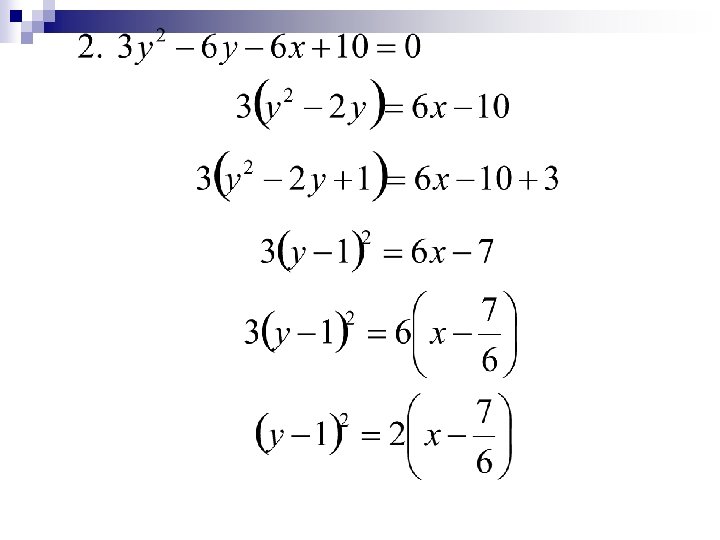
Eccentricity Circle : e = 1 Ellipse: 0 < e < 1 Hyperbola: e > 1

Section 11. 3 Hyperbolas

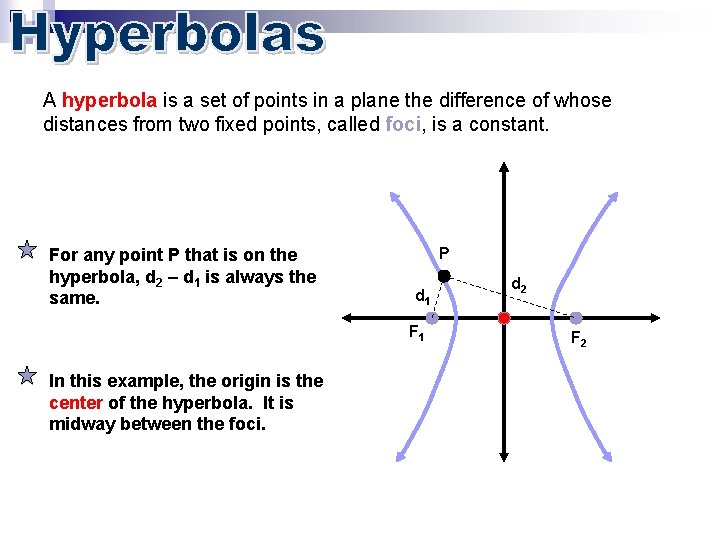
A hyperbola is a set of points in a plane the difference of whose distances from two fixed points, called foci, is a constant. For any point P that is on the hyperbola, d 2 – d 1 is always the same. P d 1 F 1 In this example, the origin is the center of the hyperbola. It is midway between the foci. d 2 F 2

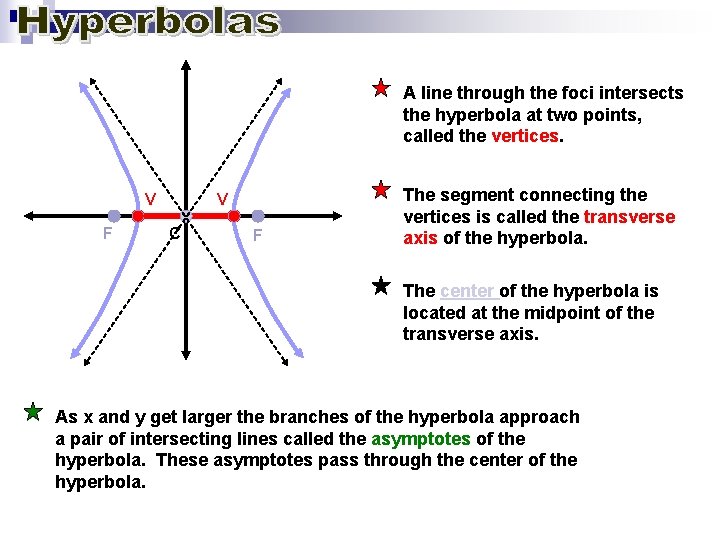
A line through the foci intersects the hyperbola at two points, called the vertices. V F V C F The segment connecting the vertices is called the transverse axis of the hyperbola. The center of the hyperbola is located at the midpoint of the transverse axis. As x and y get larger the branches of the hyperbola approach a pair of intersecting lines called the asymptotes of the hyperbola. These asymptotes pass through the center of the hyperbola.

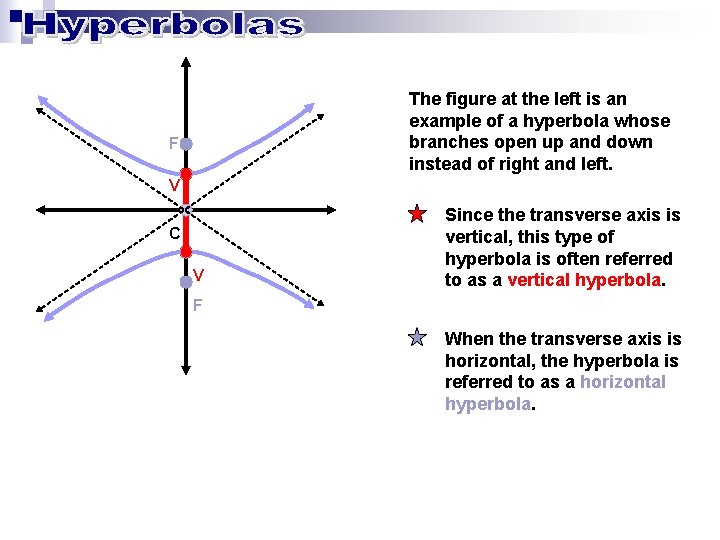
The figure at the left is an example of a hyperbola whose branches open up and down instead of right and left. F V C V Since the transverse axis is vertical, this type of hyperbola is often referred to as a vertical hyperbola. F When the transverse axis is horizontal, the hyperbola is referred to as a horizontal hyperbola.

(x – h)2 – (y – k)2 = 1 a 2 b 2 (y – k)2 – (x – h)2 = 1 a 2 b 2 Horizontal Hyperbola Vertical Hyperbola The center of a hyperbola is at the point (h, k) in either form For either hyperbola, c 2 = a 2 + b 2 Where c is the distance from the center to a focus point. The equations of the asymptotes are y=± x and y= ± x

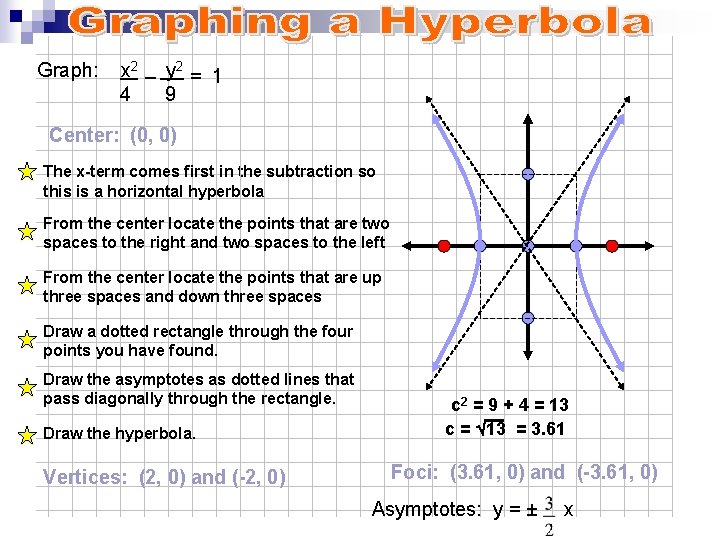
Graph: x 2 – y 2 = 1 4 9 Center: (0, 0) The x-term comes first in the subtraction so this is a horizontal hyperbola From the center locate the points that are two spaces to the right and two spaces to the left From the center locate the points that are up three spaces and down three spaces Draw a dotted rectangle through the four points you have found. Draw the asymptotes as dotted lines that pass diagonally through the rectangle. Draw the hyperbola. Vertices: (2, 0) and (-2, 0) c 2 = 9 + 4 = 13 c = Ö 13 = 3. 61 Foci: (3. 61, 0) and (-3. 61, 0) Asymptotes: y = ± x

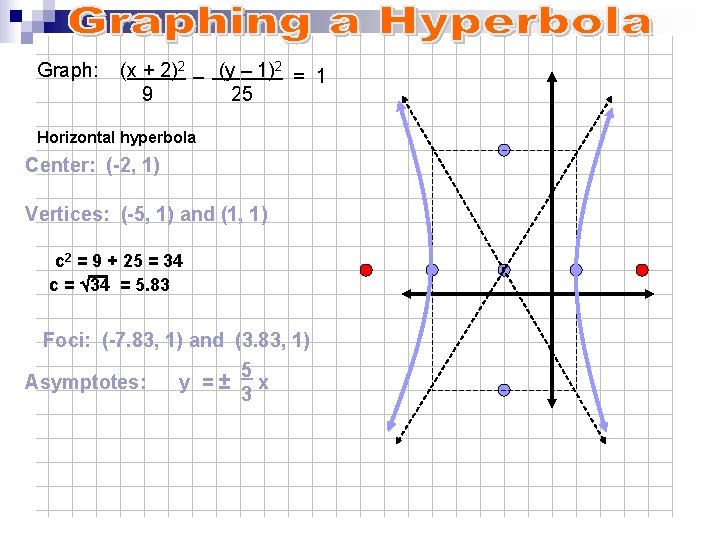
Graph: (x + 2)2 – (y – 1)2 = 1 9 25 Horizontal hyperbola Center: (-2, 1) Vertices: (-5, 1) and (1, 1) c 2 = 9 + 25 = 34 c = Ö 34 = 5. 83 Foci: (-7. 83, 1) and (3. 83, 1) 5 Asymptotes: y =± x 3

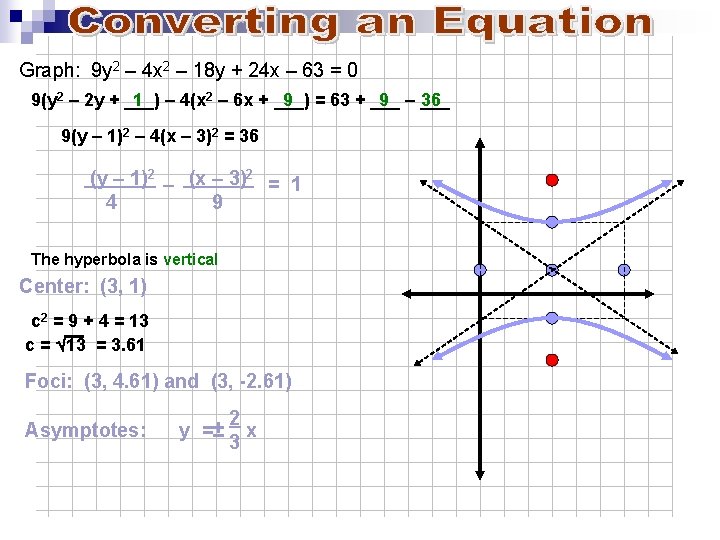
Graph: 9 y 2 – 4 x 2 – 18 y + 24 x – 63 = 0 9(y 2 – 2 y + ___) 1 – 4(x 2 – 6 x + ___) 9 = 63 + ___ 9 – ___ 36 9(y – 1)2 – 4(x – 3)2 = 36 (y – 1)2 – (x – 3)2 = 1 4 9 The hyperbola is vertical Center: (3, 1) c 2 = 9 + 4 = 13 c = Ö 13 = 3. 61 Foci: (3, 4. 61) and (3, -2. 61) Asymptotes: y =± 2 x 3

Find the standard form of the equation of a hyperbola given: Foci: (-7, 0) and (7, 0) Vertices: (-5, 0) and (5, 0) 8 Horizontal hyperbola Center: (0, 0) a 2 = 25 and c 2 = 49 F V C V F c 2 = a 2 + b 2 49 = 25 + b 2 = 24 (x – h)2 – (y – k)2 = 1 a 2 b 2 x 2 y 2 – 25 24 = 1 10

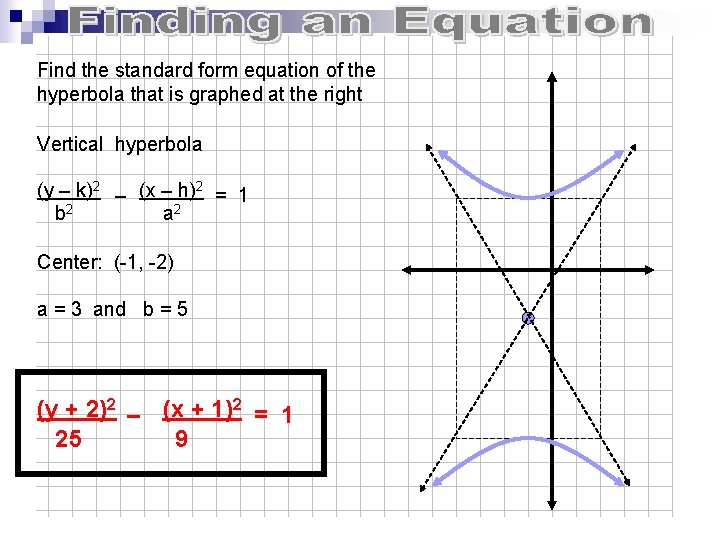
Find the standard form equation of the hyperbola that is graphed at the right Vertical hyperbola (y – k)2 – (x – h)2 = 1 b 2 a 2 Center: (-1, -2) a = 3 and b = 5 (y + 2)2 – (x + 1)2 = 1 25 9

Using Polar Coordinates Graphing and converting polar and rectangular coordinates

Graphing Polar Coordinates A The grid at the left is a polar grid. The typical angles of 30 o, 45 o, 90 o, … are shown on the graph along with circles of radius 1, 2, 3, 4, and 5 units. Points in polar form are given as (r, ß ) where r is the radius to the point and ß is the angle of the point. On one of your polar graphs, plot the point (3, 90 o)? The point on the graph labeled A is correct.

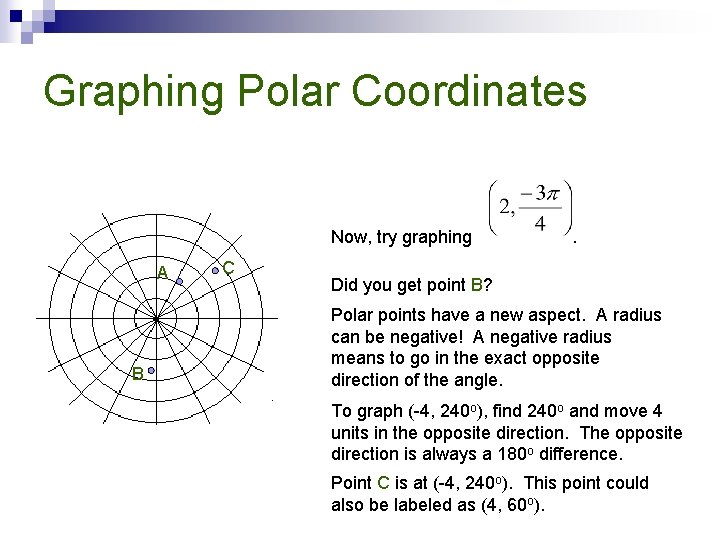
Graphing Polar Coordinates Now, try graphing A B C . Did you get point B? Polar points have a new aspect. A radius can be negative! A negative radius means to go in the exact opposite direction of the angle. To graph (-4, 240 o), find 240 o and move 4 units in the opposite direction. The opposite direction is always a 180 o difference. Point C is at (-4, 240 o). This point could also be labeled as (4, 60 o).

Graphing Polar Coordinates A B C How would you write point A with a negative radius? A correct answer would be (-3, 270 o) or (-3, -90 o). In fact, there an infinite number of ways to label a single polar point. Is (3, 450 o) the same point? Don’t forget, you can also use radian angles as well as angles in degrees. On your own, find at least 4 different polar coordinates for point B.

Graphing Polar Coordinates A B C On your own, find at least 4 different polar coordinates for point B. There are many possible answers. Here are just a few. (2, 225 o), (2, -135 o) (-2, 45 o), (-2, -315 o) One could add or subtract 360 o to any of the above angles. Radians would result in: (2, 5π/4), (2, -3π/4) (-2, π/4), (-2, -7π/4) One could add or subtract 2π to any previous radian angle.

Converting from Rectangular to Polar Find the polar form for the rectangular point (4, 3) r ß 4 3 To find the polar coordinate, we must calculate the radius and angle to the given point. We can use our knowledge of right triangle trigonometry to find the radius and angle. r 2 = 3 2 + 4 2 r 2 = 25 r=5 tan ß = ¾ ß = tan-1(¾) ß = 36. 87 o or 0. 64 rad The polar form of the rectangular point (4, 3) is (5, 36. 87 o)

Converting from Rectangular to Polar In general, the rectangular point (x, y) is converted to polar form (r, θ) by: 1. Finding the radius (x, y) r ß x y r 2 = x 2 + y 2 2. Finding the angle tan ß = y/x or ß = tan-1(y/x) Recall that some angles require the angle to be converted to the appropriate quadrant. Note: This is just like finding the length and direction angle of a vector!

Converting from Rectangular to Polar On your own, find polar form for the point (-2, 3) r 2 = (-2)2 + 32 r 2 = 4 + 9 r 2 = 13 r= However, the angle must be in the second quadrant, so we add 180 o to the answer and get an angle of 123. 70 o. The polar form is ( , 123. 70 o)

Converting from Polar to Rectanglar Convert the polar point (4, 30 o) to rectangular coordinates. We are given the radius of 4 and angle of 30 o. Find the values of x and y. 4 30 o y Using trig to find the values of x and y, we know that cos ß = x/r or x = r cos ß. Also, sin ß = y/r or y = r sin ß. x The point in rectangular form is:

Converting from Polar to Rectanglar On your own, convert (3, 5π/3) to rectangular coordinates. We are given the radius of 3 and angle of 5π/3 or 300 o. Find the values of x and y. -60 o The point in rectangular form is:

Rectangular and Polar Equations in rectangular form use variables (x, y), while equations in polar form use variables (r, ß) where ß is an angle. Converting from one form to another involves changing the variables from one form to the other. We have already used all of the conversions which are necessary. Converting Polar to Rectangular cos ß = x/r sin ß = y/r tan ß = y/x r 2 = x 2 + y 2 Converting Rectanglar to Polar x = r cos ß y = r sin ß x 2 + y 2 = r 2

Convert Rectangular Equations to Polar Equations The goal is to change all x’s and y’s to r’s and ß’s. When possible, solve for r. Example 1: Convert x 2 + y 2 = 16 to polar form. Since x 2 + y 2 = r 2, substitute into the equation. r 2 = 16 Simplify. r=4 r = 4 is the equivalent polar equation to x 2 + y 2 = 16

Convert Rectangular Equations to Polar Equations Example 2: Convert y = 3 to polar form. Since y = r sin ß, substitute into the equation. r sin ß = 3 Solve for r when possible. r = 3 / sin ß r = 3 csc ß is the equivalent polar equation.

Convert Rectangular Equations to Polar Equations Example 3: Convert (x - 3)2 + (y + 3)2 = 18 to polar form. Square each binomial. x 2 – 6 x + 9 + y 2 + 6 y + 9 = 18 Since x 2 + y 2 = r 2, re-write and simplify by combining like terms. x 2 + y 2 – 6 x + 6 y = 0 Substitute r 2 for x 2 + y 2, r cos ß for x and r sin ß for y. r 2 – 6 rcos ß + 6 rsin ß = 0 Factor r as a common factor. r(r – 6 cos ß + 6 sin ß) = 0 r = 0 or r – 6 cos ß + 6 sin ß = 0 Solve for r: r = 0 or r = 6 cos ß – 6 sin ß

Convert Polar Equations to Rectangular Equations The goal is to change all r’s and ß’s to x’s and y’s. Example 1: Convert r = 4 to rectangular form. Since r 2 = x 2 + y 2, square both sides to get r 2 = 16 Substitute. x 2 + y 2 = 16 is the equivalent polar equation to r = 4

Convert Polar Equations to Rectangular Equations Example 2: Convert r = 5 cos ß to rectangular form. Since cos ß = x/r, substitute for cos ß. Multiply both sides by r. r 2 = 5 x Substitute for r 2. x 2 + y 2 = 5 x is rectangular form.

Convert Polar Equations to Rectangular Equations Example 3: Convert r = 2 csc ß to rectangular form. Since csc ß = r/y, substitute for csc ß. Multiply both sides by y/r. Simplify y = 3 is rectangular form.