Lesson 1 2 Segments and Rays Lesson 1










- Slides: 14

Lesson 1 -2 Segments and Rays Lesson 1 -2: Segments and Rays 1

Postulates Definition: An assumption that needs no explanation. Examples: • Through any two points there is exactly one line. • A line contains at least two points. • Through any three points, there is exactly one plane. • A plane contains at least three points. Lesson 1 -2: Segments and Rays 2

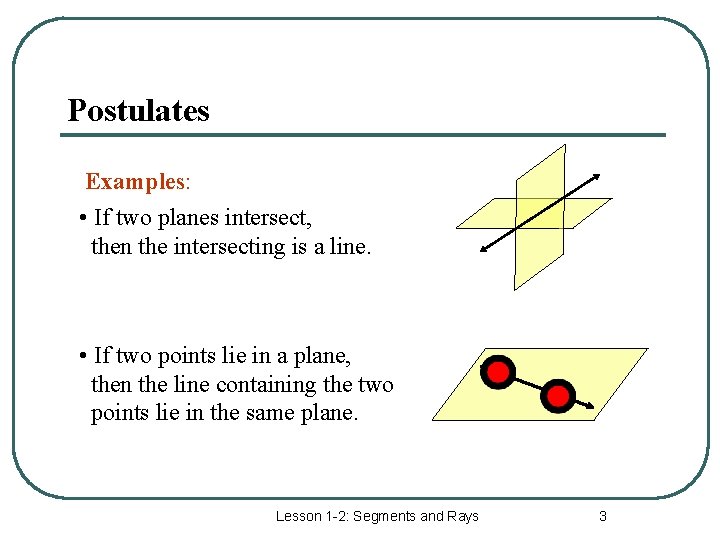
Postulates Examples: • If two planes intersect, then the intersecting is a line. • If two points lie in a plane, then the line containing the two points lie in the same plane. Lesson 1 -2: Segments and Rays 3

The Ruler Postulate: Points on a line can be paired with the real numbers in such a way that: • Any two chosen points can be paired with 0 and 1. • The distance between any two points on a number line is the absolute value of the difference of the real numbers corresponding to the points. Formula: Take the absolute value of the difference of the two coordinates a and b: │a – b │ Lesson 1 -2: Segments and Rays 4

Ruler Postulate : Example Find the distance between P and K. Note: The coordinates are the numbers on the ruler or number line! The capital letters are the names of the points. Therefore, the coordinates of points P and K are 3 and -2 respectively. Substituting the coordinates in the formula │a – b │ PK = | 3 - -2 | = 5 Remember : Distance is always positive Lesson 1 -2: Segments and Rays 5

Between Definition: X is between A and B if AX + XB = AB AX + XB > AB Lesson 1 -2: Segments and Rays 6

Segment Definition: Part of a line that consists of two points called the endpoints and all points between them. How to sketch: How to name: AB (without a symbol) means the length of the segment or the distance between points A and B. Lesson 1 -2: Segments and Rays 7

The Segment Addition Postulate: If C is between A and B, then AC + CB = AB. Example: If AC = x , CB = 2 x and AB = 12, then, find x, AC and CB. 2 x x Step 1: Draw a figure 12 Step 2: Label fig. with given info. AC + CB = AB x + 2 x = 12 Step 3: Write an equation Step 4: Solve and find all the answers 3 x = 12 x = 4 Lesson 1 -2: Segments and Rays x = 4 AC = 4 CB = 8 8

Congruent Segments Definition: Segments with equal lengths. (congruent symbol: Congruent segments can be marked with dashes. If numbers are equal the objects are congruent. AB: the segment AB ( an object ) AB: the distance from A to B ( a number ) Correct notation: Incorrect notation: Lesson 1 -2: Segments and Rays 9 )

Midpoint Definition: A point that divides a segment into two congruent segments Formulas: On a number line, the coordinate of the midpoint of a segment whose endpoints have coordinates a and b is. In a coordinate plane, the coordinates of the midpoint of a segment whose endpoints have coordinates and is . Lesson 1 -2: Segments and Rays 10

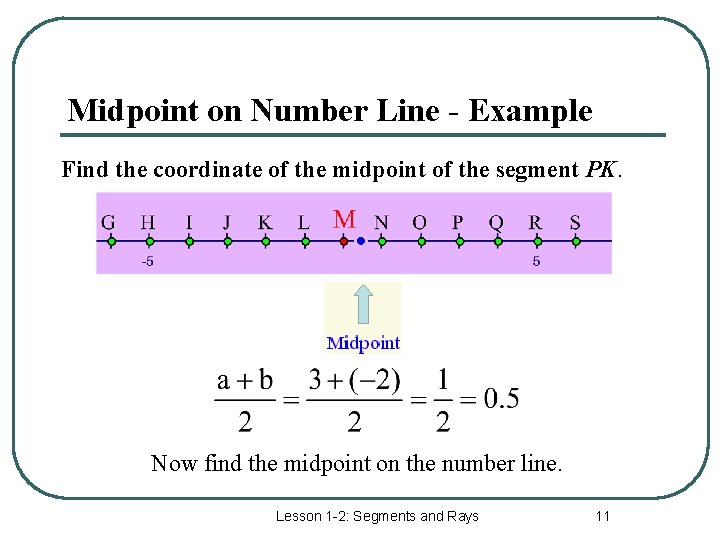
Midpoint on Number Line - Example Find the coordinate of the midpoint of the segment PK. Now find the midpoint on the number line. Lesson 1 -2: Segments and Rays 11

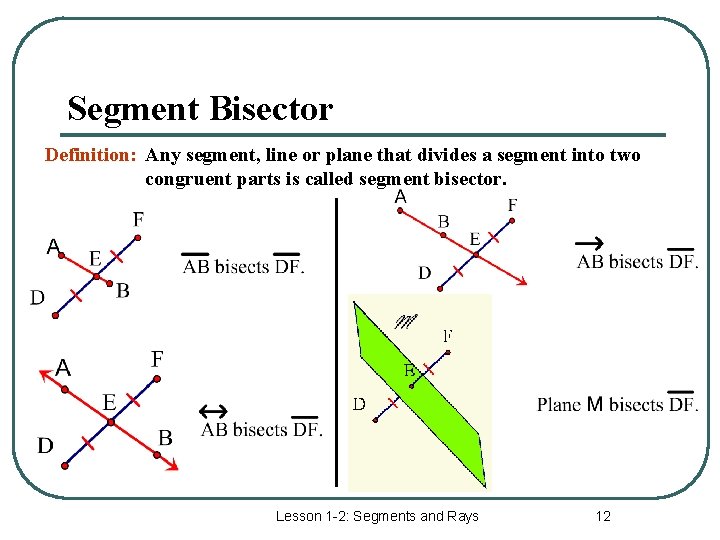
Segment Bisector Definition: Any segment, line or plane that divides a segment into two congruent parts is called segment bisector. Lesson 1 -2: Segments and Rays 12

Ray Definition: RA and all points Y such that A is between R and Y. How to sketch: How to name: ( the symbol RA is read as “ray RA” ) Lesson 1 -2: Segments and Rays 13

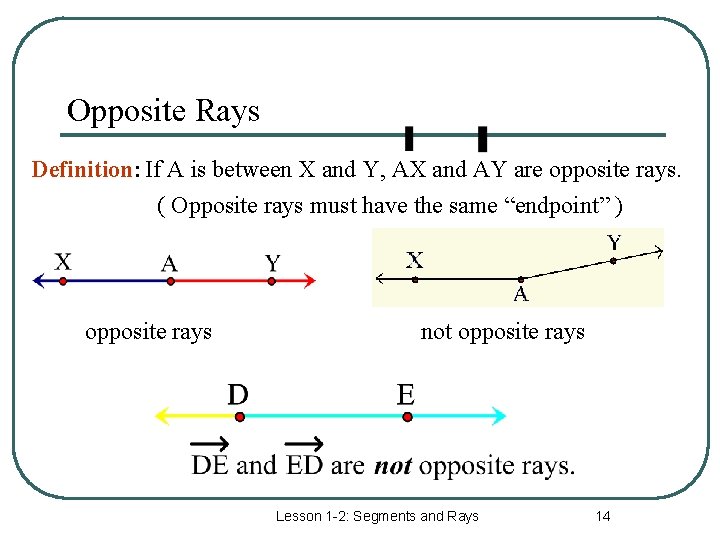
Opposite Rays Definition: If A is between X and Y, AX and AY are opposite rays. ( Opposite rays must have the same “endpoint” ) opposite rays not opposite rays Lesson 1 -2: Segments and Rays 14