Lesson 1 5 Division of Segments and Angles







- Slides: 12

Lesson 1. 5 Division of Segments and Angles Objective: Identify midpoints and bisectors of segments, trisection points and trisectors of segments, angle bisectors and trisectors.

Definitions Def. A point (or segment, ray, or line) that divides a segment into two congruent segments bisects the segment. The bisection point is called the midpoint of the segment. Y A Note: Only segments have midpoints! M B X Why can’t a ray or line have a midpoint? X X is not a midpoint Y Y is not a midpoint

Example If D is the midpoint of segment FE, what conclusions can we draw? G F Conclusions: D E

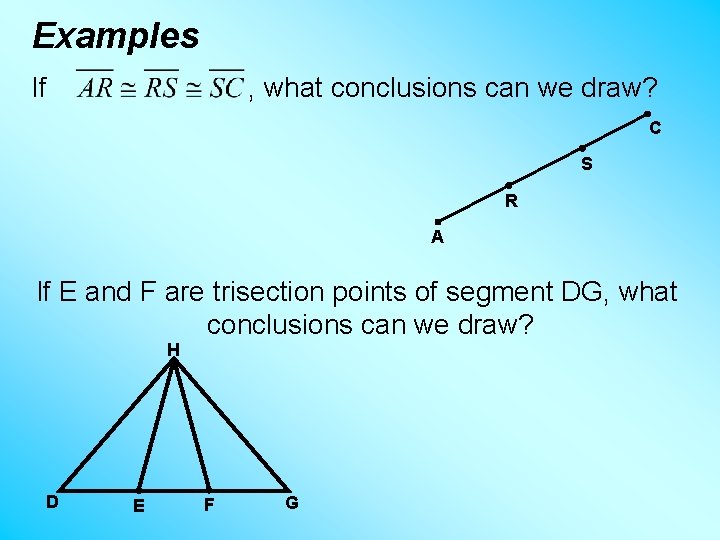
Definitions A segment divided into three congruent parts is said to be trisected. Def. Two points (or segments, rays, or lines) that divides a segment into 3 congruent segments trisect the segment. The 2 points at which the segment is divided are called trisections points. Note: One again, only segments have trisection points!

Examples If , what conclusions can we draw? C S R A If E and F are trisection points of segment DG, what conclusions can we draw? H D E F G

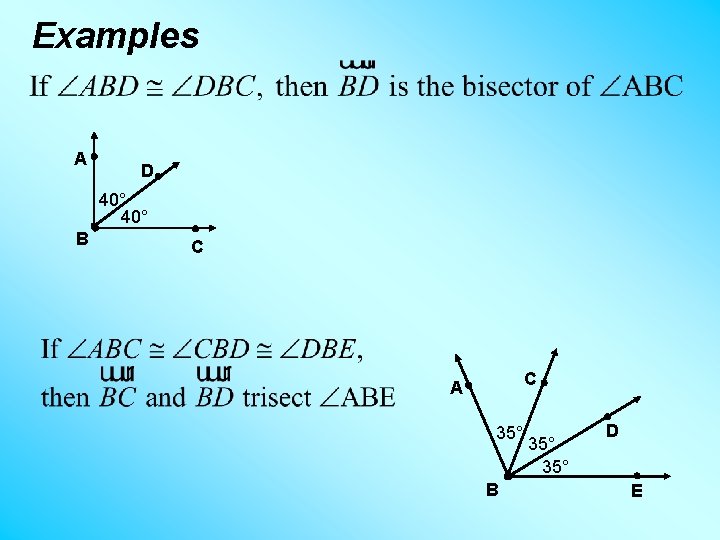
Definitions Like a segment, angles can also be bisected and trisected. Def. A ray that divides an angle into 2 congruent angles bisects the angle. The dividing ray is called the angle bisector. Def. Two rays that divide an angle into 3 congruent angles trisects the angle. The 2 dividing rays are called angle trisectors.

Examples A D 40° B C C A 35° B 35° D E

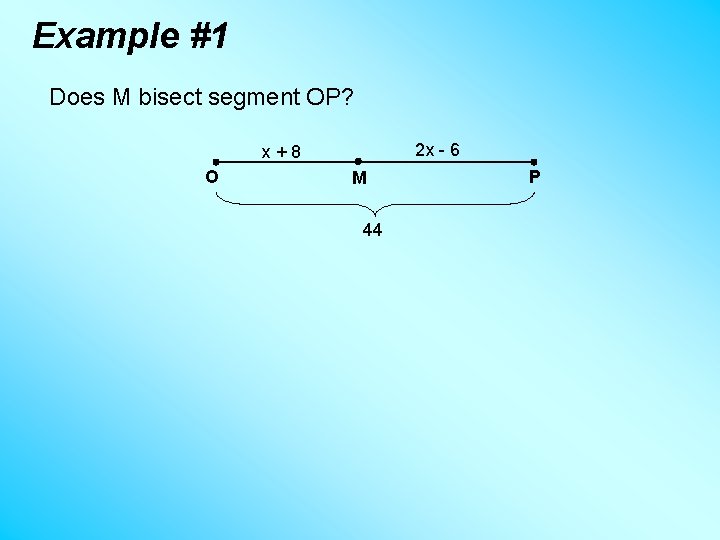
Example #1 Does M bisect segment OP? 2 x - 6 x+8 O M 44 P

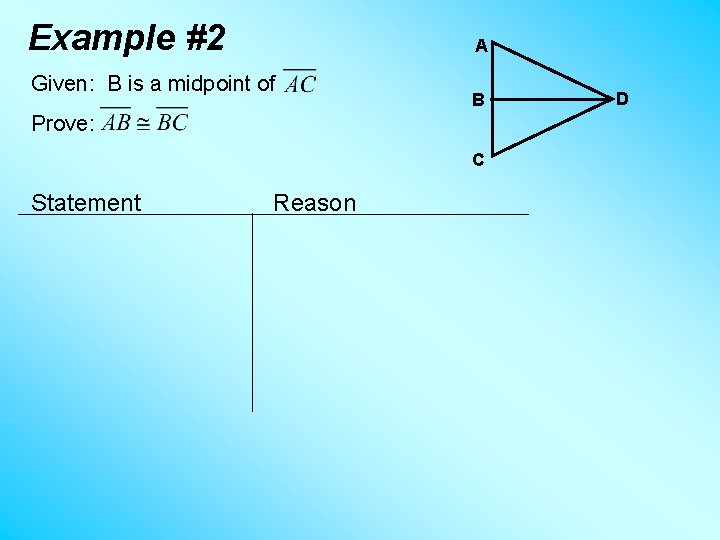
Example #2 A Given: B is a midpoint of B Prove: C Statement Reason D

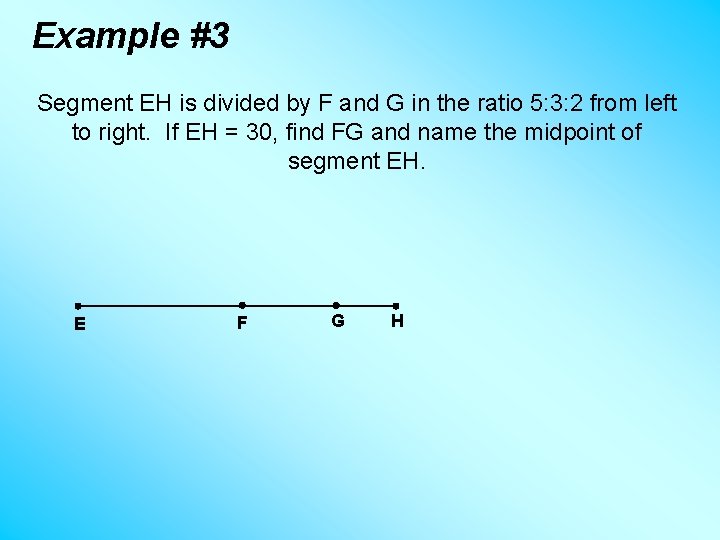
Example #3 Segment EH is divided by F and G in the ratio 5: 3: 2 from left to right. If EH = 30, find FG and name the midpoint of segment EH. E F G H

Classwork 1. 1 -1. 3 Review Worksheet

Homework Lesson 1. 5 Worksheet