Measuring angles and Segments End of Lecture Start

Measuring angles and Segments End of Lecture / Start of Lecture mark CH 1 -3 Geometry

Measuring angles and Segments Warm Up Simplify. 1. 7 – (– 3) 10 2. – 1 – (– 13) 12 3. |– 7 – 1| 8 Solve each equation. 4. 2 x + 3 = 9 x – 11 x=2 5. 3 x = 4 x – 5 x=5 6. How many numbers are there between and ? Infinitely many CH 1 -3 Geometry

Measuring angles and Segments Vocabulary coordinate midpoint distance bisect length segment bisector construction between congruent segments CH 1 -3 Geometry

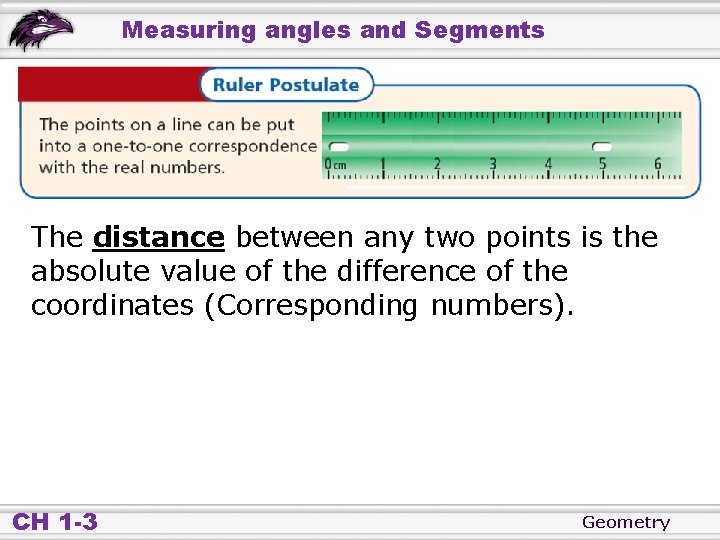
Measuring angles and Segments A ruler can be used to measure the distance between two points. A point corresponds to one and only one number on a ruler. The number is called a coordinate. CH 1 -3 Geometry

Measuring angles and Segments Postulate • Postulate is an accepted statement of facts. CH 1 -3 Geometry

Measuring angles and Segments The distance between any two points is the absolute value of the difference of the coordinates (Corresponding numbers). CH 1 -3 Geometry

Measuring angles and Segments If the coordinates of points A and B are a and b, then the distance between A and B is |a – b| or |b – a|. The distance between A and B is also called the length of AB, or AB. CH 1 -3 A B a b AB = |a – b| or |b - a| Geometry

Measuring angles and Segments Example 1: Finding the Length of a Segment Find each length. A. BC BC = |1 – 3| =2 CH 1 -3 B. AC AC = |– 2 – 3| = |– 5| =5 Geometry

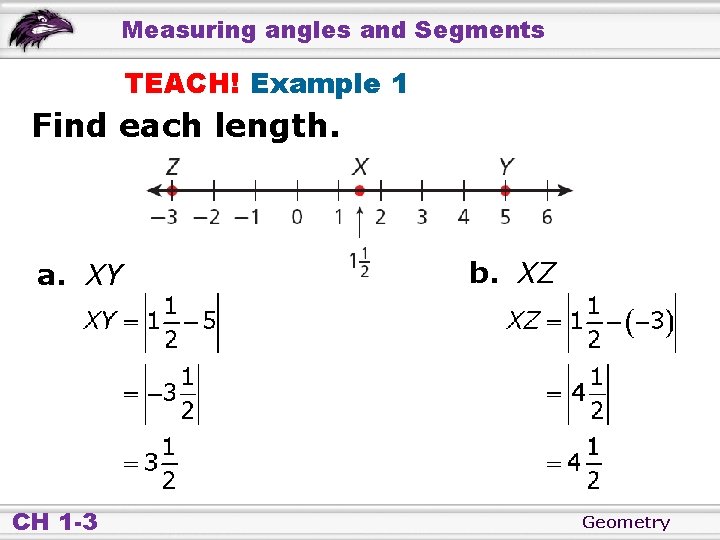
Measuring angles and Segments TEACH! Example 1 Find each length. a. XY CH 1 -3 b. XZ Geometry

Measuring angles and Segments Congruent segments are segments that have the same length. In the diagram, PQ = RS, so you can write PQ RS. This is read as “segment PQ is congruent to segment RS. ” Tick marks are used in a figure to show congruent segments. CH 1 -3 Geometry

Measuring angles and Segments A construction is a way of creating a figure that is precise. One way to make a geometric construction is to use a compass and straightedge. CH 1 -3 Geometry

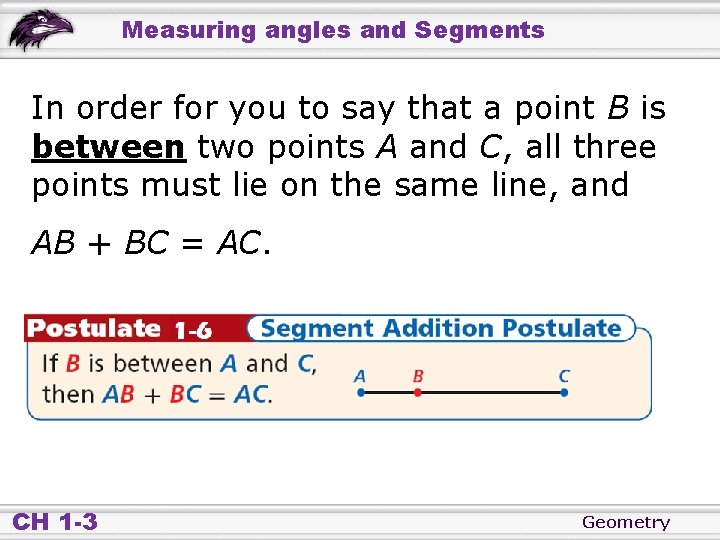
Measuring angles and Segments In order for you to say that a point B is between two points A and C, all three points must lie on the same line, and AB + BC = AC. CH 1 -3 Geometry

Measuring angles and Segments Example 2: Using the Segment Addition Postulate G is between F and H, FG = 6, and FH =11. Find GH. FH = FG + GH 11 = 6 + GH – 6 5 = GH CH 1 -3 Seg. Add. Postulate Substitute 6 for FG and 11 for FH. Subtract 6 from both sides. Simplify. Geometry

Measuring angles and Segments TEACH! Example 2 Y is between X and Z, XZ = 3, and XY = . Find YZ. Seg. Add. Postulate XZ = XY + YZ Substitute the given values. Subtract sides. CH 1 -3 from both Geometry

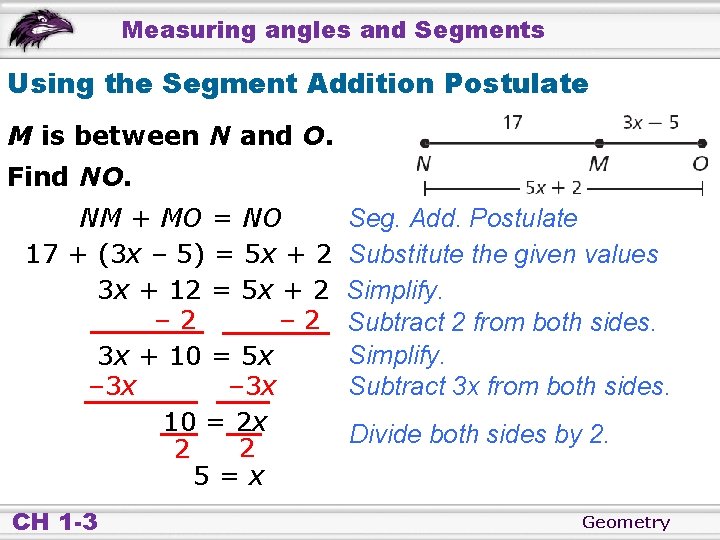
Measuring angles and Segments Using the Segment Addition Postulate M is between N and O. Find NO. NM + MO = NO 17 + (3 x – 5) = 5 x + 2 3 x + 12 = 5 x + 2 – 2 3 x + 10 = 5 x – 3 x 10 = 2 x 2 2 5=x CH 1 -3 Seg. Add. Postulate Substitute the given values Simplify. Subtract 2 from both sides. Simplify. Subtract 3 x from both sides. Divide both sides by 2. Geometry

Measuring angles and Segments Using the Segment Addition Postulate M is between N and O. Find NO. NO = 5 x + 2 = 5(5) + 2 = 27 CH 1 -3 Substitute 5 for x. Simplify. Geometry

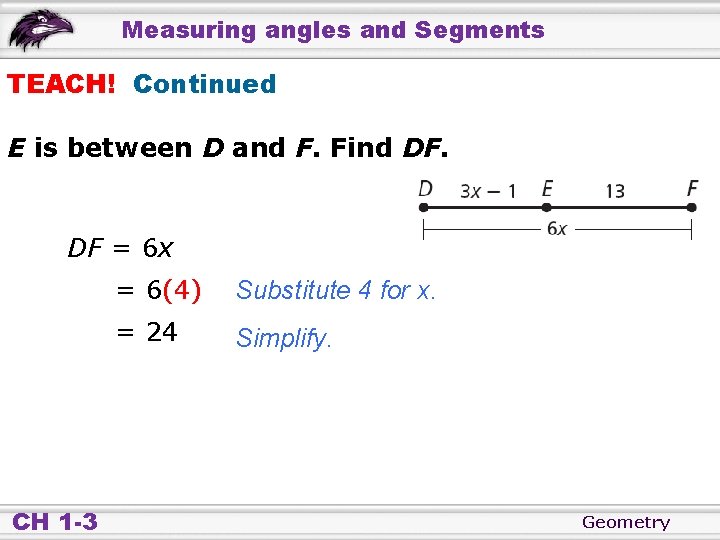
Measuring angles and Segments TEACH! E is between D and F. Find DF. DE + EF = DF (3 x – 1) + 13 = 6 x Seg. Add. Postulate Substitute the given values 3 x + 12 = 6 x – 3 x 12 = 3 x Subtract 3 x from both sides. 12 3 x 3 = 3 Divide both sides by 3. Simplify. 4=x CH 1 -3 Geometry

Measuring angles and Segments TEACH! Continued E is between D and F. Find DF. DF = 6 x CH 1 -3 = 6(4) Substitute 4 for x. = 24 Simplify. Geometry

Measuring angles and Segments The midpoint M of AB is the point that bisects, or divides, the segment into two congruent segments. If M is the midpoint of AB, then AM = MB. So if AB = 6, then AM = 3 and MB = 3. A CH 1 -3 M B Geometry

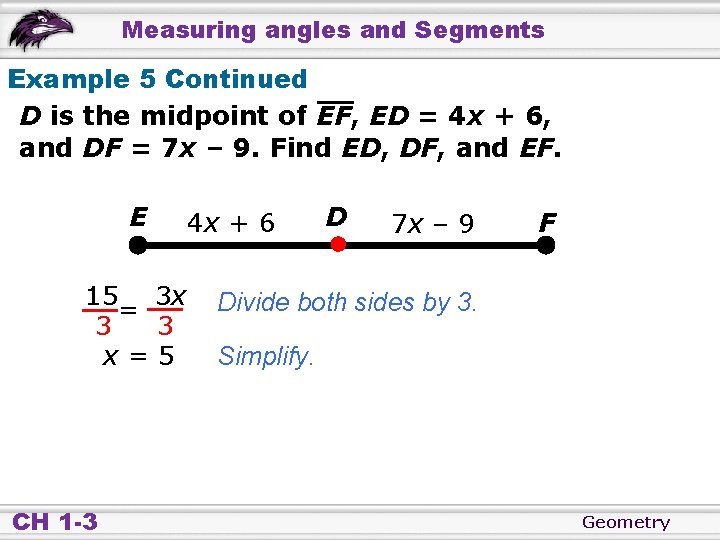
Measuring angles and Segments Example 5: Using Midpoints to Find Lengths D is the midpoint of EF, ED = 4 x + 6, and DF = 7 x – 9. Find ED, DF, and EF. E 4 x + 6 D 7 x – 9 F Step 1 Solve for x. D is the mdpoint. of EF. ED = DF 4 x + 6 = 7 x – 9 – 4 x 6 = 3 x – 9 +9 +9 15 = 3 x CH 1 -3 Substitute 4 x + 6 for ED and 7 x – 9 for DF. Subtract 4 x from both sides. Simplify. Add 9 to both sides. Simplify. Geometry

Measuring angles and Segments Example 5 Continued D is the midpoint of EF, ED = 4 x + 6, and DF = 7 x – 9. Find ED, DF, and EF. E 15 3 x = 3 3 x=5 CH 1 -3 4 x + 6 D 7 x – 9 F Divide both sides by 3. Simplify. Geometry

Measuring angles and Segments Example 5 Continued D is the midpoint of EF, ED = 4 x + 6, and DF = 7 x – 9. Find ED, DF, and EF. E 4 x + 6 D 7 x – 9 F Step 2 Find ED, DF, and EF. ED = 4 x + 6 DF = 7 x – 9 = 4(5) + 6 = 7(5) – 9 = 26 CH 1 -3 EF = ED + DF = 26 + 26 = 52 Geometry

Measuring angles and Segments TEACH! Example 5 S is the midpoint of RT, RS = – 2 x, and ST = – 3 x – 2. Find RS, ST, and RT. R – 2 x S – 3 x – 2 T Step 1 Solve for x. S is the mdpt. of RT. RS = ST – 2 x = – 3 x – 2 Substitute – 2 x for RS and – 3 x – 2 for ST. Add 3 x to both sides. +3 x x = – 2 CH 1 -3 Simplify. Geometry

Measuring angles and Segments TEACH! Example 5 Continued S is the midpoint of RT, RS = – 2 x, and ST = – 3 x – 2. Find RS, ST, and RT. R – 2 x S – 3 x – 2 T Step 2 Find RS, ST, and RT. RS = – 2 x = – 2(– 2) =4 CH 1 -3 ST = – 3 x – 2 = – 3(– 2) – 2 =4 RT = RS + ST =4+4 =8 Geometry

Measuring angles and Segments Lesson Quiz: Part I 1. M is between N and O. MO = 15, and MN = 7. 6. Find NO. 22. 6 2. S is the midpoint of TV, TS = 4 x – 7, and SV = 5 x – 15. Find TS, SV, and TV. 25, 50 3. Sketch, draw, and construct a segment congruent to CD. Check students' constructions CH 1 -3 Geometry

Measuring angles and Segments Lesson Quiz: Part II 4. LH bisects GK at M. GM = 2 x + 6, and GK = 24. Find x. 3 5. Tell whether the statement below is sometimes, always, or never true. Support your answer with a sketch. If M is the midpoint of KL, then M, K, and L are collinear. Always K M L CH 1 -3 Geometry

Measuring angles and Segments CH 1 -3 Geometry

Measuring angles and Segments Use the figure below for Exercises 1 -3. 1. Name the segments that form the triangle. RS, TR, ST 2. Name the rays that have point T as their endpoint. TO, TP, TR, TS 3. Explain how you can tell that no lines in the figure are parallel or skew. The three pairs of lines intersect, so they cannot be parallel or skew. CH 1 -3 Geometry

Measuring angles and Segments Use the figure for Exercises 4 and 5. 4. Name a pair of parallel planes. plane ABCD || plane XWQ 5. Name a line that is skew to XW. AC or BD CH 1 -3 Geometry