Lesson 1 2 Measurement of Segments and Angles










- Slides: 13

Lesson 1. 2 Measurement of Segments and Angles Objective: Measure segments, angles, classify angles by size, name the parts of a degree, recognize congruent angles and segments

Recap… Yesterday we touched briefly on measuring segments and angles, and classifying angles … Today, we are going to break down measuring angles into degrees, minutes, and seconds and discuss angle congruencies.

Recap Practice <B is acute. a. What are the restrictions on m<B? b. What are the restrictions on x? B (2 x + 14)°

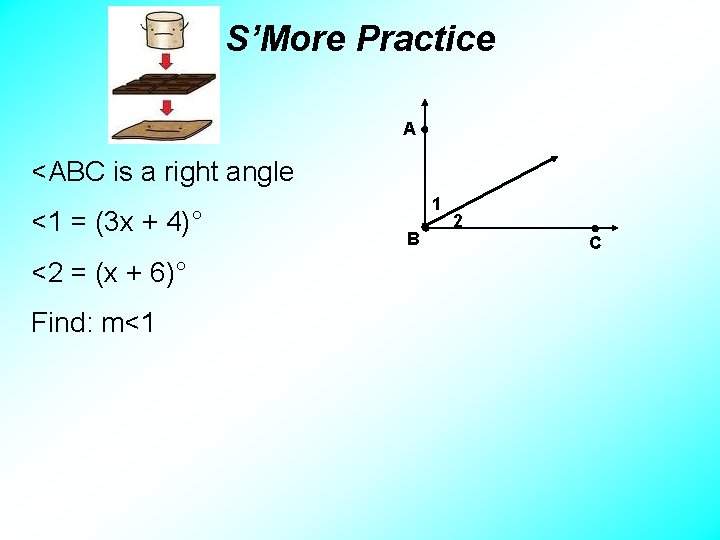
S’More Practice A <ABC is a right angle <1 = (3 x + 4)° <2 = (x + 6)° Find: m<1 1 B 2 C

Parts of a Degree Every hour of the day is divided into 60 minutes. Each minute is divided into 60 seconds. Similarly, each degree of an angle is divided into 60 minutes. And each minute of an angle is divided into 60 seconds. 60’ = 1° 60” = 1’

Practice… 1. 87½° = ½ of a degree is ½ of 60’= 30’ Answer: 87° 30’ 2. 60. 4° = 4/10 and 4/10 of 60 = 24 Answer: 60° 24’ 3. 90° = Answer: 89° 60’ 4. 180° = Answer: 179° 59’ 60”

Clock Handout Time! Important Notes: • A circle = 360°, and 360 ÷ 12 = 30° • Every 15 minutes the hour hand moves ¼ of 30° (that’s 7. 5°) One way to determine how many degrees the hour hand has moved is to calculate what fraction (out of 60 minutes) your minute hand is at. …. Let’s try this ….

Example #1: Find the measure of the angle formed by the hands of a clock at 11: 40 Between 8 and 9 = 30° Between 9 and 10 = 30° Between 10 and 11 = 30° Total = 90°

Example #1: Find the measure of the angle formed by the hands of a clock at 11: 40 Now we have to consider the 40 minutes. 40/60 = 2/3 (So the hour hand has moved 2/3 of the way between 11 and 12) 2/3 of 30° = 20° Final Answer: 90° + 20° = 110 °

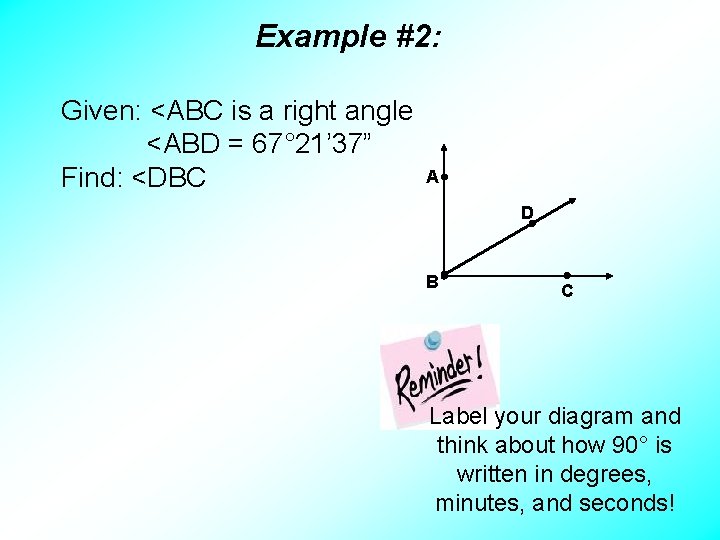
Example #2: Given: <ABC is a right angle <ABD = 67° 21’ 37” Find: <DBC A D B C Label your diagram and think about how 90° is written in degrees, minutes, and seconds!

Congruent Angles and Segments Def. Congruent ( ) angles are angles that have the same measure Def. Congruent ( ) segments are segments that have the same measure S 3 cm R 42° P 42° 3 cm A X B

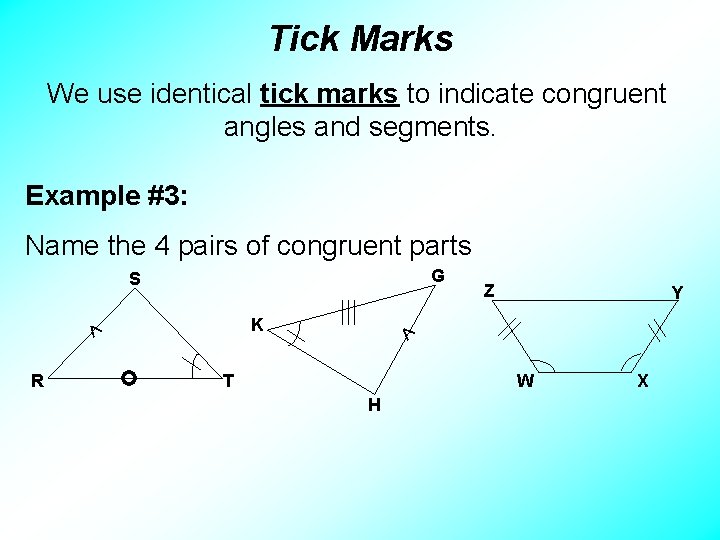
Tick Marks We use identical tick marks to indicate congruent angles and segments. Example #3: Name the 4 pairs of congruent parts G S Y K ^ ^ R Z T W H X

Homework Lesson 1. 2 Worksheet
 Lesson 1 hands on angles
Lesson 1 hands on angles Lesson 1 how to bisect segments and angles
Lesson 1 how to bisect segments and angles Lesson 1-1 measuring segments and angles
Lesson 1-1 measuring segments and angles Measuring angles and segments
Measuring angles and segments Vertically opposite angles properties
Vertically opposite angles properties Module 15 angles and segments in circles answer key
Module 15 angles and segments in circles answer key Lesson 8 solve for unknown angles
Lesson 8 solve for unknown angles Straight angle
Straight angle Proving statements about segments and angles
Proving statements about segments and angles Measuring segments
Measuring segments Tangent theorems
Tangent theorems Examples of opposite rays
Examples of opposite rays Lesson 2 segments and rays
Lesson 2 segments and rays 1-2 practice line segments and distance answer key
1-2 practice line segments and distance answer key