1 2 Measuringand and Constructing Segments 1 2

1 -2 Measuring and Constructing Segments Objectives Use length and midpoint of a segment.

1 -2 Measuring and Constructing Segments In order for you to say that a

1 -2 Measuring and Constructing Segments Example 3 A: Using the Segment Addition Postulate

1 -2 Measuring and Constructing Segments Example 3 B: Using the Segment Addition Postulate

1 -2 Measuring and Constructing Segments Example 3 B Continued M is between N

1 -2 Measuring and Constructing Segments Check It Out! Example 3 b E is

1 -2 Measuring and Constructing Segments Check It Out! Example 3 b Continued E

1 -2 Measuring and Constructing Segments The midpoint M of AB is the point

1 -2 Measuring and Constructing Segments Example 5: Using Midpoints to Find Lengths D

1 -2 Measuring and Constructing Segments Example 5 Continued D is the midpoint of

1 -2 Measuring and Constructing Segments Check It Out! Example 5 S is the

1 -2 Measuring and Constructing Segments Check It Out! Example 5 Continued S is

1 -2 Measuring and Constructing Segments Lesson Quiz: Part I 1. M is between

1 -2 Measuring and Constructing Segments Lesson Quiz: Part II 4. LH bisects GK

Slides: 16

Download presentation

1 -2 Measuringand and. Constructing. Segments 1 -2 Measuring Warm Up Lesson Presentation Lesson Quiz Holt Mc. Dougal Geometry

1 -2 Measuring and Constructing Segments Objectives Use length and midpoint of a segment. Construct midpoints and congruent segments. Holt Mc. Dougal Geometry

1 -2 Measuring and Constructing Segments In order for you to say that a point B is between two points A and C, all three points must lie on the same line, and AB + BC = AC. Holt Mc. Dougal Geometry

1 -2 Measuring and Constructing Segments Example 3 A: Using the Segment Addition Postulate G is between F and H, FG = 6, and FH = 11. Find GH. FH = FG + GH 11 = 6 + GH – 6 5 = GH Holt Mc. Dougal Geometry Seg. Add. Postulate Substitute 6 for FG and 11 for FH. Subtract 6 from both sides. Simplify.

1 -2 Measuring and Constructing Segments Example 3 B: Using the Segment Addition Postulate M is between N and O. Find NO. NM + MO = NO 17 + (3 x – 5) = 5 x + 2 3 x + 12 = 5 x + 2 – 2 3 x + 10 = 5 x – 3 x 10 = 2 x 2 2 5=x Holt Mc. Dougal Geometry Seg. Add. Postulate Substitute the given values Simplify. Subtract 2 from both sides. Simplify. Subtract 3 x from both sides. Divide both sides by 2.

1 -2 Measuring and Constructing Segments Example 3 B Continued M is between N and O. Find NO. NO = 5 x + 2 = 5(5) + 2 Substitute 5 for x. = 27 Simplify. Holt Mc. Dougal Geometry

1 -2 Measuring and Constructing Segments Check It Out! Example 3 b E is between D and F. Find DF. DE + EF = DF (3 x – 1) + 13 = 6 x 3 x + 12 = 6 x – 3 x 12 = 3 x 12 3 x = 3 3 4=x Holt Mc. Dougal Geometry Seg. Add. Postulate Substitute the given values Subtract 3 x from both sides. Simplify. Divide both sides by 3.

1 -2 Measuring and Constructing Segments Check It Out! Example 3 b Continued E is between D and F. Find DF. DF = 6 x = 6(4) Substitute 4 for x. = 24 Simplify. Holt Mc. Dougal Geometry

1 -2 Measuring and Constructing Segments The midpoint M of AB is the point that bisects, or divides, the segment into two congruent segments. If M is the midpoint of AB, then AM = MB. So if AB = 6, then AM = 3 and MB = 3. Holt Mc. Dougal Geometry

1 -2 Measuring and Constructing Segments Example 5: Using Midpoints to Find Lengths D is the midpoint of EF, ED = 4 x + 6, and DF = 7 x – 9. Find ED, DF, and EF. E 4 x + 6 Step 1 Solve for ED = DF 4 x + 6 = 7 x – 9 – 4 x D 7 x – 9 F x. D is the mdpt. of EF. Substitute 4 x + 6 for ED and 7 x – 9 for DF. Subtract 4 x from both sides. 6 = 3 x – 9 Simplify. +9 + 9 Add 9 to both sides. Simplify. 15 = 3 x Holt Mc. Dougal Geometry

1 -2 Measuring and Constructing Segments Example 5 Continued D is the midpoint of EF, ED = 4 x + 6, and DF = 7 x – 9. Find ED, DF, and EF. E 4 x + 6 15 3 x = 3 3 x=5 Holt Mc. Dougal Geometry D 7 x – 9 Divide both sides by 3. Simplify. F

1 -2 Measuring and Constructing Segments Example 5 Continued D is the midpoint of EF, ED = 4 x + 6, and DF = 7 x – 9. Find ED, DF, and EF. E 4 x + 6 D 7 x – 9 F Step 2 Find ED, DF, and EF. ED = 4 x + 6 DF = 7 x – 9 = 4(5) + 6 = 7(5) – 9 = 26 Holt Mc. Dougal Geometry EF = ED + DF = 26 + 26 = 52

1 -2 Measuring and Constructing Segments Check It Out! Example 5 S is the midpoint of RT, RS = – 2 x, and ST = – 3 x – 2. Find RS, ST, and RT. R – 2 x S – 3 x – 2 T Step 1 Solve for x. S is the mdpt. of RT. RS = ST – 2 x = – 3 x – 2 Substitute – 2 x for RS and – 3 x – 2 for ST. +3 x Add 3 x to both sides. x = – 2 Holt Mc. Dougal Geometry Simplify.

1 -2 Measuring and Constructing Segments Check It Out! Example 5 Continued S is the midpoint of RT, RS = – 2 x, and ST = – 3 x – 2. Find RS, ST, and RT. R – 2 x S – 3 x – 2 T Step 2 Find RS, ST, and RT. RS = – 2 x = – 2(– 2) =4 Holt Mc. Dougal Geometry ST = – 3 x – 2 = – 3(– 2) – 2 =4 RT = RS + ST =4+4 =8

1 -2 Measuring and Constructing Segments Lesson Quiz: Part I 1. M is between N and O. MO = 15, and MN = 7. 6. Find NO. 22. 6 2. S is the midpoint of TV, TS = 4 x – 7, and SV = 5 x – 15. Find TS, SV, and TV. 25, 50 3. Sketch, draw, and construct a segment congruent to CD. Check students' constructions Holt Mc. Dougal Geometry

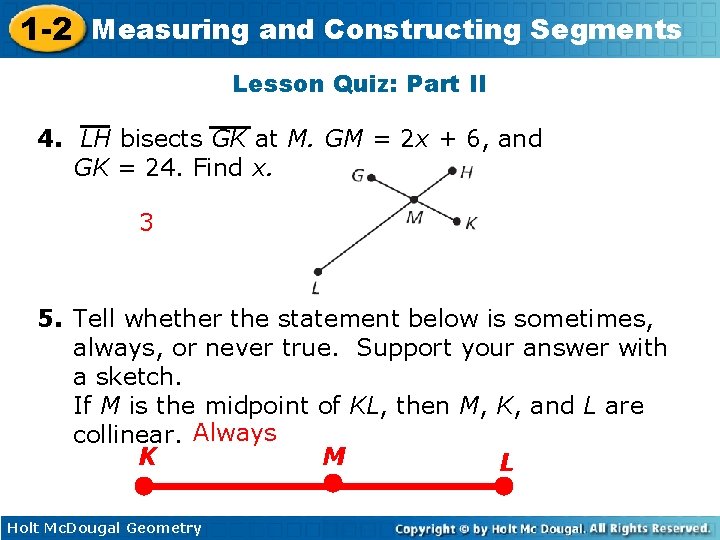
1 -2 Measuring and Constructing Segments Lesson Quiz: Part II 4. LH bisects GK at M. GM = 2 x + 6, and GK = 24. Find x. 3 5. Tell whether the statement below is sometimes, always, or never true. Support your answer with a sketch. If M is the midpoint of KL, then M, K, and L are collinear. Always K M L Holt Mc. Dougal Geometry