Lecture 16 Streams continue Infinite Streams 16 1

Lecture 16 Streams continue Infinite Streams 16 שיעור - מבוא מורחב 1

Finite Streams (define (stream-enumerate-interval low high) (if (> low high) the-empty-stream (cons-stream low (stream-enumerate-interval (+ low 1) high)))) (define s (stream-enumerate-interval 1 100000)) 16 שיעור - מבוא מורחב 2

Infinite streams Since streams are delayed, we are not limited to finite streams!! Some objects are more naturally infinite 16 שיעור - מבוא מורחב 3

The integers (define (integers-from n) (cons-stream n (integers-from (+ n 1)))) (define integers (integers-from 1)) 16 שיעור - מבוא מורחב 4

Integers not divisible by 7 (define (divisible? x y) (= (remainder x y) 0)) (define no-sevens (stream-filter (lambda (x) (not (divisible? x 7))) integers)) (stream-ref no-sevens 100) 117 16 שיעור - מבוא מורחב 5

Fibonacci sequence (define (fib-seq-from a b) (cons-stream a (fib-seq-from b (+ a b)))) (define fib-seq (fib-seq-from 0 1)) 16 שיעור - מבוא מורחב 6

Fibonacci sequence Ø(define (fib-seq-from a b) (cons-stream a (fib-seq-from b (+ a b)))) Ø(define fib-seq (fib-seq-from 0 1)) Ø fib-seq (0. #<struct: promise>[fib-seq-from 1 1]) Ø(stream-ref (stream-ref (stream-ref 2 fib-seq 3) (stream-cdr fib-seq) 2) (fib-seq-from 1 1) 2) (cons 1 (delay (fib-seq-from 1 2))) 2) (stream-cdr (cons 1 (delay (fib-seq-from 1 2)) 1) (fib-seq-from 1 2) 1) (cons 1 (delay (fib-seq from 2 3))) 1) (stream-cdr (cons 1 (delay (fib-seq-from 2 3)))) 0) (fib-seq-from 2 3) 0) (cons 2 (delay (fib-seq-from 3 5))) 0) 16 שיעור - מבוא מורחב 7

Finding all the primes using the sieve of Eratosthenes 2 3 X 4 5 X 6 7 X 8 X 9 10 XX 11 12 XX 13 XX 14 15 XX 16 XX 17 18 XX 19 20 XX XX 21 22 XX 23 24 XX 25 XX 26 XX 27 XX XX 28 29 30 XX 31 XX 32 XX 33 XX 34 XX 35 XX 36 37 XX 38 XX 39 XX 40 41 XX 42 43 XX 44 XX 45 XX 46 47 XX 48 XX 49 XX 50 XX 51 XX 52 53 XX 54 XX 55 XX 56 XX 57 XX 58 59 XX 60 61 62 XX 63 XX 64 XX 65 XX 66 XX 67 68 XX 69 XX 60 XX 71 72 XX 73 74 XX 75 XX 76 XX XX 77 78 XX 79 80 XX XX 81 XX 82 83 XX 84 XX 85 XX 86 XX 87 XX 88 89 XX 90 XX 91 XX 92 XX 93 XX 94 XX 95 XX 96 97 XX 98 XX 99 XX 100 16 שיעור - מבוא מורחב 8

The sieve of Eratosthenes using streams (define (sieve str) (cons-stream (stream-car str) (sieve (stream-filter (lambda (x) (not (divisible? x (stream-car str)))) (stream-cdr str))))) (define primes (sieve (stream-cdr integers))) 16 שיעור - מבוא מורחב 9

The integers, again (implicit version) We saw the definition: (define (integers-from n) (cons-stream n (integers-from (+ n 1)))) (define integers (integers-from 1)) An alternative definition: (define integers (cons-stream 1 (stream-map (lambda (x) (+ x 1)) integers)) (integers) integers 1 2. . . 1 2 3. . . input to stream-map result: element + 1 16 שיעור - מבוא מורחב 10

The integers – another way (define ones (cons-stream 1 ones)) (define integers (cons-stream 1 (add-streams ones integers)) (define (add-streams s 1 s 2) (stream-map + s 1 s 2)) A direct implementation of add-streams: (define (add-streams s 1 s 2) (cons-stream (+ (stream-car s 1) (stream-car s 2)) (add-streams (stream-cdr s 1) (stream-cdr s 2)))) 16 שיעור - מבוא מורחב 11

Implicit definition of the Fibonacci numbers (define fibs (cons-stream 0 (cons-stream 1 (add-streams (stream-cdr fibs)))) 1 1 2 3 0 1 1 2 3 (stream-cdr fibs) fibs 16 שיעור - מבוא מורחב 12

More implicit definitions (define (scale-stream str factor) (stream-map (lambda (x) (* x factor)) str) (define double (cons-stream 1 (scale-stream double 2))) double (scale-factor double 2) 1 2 4 8 16 שיעור - מבוא מורחב 8 13

The stream of primes – another way (define primes (cons-stream 2 (stream-filter prime? (integers-from 3)))) (define (prime? n) (define (iter ps) (cond ((> (square (stream-car ps)) n) #t) ((divisible? n (stream-car ps)) #f) (else (iter (stream-cdr ps))))) (iter primes) • A recursive definition. • Works because the primes needed to check primality of the next number are always ready. 16 שיעור - מבוא מורחב 14

Formulating iterations as stream processes (define (sqrt x) (define (good-enough? guess) (< (abs (- (square guess) x)) 0. 001)) (define (sqrt-improve guess) (average guess (/ x guess))) (define (sqrt-iter guess) (if (good-enough? guess) guess (sqrt-iter (sqrt-improve guess)))) (sqrt-iter 1. 0)) 16 שיעור - מבוא מורחב 15

Formulating iterations as stream processes (cont’d) (define (sqrt-stream x) (define (good-enough? guess) (< (abs (- (square guess) x)) 0. 001)) (define (sqrt-improve guess x) (average guess (/ x guess))) (define guesses (cons-stream 1. 0 (stream-map (lambda (guess) (sqrt-improve guess x)) guesses))) (stream-car (stream-filter ________________________ (lambda(x) (good-enough? x)) ________________________ guesses))) ________________________) 16 שיעור - מבוא מורחב 16

Formulating iterations as stream processes (Cont. ) 4 1 1 1 = 1 - 3 + 5 - 7 . . . (define (pi-summands n) (cons-stream (/ 1. 0 n) (stream-map - (pi-summands (+ n 2))))) (pi-summands 1) (1 (stream-map - (pi-summands 3))) (1 (stream-map - (1/3 (stream-map - (pi-summands 5)))) (1 -1/3 +1/5 (stream-map - (pi-summands 7))))) 16 שיעור - מבוא מורחב 17

Replacing state variables with streams (Cont. ) 4 = 1 - 1 3 + 1 5 1 - 7 . . . (define (pi-summands n) (cons-stream (/ 1. 0 n) (stream-map - (pi-summands (+ n 2))))) (define pi-stream (scale-stream (partial-sums (pi-summands 1)) 4)) (display-stream pi-stream) 4. 2. 6666 3. 4666 2. 8952 3. 3396 2. 9760 S = S 0, S 0+S 1+S 2, … converges very slowly! 16 שיעור - מבוא מורחב 18

Speeding up convergence (define (euler-transform s) (let ((s 0 (stream-ref s 0)) (s 1 (stream-ref s 1)) (s 2 (stream-ref s 2))) (cons-stream (- s 2 (/ (square (- s 2 s 1)) (+ s 0 (* -2 s 1) s 2))) (euler-transform (stream-cdr s))))) S’n = Sn+1 - (Sn+1 - Sn)2 Sn-1 - 2 Sn + Sn+1 16 שיעור - מבוא מורחב 19

Speeding Up Convergence (Cont. ) (display-stream (euler-transform pi-stream)) 3. 1666 3. 1333 3. 1452 3. 1396 3. 1427 3. 1408 16 שיעור - מבוא מורחב 20

Speeding up convergence even further (define (make-tableau transform s) (cons-stream s (make-tableau transform (transform s)))) produces a stream of streams: s, (transform s), (transform s)). . . S 00 S 01 S 02 S 03 … S 10 S 11 S 12 … S 20 S 21 … S 30 … 16 שיעור - מבוא מורחב 21

Speeding up convergence even further (Cont. ) (define (accelerated-sequence transform s) (stream-map stream-car (make-tableau transform s))) S 00 S 01 S 02 S 03. . S 10 S 11 S 12. . . S 20 S 21 , . . . (display-stream (accelerated-sequence euler-transform pi-stream)) 4. 3. 1666… 3. 1421… 3. 1415… 16 שיעור - מבוא מורחב 22

Infinite streams of pairs Want to produce the stream of pairs of all integers (i, j) with i j and bind it to int-pairs. Abstraction: Let’s solve an even more general problem. Given two streams S=(S 1, S 2. . . ) T=(T 1, T 2. . . ) Consider the infinite rectangular array (S 1, T 1) (S 1, T 2) (S 1, T 3). . . (S 2, T 1) (S 2, T 2) (S 2, T 3). . . (S 3, T 1) (S 3, T 2) (S 3, T 3). . . 16 שיעור - מבוא מורחב 23

Infinite streams of pairs (S 1, T 1) (S 1, T 2) (S 1, T 3). . . (S 2, T 1) (S 2, T 2) (S 2, T 3). . . (S 3, T 1) (S 3, T 2) (S 3, T 3). . . Wish to produce all pairs that lie on or above the diagonal: j (S 1, T 1) (S 1, T 2) (S 1, T 3). . . (S 2, T 2) (S 2, T 3). . . i (S 3, T 3). . . If S and T are both the integers then this would be int-pairs 16 שיעור - מבוא מורחב 24

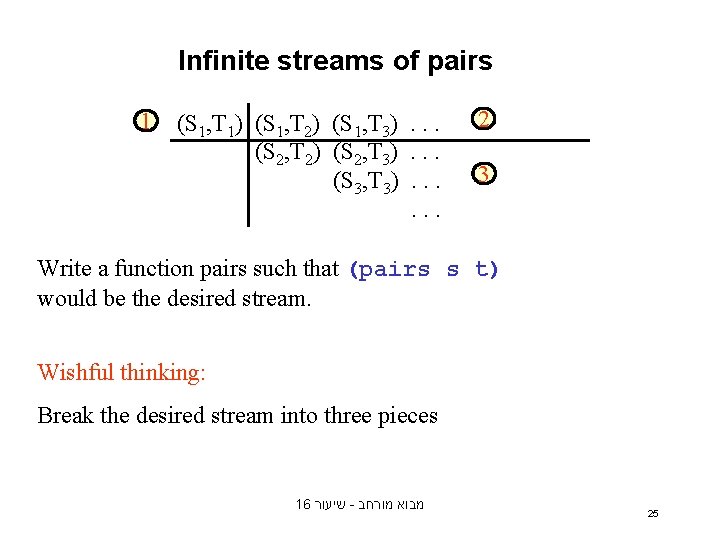
Infinite streams of pairs 1 (S 1, T 1) (S 1, T 2) (S 1, T 3). . . (S 2, T 2) (S 2, T 3). . . (S 3, T 3). . . 2 3 Write a function pairs such that (pairs s t) would be the desired stream. Wishful thinking: Break the desired stream into three pieces 16 שיעור - מבוא מורחב 25

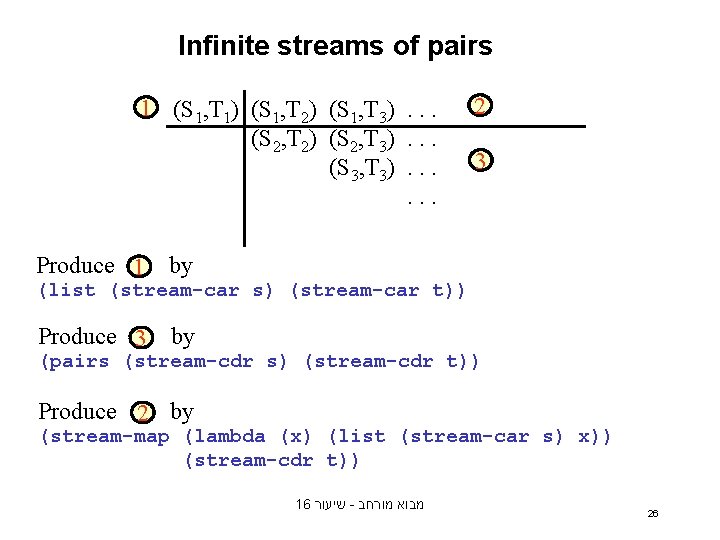
Infinite streams of pairs 1 (S 1, T 1) (S 1, T 2) (S 1, T 3). . . (S 2, T 2) (S 2, T 3). . . (S 3, T 3). . . 2 3 Produce 1 by (list (stream-car s) (stream-car t)) Produce 3 by (pairs (stream-cdr s) (stream-cdr t)) Produce 2 by (stream-map (lambda (x) (list (stream-car s) x)) (stream-cdr t)) 16 שיעור - מבוא מורחב 26

Infinite streams of pairs (define (pairs s t) (cons-stream 1 (list (stream-car s) (stream-car t)) (combine-in-some-way 2 (stream-map (lambda (x) (list (stream-car s) x)) (stream-cdr t)) 3 (pairs (stream-cdr s) (stream-cdr t))))) How do we combine? (define (stream-append s 1 s 2) (if (stream-null? s 1) s 2 (cons-stream (stream-car s 1) (stream-append (stream-cdr s 1) s 2)))) 16 שיעור - מבוא מורחב 27

Infinite streams of pairs (cont’d) (define int-pairs (pairs integers)) Ø(display-stream int-pairs) (1 1) (1 2) (1 3) (1 4) … will never produce a pair with first component different from 1 !! stream-append does not work when the first stream in infinite We want to be able to produce any pair by applying stream-cdr enough times. 16 שיעור - מבוא מורחב 28

Infinite streams of pairs (cont’d) (define (pairs s t) (cons-stream (list (stream-car s) (stream-car t)) (interleave (stream-map (lambda (x) (list (stream-car s) x)) (stream-cdr t)) (pairs (stream-cdr s) (stream-cdr t))))) (define (interleave s 1 s 2) (if (stream-null? s 1) s 2 (cons-stream (stream-car s 1) (interleave s 2 (stream-cdr s 1))))) 16 שיעור - מבוא מורחב 29

Infinite streams of pairs (cont’d) (define (pairs s t) (cons-stream (list (stream-car s) (stream-car t)) (interleave (stream-map (lambda (x) (list (stream-car s) x)) (stream-cdr t)) (pairs (stream-cdr s) (stream-cdr t))))) Ø(define int-pairs (pairs integers)) Ø(display-stream int-pairs) (1 1) (1 2) (2 2) (1 3) (2 3) (1 4) (3 3) (1 5)… 16 שיעור - מבוא מורחב 30

Isn’t there a simpler solution? Produce 1 (S 1, T 1) (S 1, T 2) (S 1, T 3). . . (S 2, T 2) (S 2, T 3). . . (S 3, T 3). . . 1 by 2 (stream-map (lambda (x) (list (stream-car s) x)) t) Produce 2 by (pairs (stream-cdr s) (stream-cdr t)) (define (pairs s t) (interleave (stream-map (lambda (x) (list (stream-car s) x)) t) (pairs (stream-cdr s) (stream-cdr t))))) 16 שיעור - מבוא מורחב 31

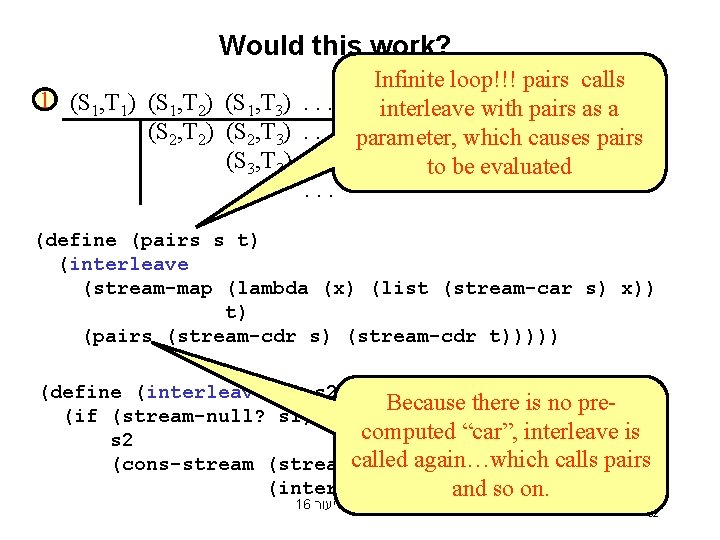
Would this work? Infinite loop!!! pairs calls 1 (S 1, T 1) (S 1, T 2) (S 1, T 3). . . interleave with pairs as a (S 2, T 2) (S 2, T 3). . . parameter, which causes pairs 2 (S 3, T 3). . . to be evaluated. . . (define (pairs s t) (interleave (stream-map (lambda (x) (list (stream-car s) x)) t) (pairs (stream-cdr s) (stream-cdr t))))) (define (interleave s 1 s 2) Because there is no pre(if (stream-null? s 1) computed “car”, interleave is s 2 called s 1) again…which calls pairs (cons-stream (stream-car (interleave s 2 (stream-cdr s 1))))) and so on. 16 שיעור - מבוא מורחב 32

The generalized stream-map (multiple streams) (define (stream-map proc. argstreams) (if (or (null? argstreams) (stream-null? (car argstreams))) the-empty-stream (cons-stream (apply proc (map stream-car argstreams)) (apply stream-map (cons proc (map stream-cdr argstreams)))))) • Does it work for finite/infinite streams? • What if some are finite and others infinite? • What about finite streams with different lengths? 16 שיעור - מבוא מורחב 33