Ladders Couches and Envelopes An old technique gives

Ladders, Couches, and Envelopes An old technique gives a new approach to an old problem Dan Kalman American University Fall 2007

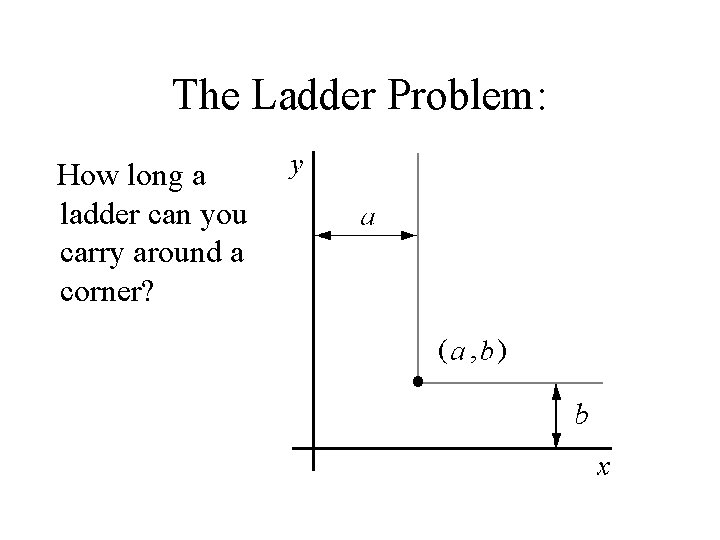
The Ladder Problem: How long a ladder can you carry around a corner?

The Traditional Approach • Reverse the question • Instead of the longest ladder that will go around the corner … • Find the shortest ladder that will not

A Direct Approach • Why is this reversal necessary? • Look for a direct approach: find the longest ladder that fits • Conservative approach: slide the ladder along the walls as far as possible • Let’s look at a mathwright simulation

About the Boundary Curve • Called the envelope of the family of lines • Nice calculus technique to find its equation • Technique used to be standard topic • Well known curve (astroid, etc. ) • Gives an immediate solution to the ladder problem

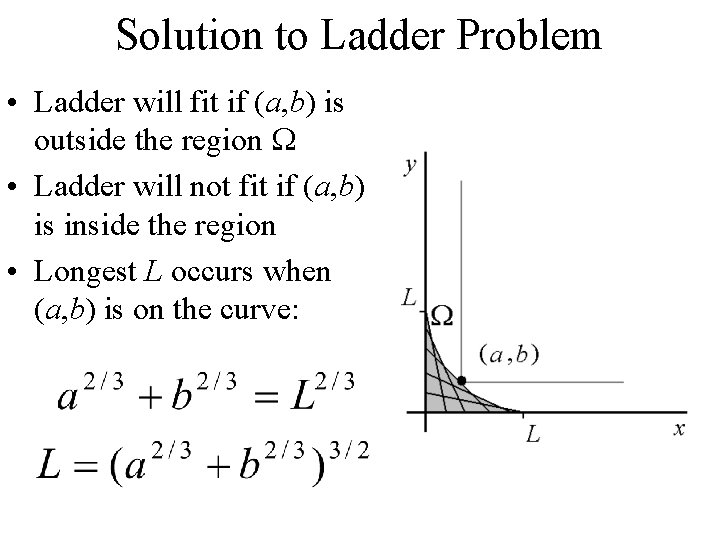
Solution to Ladder Problem • Ladder will fit if (a, b) is outside the region W • Ladder will not fit if (a, b) is inside the region • Longest L occurs when (a, b) is on the curve:

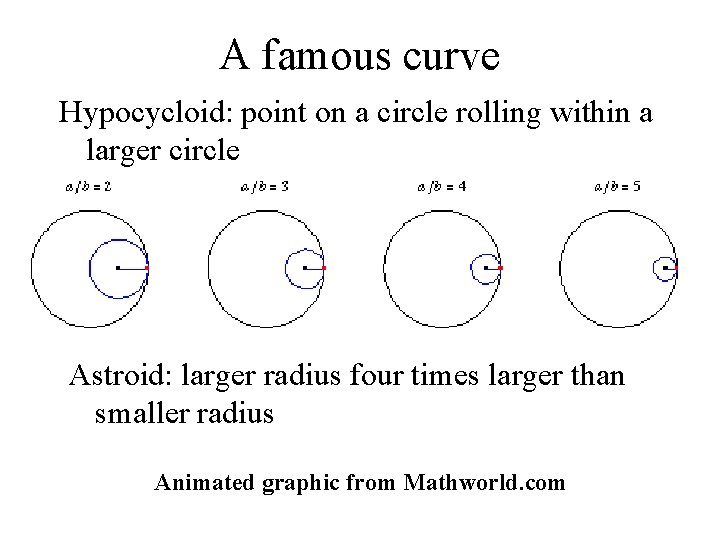
A famous curve Hypocycloid: point on a circle rolling within a larger circle Astroid: larger radius four times larger than smaller radius Animated graphic from Mathworld. com

Trammel of Archimedes

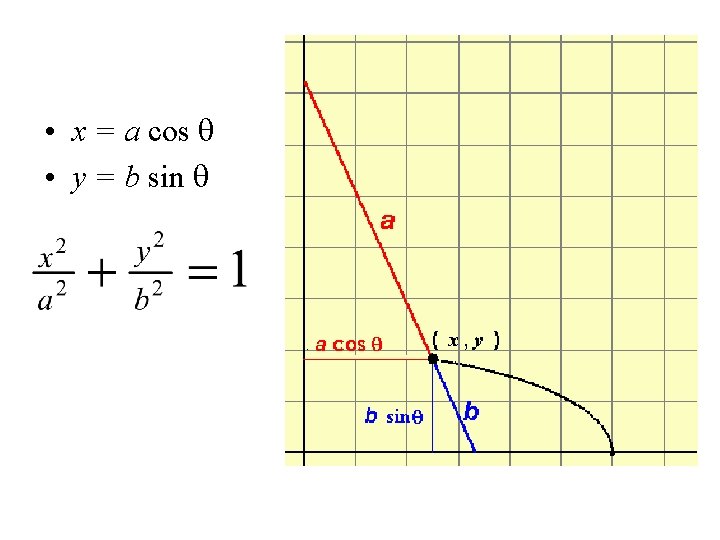
Alternate View • Ellipse Model: slide a line with its ends on the axes, let a fixed point on the line trace a curve • The length of the line is the sum of the semi major and minor axes

• x = a cos q • y = b sin q

Family of Ellipses § Paint an ellipse with every point of the ladder § Family of ellipses with sum of major and minor axes equal to length L of ladder § These ellipses sweep out the same region as the moving line § Same envelope

Animated graphic from Mathworld. com

Finding the Envelope Family of curves given by F(x, y, a) = 0 For each a the equation defines a curve Take the partial derivative with respect to a Use the equations of F and Fa to eliminate the parameter a • Resulting equation in x and y is the envelope • •

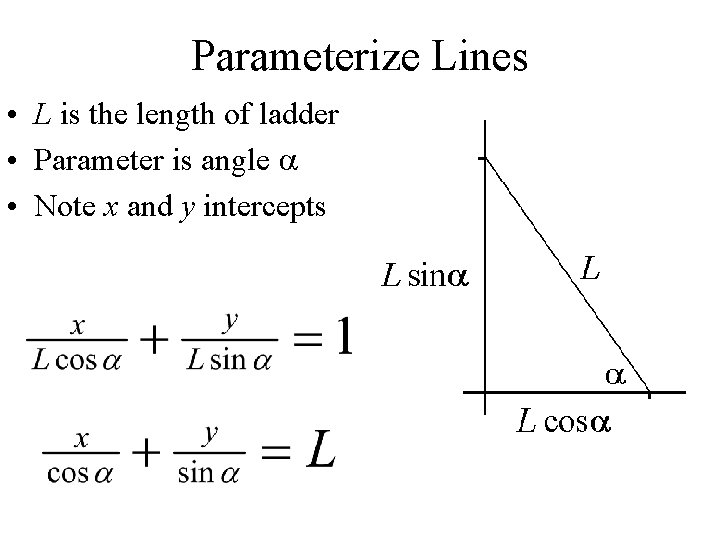
Parameterize Lines • L is the length of ladder • Parameter is angle a • Note x and y intercepts

Find Envelope

Find Envelope

Another sample family of curves and its envelope

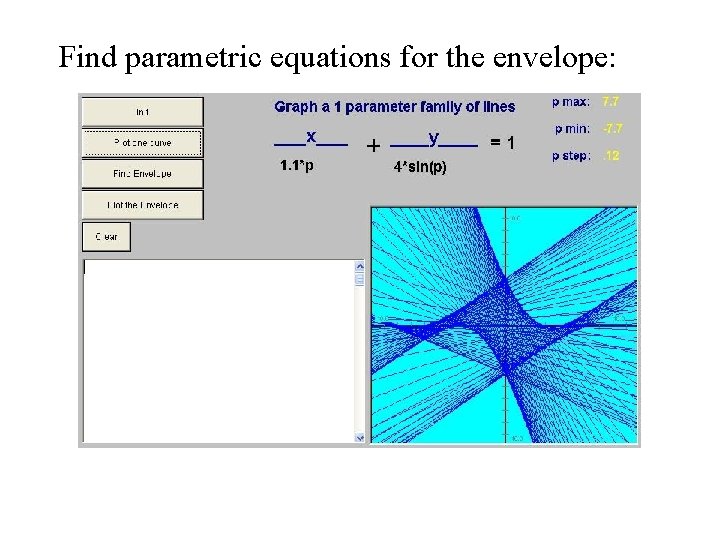
Find parametric equations for the envelope:

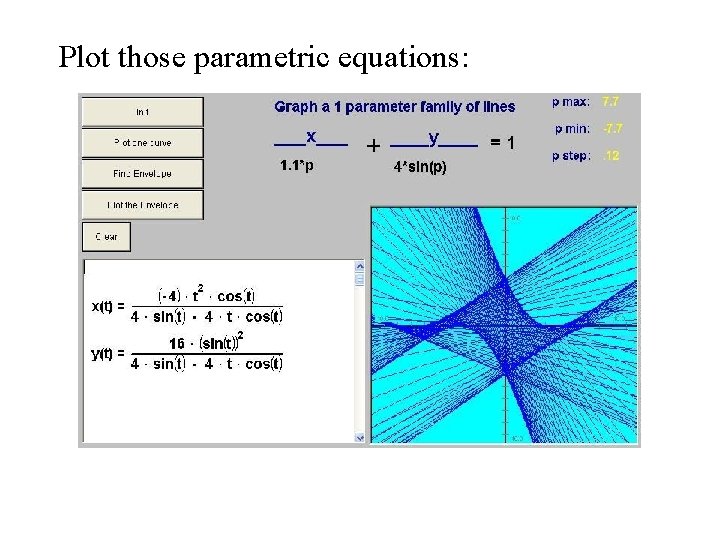
Plot those parametric equations:

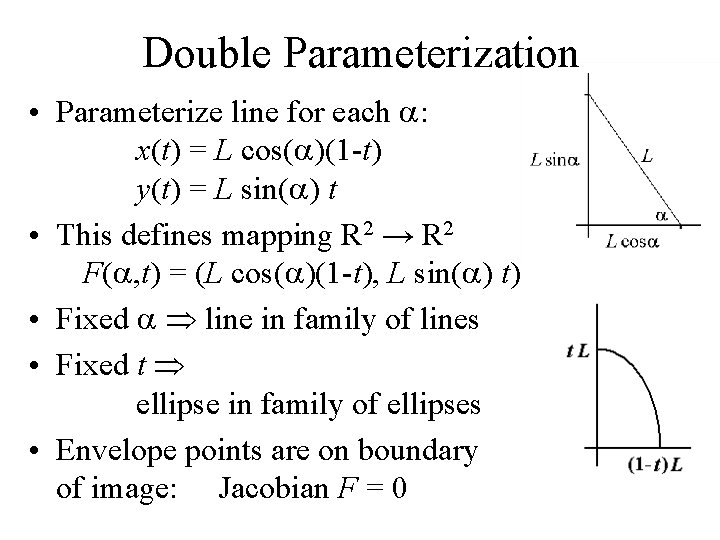
Double Parameterization • Parameterize line for each a: x(t) = L cos(a)(1 -t) y(t) = L sin(a) t • This defines mapping R 2 → R 2 F(a, t) = (L cos(a)(1 -t), L sin(a) t) • Fixed a line in family of lines • Fixed t ellipse in family of ellipses • Envelope points are on boundary of image: Jacobian F = 0

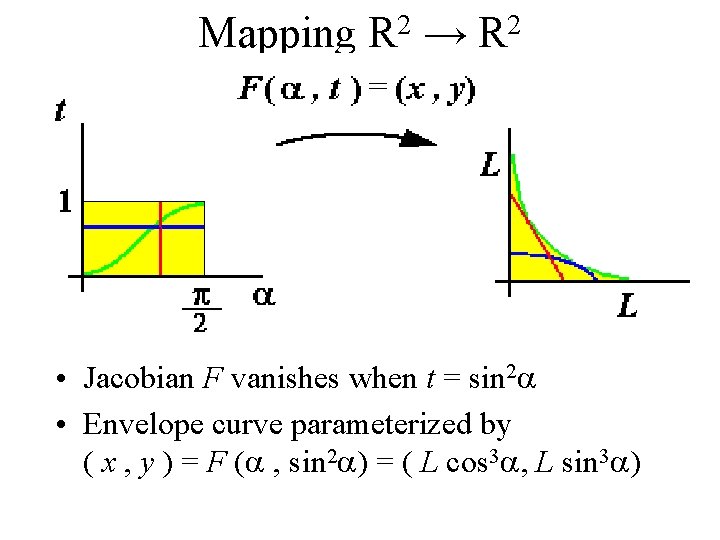
Mapping R 2 → R 2 • Jacobian F vanishes when t = sin 2 a • Envelope curve parameterized by ( x , y ) = F (a , sin 2 a) = ( L cos 3 a, L sin 3 a)

History of Envelopes • In 1940’s and 1950’s, some authors claimed envelopes were standard topic in calculus • Nice treatment in Courant’s 1949 Calculus text • Some later appearances in advanced calculus and theory of equations books • No instance in current calculus books I checked • Not included in Thomas (1 st ed. ) • Still mentioned in context of differential eqns • What happened to envelopes?

Another Approach • Already saw two approaches • Intersection Approach: intersect the curves for parameter values a and a + h • Take limit as h goes to 0 • Envelope is locus of intersections of neighboring curves • Neat idea, but …

Example: No intersections • Start with given ellipse • At each point construct the osculating circle (radius = radius of curvature) • Original ellipse is the envelope of this family of circles • Neighboring ellipses are disjoint!

More Pictures: Family of Osculating Circles for an Ellipse

Variations on the Ladder Problem

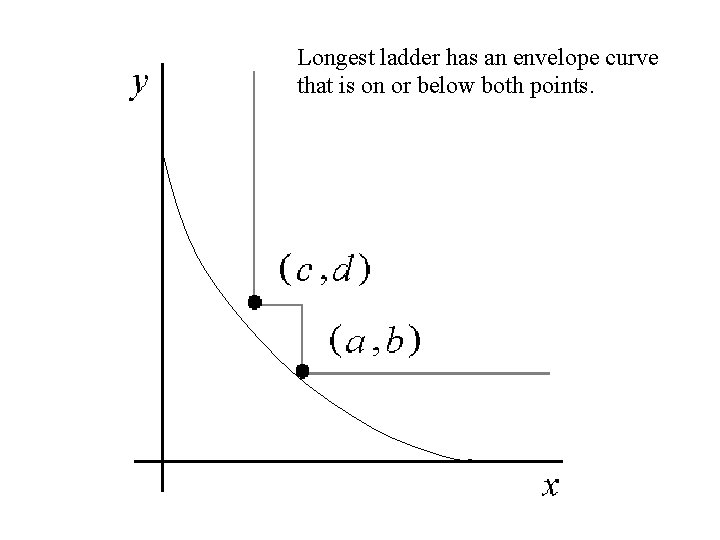
Longest ladder has an envelope curve that is on or below both points.

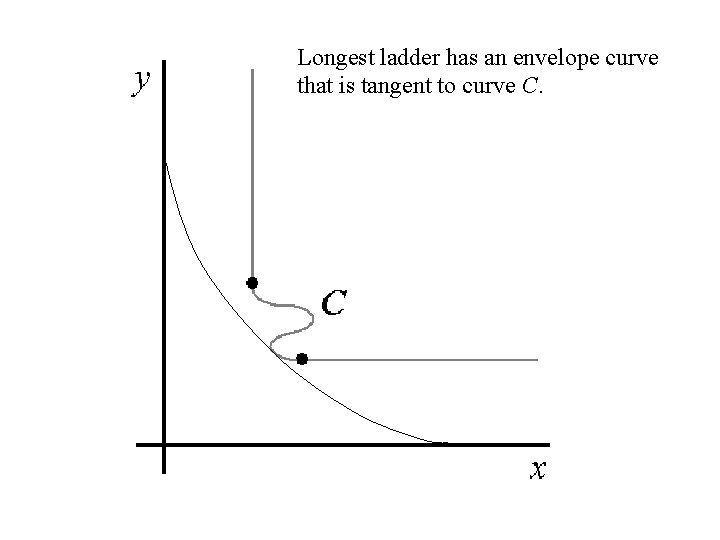
Longest ladder has an envelope curve that is tangent to curve C.

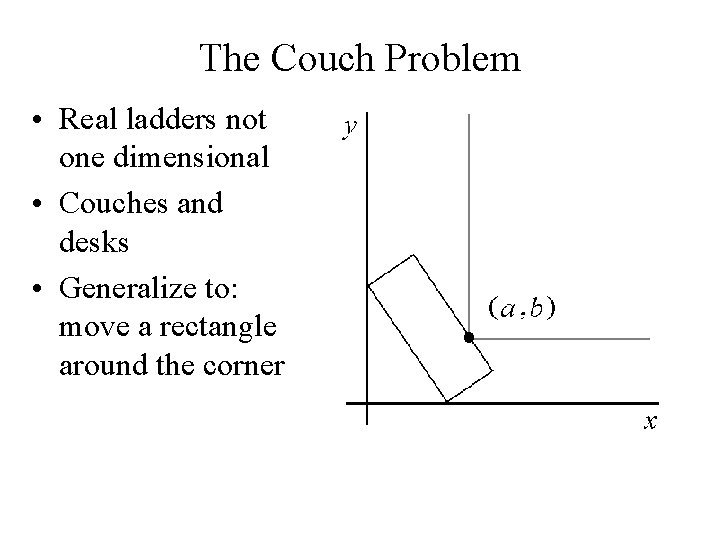
The Couch Problem • Real ladders not one dimensional • Couches and desks • Generalize to: move a rectangle around the corner

Couch Problem Results • Lower edge of couch follows same path as the ladder • Upper edge traces a parallel curve C (Not a translate) • At maximum, corner point is on C • Theorem: Envelope of parallels of curves is the parallel of the envelope of the curves • Theorem: At max length, circle centered at corner point is tangent to original envelope E (the astroid)

Good News / Bad News • Cannot solve couch problem symbolically • Requires solving a 6 th degree polynomial • It is possible to parameterize an infinite set of problems (corner location, width) with exact rational solutions • Example: Point (7, 3. 5); Width 1. Maximum length is 12. 5

More • Math behind envelope algorithm is interesting • Different formulations of envelope: boundary curve? Tangent to every curve in family? Neighboring curve intersections? • Ladder problem is related to Lagrange Multipliers and Duality • See my paper on the subject