Kartleggingsomrder av sentrale kjennetegn 1 Telling og gruppering

Kartleggingsområder av sentrale kjennetegn 1. Telling og gruppering 2. Antallsoppfatning, subitizing og visuelle mønstre 3. Tallsymbolkunnskap (lese og skrive tall) 4. De første regneprinsipper og avledete faktastrategier 5. Plassverdi 6. Automatiserte regnefakta 7. Problemløsning 8. Planlegging og konsentrasjon RA 200109 Innføring i matematikkvansker 3 1

Tegn 2: Antallsoppfatning. A: Subitising, rask oppfatning av små antall • Butterworths Number Module: få uker gamle babyer kan addere og subtrahere små mengder. Mener vi er født med et spesielt nettverk som har to viktige funksjoner : - kategorisere verden i antall (i det minste små antall) - ordne antall etter størrelse. (Johnsen 2004) • Testes ved hurtig å bestemme antall prikker. Poenget er ikke å trenge og telle små antall opp til 4. (Butterworth 2003, MIO, KATS 2, AT 1. 4) • Testes også hurtigheten av å finne det ”største” tallet i matematisk forstand med visuell forvirringsfaktor. 8 RA 200109 5 Innføring i matematikkvansker 3 2

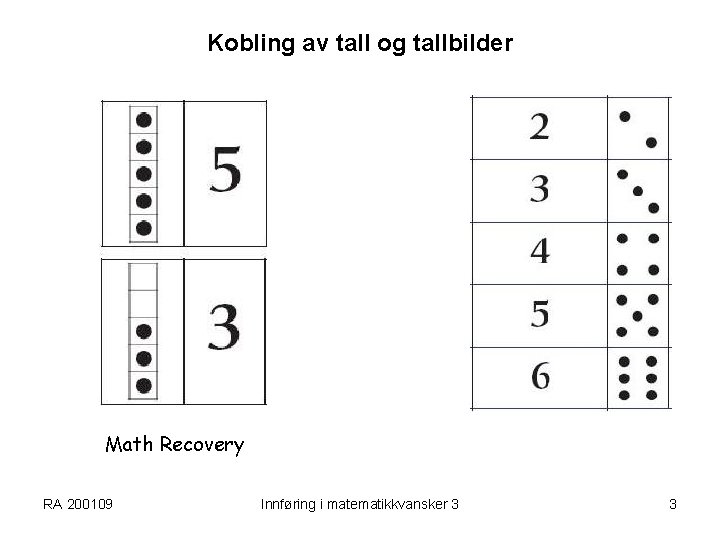
Kobling av tall og tallbilder Math Recovery RA 200109 Innføring i matematikkvansker 3 3

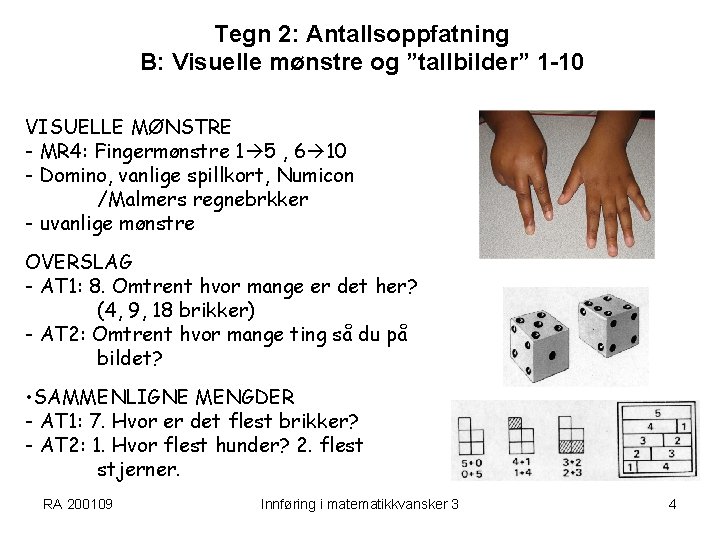
Tegn 2: Antallsoppfatning B: Visuelle mønstre og ”tallbilder” 1 -10 VISUELLE MØNSTRE - MR 4: Fingermønstre 1 5 , 6 10 - Domino, vanlige spillkort, Numicon /Malmers regnebrkker - uvanlige mønstre OVERSLAG - AT 1: 8. Omtrent hvor mange er det her? (4, 9, 18 brikker) - AT 2: Omtrent hvor mange ting så du på bildet? • SAMMENLIGNE MENGDER - AT 1: 7. Hvor er det flest brikker? - AT 2: 1. Hvor flest hunder? 2. flest stjerner. RA 200109 Innføring i matematikkvansker 3 4

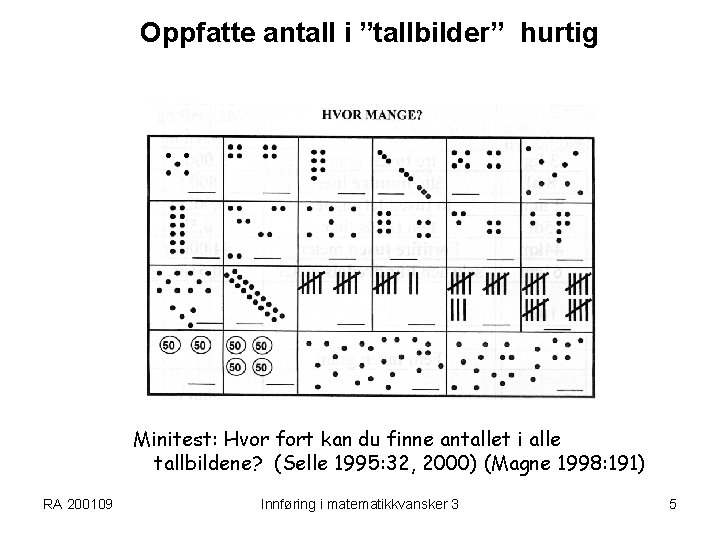
Oppfatte antall i ”tallbilder” hurtig Minitest: Hvor fort kan du finne antallet i alle tallbildene? (Selle 1995: 32, 2000) (Magne 1998: 191) RA 200109 Innføring i matematikkvansker 3 5

Tiltak i rask visuell oppfatning Adlers teorigrunnlagfra: Adler, Björn (2005). Vad er dyskalkyli? . www. dyskalkyli. nu - trening ved spesifikke m. v. bør først og fremst skje alene, det er mest effektivt siden det ikke er en enhetlig gruppe. s 109 - 20 -30 min hver dag for seg selv - kompensere med hjelpemidler i klassen - ominnlæring / overlæring av (s. 111): * rask lesing og skriving av tall (høyre/venstre? ) * rask utføring av enkle regneoperasjoner * raskt å se tallets verdi i relasjon til andre * raskt å kunne se hvilken regnemåte som er riktig å bruke * raskt kjenne igjen regnesymbolene * raskt se forskjell på størrelsen av geometriske figurer * raskt regne om mellom forskjellige målenheter - arbeide med automatisering s. 114, prbl med framhenting av informasjon, bør skje alene i korte økte RA 200109 Innføring i matematikkvansker 3 6

Kjennetegn 3: Tallkjennskap, symboloppfatning • AT 1: 1. Si, skriv og les noen tall, 2. Hvor ser du tall? 6. Hvilket tall? (vis tallkort, fra bilde til tall) • AT 2: 4. Skriv tallet fire. 5. Skriv sju. 6. Ring rundt fem Persepsjonsvansker kan gi feiloppfatninger av sifrene og gi leseog skriveproblemer hos noen få, men det kommer utenfor temaet her (speilvending, skriveretning). Dette er ikke tema i Alle teller, men mer i nevropsykologisk vinkling (Adler). RA 200109 Innføring i matematikkvansker 3 7

Kjennetegn 4: De første regneprinsipper; overslag og avledete faktastrategier TESTPROBLEMATIKK: • At barn teller betyr ikke nødvendigvis at de ikke kan noen regnefakta som de kan tenke ut i fra. • Kontekst betyr mye for hvordan barn svarer • Barn kan ikke alltid selv si hvordan de har tenkt ved addisjon fordi de ikke kjenner begrepsbruken • Barn har lett for å svare rutinemessig, som forrige gang, og å utføre oppgaver på samme måte etter hverandre. Derfor bør en ha de vanskeligste oppgavene først. • Skal en lokke fram de beste strategiene må det være oppgaver innenfor deres nærmeste læringssone, ellers førsøker de ikke å tenke. . RA 200109 Innføring i matematikkvansker 3 8

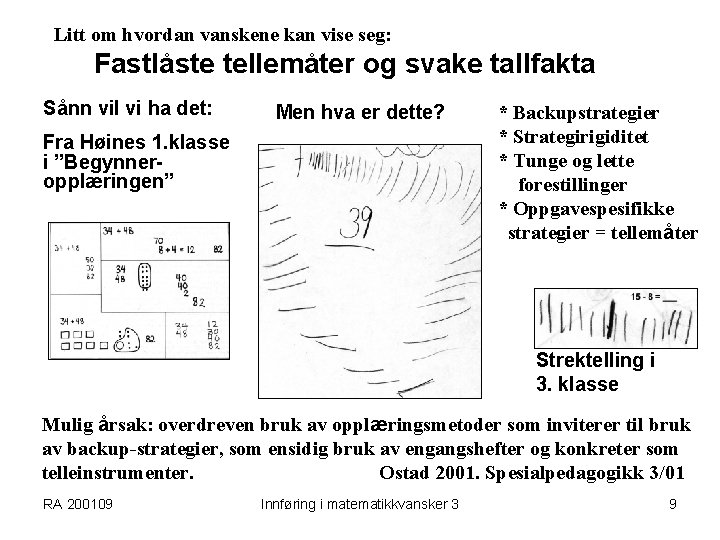
Litt om hvordan vanskene kan vise seg: Fastlåste tellemåter og svake tallfakta Sånn vil vi ha det: Men hva er dette? Fra Høines 1. klasse i ”Begynneropplæringen” * Backupstrategier * Strategirigiditet * Tunge og lette forestillinger * Oppgavespesifikke strategier = tellemåter Strektelling i 3. klasse Mulig årsak: overdreven bruk av opplæringsmetoder som inviterer til bruk av backup-strategier, som ensidig bruk av engangshefter og konkreter som telleinstrumenter. Ostad 2001. Spesialpedagogikk 3/01 RA 200109 Innføring i matematikkvansker 3 9

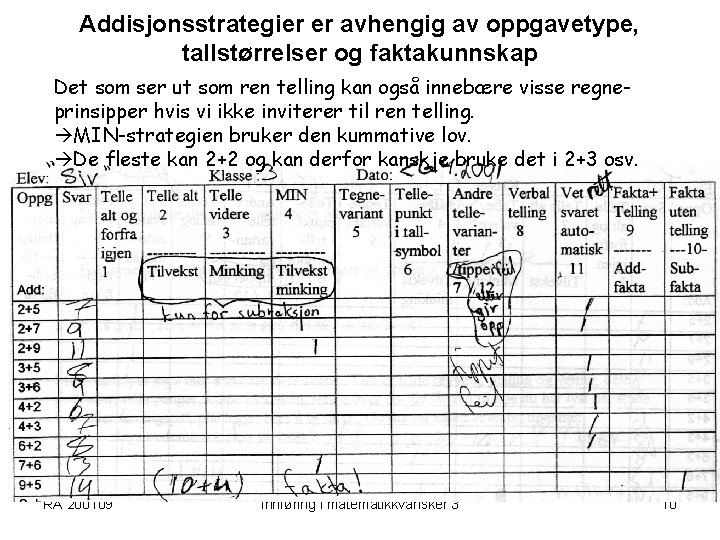
Addisjonsstrategier er avhengig av oppgavetype, tallstørrelser og faktakunnskap Det som ser ut som ren telling kan også innebære visse regneprinsipper hvis vi ikke inviterer til ren telling. MIN-strategien bruker den kummative lov. De fleste kan 2+2 og kan derfor kanskje bruke det i 2+3 osv. RA 200109 Innføring i matematikkvansker 3 10

Dowker: Estimering bygger på tallforståelse (Dowker 2005: 149) Dowker påpeker at bruk av regneprinsipper sparer arbeidshukommelsen, og en kan alltid gi et omttrentelig svar. • Ned til 2 år: har tendens til å anslå for mange baller når du legger til, men for få når du tar bort. • 5 år: mange legger til 1 til en den største addenden • Noen 6 åringer kan anslå omtrentlige summer (8+6 12, 12+13 21) • 8 åringer i tosifrete plusstykker legger gjerne sammen 10 -erne og så enerene mer tilfeldige • En klasse med 10 -åringer som hadde fått undervisning i avrunding brukte konsekvent å runde av begge addende før de plusset. (23+39 20+40 = 60) - andre regnet nøyaktig først og rundet av etterpå. - viktig å påpeke at dette kan ses som uavhengige ferdigheter RA 200109 Innføring i matematikkvansker 3 11

Dowker: avledete faktastrategier (Dowker 2005: 124) • Elever med matematikkvansker er kjent for å bruke rigide tellestrategier, og at årsaken kan være for mye ensidig telling i undervisningen. Dette gjør at de ikke utvikler regnefakta. • MEN: det er ikke undersøkt hvilke tidlige regnefakta som disse elevene kanskje har og hvordan de tar i bruk enkle regnefakta. Seinere blir disse prinsippene viktige for ikke å være helt avhengig av minnelrevende algoritmer, men ved å gjøre gode overslag. • Dowker setter fingeren på dette og peker på fire viktige prinsipper for den tidlige regningen: 1. Oppdeling: 6+8=? , jo 6+6=12 så det må bli to mer, altså 6+8=14 2. Erstatning: 3+6=? , jo 3+7 er jo 10, så da må dette bli en mindre; 9. 3. Regruppering: 21+32=20+30+1+2= 50+3=53 4. Se på forholdet mellom pluss og minus og tenke ”det motsatte”. RA 200109 Innføring i matematikkvansker 3 12

Dowker: avledete faktastrategier (Dowker 2005: 124) Math Recovery: Oppsgaven 32+40 ved hjelp av avledete faktastrategier og tallinja som hjelpemiddel. RA 200109 Innføring i matematikkvansker 3 13

Dowker : De grunnleggende aritmetiske prinsipper 1. Identitetsprinsippet: Hvis du blir fortalt at 8+6=14 så kan du automatisk gi det svaret hvis du blir spurt om det samme rett etter 2. det kommutative prinsipp: 9+4 = 4+9 3. N+1 prinsippet: 23+44=67, da må 23+45 være én mer. 4. N-1 prinsippet 5. Nx 10 prinsippet: 26+72=98, 260+720=980 6. Pluss/minus motsatt-prinsippet: 46+27=73, da må 73 -27 være 46. For å undersøke hvilke prinsipper de kan gir de først en oppgave de kan løse. Så får de en oppgave som er litt vanskeligere. De blir spurt om de kan bruke det forrige svaret til finne svaret på den nye oppgaven. På denne måten lokkes den beste strategien fram. (Dowker 2005, 1998: 282) RA 200109 Innføring i matematikkvansker 3 14

En for ensidig algoritmetrening? La oss prøve et eksempel på hoderegning. Tenk i 10 sekunder på dette regnestykket: » 400 - 278 = Tenkte du pluss eller minus? Vurderte du forskjellige løsningsmåter? RA 200109 Innføring i matematikkvansker 3 15

Terningspill til 100 • Gir øvelse i overslag ved å måtte tenke over om det er lurt å la terningen f. eks. telle 5 eller 50. 10 1 • Hver spiller har et ruteark 7 x 2 • Slå terningen 7 ganger. Hver gang må du velge om tallet skal settes på ener- eller tierplass. • Vinneren er første til 100 Fra: Janne Fauskanger RA 200109 Innføring i matematikkvansker 3 16

De enkleste regnestrategier knyttet til tallstørrelser 1. Nullkombinasjoner: 10+40, 80 -60 2. En-kombinasjon: 382+1, 1+382, 382 -1 3. Doblinger: 2+2, 3+3, 4+4, 7+7 osv. 4. Dobling pluss 1: 12+13 = 12+12+1 5. Tiervenner 6. Ni er nesten 10: Legger til 10 og tar bort en, 16+9 = 16+10 -1 7. Å fylle opp tiern: 16+9 = 16+4+5 = 20+5 8: Naboer: å vite at en til eller en mindre er naboen på tallinja (Alseth 1998: 55) RA 200109 Innføring i matematikkvansker 3 17

Math Recoverys stadier i tidlig regneutvikling ved telling MR 2: De første regneprinsipper med telling (antallforståelse)8: Plussoppgaver ved telling av brikker, skjulte og synlige - 8 b: Plussing med en manglende addend (■■■■ + ? = ■■■■■■) - 9 a: Skriftlige subtraksjonsoppgaver - 9 b: Manglende subtrahend (telle-ned-til) - 9 c: Fjerning av gjenstander (telle-ned-fra) Stadie 0: Haltende telling uten 1 -til-1 korrespondanse Stadie 1: Kan telle opp synlige ting, og å telle de sammen Stadie 2: Kan telle sammen to skjulte mengder, teller alt fra én. Stadie 3: Begynnende tallinjebruker; kan telle videre ved addisjon og telle ned-fra ved minus. Dette tilsvarer nivå MIN-strategi Stadie 4: Trygg tallinjebruker; kan også telle ned-til ved sub. Stadie 5: Avansert tallinjebruker; behersker flere ikke-telle-med -1 strategier som kompensering, regnefakta, legge til ti, kommutativitet, pluss minus er invers, s. 70 (Wright mfl. 2006) RA 200109 Innføring i matematikkvansker 3 18

Alf 5. trinn: Nasjonal prøve 2007 Oppgave som en klare med overslagsregning ”Glemmer” minnetegnet. Bruker han det ellers? Han klarer 70 - (2 x 27), men gjorde sikkert et grovere overslag, eller? Flott! RA 200109 Oppmerksomhetssvikt eller forståelsesproblem? Innføring i matematikkvansker 3 19

Overslag i Alle teller (Alle teller) Alle teller har bare 1 oppgave for overslag på 2. og 3. trinn og ingen på 4. og 5. trinn, så her må en se på andre prøver. • 8. 1 Overslag med små tall (2. 10, 3. 9, samme oppgave) - Omtrent hvor mange ting så du? (vis bilde av 8 og 18 ting i 3 sek) • 8. 2 Overslag opp til 100 (3, 4. 11? (pil på tallinje) • 8. 3 Strategier for overslag (5? , 6, 7, 8, 9, 10) - tenk på en kjent mengde, størrelse eller mål - bruk undergrupper som halvering og gjennomsnitt • 8. 4 Vurdere svar i add- og sub. oppgaver (10) • 8. 5 Vurdere svar i multi- og div. oppgaver (10) RA 200109 Innføring i matematikkvansker 3 20

Kjennetegn 5: Plassverdi, posisjonssystemet Posisjonssystemet tar 4 år å lære? (Lindland 2007) • 10 er ikke bare et nytt tall, men innfører et helt nytt prinsipp; at vi velger å dele inn i tiere. (Men det gjelder ikke for tid!) • Dette forutsetter derfor forståelse av å dele inn mengder i grupper for å ”lette tellinga”. • Fra nå av er lange rekketellinger bare et handicap og må avvennes Ha masse mynter, tiere og kronestykker • Bruk kontekst / PENGER: Ha masse tikroner og kronestykker: Vis verdien av 43 kroner på tre forskjellige måter: - med så få mynter som mulig - med så mange mynter som mulig - med bare tiere RA 200109 Innføring i matematikkvansker 3 21

AT: Plassverdi, posisjonssystemet Kap. 3. 1: Gruppere sammen ting og telle de. Se at en enhet av mange deler også kan ses som én helhet. ( en tier som én enhet) Øv: Del opp 63 på forskj måter, 10 -base materiell 1, 2 & 3. trinn: ingen 4. trinn: 6. Byggverk med 3 og 3 mursteiner. Hvor mange ? (3. 1) Kap. 3. 2: Ener- og tierplass. 3. 3: og hunderplass 1 & 2 trinn: ingen 3. trinn: - 6. Ring rundt det miste tallet (3. 2) - 7. Lag to tall mellom femti og hundre av sifrene 4, 7, 3, 9 - 8: Skya: I tallet ” 14” betyr sifferet 1 __ stjerner. (3. 2) 4. trinn: - 9. Hva kommer rett før seks hundre? (3. 3) - 10. Født i 2007. Når hundre år? (men er det egt. prbl her? Kap. 3. 4: Tallinja. Plassere tall riktig - 11. Hvor på tallinja står pilen (3. 4) Alle teller knytter det ikke til regneferdigheter som Dowker gjør. RA 200109 Innføring i matematikkvansker 3 22

Posisjonssystemet E. Lindland 2007. Kunnskap om posisjonssystemet. I: Tangenten 1/07 Forutsetninger for å forstå posisjonssystemet: • Telling: med én og 10; 4, 14, 24 … (gir oppdelingsferd. ) • Oppdeling av flersifrede tall: 32 er 3 tiere og 2 enere, men også 2 tiere og 12 enere • Gruppering: som å fylle ut tieren ved 8+5 = 8+2+3 • Tallrelasjoner: kjenne tallinjens logikk med større verdi til venstre og mindre til høyre Nivå forståelse av tosifrede heltall: 1. Nivå: Det tosifrede tallet blir sett som en helhet (ingen forståelse) 2. Nivå: Startkunnskap om pos. , vet hva som er enere- og tierplass 3. Nivå: De to sifrene blir sett på som representanter for ulike objekt 4. Nivå: Sifferet på tierplassen representerer grupper av 10 5. Nivå: Tallet viser hele antallet ved hjelp av tiere og enere. Ikke av betydning om materiell er delt opp på en kanonisert- eller ikke-k. måte RA 200109 Innføring i matematikkvansker 3 23

Test av forståelse for posisjonssystemet E. Lindland 2007. Kunnskap om posisjonssystemet. I: Tangenten 1/07 • Oppgave 1: Skriv tallet: 15, 129, 7013, 4006 (gis muntlig) • Oppgave 2: Tallrelasjoner: Tallens gis skriftlig på et ark. - Hvilket av disse to tallene har høyest verdi: 42601 423520 - Hvilket tall kommer rett etter 273999 når vi teller? - Hvilket tall kommer rett før 2450 når vi teller? • Oppgave 3: Oppdeling: Tell opp så mange brikker som tallet på arket viser (16). - Vis med brikkene hva denne delen av tallet står for (6) - Vis med brikkene hva denne delen av tallet står for (1) • Oppgave 4: Vis ark med tallet 43 og 43 firkanter delt i 4 tierkolonner og 3 enere. Intervjueren setter ring rundt sifferet 3 og sier: - Tegn en ring rundt de rutene som viser til denne delen (3) av 43. Intervjueren tegner ring rundt sifferet 4 og sier: - Tegn en ring rundt de rutene som viser til denne delen (4) av 43. (de 4 kolonnene med ti i hver) RA 200109 Innføring i matematikkvansker 3 24

Test av forståelse for posisjonssystemet (2) E. Lindland 2007. Kunnskap om posisjonssystemet. I: Tangenten 1/07 • Vis et annet ark med 43 ruter, men nå organisert i 3 tierstaver og 13 enkle ruter. -Tegn ring rundt de rutene som viser til denne delen (3) av 43. - Tegn ring rundt de rutene som viser til denne delen (4) i 43. • Oppgave 5: Vis ark med tallet 26 og 26 stjerner som er gruppert i 6 grupper av 4 og en gruppe av 2. Tegner en ring rundt sifferet 6 og sier: - Tegn en ring rundt de stjernene som viser til denne delen av (6) av 26. - Tegn en ring rundt de stjernene som viser til denne delen av (2) av 26. • Oppgave 6: Ser på ark med tallet 37. - Hvilket tall står her? - Hvilket tallsiffer står på enerplassen? - Hvilket tallsiffer står på tierplassen? • Så tilsvarende med 415. RA 200109 Innføring i matematikkvansker 3 25

Konkretisering av posisjonssystemet Magne 1986: 198. Långsamt blev Johan förtrogen med materialet och mot slutet i andra årskursen klarade Johan att lägga rätt bitar när han ville tänka t. ex. på talet 207. Länge kunde Johan bara klara tal om han hade centimo till hands, men en dag hånde något. Johan skrev ned ett tal och visade det för fröken utan att använda materialet. Det gick lika bra dagen efter och då sade han triumferande till läraren: "Jag behöver inte klossarna för när jag skriver 207 har jag två plattor och sju enbitar i huvet och inga stavar alls. Så du förstår fröken, att då är det 207. " Detta år ett exempel bland många på att låra sig visualisering av flersiffriga tal. RA 200109 Innføring i matematikkvansker 3 26

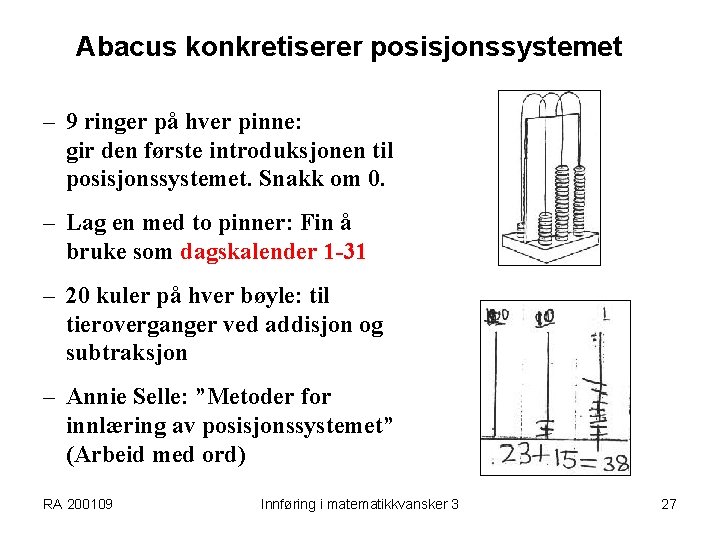
Abacus konkretiserer posisjonssystemet – 9 ringer på hver pinne: gir den første introduksjonen til posisjonssystemet. Snakk om 0. – Lag en med to pinner: Fin å bruke som dagskalender 1 -31 – 20 kuler på hver bøyle: til tieroverganger ved addisjon og subtraksjon – Annie Selle: ”Metoder for innlæring av posisjonssystemet” (Arbeid med ord) RA 200109 Innføring i matematikkvansker 3 27

Tegn 6: Utviklingen av tabeller, regnefakta Manglende automatisering av de vanligste tallkombinasjoner er kanskje det mest vanlige tegnet ved matematikkvansker. Årsaker: Minnet, for mye telling, men også lite fokus på plussing. Fra ung. skolen meldes det gjerne om svake gangeferdigheter, men hva med pluss? • Gutt, 8. trinn: ”Regn så mange som mulig på 2 minutter”. • Karamellstykket 8 x 7 RA 200109 Innføring i matematikkvansker 3 28

Testing av regnefakta Vi mangler normering av utviklingen av tabellferdigheter selv om dette regnes som et av de aller tydeligste tegn på matematikkvansker. Denne testen er ”privat” normert med 100 5 -klassinger i en kommune. Regn så mange du kan på 2 min. ! Alf, 5. trinn: Prøve tatt med noen måneders mellomrom. To forskjellige strategier!!!, men 11 rette begge ganger (1 under kritisk grense). Når individuelt så kan en etterpå få vite hva han måtte telle og hvilke fakta han brukte. RA 200109 Innføring i matematikkvansker 3 29

Tren 10 -venner med kabal Kabal: Du kan ta bort kort som til sammen blir 10 og som ikke er skjult av andre kort. (Bildekortene er tatt bort) Enklere: Bruk bare kort opp til 5 og legg opp tre rader. Drill til slutt: Legg kortene som er 10 -venner under hverandre, se mønsteret, si de høyt, ta vekk kortene og gjenta høyt flere ganger ”tre pluss syv er ti osv. RA 200109 Innføring i matematikkvansker 3 30

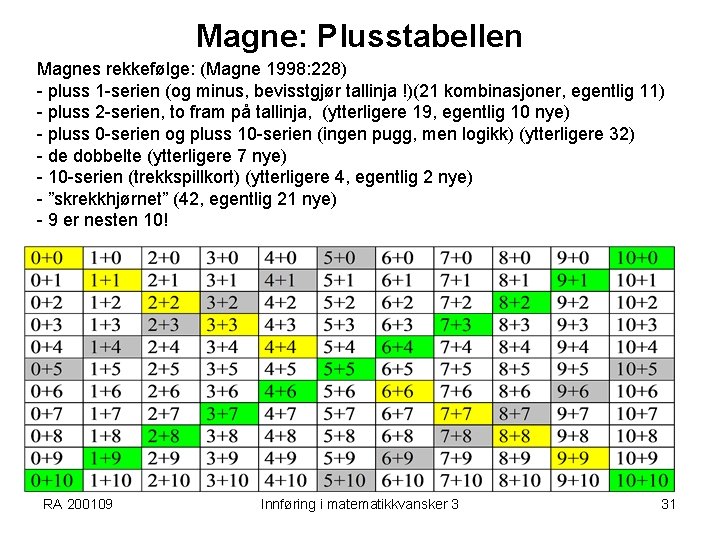
Magne: Plusstabellen Magnes rekkefølge: (Magne 1998: 228) - pluss 1 -serien (og minus, bevisstgjør tallinja !)(21 kombinasjoner, egentlig 11) - pluss 2 -serien, to fram på tallinja, (ytterligere 19, egentlig 10 nye) - pluss 0 -serien og pluss 10 -serien (ingen pugg, men logikk) (ytterligere 32) - de dobbelte (ytterligere 7 nye) - 10 -serien (trekkspillkort) (ytterligere 4, egentlig 2 nye) - ”skrekkhjørnet” (42, egentlig 21 nye) - 9 er nesten 10! RA 200109 Innføring i matematikkvansker 3 31