It Aint Over Till Its Over Playoff Races

It Ain’t Over Till It’s Over: Playoff Races and Optimization Modeling Exercises Eli Olinick Engineering Management, Information, and Systems 1

Motivating Question: Can The Giants Win the Pennant? National League West September 8, 1996 Games Team Wins Losses Back Left Dodgers 78 63 21 Padres 78 65 1. 0 19 Rockies 71 71 7. 5 20 Giants 59 81 18. 5 22 According to traditional statistics, the Giants are not “mathematically” It ain’t over Department Eliminated (59+22= 81 Engineering > 78). Management, Information, and Systems till it’s over 2

But What About the Schedule? Games Team Wins Losses Back Left Dodgers 78 63 21 Padres 78 65 1. 0 19 Rockies 71 71 7. 5 20 Giants 59 81 18. 5 22 It ain’t over till it’s over … unless it’s over • The Dodgers and Padres will play each other 7 more times • There are no ties in baseball • One of these two teams will finish the season with at least 82 wins • Since they can finish with at most 81 wins, the Giants have Engineering Management, Information, and Systems Department already been eliminated from first place 3

Selling Sports Fans on the Science of Better • The traditional definition of “mathematical elimination” is based on sufficient, but not necessary conditions (Schwartz [1966]) • Giants’ elimination reported in SF Chron. until 9/10/96, but Berkeley RIOT website (http: //riot. ieor. berkeley. edu/~baseball) reported it on 9/8/96 [Adler et al. 2002] • OR model shows elimination an average of 3 days earlier than traditional methods in 1987 MLB season (Robinson [1991]) – In some sports the traditional calculations are based on methods aren’t even sufficient! • Soccer clinches announced prematurely (Ribeiro and Urrutia [2004]) • A simple max-flow calculation can correctly determine when a team is really “mathematically eliminated” • More interesting questions can be answered by solving Engineering Management, Information, and Systems Department straight-forward extensions to the max-flow model 4

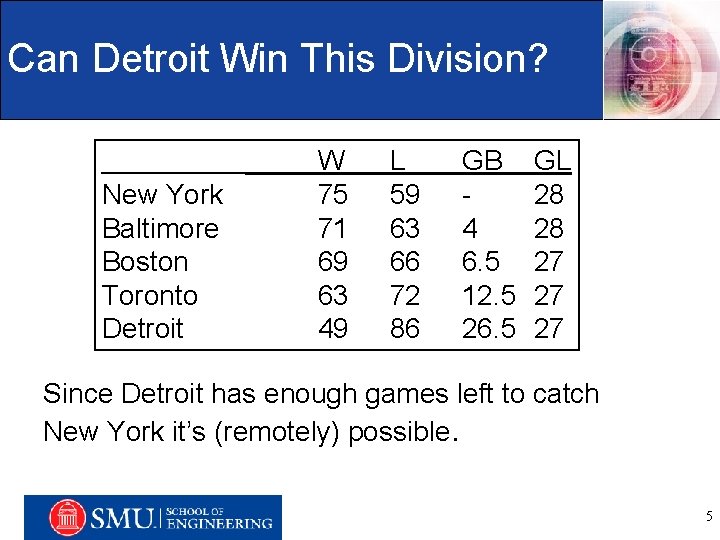
Can Detroit Win This Division? New York Baltimore Boston Toronto Detroit W 75 71 69 63 49 L 59 63 66 72 86 GB 4 6. 5 12. 5 26. 5 GL 28 28 27 27 27 Since Detroit has enough games left to catch New York it’s (remotely) possible. Engineering Management, Information, and Systems Department 5

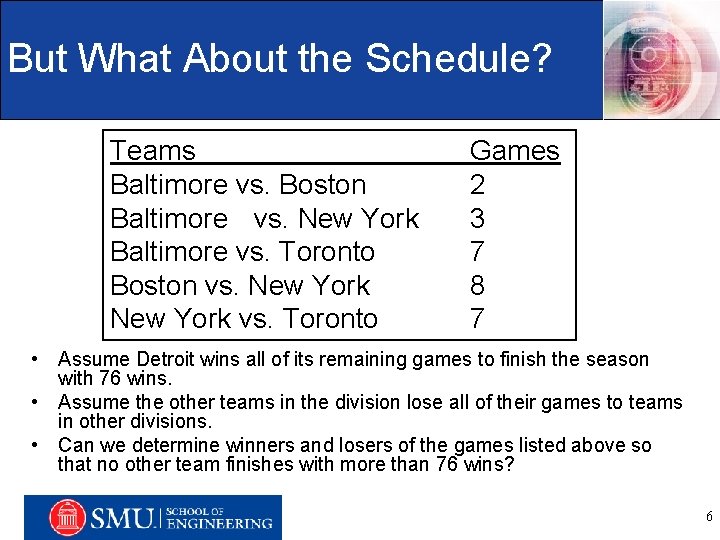
But What About the Schedule? Teams Baltimore vs. Boston Baltimore vs. New York Baltimore vs. Toronto Boston vs. New York vs. Toronto Games 2 3 7 8 7 • Assume Detroit wins all of its remaining games to finish the season with 76 wins. • Assume the other teams in the division lose all of their games to teams in other divisions. • Can we determine winners and. Management, losers of the gamesand listed above so Engineering Information, Systems Department that no other team finishes with more than 76 wins? 6

Proof of Detroit’s Elimination • Laborious analysis of possible scenarios – If New York wins two or more games, they will finish with at least 77 wins. Detroit is out. – If New York loses all of their remaining games, then Boston will win at least 8 more games which would give them at least 77 wins. Detroit is out. – If New York wins exactly 1 more game … Detroit is out. Engineering Management, Information, and Systems Department 7

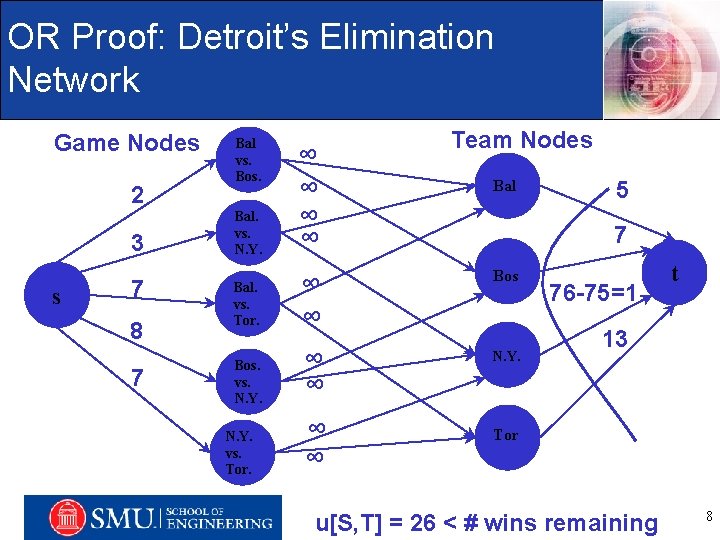
OR Proof: Detroit’s Elimination Network Game Nodes 2 3 s 7 8 7 Bal vs. Bos. Bal. vs. N. Y. Bal. vs. Tor. Bos. vs. N. Y. ∞ ∞ ∞ ∞ Team Nodes Bal 5 7 Bos N. Y. 76 -75=1 t 13 ∞ ∞ Tor N. Y. vs. Engineering Management, Information, and Systems Department Tor. u[S, T] = 26 < # wins remaining 8

RIOT Site September 8, 2004 Engineering Management, Information, and Systems Department 9

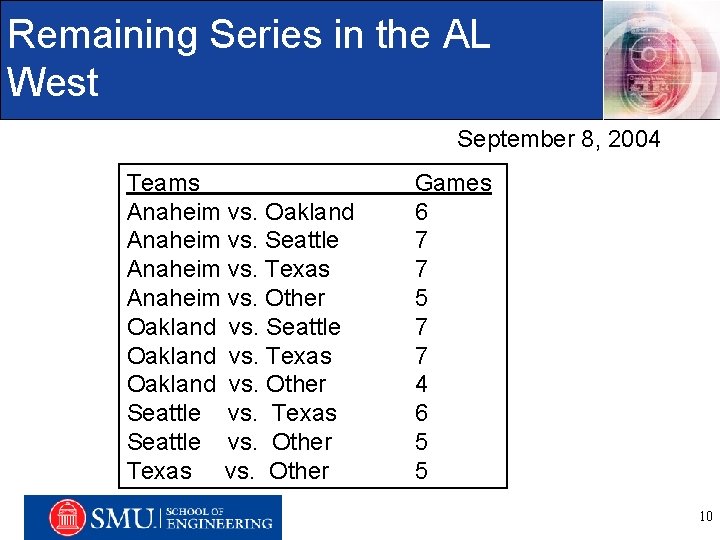
Remaining Series in the AL West September 8, 2004 Teams Games Anaheim vs. Oakland 6 Anaheim vs. Seattle 7 Anaheim vs. Texas 7 Anaheim vs. Other 5 Oakland vs. Seattle 7 Oakland vs. Texas 7 Oakland vs. Other 4 Seattle vs. Texas 6 Seattle vs. Engineering Other. Management, 5 Information, and Systems Department Texas vs. Other 5 10

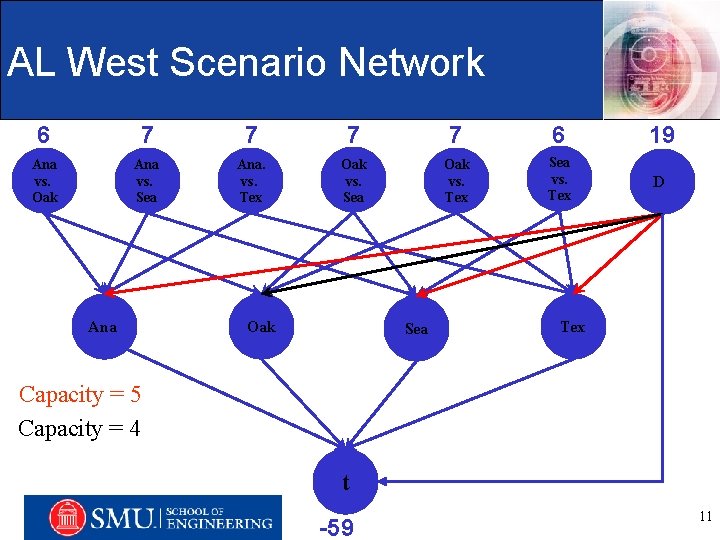
AL West Scenario Network 6 7 7 6 19 Ana vs. Oak Ana vs. Sea Ana. vs. Tex Oak vs. Sea Oak vs. Tex Sea vs. Tex D Ana Oak Sea Tex Capacity = 5 Capacity = 4 Engineering Management, Information, and Systems Department t -59 11

How close is Texas to elimination from first place? • Find an end-of-season scenario where Texas wins the division with a minimum number of additional wins • Texas cannot win the division with fewer additional wins • This is the first place Engineering Management, Information, and Systems Department elimination number 12

How close is Texas to clinching first place? • Find an end-of-season scenario where Texas wins as many games as possible without winning the division (i. e. , at least one other team in the division has a better record) • If Texas wins one more game than the optimal value for w. Tex, then they are guaranteed at least a tie for first place • This is the first-place clinch number Engineering Management, Information, and Systems Department 13

What is an appropriate value for M? • In this particular case: o o o wtex 100 w. Oak 81 w. Ana 79 wsea 51 So, M = (100 -51)+1 = 50 is large enough. • Since each team plays 162 games, M = 162 + 1 = 163 will always work at any point in the Engineering Management, Information, and Systems Department season. 14

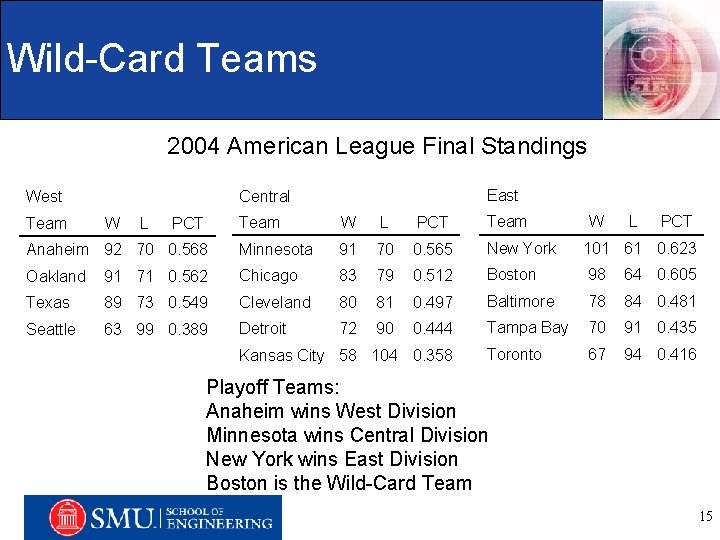
Wild-Card Teams 2004 American League Final Standings East Central West Team W L PCT Team Anaheim 92 70 0. 568 Minnesota 91 70 0. 565 New York 101 61 0. 623 Oakland 91 71 0. 562 Chicago 83 79 0. 512 Boston 98 64 0. 605 Texas 89 73 0. 549 Cleveland 80 81 0. 497 Baltimore 78 84 0. 481 Seattle 63 99 0. 389 Detroit 72 90 0. 444 Tampa Bay 70 91 0. 435 Toronto 67 94 0. 416 Team W L PCT Kansas City 58 104 0. 358 W L PCT Playoff Teams: Anaheim wins West Division Minnesota wins Central Division Engineering Management, Information, and Systems Department New York wins East Division Boston is the Wild-Card Team 15

Formulation Challenges • Elimination and clinch numbers for the Major League Baseball playoffs • Formulations for the NBA playoffs – Playoff structure similar to MLB, but with 5 wild -card teams in each conference – Fans interested in questions about clinching home-court advantage in the playoffs Engineering Management, Information, and Systems Department 16

Formulation Challenges • Futbol – Standings points determined by the 3 -1 system • gij = wij + wji + tij • SPi = 3 wij + tij – Fut. Max project: http: //futmax. inf. puc-rio. br/ • Top 8 teams (out of 26) make the playoffs • Bottom 4 teams demoted to a lower division – Teams wish to avoid elimination from 22 nd place • Playoff/Demotion Elimination/Clinch numbers • NFL – Standings determined by win-lose-tie percentage: SPi = wij + ½ tij – Complex rules for breaking ties in the final standings • NHL – Standings points determined by a 2 -1 -1 system (wins-ties-overtime losses) – Home-ice advantage Engineering Management, Information, and Systems Department 17

References/Advanced Topics • • Battista, M. 1993. “Mathematics in Baseball”. Mathematics Teacher. 86: 4. 336342. LP and Integer Programming – Robinson, L. 1991. “Baseball playoff eliminations: An application of linear programming”. OR Letters. 10(2) 67 -74. – Alder, I. , D. Hochbaum, A. Erera, E. Olinick. 2002, “Baseball, Optimization, and the World Wide Web”. Interfaces. 32(2), 12 -22. – Ribeiro, C. and S. Urrutia. 2004. “OR on the Ball”. OR/MS Today. 31: 3. 50 -54. • Network Flows – Schwartz, B. 1966. “Possible winners in partially completed tournaments”. SIAM Rev. 8(3) 302 -308. – Gusfield, D. , C. Martel, D. Fernandez-Baca. 1987. “Fast algorithms for bipartite maximum flow”. SIAM J. Comp. 16(2) 237 -251. – Gusfield, D. , C. Martel, D. 1992. “A fast algorithm for the generalized parametric minimum cut problem and applications”. Algorithmica. 7(5 -6) 499 -519. – Wayne, K. 2001. “A new property and faster algorithm for baseball elimination”. SIAM J. Disc. Math. 14(2) 223 -229. Engineering Management, Information, and Systems Department 18

RIOT Site September 8, 2004 Engineering Management, Information, and Systems Department 19

References/Advanced Topics • Complexity Results – Hoffman, A. , T. Rivlin. 1970. “When is a team ‘mathematically eliminated’? ”. Proc. Princeton Sympos. On Mat. Programming. – Mc. Cormick, S. “Fast algorithms for parametric scheduling come from extensions to parametric maximum flow. ” Operations Research. 47(5) 744 -756 – Gusfield D. , and C. Martel. 2002. “The Structure and Complexity of Sports Elimination Numbers”. Algorithmica. 32(1) 73 -86. Engineering Management, Information, and Systems Department 20

The “Magic Number” • Definition: the smallest number such that any combination of wins by the first-place team and losses by the secondplace team totaling the magic number guarantees that the first-place team will win the division. – – – Let w 1 = number games the first place team has already won Let w 2 = number games the first place team has already won Let g 2= number games the second place team has left to place The magic number is w 2 + g 2 – w 1 + 1 Derivation exercises in Battista [1993] • Only given for the first-place team with respect to the second-place team Engineering Management, Information, and Systems Department • What about teams that aren’t in first place? 21