ISMERETALAP TECHNOLGIA Elad Kovcs Zita 20162017 II flv

ISMERETALAPÚ TECHNOLÓGIA Előadó: Kovács Zita 2016/2017. II. félév Az osztályozás fogalmának háló alapú bevezetése

Tartalom 1. 2. 3. 4. 5. Bevezetés Hálóelméleti alapfogalmak Fogalmi hierarchia Az osztályozási eljárás Összegzés

1. Bevezetés �osztályozás: az objektumok közötti és az objektumok és tulajdonságaik közötti relációk felépítése �homogén egységeket alakítunk ki

Bevezetés �az osztályozáson alapuló rendszerek különböző útvonalakon alakultak ki: logika szemantikus hálók és keretek osztályalapú nyelvek leíró logikák

Bevezetés �az osztályozáson alapuló rendszerek osztályhierarchián alapulnak �egyedeire az osztályozáson alapuló következtetőrendszerek hatnak �osztályok osztályozása olyan folyamat, melynek során az osztályokat hierarchiába szervezzük vagy a meglévő hierarchiába új osztályt illesztünk

Bevezetés �egyedek osztályozása olyan folyamat, melynek során felismerjük az egyedhez tartozó osztályt �mai előadás célja: megmutasson egy lehetséges megközelítési módot az osztályozás fogalmának bevezetésére a háló algebrai struktúrák segítségével

2. Hálóelméleti alapfogalmak �Legyen S tetszőleges halmaz. �Az R relációt reflexívnek nevezzük, ha minden S-beli a elemre R(a, a). �Az R relációt antiszimmetrikusnak nevezzük, ha minden S-beli a és b elemre, ha R(a, b) és R(b, a), akkor a és b azonosak.

Hálóelméleti alapfogalmak �Az R relációt tranzitívnak nevezzük, ha minden S-beli a, b, c elemre ha R(a, b) és R(b, c), akkor R(a, c). �Az S halmazt részben rendezettnek nevezzük, ha az S bizonyos elempárjaira értelmezve van egy reflexív, antiszimmetrikus és tranzitív R reláció.

Hálóelméleti alapfogalmak �Az S részben rendezett halmazban ∀ a, b ∈ S esetén: R(a, b) vagy R(b, a) vagy a és b nem összehasonlíthatóak. �Legyen S részben rendezett halmaz. S-t (teljesen) rendezettnek nevezzük, ha ∀ a, b ∈ S összehasonlítható.

Hálóelméleti alapfogalmak �Legyen S részben rendezett és a, b, c, x ∈ S. �Az x elemet az a és b elemek felső korlátjának nevezzük, ha R(a, x) és R(b, x). �Az x elemet az a és b elemek alsó korlátjának nevezzük, ha R(x, a) és R(x, b).

Hálóelméleti alapfogalmak �A c elemet az a és b elemek legkisebb felső korlátjának nevezzük, ha c az a és b elemek felső korlátja és ∀ x ∈ S esetén, ha x felső korlátja az a és b elemeknek, akkor R(c, x).

Hálóelméleti alapfogalmak �A c elemet az a és b elemek legnagyobb alsó korlátjának nevezzük, ha c az a és b elemek alsó korlátja és ∀ x ∈ S esetén, ha x alsó korlátja az a és b elemeknek, akkor R(x, c).

Hálóelméleti alapfogalmak �Ha az a és b elemeknek létezik legkisebb felső (legnagyobb alsó) korlátja, egyértelműen meghatározott. �A legkisebb felső korlát: a ∪ b �A legnagyobb alsó korlát: a ∩ b akkor az

Háló fogalma Legyen S részben rendezett halmaz az R relációval. Az {S, R} párost hálónak nevezzük, ha bármely x, y ∈ S elempár esetén létezik legkisebb felső és legnagyobb alsó korlát. �A hálók jelölésekor szokásosan nem említjük az R relációt.

Háló fogalma �Legyen P háló és e, O ∈ P. �Aze elemet egységelemnek nevezzük, ha ∀a∈P esetén R(a, e). �Az O elemet zéruselemnek nevezzük, ha ∀a∈P esetén R(O, a). �Egy hálóban nem feltétlenül létezik egységelem és zéruselem.

Példa hálóra �Az X halmaz összes részhalmaza a halmazelméleti részhalmaza relációval (jelölésben P(X)). �Legyen S teljesen rendezett halmaz. Ekkor S háló, mégpedig � a ∪ b = max(a, b) és a ∩ b = min(a, b).

Példa hálóra �Legyen S a pozitív egészek halmaza, hozzávéve a nullát. Jelentse az R(a, b) reláció azt, hogy a osztója b-nek. Ekkor a ∪ b az a és b legkisebb közös többszöröse és a ∩ b az a és b legnagyobb közös osztója. A háló nulleleme az 1, és egységeleme a nulla.

Példa hálóra �Legyen S a háromdimenziós tér lineáris alakzatainak halmaza (üres halmaz, pontok, egyenesek, síkok és az egész tér). R(a, b) jelentse azt, hogy a benne van b-ben. Ekkor az a ∪ b az a és b alakzatokat tartalmazó legkisebb lineáris alakzat, a ∩ b pedig az a és b alakzatok közös része.

Példa hálóra �Tekintsük a következő számokat: 4, 5, 6, 7, 8 és legyen R a szokásos ≤, azaz R(a, b) jelentése, hogy a ≤ b. 8 7 6 5 4

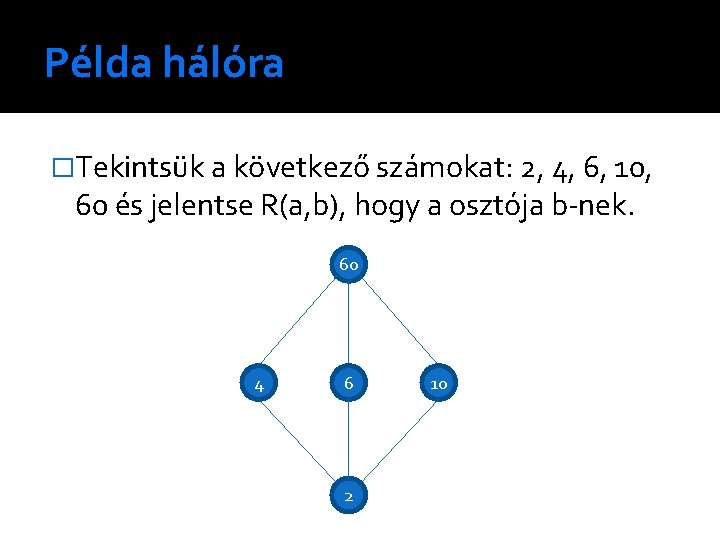
Példa hálóra �Tekintsük a következő számokat: 2, 4, 6, 10, 60 és jelentse R(a, b), hogy a osztója b-nek. 60 4 6 2 10

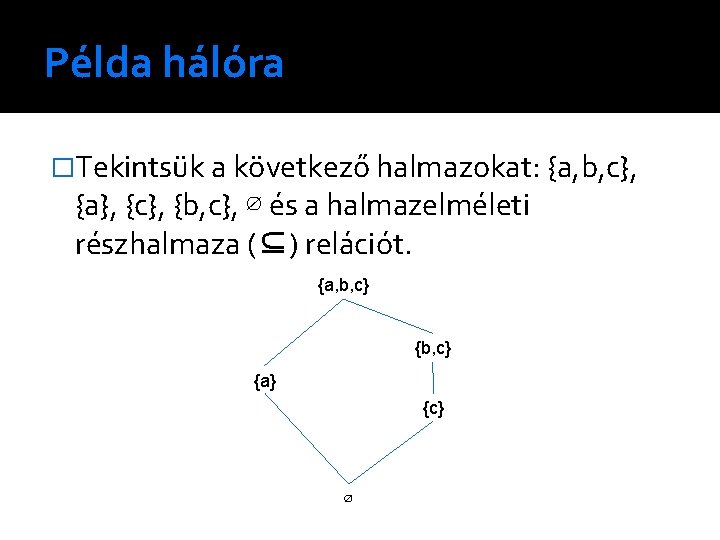
Példa hálóra �Tekintsük a következő halmazokat: {a, b, c}, {a}, {c}, {b, c}, ∅ és a halmazelméleti részhalmaza (⊆) relációt. {a, b, c} {a} {c} ∅

Példa hálóra �Tekintsük a következő intervallumokat: A = [5, 6], B = [4, 7], C = [2, 8], D = [3, 9], E = [1, 10] és R(a, b) jelentse, hogy az a intervallum része a b intervallumnak. E D C B A

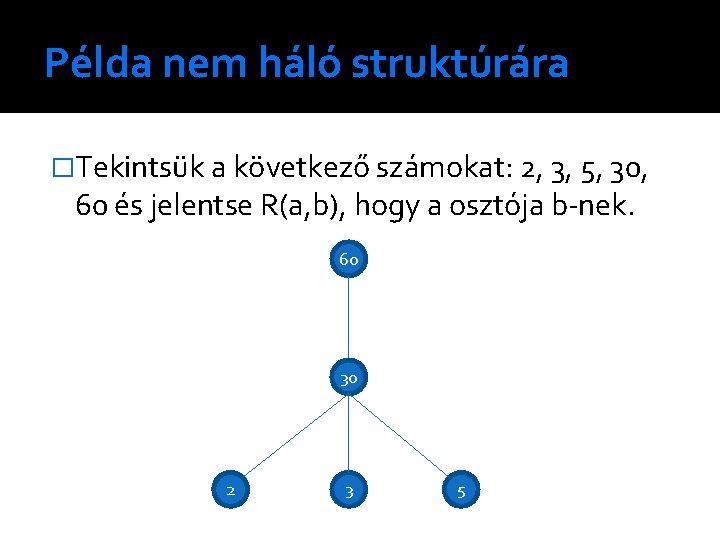
Példa nem háló struktúrára �Tekintsük a következő számokat: 2, 3, 5, 30, 60 és jelentse R(a, b), hogy a osztója b-nek. 60 30 2 3 5

Példa nem háló struktúrára �Tekintsük a következő intervallumokat: A = [4, 5], B = [6, 7], C = [2, 8], D = [3, 9], E = [1, 10] és R(a, b) jelentse, hogy az a intervallum része a b intervallumnak. E C D A B

A hálók tulajdonságai �Legyen P háló, R a P-n definiált részben rendezési reláció és a, b, c ∈ P. �Ha R(a, b), akkor létezik a-nak és b-nek legkisebb felső és legnagyobb alsó korlátja a ∪ b = b és a ∩ b = a.

A hálók tulajdonságai A P hálóban a legkisebb felső és legnagyobb alsó korlátok a következő tulajdonságokkal rendelkeznek: a∪a=a a∪b=b∪a a ∪(b ∪ c) = (a ∪ b)∪ c idempotencia a∩a=a kommutativitás a∩b=b∩a a ∩(b ∩ c) = (a ∩ b)∩ c asszociativitás (a ∪ b)∩ a = a (a ∩ b)∪ a = a elnyelési tulajdonság

A hálók tulajdonságai Legyen az S nemüres halmazban két operáció értelmezve a ∪ b és a ∩ b; az S tetszőleges a, b elemeire úgy, hogy az előbbi 4 feltétel teljesül. Ekkor S háló, amelyben az a, b elemek legkisebb felső korlátja a ∪ b, legnagyobb alsó korlátja a ∩ b. Az R reláció: R(a, b) pontosan akkor, ha a ∩ b = a.

A hálók tulajdonságai �Az 1 -4 tulajdonságokat gyakran háló axiómáknak is nevezzük.

A hálók tulajdonságai Ha a P háló véges halmaz, akkor van egységeleme és zéruseleme. �Legyen P = {a 1, a 2, . . . , an}. �Akkor e = a 1 ∪ a 2 ∪. . . ∪ an �és O = a 1 ∩ a 2 ∩. . . ∩ an. �Ha az egységelem és a zéruselem léteznek, akkor egyértelműen meghatározottak.

Az egységelem és a zéruselem tulajdonságai az S tetszőleges a elemére 1. e ∪ a = e e∩a=a 2. O ∪ a = a O ∩ a = O

Az egységelem és a zéruselem tulajdonságai Legyen S rendezett halmaz. �Akkor S háló, amelyben a ∪ b = max(a, b) és a ∩ b = min(a, b).

Moduláris hálók Tétel: Tetszőleges hálóban R(x, z) ⇒ R(x ∪(y ∩ z), (x ∪ y)∩ z) Bizonyítás: Mivel R(x, x ∪ y) és R(y ∩ z, y) és R(y, x ∪ y) és a tranzitivitás miatt R(y ∩ z, x ∪ y) ezért R(x ∪(y ∩ z), x ∪ y) valamint R(x, z) és R(y ∩ z, z) -ből következik, hogy R(x ∪(y ∩ z), z) és így R(x ∪(y ∩ z), (x ∪ y)∩ z)

Moduláris hálók Definíció: Az olyan hálót, amelyben R(x, z) ⇒ x ∪(y ∩ z) = (x ∪ y)∩ z moduláris hálónak nevezzük.

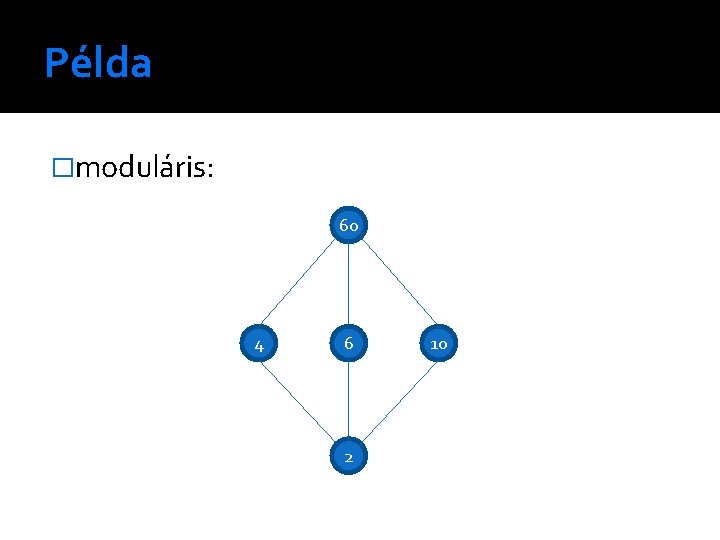
Példa �moduláris: 60 4 6 2 10

Disztributív hálók Tétel: Tetszőleges hálóban R(x ∪(y ∩ z), (x ∪ y)∩(x ∪ z)) R((x ∩ y)∪(x ∩ z), (x ∩(y ∪ z)). Tétel: Egy hálóban az 1. azonosság pontosan akkor teljesül, ha a 2. azonosság is teljesül. 1. x ∪(y ∩ z) = (x ∪ y)∩(x ∪ z) 2. x ∩(y ∪ z) = (x ∩ y)∪(x ∩ z)

Disztributív hálók Definíció: Egy hálót amelyben az 1. azonosság (következésképpen a 2. azonosság) teljesül, disztributív hálónak nevezü nk.

Példa �Egy halmaz összes részhalmazainak halmaza disztributív háló (∩ és ∪ a szokásos halmazelméletei műveletek). �Egy teljesen rendezett halmaz disztributív háló (∩, a legnagyobb alsó korlát az elemek minimuma, ∪, a legkisebb felső korlát az elemek maximuma).

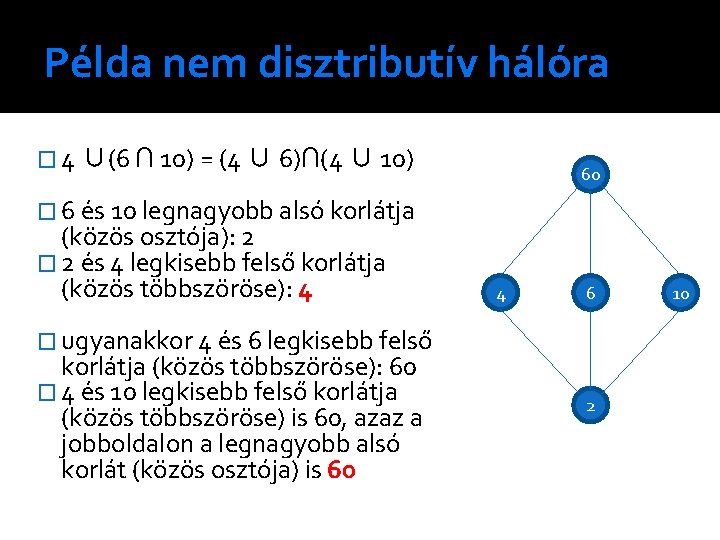
Példa nem disztributív hálóra � 4 ∪(6 ∩ 10) = (4 ∪ 6)∩(4 ∪ 10) 60 � 6 és 10 legnagyobb alsó korlátja (közös osztója): 2 � 2 és 4 legkisebb felső korlátja (közös többszöröse): 4 4 6 � ugyanakkor 4 és 6 legkisebb felső korlátja (közös többszöröse): 60 � 4 és 10 legkisebb felső korlátja (közös többszöröse) is 60, azaz a jobboldalon a legnagyobb alsó korlát (közös osztója) is 60 2 10

Boole algebra �Legyen L háló, amelynek egységeleme e és nulleleme 0. �Az a ∈ L elem komplemensének nevezzük azt az a L-beli elemet, amelyre a ∪ a =e és a ∩ a = O. �Nyilvánvaló, hogy a komplemense éppen a. �O és e egymás komplemensei.

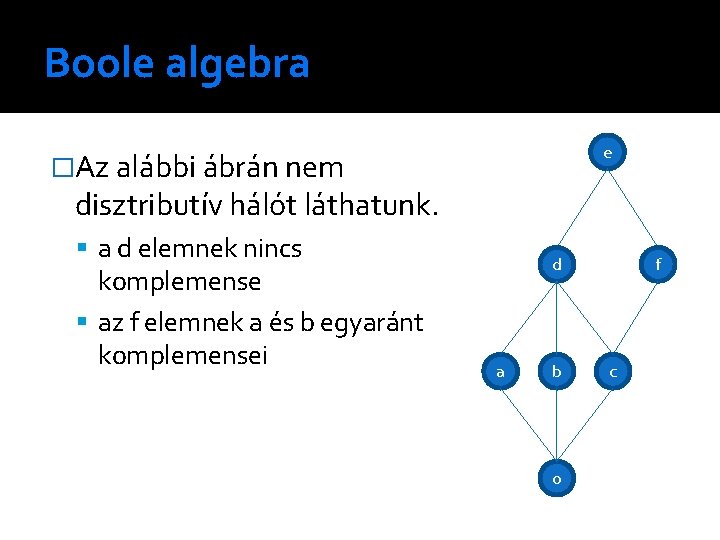
Boole algebra e �Az alábbi ábrán nem disztributív hálót láthatunk. a d elemnek nincs komplemense az f elemnek a és b egyaránt komplemensei d a b o f c

Boole algebra Tétel: Egy L disztributív háló minden elemének legfeljebb egy komplemense lehet. Az előbbi ábrából a b elemet és a o-d élet törölve disztributív hálót kapunk, amelyben a d-nek továbbra sincs komplemense.

Boole algebra Definíció: Egy olyan disztributív hálót, amelyben minden elemnek van komplemense Boole-féle algebrának nevezünk.

Boole algebra Tétel: Ha a, b B boole-algebrai elemek, akkor (a ∪ b) = a ∩ b és (a ∩ b) = a ∪ b

3. Fogalmi hierarchia �a valós világ egy fogalmát reprezentáló osztály egy generikus egység, amely csoportosít egy elemhalmazt és amely egy saját leíróval rendelkezik. �tehát egy C osztályhoz tartozik egy rá jellemző, a reprezentált fogalom állapotát és viselkedését leíró tulajdonsághalmaz

Fogalmi hierarchia A C osztály konjunkciókkal is kifejezhető, C = (a 1, s 1) ⊓ (a 2, s 2). . . , ⊓ (an, sn) ahol � az ak attribútum és � sk az attribútumhoz kapcsolódó specifikáció, � pontosítva az értékek típusát, a tartományát és számosságát (ak-k páronként különbözőek).

Fogalmi hierarchia �az osztályok klasszifikációja során: az osztályhoz tartozó egyedek közös tulajdonságait csoportosítjuk

Fogalmi hierarchia �az alárendelés egy általános reláció, amely az osztályok hierarchiába szervezését biztosítja (pontos definíció: lásd leíró logikáknál) �egy C osztály alárendeli egy D osztály (C⊑D), ha D minden attribútuma C-ben is megtalálható a C attribútumai mutatják a D attribútumainak állapot specifikációját

Fogalmi hierarchia Definíció: Egy H fogalmi hierarchia egy (χ, ⊤, ⊑) háló, ahol � χ osztályok véges halmaza, � ⊑ az osztályokon definiált részben rendezési reláció, amit alárendelésnek nevezünk, és � ⊤ a χ egységeleme a ⊑ relációra nézve. ⊤-t a hierarchia gyökerének nevezzük.

Fogalmi hierarchia �A χ háló diagramjában a D→C él jelöli azt a tényt, hogy a C osztály alárendeli a D osztályt.

Az osztályozási eljárás �a H-beli objektumok között megtalálható implicit függőségekre világít rá osztály-osztály osztály-egyed �lehetővé teszi, hogy felismerjünk egy objektumot a hierarchiára vonatkozó tulajdonságait azonosítva

Az osztályozási eljárás A klasszifikáció egy hozzátartozási döntési eljárás. Egy x objektum elhelyezése a H hierarchiába a következőképpen sematizálható: (χ, ⊤, ⊑) × {x} → (χ ∪ {x}, ⊤, ⊑) A klasszifikáció az osztály állapotát jellemző tulajdonságok szükséges és elegendő jellegén alapul.

Az osztályozási eljárás �Szükséges feltétel: Legyen C egy osztály és i a C osztály egyede. Ekkor i a C osztály minden attribútumával rendelkezik. �Elegendő feltétel: Legyen x olyan objektum, amely C minden tulajdonságával rendelkezik. Ebben az esetben x osztályozható úgy, mint a C osztály egyede.

Egy klasszifikációs algoritmus Az a klasszifikációs művelet, amely lehetővé teszi, hogy az x objektumot elhelyezzük a H hierarchiába három lépésre bontható: 1. az x legspecifikusabb alárendelőinek (SA) keresése 2. az x legáltalánosabb alárendeltjeinek (AA) keresése 3. az x objektum és az alárendeltjei, valamint az alárendelői közötti új relációk kialakítása

A legspecifikusabb alárendelők keresése Az alapötletet az adja, hogy járjuk be mélységi bejárással az osztályok gráfját mindaddig, amíg olyan osztályt nem találunk, amely nem felel meg az osztályozandó objektum tulajdonságainak.

A legáltalánosabb alárendeltek keresése � Elegendő csak azon SA-k utódait vizsgálni, amelyek ugyanazon tulajdonságokkal rendelkeznek, mint az osztályozandó objektum. � Ha ez az objektum alárendel egy utódot, akkor ez egy SA és az ő utódait figyelmen kívül hagyjuk, különben az utódokat sorra teszteljük, amikor a bejáráskor hozzájuk érünk.

A legáltalánosabb alárendeltek keresése � a legáltalánosabb alárendelt nem feltétlenül közvetlen alárendeltje a legspecifikusabb alárendelőnek

Az x objektum és az alárendeltjei, valamint az alárendelői közötti új relációk kialakítása �amikor az x objektumnak megfelelő SA-it és AA-it megtaláltuk, akkor kialakítjuk az új kapcsolatokat az x objektumnak megfelelő osztály, valamint az SA-k és AA-k között �ellenőrizzük, hogy ez az új osztály már jelen van-e a hierarchiában

Algoritmus Legyen �X a hierarchiában elhelyezendő objektum és �Objektum a hierarchia gráf gyökere. Ekkor mélységi kereséssel a HASONLIT eljárás szolgáltatja az X legspecifikusabb alárendelőit.

HASONLIT(Objektum, X) HA X nem alárendeltje Objektumnak AKKOR (a hierarchiában Objektum egyetlen utódja sem rendeli alá Xet) RETURN nil EGYÉBKÉNT (Objektum ideiglenesen a legspecifikusabb alárendelő) HA Objektum levélelem AKKOR RETURN Objektum EGYÉBKÉNT SA lokális változó SA=nil Objektum minden UTOD utódjára DO SA=SA ∪ HASONLIT(UTOD, X) (Ha SA nem nil, akkor az Objektum egyik utódja a legspecifikusabb alárendelő) HA SA=nil AKKOR RETURN Objektum EGYÉBKÉNT RETURN SA

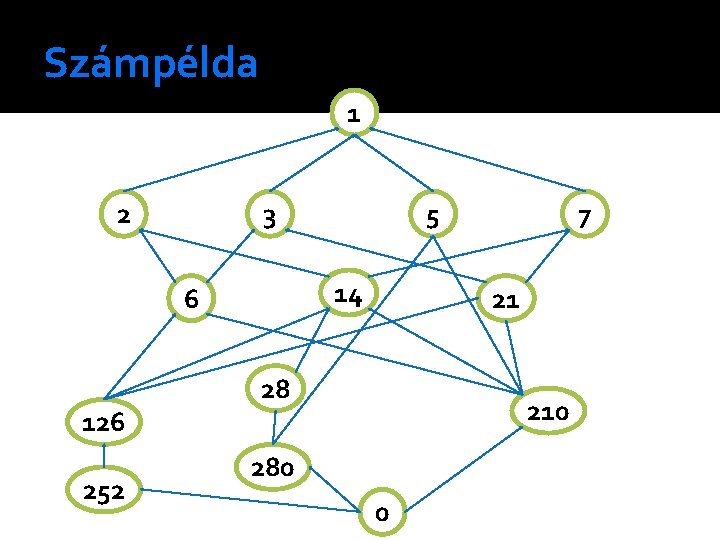
1. Példa �Legyen adott a következő alárendelési reláció: x alárendeli y-t, ha x osztója y-nak Nben. �Tekintsük a következő számokat: 1, 2, 3, 5, 6, 7, 14, 21, 28, 126, 210, 252, 280.

Számpélda 1 2 3 14 6 126 252 5 7 21 28 210 280 0

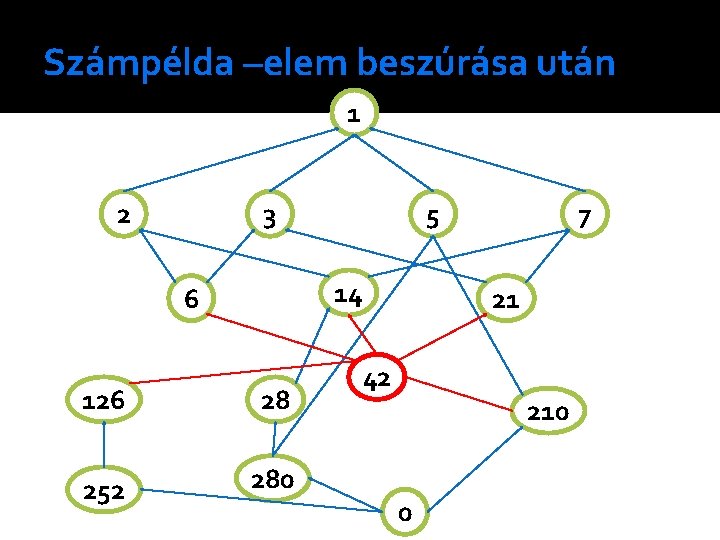
Példa �Ebbe a hierarchiába szúrjuk be számot. a 42 -es a 42 SA-i: 6, 14, és 21 a 42 AA-i: 126 és 210 a 210 -ből a 6 felé, 126 -ból a 6, 14, 21 felé mutató éleket töröltük

Számpélda –elem beszúrása után 1 2 3 5 14 6 126 28 252 280 7 21 42 210 0

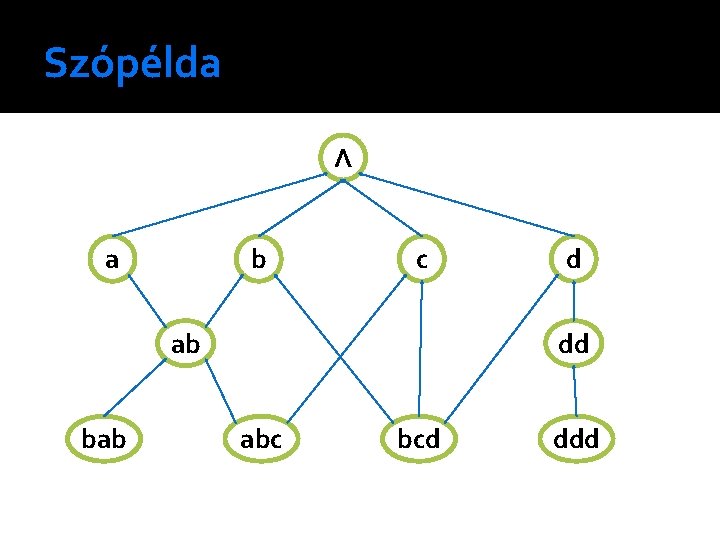
2. Példa {Λ, a, abc, b, bab, bcd, c, d, ddd}, ahol �Λ, amely az üres szót jelenti, a hierarchia gyökere. A szavak egy halmaza egy osztályba sorolható, ha a szavak mindegyike tartalmaz az {a, b, c, d} abécén definiált motívumot. Az osztály nevét az őt jellemző motívum adja.

Példa Például: ab = (motif, *ab*) ahol motif az attribútum neve és * jelöl egy tetszőleges karakterláncot. Definiáljuk az alárendelési relációt két osztály között úgy hogy x ⊑ y, ha az y motif része részszó az x motif részében, azaz, ha x előállítható mym′ alakban, ahol m és m′ két szó.

Szópélda Λ a b c ab bab d dd abc bcd ddd

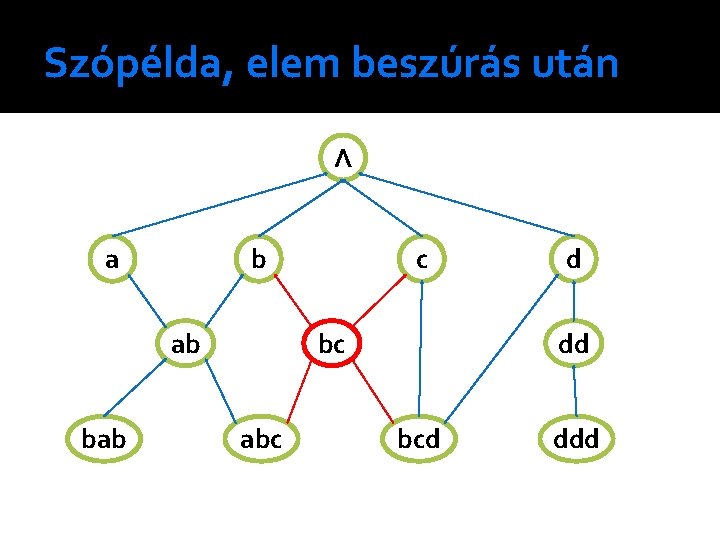
Példa �A következő ábrán a bc szó beszúrása utáni állapot látható. �A bc legspecifikusabb alárendelői b és c, míg a legáltalánosabb alárendeltjei abc és bcd. Az abc-c és bcd-b éleket töröltük.

Szópélda, elem beszúrás után Λ a b ab bab c bc abc d dd bcd ddd

Összegzés Az ismeretreprezentációs rendszerekben a következtetés kihasználja a szakterületi ismereteket reprezentáló hierarchia tulajdonságait.

Összegzés A következtetések alapját az alábbi műveletek képezik: �az alárendelés ellenőrzése lehetővé teszi, hogy eldöntsük, vajon egy C osztály alárendeli-e a D osztályt �az osztályok klasszifikációja során egy új X osztályt a neki megfelelő sorrend szerint elhelyezünk a H hierarchiába

Összegzés A következtetések alapját az alábbi műveletek képezik: �az egyedek osztályozása során meghatározzuk azt az osztályt, amelynek az adott x objektum egyede lehet �a tulajdonságok keresésének a célja, hogy megtaláljuk egy osztály vagy egyed tulajdonságait, illetve a tulajdonságokhoz és azok értékeihez tartozó korlátozásokat