Introduccin a la estadstica Algunas definiciones de estadstica

Introducción a la estadística Algunas definiciones de estadística • Ciencia de tomar decisiones en presencia de la incertidumbre. Freund, J. E. – Eallis y Roberts • § Rama del conocimiento científico que se ocupa del análisis numérico e interpretación de los resultados que provienen de experimentos de naturaleza aleatoria. Capelletti, C. A. • § Disciplina que investiga la posibilidad de extraer de los datos inferencias válidas, elaborando los métodos mediante los cuales pueden obtenerse dichas inferencias. Cramer, H. • § Ciencia de tomar decisiones en base a observaciones. Sprowls, C. • § Operación de análisis matemático que permite estudiar con el máximo de precisión los fenómenos no conocidos completamente. Mothes, J. • § Disciplina que trata los problemas relativos a las características operatorias de las reglas de comportamiento inductivo, basadas en experimentos aleatorios. Neyman, J.

Introducción a la estadística • Estadística descriptiva. • Estadística inferencial. • Relación entre variables, de acuerdo a los distintos niveles de medición. • Técnicas de análisis de asociación entre variables de distintos niveles de medición. • Lógica de los test de hipótesis.

Sistema de Información Estadística • Un Sistema de Información Estadística • “Conjunto de reglas, principios, métodos y actividades ordenadamente relacionados entre sí, que permiten observar y evaluar mediante mediciones periódicas o permanentes y desde un punto de vista cuantitativo, recursos, actividades, resultados y acciones realizadas dentro de un sector, una entidad o de un conjunto de sectores o de entidades ”.

Estadística • Describir nuestro conjunto de datos: Características, valores atípicos, dispersión, tendencias para datos temporales. • Descubrir patrones de comportamiento en los datos o ciertas relaciones entre las variables medidas. • Intentar extrapolar la información contenida en la muestra a un conjunto mayor de datos. • Inferir futuros comportamientos de la población estudiada (predicción)

Estadística: clasificaciones • Estadística descriptiva • Estadística inferencial • Estadística exploratoria • Estadística multivariada • Estadística no paramétrica

Niveles de medición • Nominal: El valor de la variable indica solo la clase de pertenencia • Ordinal: Las clases de pertenencia pueden ser ordenadas. • Intervalo: El valor de la variable tiene un sentido y en general podremos (en al mayoría de los casos) calcular promedios, medidas de dispersión y aplicar test. Pero no siempre podremos establecer razones ente dos valores de la variable. • Razón: Existe un cero absoluto, podemos efectuar cocientes de los valores de la variable.

Resumen de información • Estadísticos de posición o locación: ¿Donde esta ubicado nuestro conjunto de datos? – Modo – Mediana – Media • Estadísticos de dispersión – Rango – Coeficiente de variación

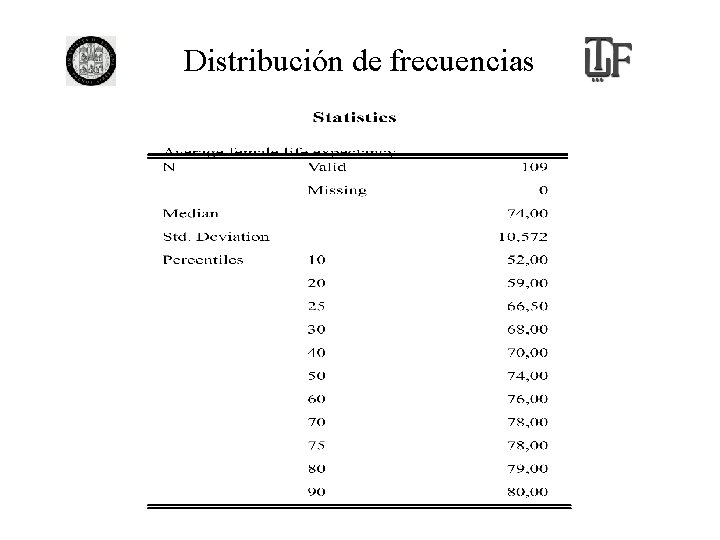
Distribución de frecuencias

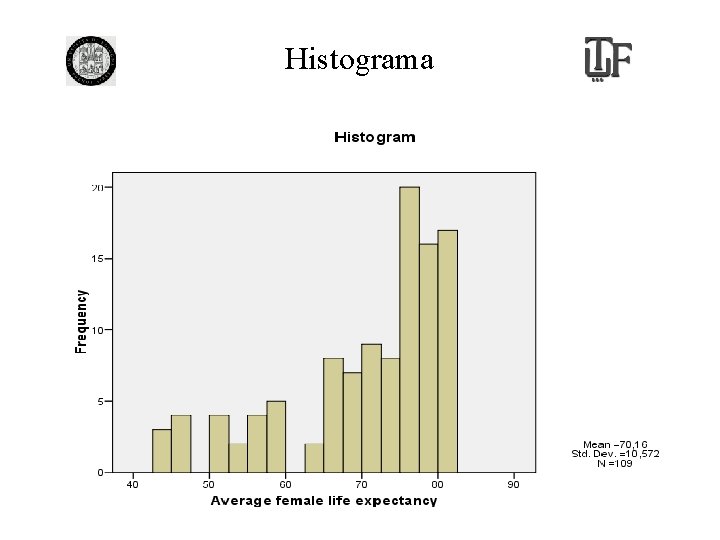
Variables cuantitativas: medidas de posición • Modo. • Mediana y percentiles • Media: promedio de la variable • El uso de estos estadisticos depende de los objetivos del analista o de las características de la población que se desea estudiar.

Histograma

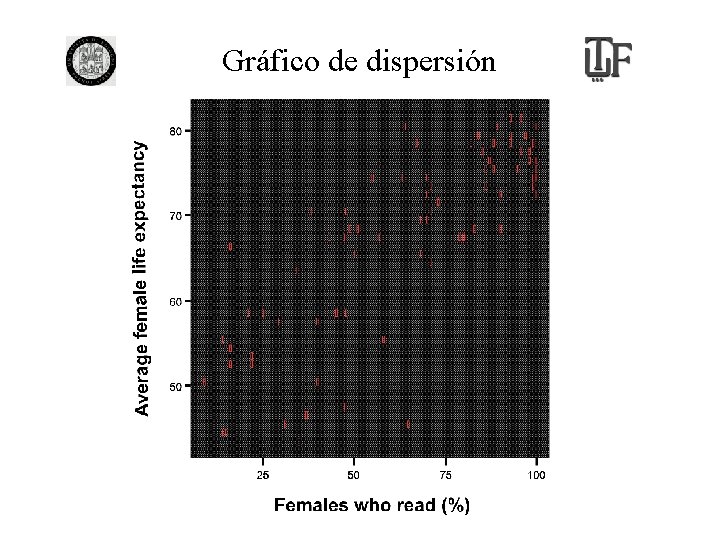
Gráfico de dispersión

Pirámides de población

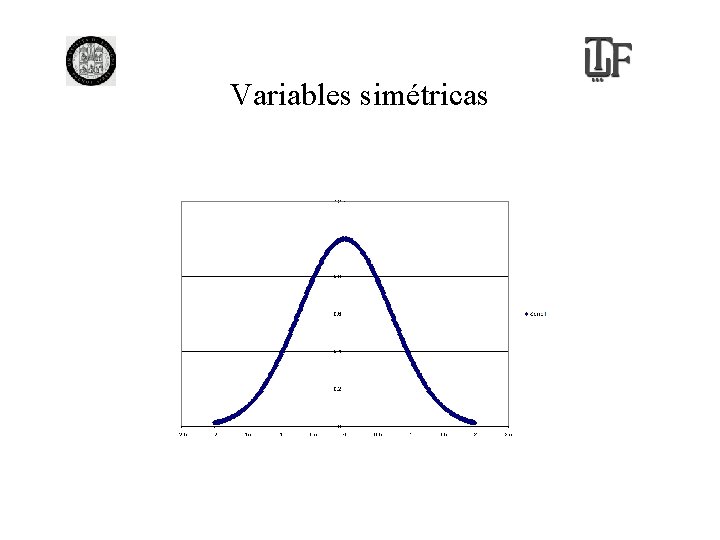
Variables simétricas

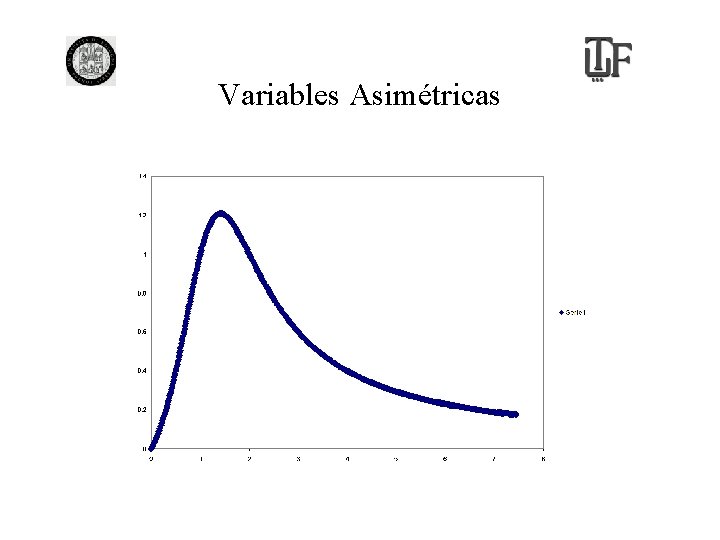
Variables Asimétricas

Medidas de asimetría • La medida más usual de asimetría: “skewness” • Cuando se tiene variables asimétricas con valores positivos (ingreso por ejemplo), es usual tomar logaritmo para simetrizarlas.

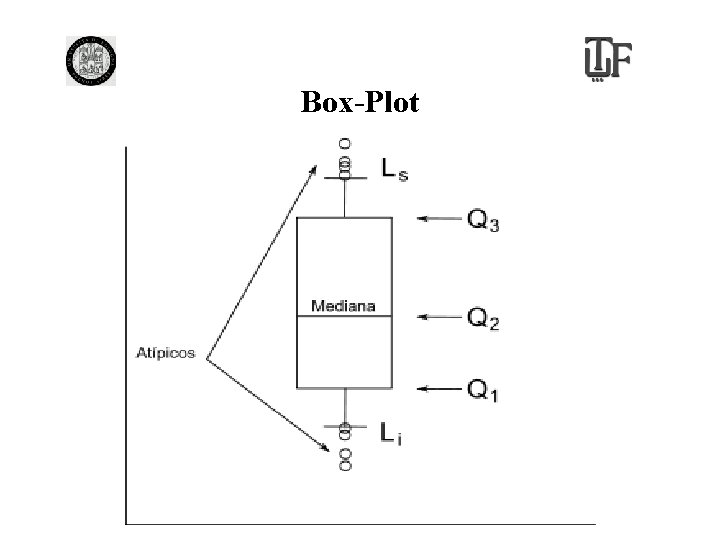
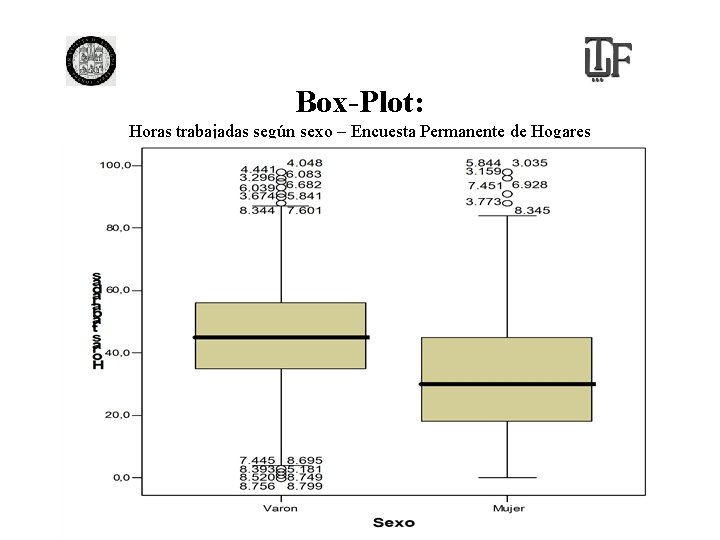
Box-Plot

Box-Plot: Horas trabajadas según sexo – Encuesta Permanente de Hogares

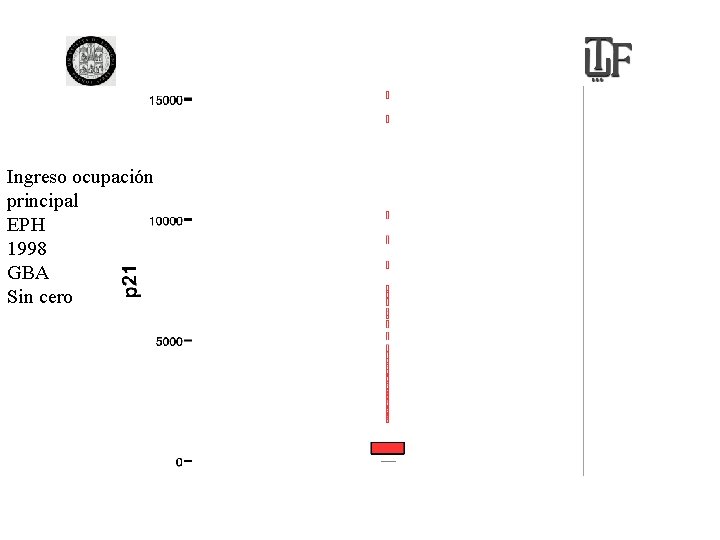
Ingreso ocupacion principal EPH 1998 GBA

Ingreso ocupación principal EPH 1998 GBA Sin cero

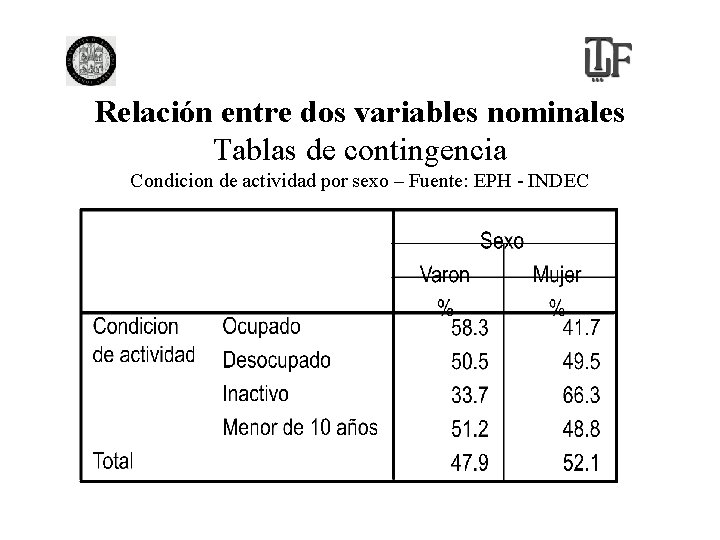
Relación entre dos variables nominales Tablas de contingencia Condicion de actividad por sexo – Fuente: EPH - INDEC

Relación entre dos variables nominales: Tablas de contingencia • Hipótesis nula: no existe asociación estadistica entre las dos variables, la distribución de los efectivos es proporcional a los “marginales”: totales fila y columna. • Hipotesis alternativa: existe asociación estadística entre las variables

Tablas de contingencia Test de Chi – Cuadrado • Chi-cuadrado: Compara los efectivos teóricos (bajo el supuesto de independencia) con los observados. • Efectivos teóricos en la celda (i, j):

Chi-cuadrado • Si los observados son iguales a los teóricos, el coeficiente vale cero. • El coeficiente aumenta al aumentar la discrepancia entre el observado y el teórico, respecto al valor teórico. • Pero este coeficiente depende de n: Aumenta con el número de observaciones.

Chi-cuadrado normalizado - PHI • Se cumple que <=min(J-1, I-1)

V de Cramer • Donde m = min(L-1, K-1) • Se cumple que 0<=V<=1

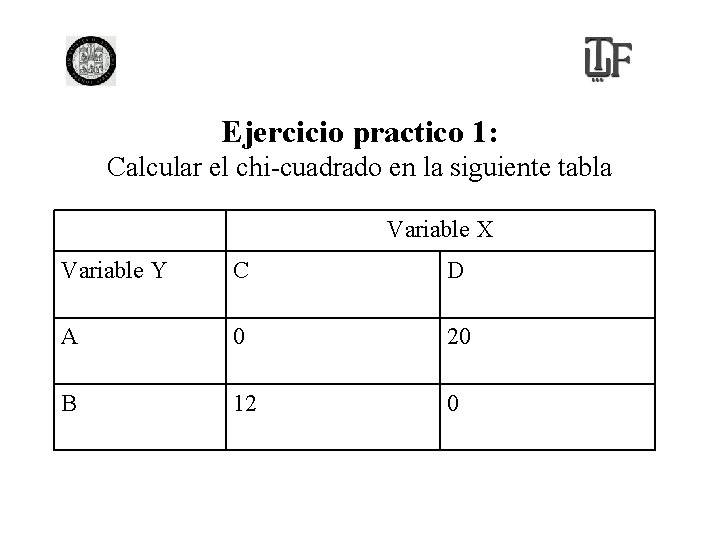
Ejercicio practico 1: Calcular el chi-cuadrado en la siguiente tabla Variable X Variable Y C D A 0 20 B 12 0

Ejercicio practico 2: Calcular el chi-cuadrado y el V de Cramer en la siguiente tabla Variable X Variable Y C D A 0 200 B 120 0

Asociación entre variables ordinales y cuantitativas: Coeficientes de correlación • Estos coeficientes reflejan en general el hecho de que una de las variables aumenta de valor cuando la otra lo hace. • Los más utilizados: – Coeficiente de correlación de Pearson (Karl Pearson, 1857 -1936) – Coeficiente de correlación de Spearman (Charles Spearman, (1863 -1945)

Coeficiente de correlación de Pearson entre dos variables X e Y ρ = Cov(X, Y)/DS(X)*DS(Y) • Variables continuas (de razón). • Mide la existencia de una relación lineal entre las variables. • -1 <= ρ <= 1 • ρ =0 : ausencia de relación lineal • ρ =1: relación lineal creciente • ρ =-1: relación lineal decreciente • Sensible a valores extremos o atípicos

Coeficiente de correlación de Pearson: significado • El ρ de Pearson indica la existencia de una relación lineal entre X e Y. • Identifica relaciones positivas y negativas. El coeficiente 0 indica ausencia de relacion estadística • Puede haber una relación creciente, pero no lineal.

Ejercicio practico 3: Coeficiente de correlación de Pearson • Hallar el ρ de Pearson para la siguiente serie de valores. Graficarla con Excel. X 1 2 3 4 Y 1 4 9 16

Coeficiente de correlación de Spearman entre dos variables X e Y rs = ρ(rang(X), rang(Y)) • Variables ordinales. • Mide la existencia de una relación creciente o decreciente entre las variables. • -1 <= ρ <= 1 • ρ =0 : ausencia de relación creciente o decreciente • ρ =1: relación creciente • ρ =-1: relación decreciente • Robusto a valores extremos o atípicos

Coeficiente de correlación de Spearman entre dos variables X e Y • En caso de rangos “empatados”, tomamos el promedio de los rangos.

Ejercicio práctico 4: Asociación entre dos variable ordinales y cuantitativas • Dada el siguiente par de valores de dos variables, comprobar que el coeficiente de correlación de Spearman es el coeficiente de correlación de Pearson de los rangos . X Y 4 7 3 2 1 2 5 3 2 2

Recta de regresión • Supongamos tener n obervaciones bivariadas, o sea a cada elemento le medimos un par de variables (Xi, Yi) que supondremos continuas por ahora. – – Peso y estatura. Producto Bruto Per capita y Tasa de mortalidad infantil. Tasa de desempleo y ingreso medio de los asalariados Cigarrillos fumados por día y probabilidad de sufrir cáncer de pulmón.

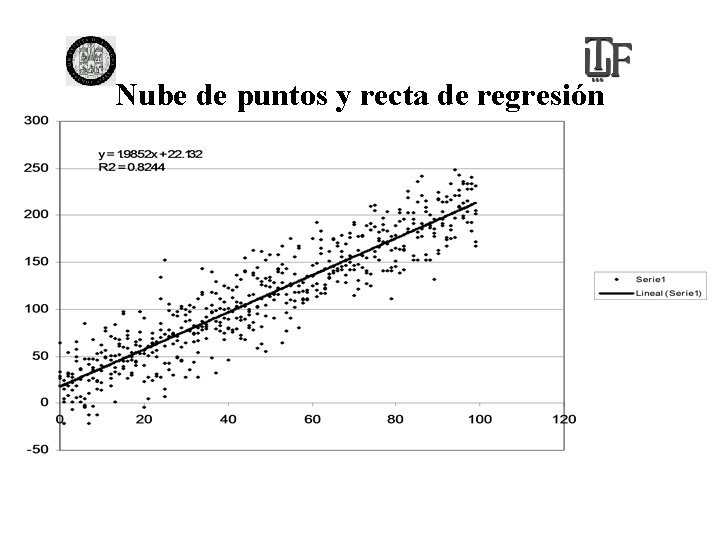
Recta de regresión: Ejemplo • En el siguiente gráfico se muestran los 8511 radios censales del Gran Buenos Aires. A cada radio se le midieron dos variables: % de hogares con celular y % de hogares con freezer, según datos del CENSO 2001. • Los datos se graficaron mediante un gráfico X-Y. • El eje de las X (horizontal) indica al % de hogares con freezer, el eje de las Y (vertical) el % de hogares con celular. • Vemos que hay una relación aproximadamente lineal entre ambas variables, por lo menos en la parte central del gráfico.

Nube de puntos y recta de regresión

Modelo de regresión • La relación puede ser lineal solo en una parte del recorrido de las variables. • Variable X: variable “independiente” o explicativa. • Variable Y: variable “dependiente” o explicada. • El modelo de regresión no implica “causalidad” (ej. Educación e Ingreso). • El modelo de regresión puede tener más de una variable: explicativa: modelo de regresión múltiple.

Modelo de regresión: Forma general • El modelo subyacente en la regresión lineal (simple o múltiple) es que la variable dependientes una función lineal de las variables independientes: • Y= 1+b 1·X 1+b 2·X 2+…bk·Xk + e. • e es una variable aleatoria, pues no es razonable suponer una relación lineal exacta entre Y y X 1, …, Xk • Pero en promedio podemos suponer que e será igual a cero. • e se denomina el término de errror. Es igual a la diferencia entre el valor observado y la recta de regresión.

Ajuste del modelo de regresión • Por ajuste del modelo de regresión se interpreta cuan bien la “nube de puntos” está cerca de la recta de regresión. • El modelo de regresión tiene una medida de la “bondad de ajsute”: el R 2. Este valor está entre 0 y 1. • 1 -> Ajuste perfecto • 0 -> No hay efecto de las variables independientes y la variable dependiente. • No todos los modelos en estadística poseen una medida objetiva del “ajuste” de los datos al modelo.

Ajuste del modelo de regresión • Supongamos el modelo de regresión simple • Y= a + b*X + e – El “parámetro“ b indica cuánto aumenta Y por un aumento unitario de X. – Si X no tiene efecto sobre Y, b valdrá 0. . – a es la ordenada al origen.

Ajuste del modelo de regresión • Los paquetes estadísticos o Excel nos proveen estadísticos para evaluar el ajuste del modelo (R 2). • Y para evaluar si b es “significativamente distinto de cero” o no. . . Si es “significativamente distinto de cero”, la variable independiente X tiene un efecto sobre Y.

Ajuste del modelo de regresión • En general, si el tamaño de muestra es muy grande, los parámetros pueden ser “significativamente distintos de cero” a menudo. • Esto no significa que sean relevantes para el investigador.

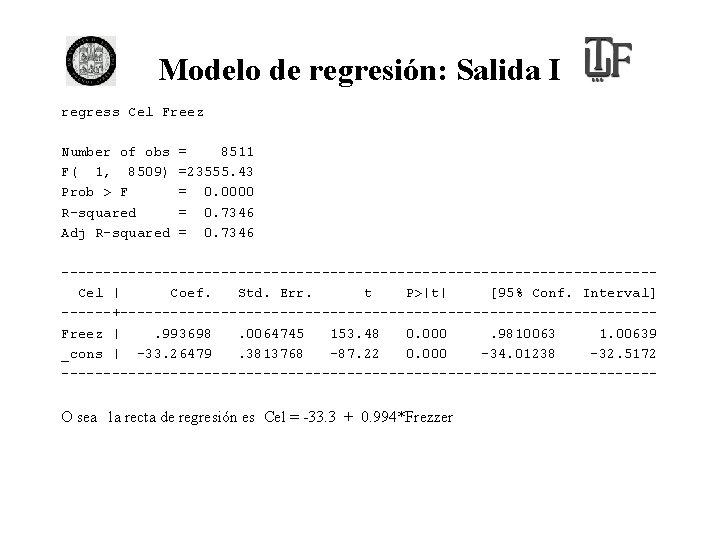
Recta de regresión: Cálculo de los parámetros • Para el ejemplo anterior son los 8511 radios censales, se plantea el modelo que explica a la variable CEL (% de celulares). • Cel = a + b*Freezer + e • Con el paquete Stata se calcularon los parámetros a y b. La salida es la siguiente:

Modelo de regresión: Salida I regress Cel Freez Number of obs F( 1, 8509) Prob > F R-squared Adj R-squared = 8511 =23555. 43 = 0. 0000 = 0. 7346 -----------------------------------Cel | Coef. Std. Err. t P>|t| [95% Conf. Interval] ------+--------------------------------Freez |. 993698. 0064745 153. 48 0. 000. 9810063 1. 00639 _cons | -33. 26479. 3813768 -87. 22 0. 000 -34. 01238 -32. 5172 ------------------------------------ O sea la recta de regresión es Cel = -33. 3 + 0. 994*Frezzer

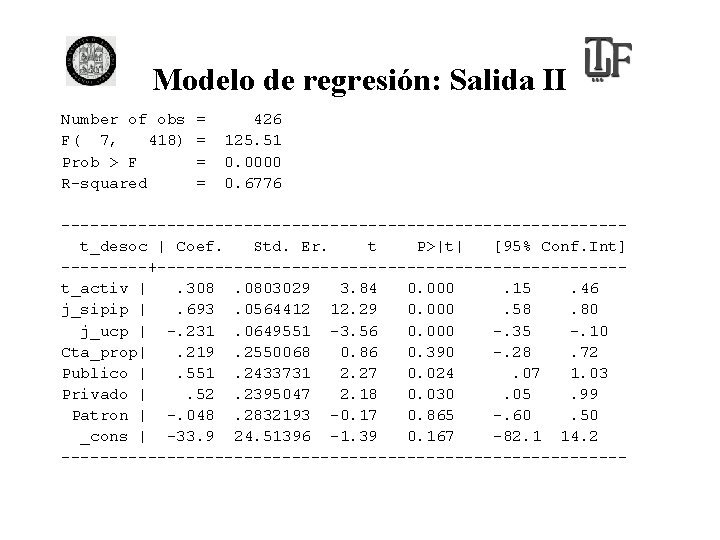
Modelo de regresión: Salida II Number of obs F( 7, 418) Prob > F R-squared = = 426 125. 51 0. 0000 0. 6776 -----------------------------t_desoc | Coef. Std. Er. t P>|t| [95% Conf. Int] -----+------------------------t_activ |. 308. 0803029 3. 84 0. 000. 15. 46 j_sipip |. 693. 0564412 12. 29 0. 000. 58. 80 j_ucp | -. 231. 0649551 -3. 56 0. 000 -. 35 -. 10 Cta_prop|. 219. 2550068 0. 86 0. 390 -. 28. 72 Publico |. 551. 2433731 2. 27 0. 024. 07 1. 03 Privado |. 52. 2395047 2. 18 0. 030. 05. 99 Patron | -. 048. 2832193 -0. 17 0. 865 -. 60. 50 _cons | -33. 9 24. 51396 -1. 39 0. 167 -82. 1 14. 2 ------------------------------

Ajuste del modelo de regresión • Por ajuste del modelo se interpreta cuan bien los valores observados se ajustan a nuestro modelo. • En el modelo de regresión lineal hay un estadístico, el R 2 que nos indica la bondad del ajuste. R 2 está comprendido entre 0 y 1. 1 indica un ajuste perfecto: todas las observaciones están sobre una recta.

Prueba de los coeficientes • Otra pregunta que el investigador se plantea es si algún coeficiente es igual a cero. O si es “significativamente distinto de cero”. Esta pregunta puede ser respondida mediante el estadístico t de Student. • Cuanto más grade es t, mayor la probabilidad de que el coeficiente correspondiente sea igual a cero.

Análisis de los residuos • Luego está el análisis de los residuos observados: observaciones con residuos elevados en valor absoluto pueden indicar errores de medición, puntos extremos, o un modelo especificado incorrectamente. • En general los paquetes estadísticos traen opciones para graficar los residuos y detectar aquellos con valores grandes. • Finalmente, corresponde al investigador social interpretar si el modelo es plausible, que significan los parámetros, explicar el porquébuna observación tiene un residuo excesivamente grande, mantener o eliminar una variable.

Tipo de variables en el modelo de regresión lineal • El modelo de regresión se plantea en general cuando la variable dependiente (Y) es continua • En teoría, las variables explicativas (X) pueden ser todas nominales (por ejemplo en un modelo que explique el ingreso sexo, tramo de edad, etc. ). • Cuando la variable a explicar (Y) no es continua, debemos aplicar otro modelo (Poisson, logit, etc)

Ejercicio practico 4: Regresión lineal simple • Para los siguientes datos, calcular los coeficientes de regresión mediante el programa EXCEL. X 2 5 10 40 Y 34 33 21 39

Ejercicio práctico 4:

Universo, población y muestra • Universo, población, muestra. • Parámetros poblacionales. • Estimación a partir de una muestra: Inferencia y estimadores. • Propiedades de los estimadores.