ESTADSTICA DESCRIPTIVA Introduccin La Estadstica es una ciencia

ESTADÍSTICA DESCRIPTIVA

Introducción La Estadística es una ciencia que facilita la solución de problemas en los cuales necesitamos conocer características sobre el comportamiento de algún suceso o evento. Nos permite inferir el comportamiento de sucesos iguales o similares sin necesidad de que estos ocurran.

Esto nos da la posibilidad de tomar decisiones acertadas y a tiempo, así como realizar proyecciones del comportamiento del suceso. Sólo se realizan los cálculos y el análisis con los datos obtenidos de una muestra de la población y no con toda la población.

¿Por qué hay que conocer la Estadística y quiénes la utilizan? Está presente en todas las áreas del saber humano. Lo utilizan médicos, banqueros, deportistas, amas de casa. Es una herramienta fundamental en la investigación. Permite realizar una buena toma de decisiones.

Actualmente el DANE es el encargado de concentrar y publicar la información estadística del país.

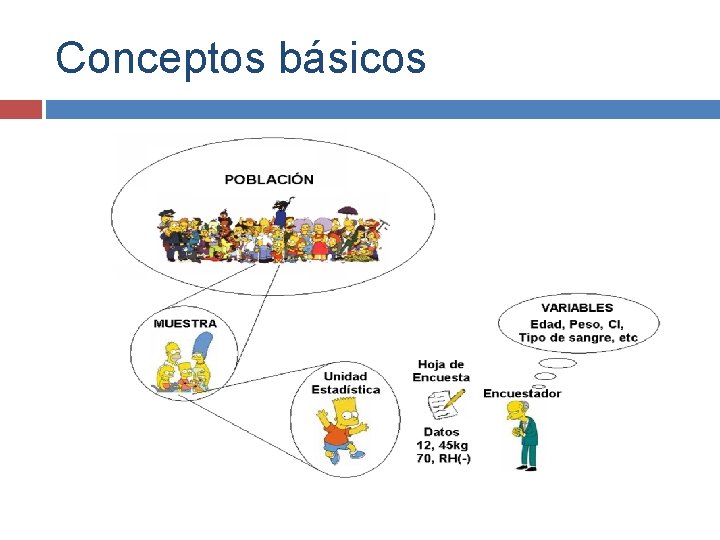
Conceptos básicos

La ESTADISTICA es la ciencia que se ocupa de la • Sistematización, recogida, ordenación y presentación de los datos referentes a un fenómeno que presenta variabilidad o incertidumbre para su estudio metódico, con objeto Descriptiva • deducir las leyes que rigen esos fenómenos, Probabilidad • y poder de esa forma hacer previsiones sobre los mismos, tomar decisiones u obtener conclusiones. Inferencia

Estadística: Es la ciencia que se encarga de recolectar, organizar, resumir y analizar datos para después obtener conclusiones. Se divide en Estadística Descriptiva y Estadística Inferencial. descriptiva: Estadística Se encarga de la recolección, organización, presentación y análisis de los datos de una población.

Estadística inferencial: Se encarga de analizar la información presentada por la estadística descriptiva mediante técnicas que nos ayuden a conocer, con determinado grado de confianza, a la población. Lo que nos permite tomar decisiones.

Población: Conjunto definido de TODOS los INDIVIDUOS, de donde se observa cierta característica. Al número de integrantes de la población se llama tamaño de la población y se representa con la letra N. Las poblaciones pueden ser finitas o infinitas.

Población Estadística: Conjunto de TODOS los DATOS que se obtienen al realizar la medición de una variable en los elementos de una población. Muestra: Subconjunto de una población, que intenta reflejar las características de la población lo mejor posible. El número de individuos que integran la muestra, llamado tamaño de la muestra se representa con la letra n.

Individuo: Es el elemento de la población o de la muestra que aporta información sobre lo que se estudia. Variable: Característica o propiedad de los individuos que se desea estudiar y se puede medir o calificar; cambia o varía con el tiempo en un individuo dado, o cambia o varía de elemento a elemento. Ej. Edad, peso, sexo, estado civil, número de

Dato: Valor que se obtiene al realizar la medición de la característica de la variable en estudio. Pueden ser univariados, bivariados o multivariados. La naturaleza de los datos pueden ser datos cuantitativos o datos cualitativos.

Datos Cuantitativos (números): Valores obtenidos al medir peso, estatura, temperatura, número de hijos. Datos Cualitativos (categorías): Se obtienen al calificar la característica en cuestión como el sexo, estado civil, grado máximo de estudios.

Variable Dicotómica: Sólo puede tomar dos valores (sí – no, 0 – 1, hombre – mujer, bueno – malo, encendido – apagado). En la variable CUANTITATIVA se pueden distinguir dos tipos: continua y discreta.

Variable Continua: Si la variable puede tomar cualquier número real entre dos valores dados (decimal o entero). Ej. El peso de un individuo. Variable Discreta: Si la variable sólo puede tomar números enteros. Ej. El número de hijos de un individuo.

Escalas de Medición Escala Nominal Escala Ordinal Escala de Intervalo Escala de Razón

Escala Nominal: Está asociada a variables cualitativitas y es denominada de este modo si no se pueden hacer operaciones aritméticas entre sus valores, pues éstos son únicamente ETIQUETAS. Ejemplo: sexo, código postal, estado civil, número telefónico, número al correr en un maratón, deporte favorito, carrera a estudiar, etc.

Escala Ordinal: Los valores de la variable que tienen un ORDEN con un nivel específico, pero no se pueden hacer operaciones aritméticas entre ellas. Ejemplo: Pésimo – Malo – Regular – Bueno – Excelente Primaria – Secundaria – Preparatoria Licenciatura

Escala de Intervalo: En ella existe un orden entre los valores de la variable y además una NOCIÓN DE DISTANCIA aunque no se puedan realizar operaciones. El cero o punto de inicio no es único, es más bien un punto de referencia. Ejemplo: Escalas de temperatura, la edad de la Tierra, la línea del tiempo de la humanidad.

Escala de Razón: La magnitud tiene SENTIDO FÍSICO, existe el cero absoluto, existe orden, se puede determinar cuántas veces es mayor uno que otro. Ejemplo: peso, estatura, edad, distancia, dinero, etc.

Fuentes de información Encuesta: Recopilar los datos mediante el uso de cuestionarios o entrevistas. Experimento: Procedimiento utilizado en la investigación científica para obtener información que permita conocer el comportamiento de algún proceso.

Fuentes de Información Investigación Documental: Procedimiento para obtener datos mediante la consulta de información ya escrita y concentrada en documentos que se localicen en libros o revistas en bibliotecas, hemerotecas, o en centros virtuales.

Redondeo de datos, notación científica y cifras significativas. Redondeo: El redondeo de datos es un procedimiento que consiste en escribir un número que representa a una cantidad con menos cifras de las que tiene realmente para tener una idea rápida de la cantidad.

Notación Científica Es una manera de escribir en forma breve cifras muy grandes o pequeñas. La forma n es general a x 10 , en donde “a” es un número entre 1 y 9, “n” es un número entero. 4 Ejemplo: 4 El número 25 000 se escribe 2. 5 x 10 , o el número 0. 00025 se escribe como 2. 5 x 10.

Cifras Significativas A los dígitos exactos que se utilizan para escribir una cifra, a parte de los ceros para localizar el punto decimal, se les llama cifras significativas. Ejemplos: 3. 22 tiene 3 cifras significativas. -3 0. 0032 = 3. 2 x 10 tiene 2 cifras significativas. -3 0. 00320 = 3. 20 x 10 tiene 3 cifras significativas.

La cifra 3. 22 se encuentra realmente entre 3. 215 y 3. 225. La cifra 0. 0032 es un valor que se encuentra entre 0. 00315 y 0. 00325. La cifra 0. 00320 se encuentra entre las cifras 0. 003195 y 0. 003205

Orden de datos La ordenación es el proceso mediante el cual los datos están acomodados de tal manera que se establece un orden (ascendente o descendente) entre ellos. Hay dos métodos comunes: • Listado en orden • ascendente Método de tallo y hojas

Ejemplo Considera que la variable de estudio es el peso de 25 estudiantes. Los pesos se encuentran en la siguiente tabla: Peso de 25 estudiantes (en kg) 40 56 52 63 57 43 44 62 50 66 48 42 44 56 63 51 55 50 55 51 49 52 59 45 58

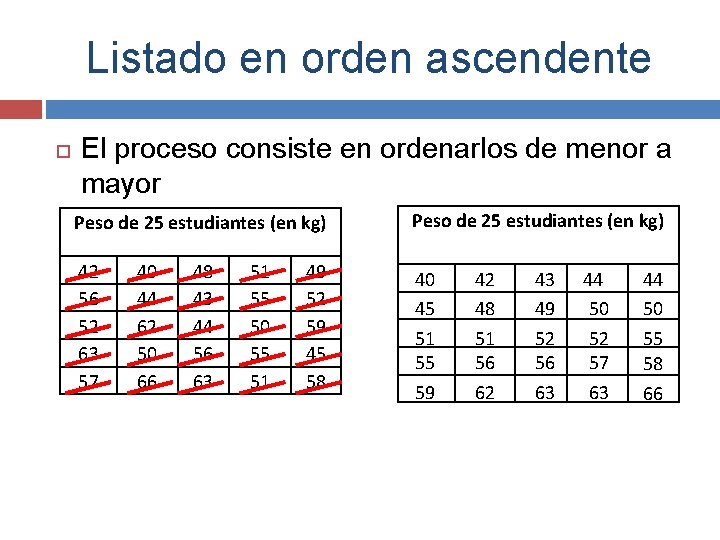
Listado en orden ascendente El proceso consiste en ordenarlos de menor a mayor Peso de 25 estudiantes (en kg) 42 56 52 63 57 40 45 51 55 59 40 44 62 50 66 48 43 44 56 63 51 55 50 55 51 49 52 59 45 58 42 48 51 56 62 43 49 52 56 63 44 50 52 57 63 44 50 55 58 66

Método de tallo y hojas Si los números de los datos están formados por dos dígitos, se hace una columna con el primer dígito (decenas) y a la derecha de cada uno de ellos se escribe, en fila, sólo el segundo dígito (unidades) de cada uno de los datos que tengan el mismo primer dígito.

Datos sin ordenar: 2, 0, 8, 9, 4, 3, 4, 5 1, 6, 5, 2, 2, 0, 9, 0, 6, 5, 7, 1, 8 2, 3, 6, 3 4 5 6 Datos ordenados: 4 5 6 Peso de 25 estudiantes (en kg) 42 56 52 63 57 40 44 62 50 66 48 43 44 56 63 0, 2, 3, 4, 4, 5, 8, 9 0, 0, 1, 1, 2, 2, 5, 5, 6, 6, 7, 8, 9 2, 3, 3, 6 51 55 50 55 51 49 52 59 45 58

Doble tallo Una variante de este método es en lugar de dividir en un grupo las decenas, se divide en dos grupos. El primero abarcando los dígitos del 0 al 4 y el segundo del 5 al 9. El ejemplo anterior queda: 4 4 5 5 6 6 0, 2, 3, 4, 4 5, 8, 9 0, 0, 1, 1, 2, 2, 5, 5, 6, 6, 7, 8, 9 2, 3, 3 6

Caso de variables cualitatitivas El procedimiento es: Se identifican todos los valores diferentes y se acomodan en columna. Se agrega una segunda columna en donde se van registrando, mediante una línea vertical, la veces que aparece el valor dado.

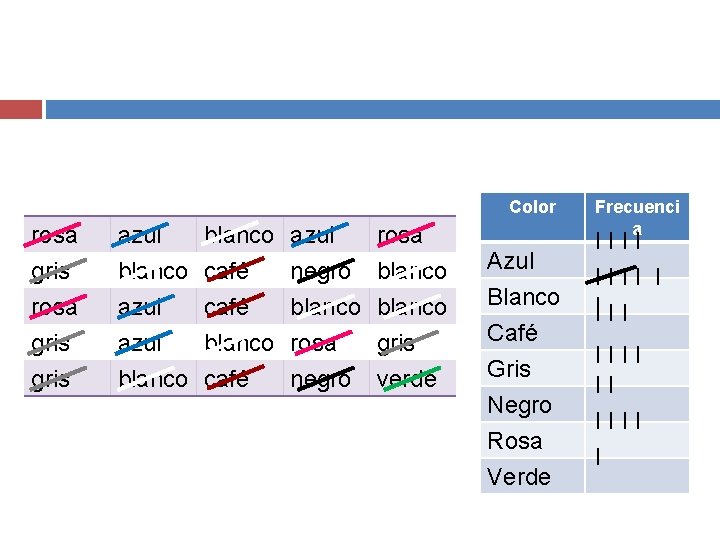
Ejemplo Considera que la variable de estudio es el color de playera de 25 estudiantes. Los colores se encuentran en la siguiente tabla: rosa gris azul blanco café blanco azul negro blanco rosa blanco gris blanco café negro verde

Color rosa gris azul blanco café blanco gris blanco café azul negro blanco rosa blanco gris negro verde Azul Blanco Café Gris Negro Rosa Verde Frecuenci a IIII I I IIII I

Tabla de Frecuencia de Datos Una vez que se tenga ordenados los datos, se acomodan en la “Tabla de distribución de frecuencias o tabla de frecuencias”. La tabla es básicamente una tabla de valores x-y, dónde “x” representa el dato y “y” representa la frecuencia.

La frecuencia es el número de veces que aparece cada dato. Hay dos clases de tablas de frecuencias: Para datos NO agrupados. Para datos agrupados.

Tabla de frecuencias para datos NO agrupados Está formada por dos columnas: una para la variable “xi” y la otra para su frecuencia “f”, a esta frecuencia se le llama frecuencia absoluta o frecuencia observada.

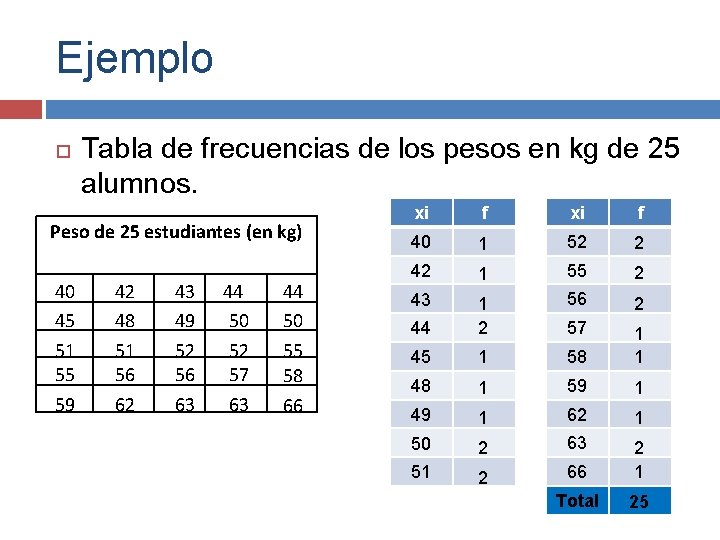
Ejemplo Tabla de frecuencias de los pesos en kg de 25 alumnos. Peso de 25 estudiantes (en kg) 40 45 51 55 59 42 48 51 56 62 43 49 52 56 63 44 50 52 57 63 44 50 55 58 66 xi f 40 1 52 2 42 1 55 2 43 56 2 44 1 2 57 45 1 58 1 1 48 1 59 1 49 1 62 1 50 2 63 51 2 66 2 1 Total 25

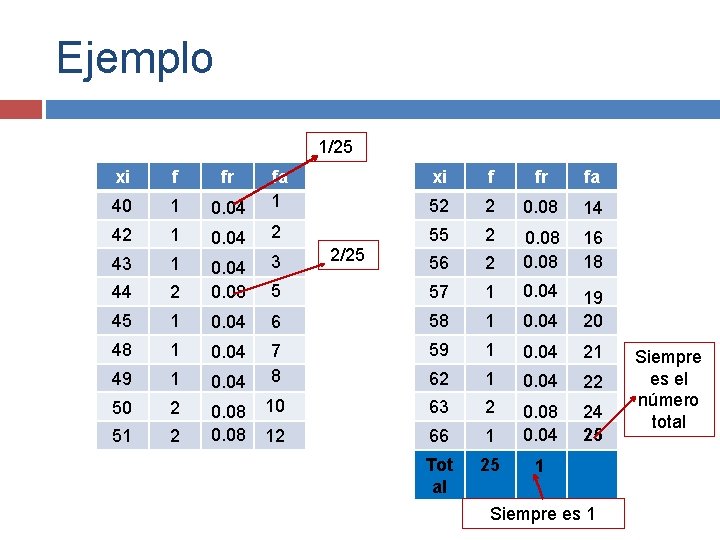
Frecuencia relativa y acumulada Por lo regular, se agregan dos columnas: la de la frecuencia relativa “fr” y la de la frecuencia acumulada “fa”. La frecuencia relativa se obtiene mediante el cociente de la frecuencia y el número total de datos, esto es fr = f/n. La frecuencia acumulada se obtiene sumando las frecuencias anteriores a las frecuencias de un dato dado.

Ejemplo 1/25 xi f fr fa 0. 04 fa 1 52 2 0. 08 14 1 0. 04 2 55 2 43 1 3 56 2 16 18 44 2 0. 04 0. 08 5 57 1 0. 04 45 1 0. 04 6 58 1 0. 04 19 20 48 1 0. 04 59 1 0. 04 21 49 1 0. 04 7 8 62 1 0. 04 22 50 2 10 63 2 51 2 0. 08 12 66 1 0. 08 0. 04 24 25 Tot al 25 1 xi f fr 40 1 42 2/25 Siempre es 1 Siempre es el número total

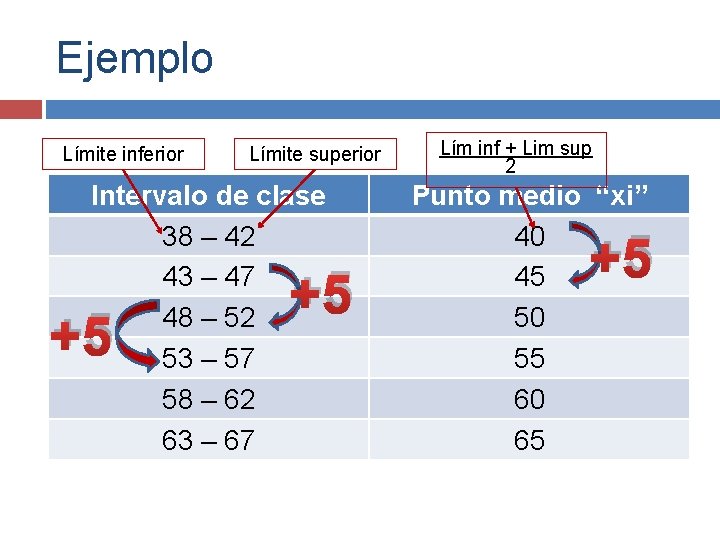
Intervalo de clase En ocasiones es conveniente acomodar los datos en pequeños grupos de igual tamaño, llamados intervalos de clase. El punto medio o marca de clase “xi”, se obtiene con: Marca de clase Límite inferior + límite 2 superior = El tamaño del intervalo se obtiene mediante la diferencia de los límites

Ejemplo Límite inferior Límite superior Intervalo de clase 38 – 42 43 – 47 48 – 52 53 – 57 58 – 62 63 – 67 +5 +5 Lím inf + Lim sup 2 Punto medio “xi” 40 45 50 55 60 65 +5

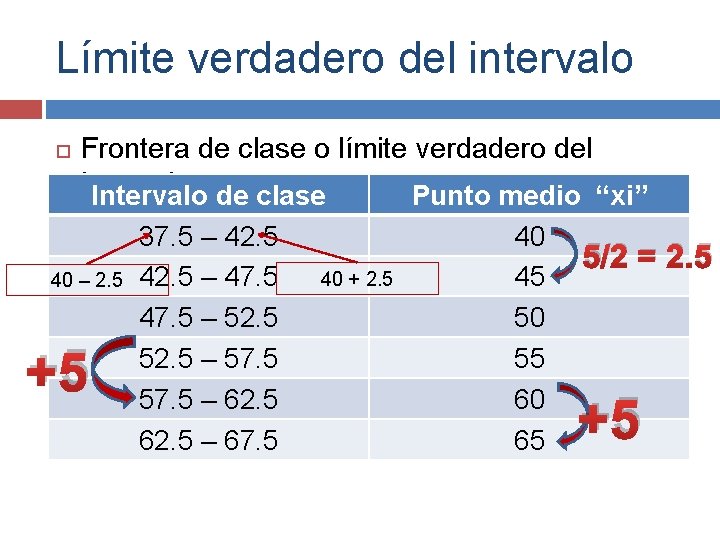
Límite verdadero del intervalo Frontera de clase o límite verdadero del intervalo: Intervalo de clase Punto medio “xi” 40 – 2. 5 +5 37. 5 – 42. 5 – 47. 5 – 52. 5 – 57. 5 – 62. 5 – 67. 5 40 + 2. 5 40 45 50 55 60 65 5/2 = 2. 5 +5

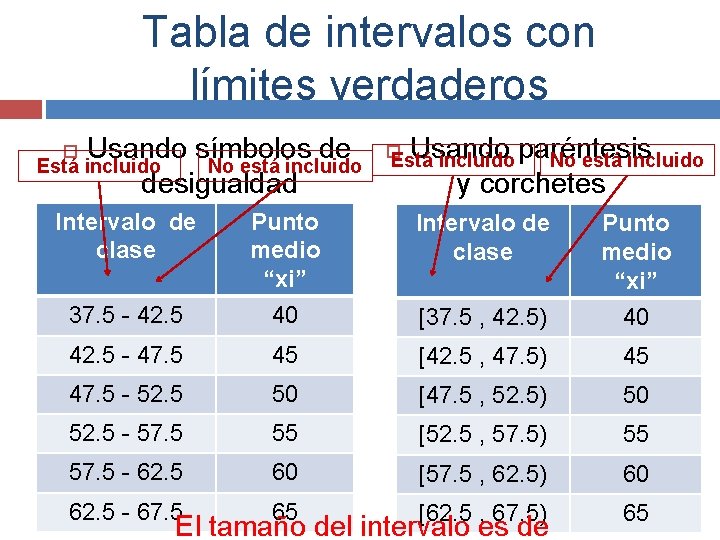
Tabla de intervalos con límites verdaderos Usando símbolos de Está incluido No está incluido desigualdad Intervalo de clase Usando Está incluido paréntesis No está incluido y corchetes Intervalo de clase 37. 5 - 42. 5 Punto medio “xi” 40 [37. 5 , 42. 5) Punto medio “xi” 40 42. 5 - 47. 5 45 [42. 5 , 47. 5) 45 47. 5 - 52. 5 50 [47. 5 , 52. 5) 50 52. 5 - 57. 5 55 [52. 5 , 57. 5) 55 57. 5 - 62. 5 60 [57. 5 , 62. 5) 60 62. 5 - 67. 5 65 [62. 5 , 67. 5) 65 El tamaño del intervalo es de

Si por alguna razón no es fácil decidir el ancho del intervalo y el número de ellos, se pueden utilizar las siguientes fórmulas: K = 1 + 3. 3 log (n) Donde K = número aproximado de clases n = número de datos. Amplitud de los intervalos = Rango / K Donde Rango = diferencia entre el dato mayor y el dato menor.

Ejemplo Para el ejemplo de los datos de los pesos de 25 alumnos, el valor de K: K = 1 + 3. 3 log (n) = 1 + 3. 3 log (25) = 5. 6. Por lo tanto se requieren aproximadamente 6 intervalos. Y la amplitud de los intervalos sería: Amplitud = Rango / K = (66 – 40) / 5. 6 = 4. 64. Aproximadamente 5 unidades es la amplitud de los intervalos.

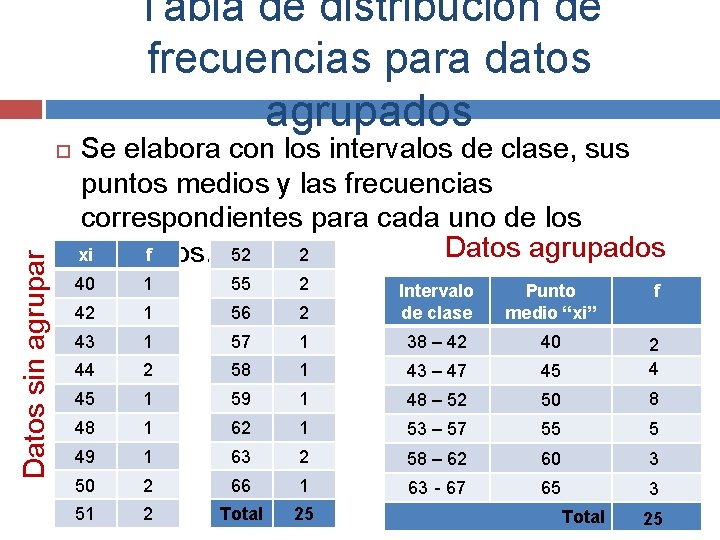
Tabla de distribución de frecuencias para datos agrupados Datos sin agrupar Se elabora con los intervalos de clase, sus puntos medios y las frecuencias correspondientes para cada uno de los Datos agrupados xi f 52 2 intervalos. 40 1 55 2 42 1 56 43 1 44 Punto medio “xi” f 2 Intervalo de clase 57 1 38 – 42 40 2 58 1 43 – 47 45 2 4 45 1 59 1 48 – 52 50 8 48 1 62 1 53 – 57 55 5 49 1 63 2 58 – 62 60 3 50 2 66 1 63 - 67 65 3 51 2 Total 25

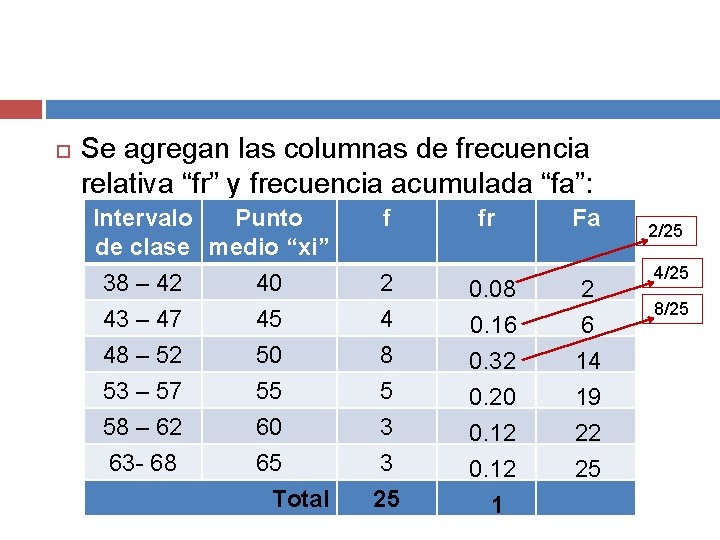
Se agregan las columnas de frecuencia relativa “fr” y frecuencia acumulada “fa”: Intervalo Punto de clase medio “xi” 38 – 42 40 43 – 47 45 48 – 52 50 53 – 57 55 58 – 62 60 63 - 68 65 Total f 2 4 8 5 3 3 25 fr 0. 08 0. 16 0. 32 0. 20 0. 12 1 Fa 2 6 14 19 22 25 2/25 4/25 8/25

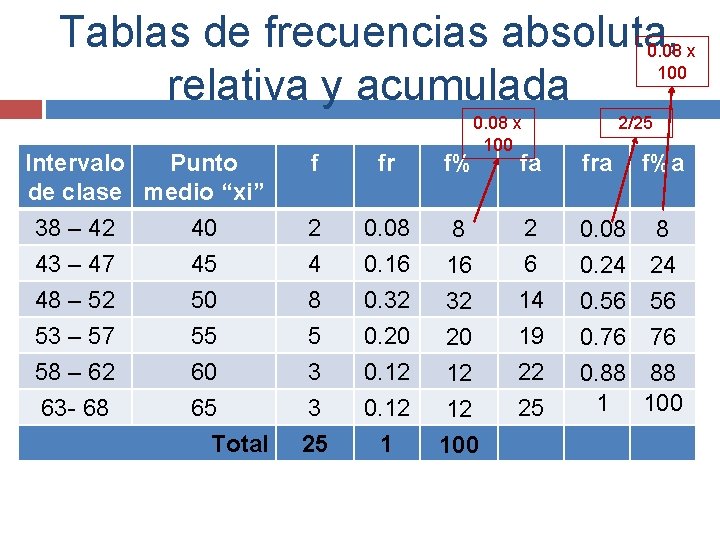
Por último se agregan las columnas: Frecuencia porcentual, “f%” ó “%f”, se obtiene multiplicando la frecuencia relativa “fr” x 100. Frecuencia relativa acumulada “fra”, se obtiene sumando las frecuencias relativas anteriores a un dato dado. Frecuencia porcentual acumulada, “f%a”, se obtiene sumando las frecuencias porcentuales acumuladas a un dato dado.

Tablas de frecuencias absoluta, 0. 08 x 100 relativa y acumulada Intervalo Punto de clase medio “xi” 38 – 42 40 43 – 47 45 48 – 52 50 53 – 57 55 58 – 62 60 63 - 68 65 Total 0. 08 x 100 2/25 f fr f% fa fra 2 4 8 5 3 3 25 0. 08 0. 16 0. 32 0. 20 0. 12 1 8 16 32 20 12 2 6 14 19 22 25 0. 08 8 0. 24 24 0. 56 56 0. 76 76 0. 88 88 1 100 12 100 f%a

Gráfica de Datos Existen dos tipos de gráficas mas usuales: Polígono de Frecuencias Histograma Otros gráficos: Gráfica de barras Pictograma Gráfico Circular o de pastel.

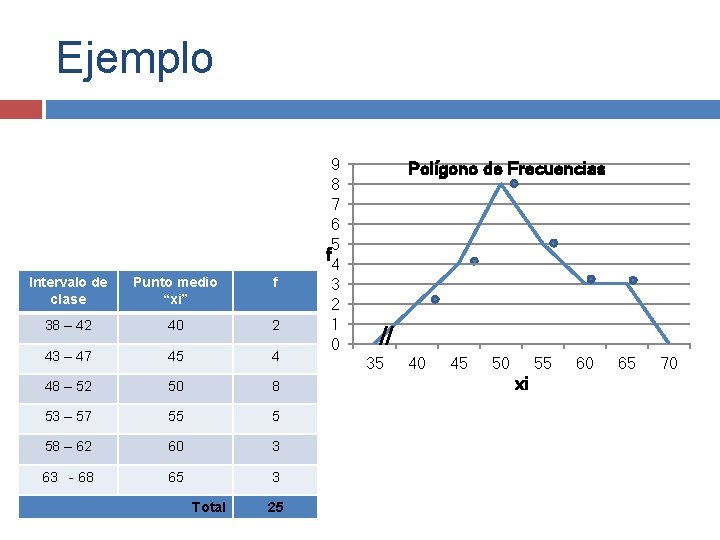
Polígono de Frecuencias Es la representación mediante un gráfico de línea. En él se muestra la distribución de frecuencias y está formado por segmentos de línea que unen los puntos correspondientes a la frecuencia de cada una de las clases. El eje “x” representa el dato “xi” y el eje “y” las frecuencias.

Ejemplo Intervalo de clase Punto medio “xi” f 38 – 42 40 2 43 – 47 45 4 48 – 52 50 8 53 – 57 55 5 58 – 62 60 3 63 - 68 65 3 Total 25 9 8 7 6 5 f 4 3 2 1 0 Polígono de Frecuencias 35 40 45 50 55 xi 60 65 70

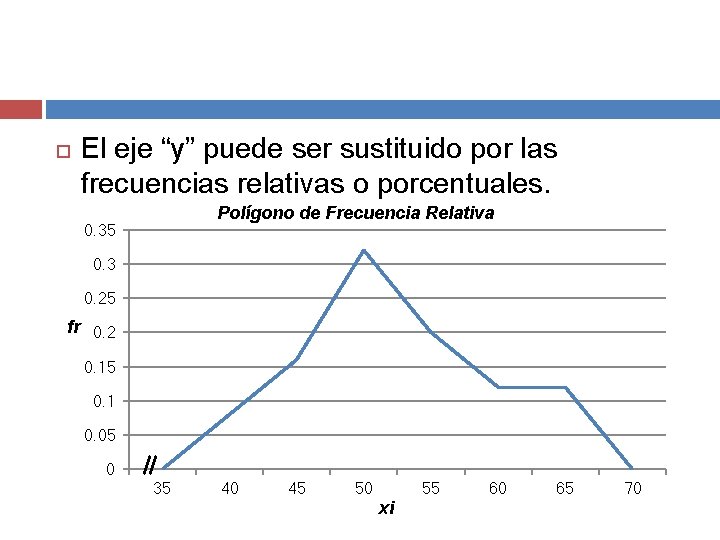
El eje “y” puede ser sustituido por las frecuencias relativas o porcentuales. Polígono de Frecuencia Relativa 0. 35 0. 3 0. 25 fr 0. 2 0. 15 0. 1 0. 05 0 35 40 45 50 xi 55 60 65 70

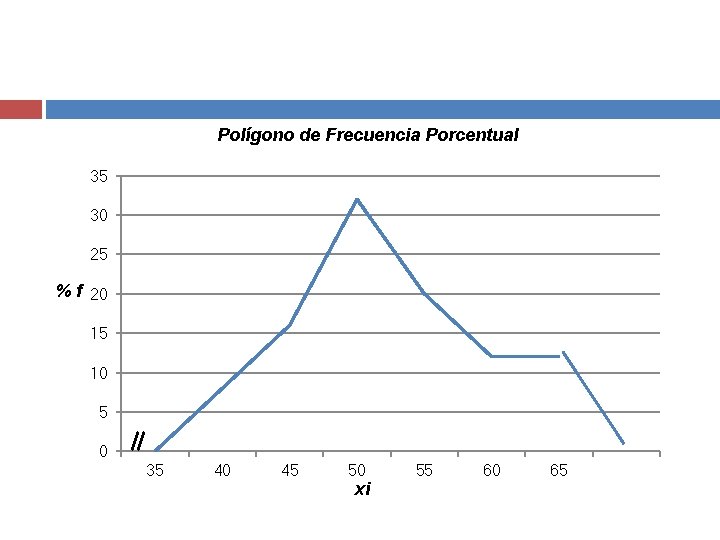
Polígono de Frecuencia Porcentual 35 30 25 % f 20 15 10 5 0 35 40 45 50 xi 55 60 65

Histograma Es la representación gráfica de los datos mediante una sucesión de rectángulos. Está formado por rectángulos cuya anchura representa a cada uno de los intervalos y la altura corresponde a la frecuencia. En el eje “x” estarán los límites verdaderos, los puntos medios y en el eje “y” las frecuencias.

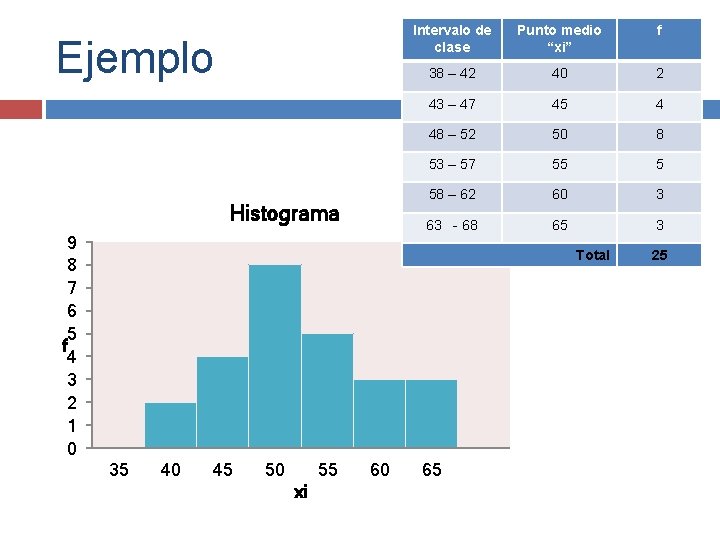
Ejemplo Histograma 9 8 7 6 5 f 4 3 2 1 0 Intervalo de clase Punto medio “xi” f 38 – 42 40 2 43 – 47 45 4 48 – 52 50 8 53 – 57 55 5 58 – 62 60 3 63 - 68 65 3 Total 35 40 45 50 55 xi 60 65 25

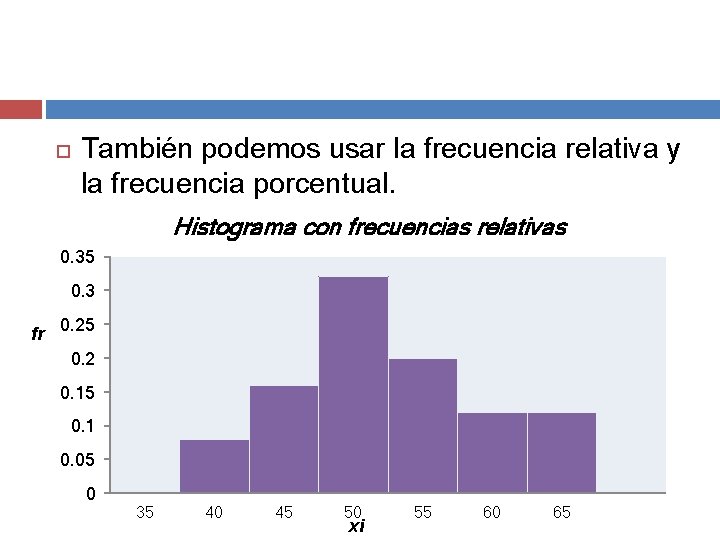
También podemos usar la frecuencia relativa y la frecuencia porcentual. Histograma con frecuencias relativas 0. 35 0. 3 fr 0. 25 0. 2 0. 15 0. 1 0. 05 0 35 40 45 50 xi 55 60 65

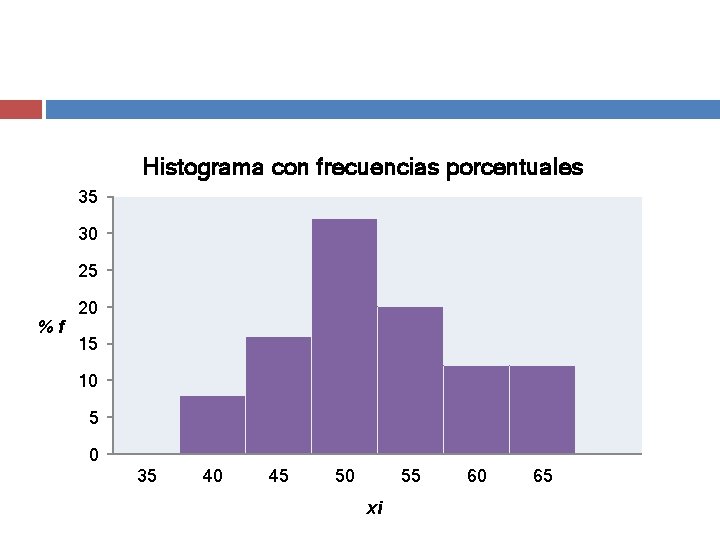
Histograma con frecuencias porcentuales 35 30 25 %f 20 15 10 5 0 35 40 45 50 55 xi 60 65

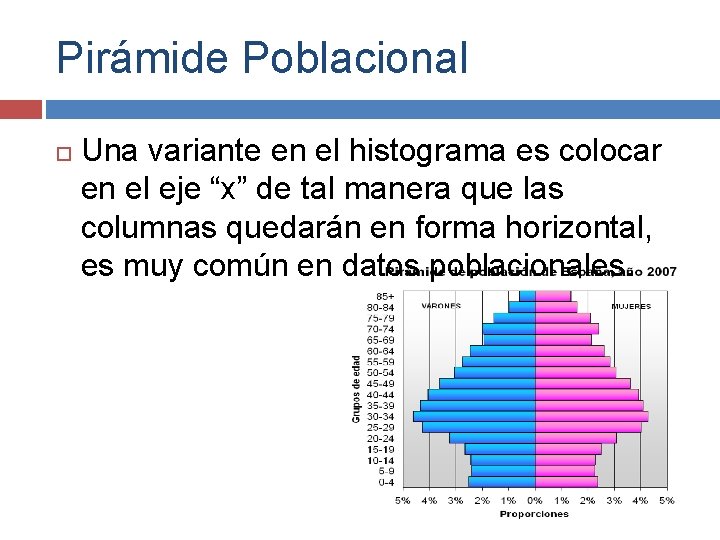
Pirámide Poblacional Una variante en el histograma es colocar en el eje “x” de tal manera que las columnas quedarán en forma horizontal, es muy común en datos poblacionales.

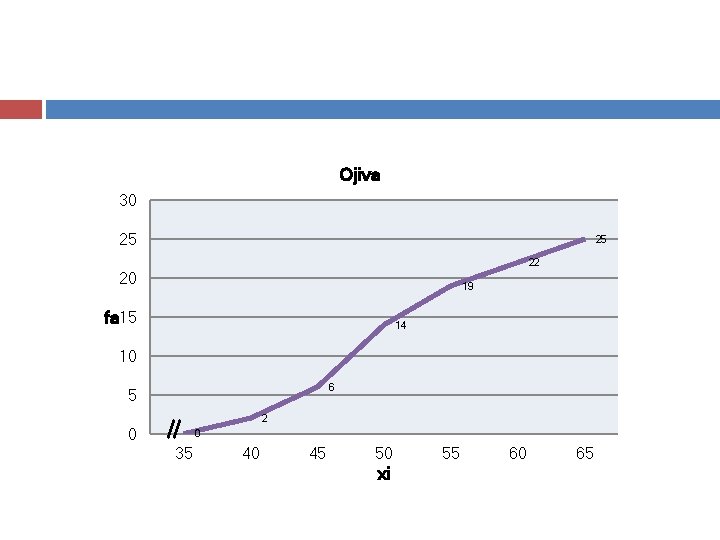
Ojiva Es la representación gráfica de las frecuencias acumuladas mediante un gráfico de línea. Se muestra la distribución de frecuencias acumuladas de los datos. En el eje “x” estarán los puntos medios y en el eje “y” las frecuencias acumuladas.

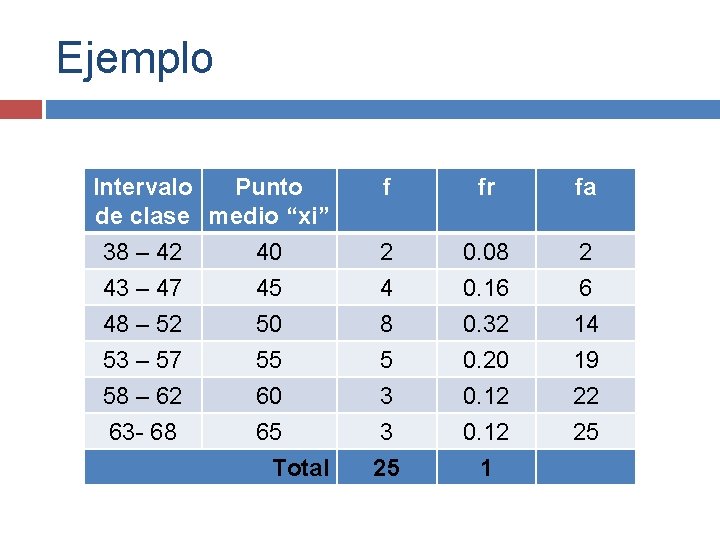
Ejemplo Intervalo Punto de clase medio “xi” 38 – 42 40 43 – 47 45 48 – 52 50 53 – 57 55 58 – 62 60 63 - 68 65 Total f fr fa 2 4 8 5 3 3 25 0. 08 0. 16 0. 32 0. 20 0. 12 1 2 6 14 19 22 25

Ojiva 30 25 25 22 20 19 fa 15 14 10 6 5 2 0 0 35 40 45 50 xi 55 60 65

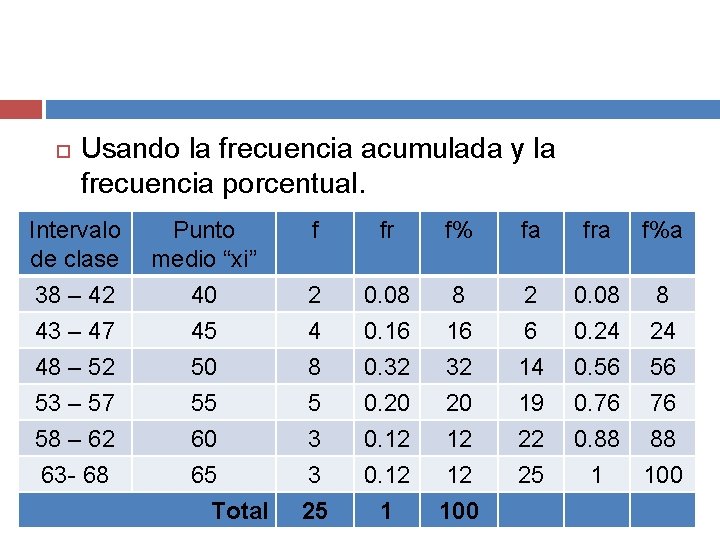
Usando la frecuencia acumulada y la frecuencia porcentual. Intervalo de clase 38 – 42 43 – 47 48 – 52 53 – 57 58 – 62 63 - 68 Punto medio “xi” 40 45 50 55 60 65 Total f fr f% fa 2 4 8 5 3 3 0. 08 0. 16 0. 32 0. 20 0. 12 8 16 32 20 12 12 2 6 14 19 22 25 25 1 100 fra f%a 0. 08 8 0. 24 24 0. 56 56 0. 76 76 0. 88 88 1 100

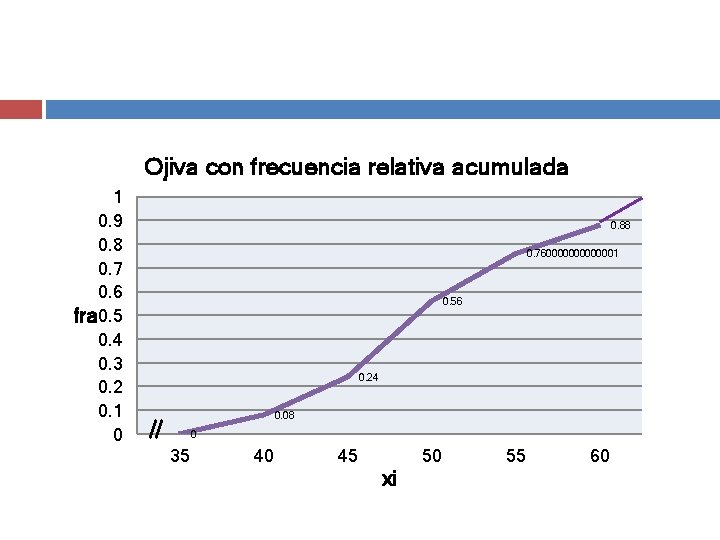
Ojiva con frecuencia relativa acumulada 1 0. 9 0. 8 0. 7 0. 6 fra 0. 5 0. 4 0. 3 0. 2 0. 1 0 0. 88 0. 760000001 0. 56 0. 24 0. 08 0 35 40 45 50 xi 55 60

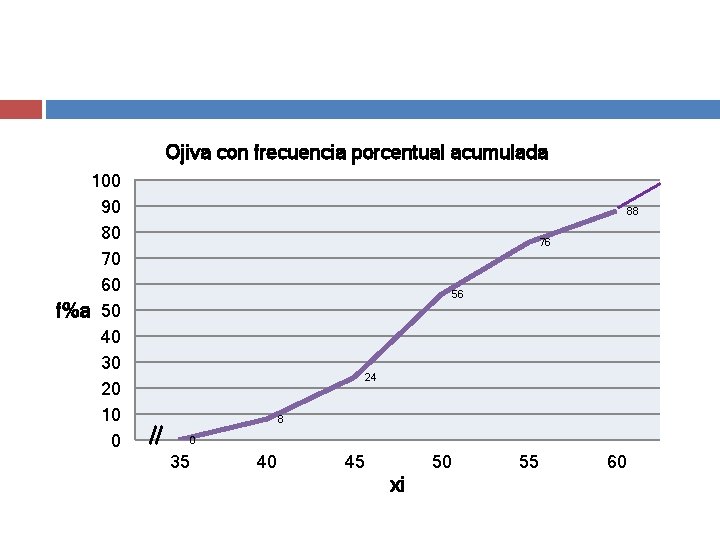
Ojiva con frecuencia porcentual acumulada 100 90 80 70 60 f%a 50 40 30 20 10 0 88 76 56 24 8 0 35 40 45 50 xi 55 60

Gráfico Circular También es llamado gráfico de pastel. Sólo se representan datos de frecuencias relativas o frecuencias porcentuales. Se debe dividir el área del círculo de manera proporcional a las frecuencias.

Agregaremos una columna a nuestra tabla de frecuencias “Frecuencia relativa al círculo”, multiplicando (fr)(360°), para mostrar la parte proporcional de círculo medida en grados que corresponde a cada intervalo.

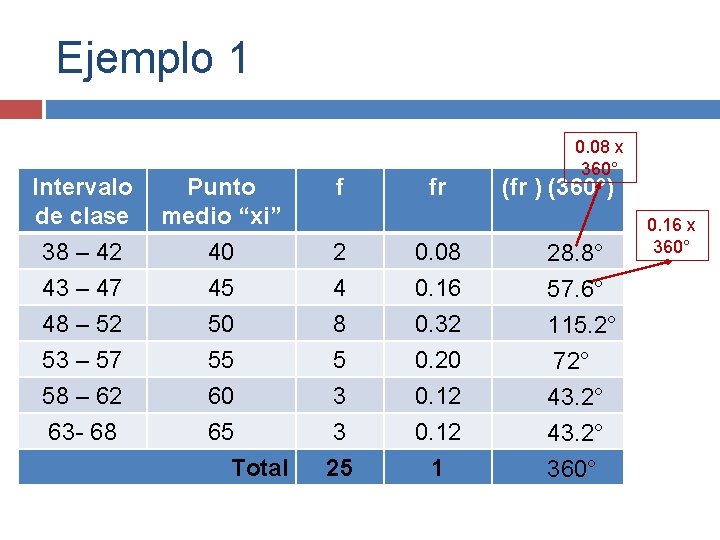
Ejemplo 1 Intervalo de clase 38 – 42 43 – 47 48 – 52 53 – 57 58 – 62 63 - 68 Punto medio “xi” 40 45 50 55 60 65 Total f 2 4 8 5 3 3 25 fr 0. 08 0. 16 0. 32 0. 20 0. 12 1 0. 08 x 360° (fr ) (360°) 28. 8° 57. 6° 115. 2° 72° 43. 2° 360° 0. 16 x 360°

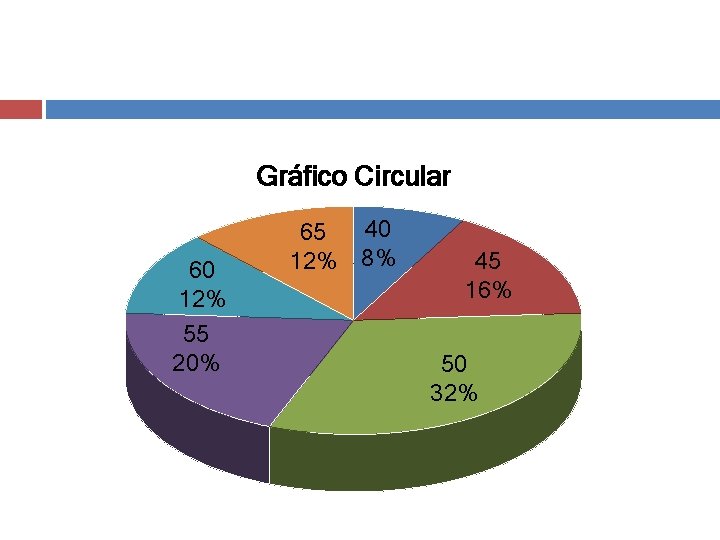
Gráfico Circular 60 12% 55 20% 40 65 12% 8% 45 16% 50 32%

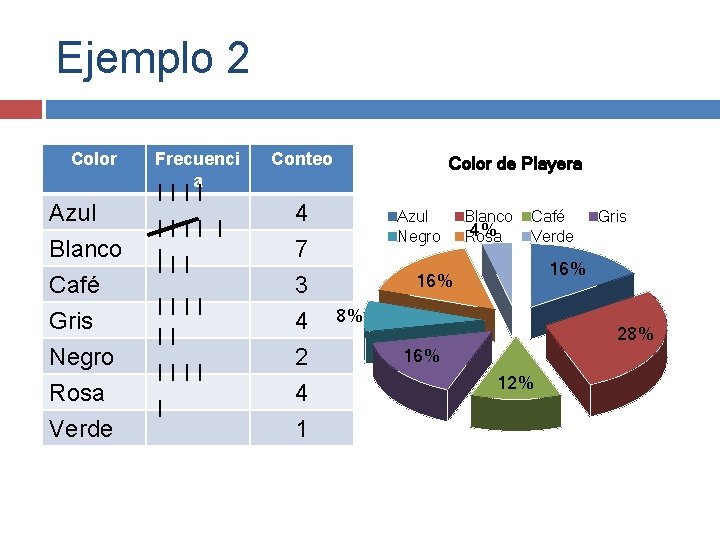
Ejemplo 2 Color Azul Blanco Café Gris Negro Rosa Verde Frecuenci a IIII I I IIII I Conteo Color de Playera 4 Azul Negro 7 2 4 1 Café Verde Gris 16% 3 4 Blanco 4% Rosa 8% 28% 16% 12%

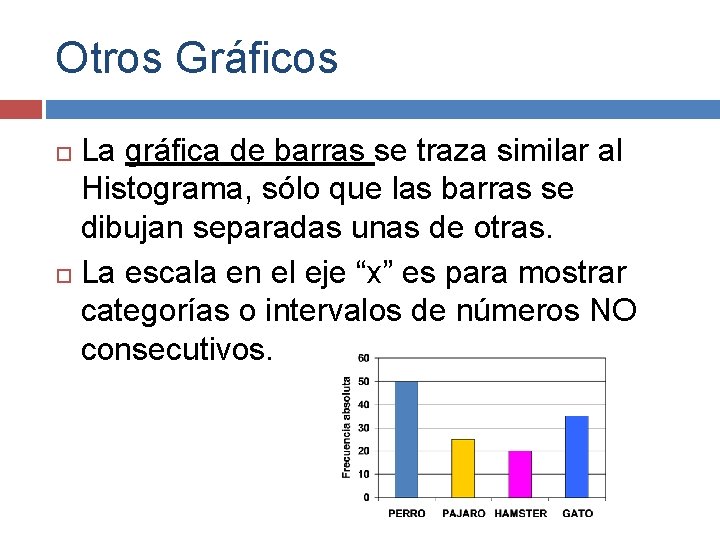
Otros Gráficos La gráfica de barras se traza similar al Histograma, sólo que las barras se dibujan separadas unas de otras. La escala en el eje “x” es para mostrar categorías o intervalos de números NO consecutivos.

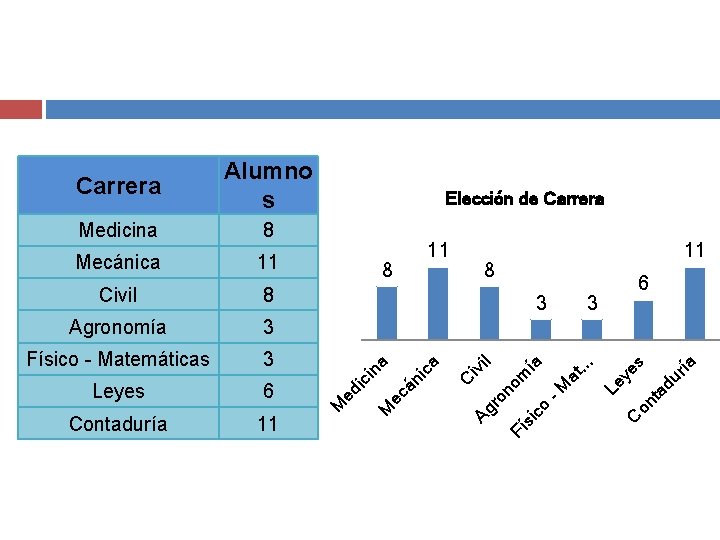
6 ye C s on ta du ría -M Le . 3 at. . ía 11 co Contaduría m 6 si Leyes Fí 3 on o Físico - Matemáticas Ag r 3 8 C iv il Agronomía 11 3 ca 8 11 ec án i Civil 8 na 11 M Mecánica ci 8 ed i Medicina Elección de Carrera M Carrera Alumno s

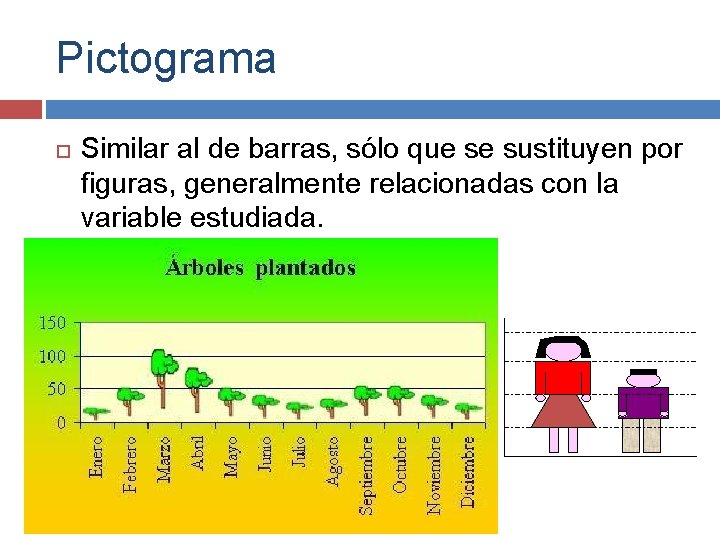
Pictograma Similar al de barras, sólo que se sustituyen por figuras, generalmente relacionadas con la variable estudiada.