Hypercontractive inequalities via SOS and the FranklRdl graph


![The hypercontractive inequalities • The reverse hypercontractive inequaltiy: when Not norms Corollary [MORSS 12]. The hypercontractive inequalities • The reverse hypercontractive inequaltiy: when Not norms Corollary [MORSS 12].](https://slidetodoc.com/presentation_image_h/2b87411a5eaf46693aeb54f510b5f74a/image-3.jpg)


![Previous works • Deg-4 SOS proof of 2 4 hypercon. ineq. [BBHKSZ 12] – Previous works • Deg-4 SOS proof of 2 4 hypercon. ineq. [BBHKSZ 12] –](https://slidetodoc.com/presentation_image_h/2b87411a5eaf46693aeb54f510b5f74a/image-6.jpg)















- Slides: 21

Hypercontractive inequalities via SOS, and the Frankl-Rödl graph Manuel Kauers (Johannes Kepler Universität) Ryan O’Donnell (Carnegie Mellon University) Li-Yang Tan (Columbia University) Yuan Zhou (Carnegie Mellon University)

The hypercontractive inequalities • Real functions on Boolean cube: • Noise operator: means each is -correlated with Projection to deg-k • The hypercontractive inequality: when Corollary. 2 4 hypercontractive ineq.
![The hypercontractive inequalities The reverse hypercontractive inequaltiy when Not norms Corollary MORSS 12 The hypercontractive inequalities • The reverse hypercontractive inequaltiy: when Not norms Corollary [MORSS 12].](https://slidetodoc.com/presentation_image_h/2b87411a5eaf46693aeb54f510b5f74a/image-3.jpg)
The hypercontractive inequalities • The reverse hypercontractive inequaltiy: when Not norms Corollary [MORSS 12]. when we have

The hypercontractive inequalities • The hypercontractive inequality: when Applications: KKL theorem, Invariance Principle • The reverse hypercontractive inequaltiy: when Applications: hardness of approximation, quantitative social choice

The sum-of-squares (SOS) proof system • Closely related to the Lasserre hierarchy [BBHKSZ 12, OZ 13, DMN 13] – Used to prove that Lasserre succeeds on specific instances • In degree-d SOS proof system To show a polynomial , write where each has degree at most d
![Previous works Deg4 SOS proof of 2 4 hypercon ineq BBHKSZ 12 Previous works • Deg-4 SOS proof of 2 4 hypercon. ineq. [BBHKSZ 12] –](https://slidetodoc.com/presentation_image_h/2b87411a5eaf46693aeb54f510b5f74a/image-6.jpg)
Previous works • Deg-4 SOS proof of 2 4 hypercon. ineq. [BBHKSZ 12] – Level-2 Lasserre succeeds on known Unique. Games instances • Constant-deg SOS proof of KKL theorem [OZ 13] – Level-O(1) Lasserre succeeds on the Balanced. Separator instances by [DKSV 06] • Constant-deg SOS proof of “ 2/π-theorem” [OZ 13] and Majority-Is-Stablest theorem [DMN 13] – Level-O(1) Lasserre succeeds on Max. Cut instances by [KV 05, KS 09, RS 09]

Results in this work • Deg-q SOS proof of the hypercon. ineq. when p=2, q=2 s for we have • Deg-4 k SOS proof of reverse hypercon. ineq. when q= for we have f f^(2 k) g g^(2 k)

Application of the reverse hypercon. ineq. to the Lasserre SDP • Frankl-Rödl graphs • 3 -Coloring – [FR 87, GMPT 11] – SDPs by Kleinberg-Goemans fails to certify [KMS 98, KG 98, Cha 02] – Arora and Ge [AG 11]: level-poly(n) Lasserre SDP certifies – Our SOS proof: level-2 Lasserre SDP certifies

Application of the reverse hypercon. ineq. to the Lasserre SDP • Frankl-Rödl graphs • Vertex. Cover – when [FR 87, GMPT 11] – Level-ω(1) LS+SDP and level-6 SA+SDP fails to certify [BCGM 11] – The only known (2 -o(1)) gap instances for SDP relaxations – Our SOS proof: level-(1/γ) Lasserre SDP certifies when

Proof sketches • SOS proof of the normal hypercon. ineq. – Induction • SOS proof of the reverse hypercon. ineq. – Induction + computer-algebra-assisted induction • From reverse hypercon. ineq. to Frankl-Rödl graphs – SOS-ize the “density” variation of the Frankl-Rödl theorem due to Benabbas-Hatami-Magen [BHM 12]

SOS proof (sketch) of the reverse hypercon. ineq.

• Statement: for exists SOS proof of • Proof. Induction on n. – Base case (n = 1). For – Key challenge, will prove later.

• Statement: for exists SOS proof of • Proof. Induction on n. – Base case (n = 1). For – Induction step (n > 1). Induction on (n-1) variables

• Statement: for exists SOS proof of • Proof. Induction on n. – Base case (n = 1). For – Induction step (n > 1). Induction by base case

Proof of the base case • Assume w. l. o. g. • “Two-point ineq. ” (where • Use the following substitutions: where ):

To show SOS proof of where By the Fundamental Theorem of Algebra, a univariate polynomial is SOS if it is nonnegative. Only need to prove are nonnegative.

To show SOS proof of where Proof of Case 1. ( Case 2. ( [Zei 90, PWZ 97], : ) Straightforward. ) With the assistance of Zeilberger's alg. then its relatively easy to check

To show SOS proof of where Proof of : By convexity, enough to prove By guessing the form of a polynomial recurrence and solving via computer, Finally prove the nonnegativity by induction.

Summary of the proof • Induction on the number of variables • Base case: “two-point” inequality – Variable substitution – Prove the nonnegativity of a class of univariate polynomials • Via the assistance of computer-algebra algorithms, find out proper closed form or recursions • Prove directly or by induction

Open questions • Is there constant-degree SOS proof for when ? Recall that we showed a (1/γ)-degree proof when.

Thanks!
 Via negativa
Via negativa Via crucis y via lucis
Via crucis y via lucis Vis lucis
Vis lucis Haz cortico nuclear
Haz cortico nuclear Palavras convergentes
Palavras convergentes Solving linear inequalities worksheet
Solving linear inequalities worksheet Quadratic inequality shading
Quadratic inequality shading Koji tsuda
Koji tsuda Solving and graphing inequalities on a number line
Solving and graphing inequalities on a number line 6-6 systems of linear inequalities
6-6 systems of linear inequalities Quadratic inequality graph
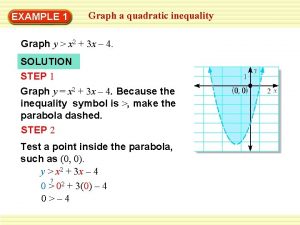
Quadratic inequality graph How do you know where to shade in a quadratic inequality
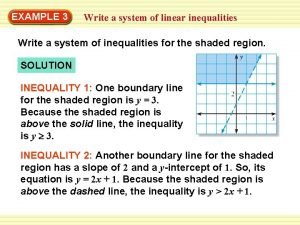
How do you know where to shade in a quadratic inequality Write a system of inequalities for the shaded region
Write a system of inequalities for the shaded region Wait-for graph
Wait-for graph Sos kinderdorf 1210 wien
Sos kinderdorf 1210 wien Title sos
Title sos Sos village multan
Sos village multan Sos order
Sos order Signs of safety model dansk
Signs of safety model dansk Sos mathematics
Sos mathematics Sos mathematics
Sos mathematics Dudesti-pantelimon 42
Dudesti-pantelimon 42