6 7 Graphing and Solving Quadratic Inequalities Objectives

+ 6 -7 Graphing and Solving Quadratic Inequalities Objectives: The student will be able to…. 1) graph Quadratic Inequalities in Two Variables. 2) solve Quadratic Inequalities in One Variable.

+ Recall how to Graph Linear Inequalities:

+ Graphing Quadratic Inequalities n You can graph quadratic inequalities in two variables using the same techniques you used to graph linear inequalities in two variables. Steps: 1) Determine whether the boundary should be solid or dashed. Graph the quadratic function.

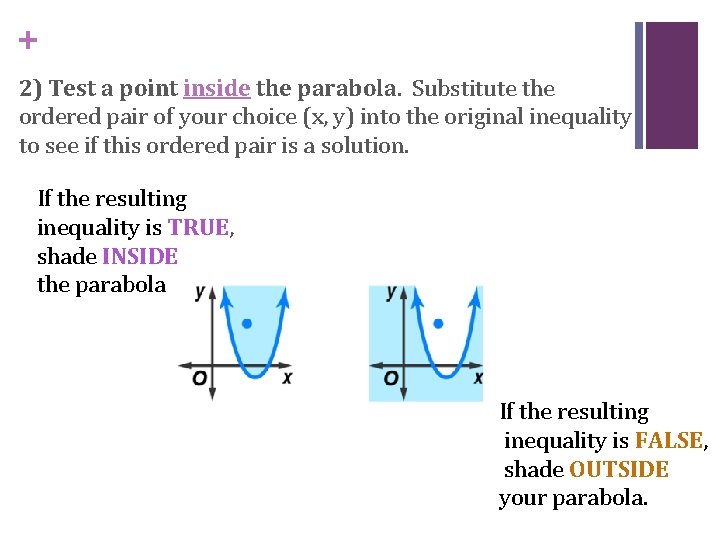
+ 2) Test a point inside the parabola. Substitute the ordered pair of your choice (x, y) into the original inequality to see if this ordered pair is a solution. If the resulting inequality is TRUE, shade INSIDE the parabola. If the resulting inequality is FALSE, shade OUTSIDE your parabola.

+ Example 1: Graph a Quadratic Inequality Recall: What different methods can we use to graph?

+ Example 2: Graph a Quadratic Inequality

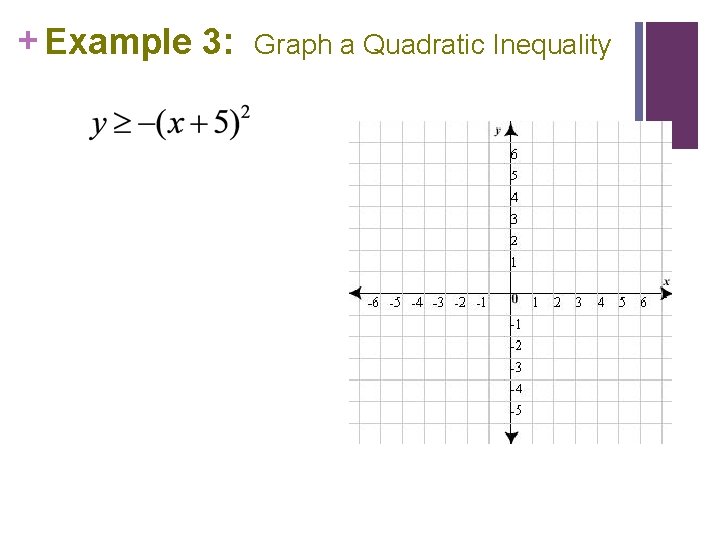
+ Example 3: Graph a Quadratic Inequality

Solving Quadratic Inequalities + n To solve a quadratic inequality in one variable, we need to analyze the graph of the related quadratic function.

+ Steps to Solving Quadratic Inequalities: n Always start by graphing n If the original inequality was of the form Identify the x values for which the graph lies BELOW the x-axis. n If the original inequality was of the form Identify the x values for which the graph lies ABOVE the x-axis. n For < or > , include the x-intercepts in the solution.

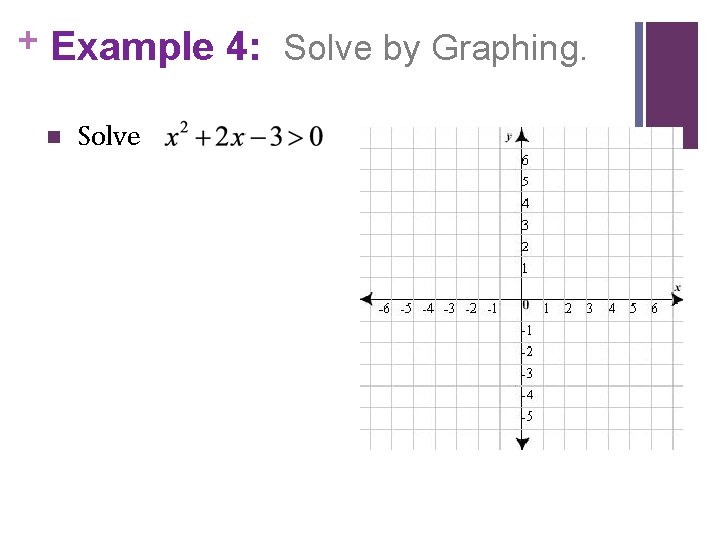
+ Example 4: Solve by Graphing. n Solve

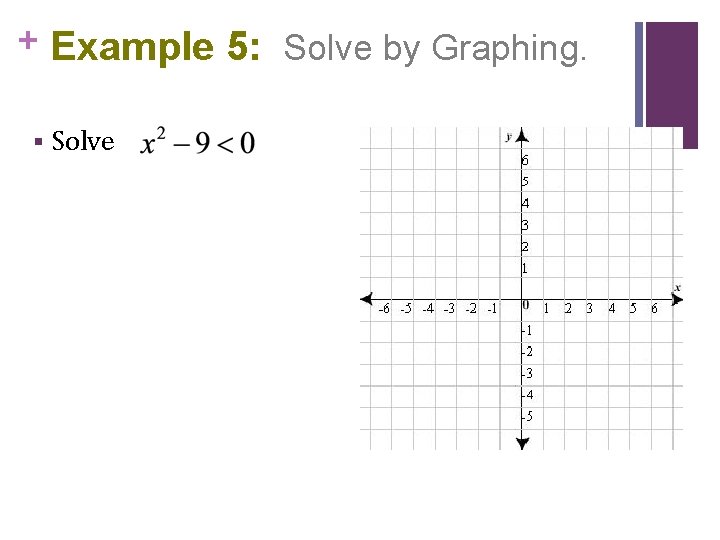
+ Example 5: Solve by Graphing. § Solve

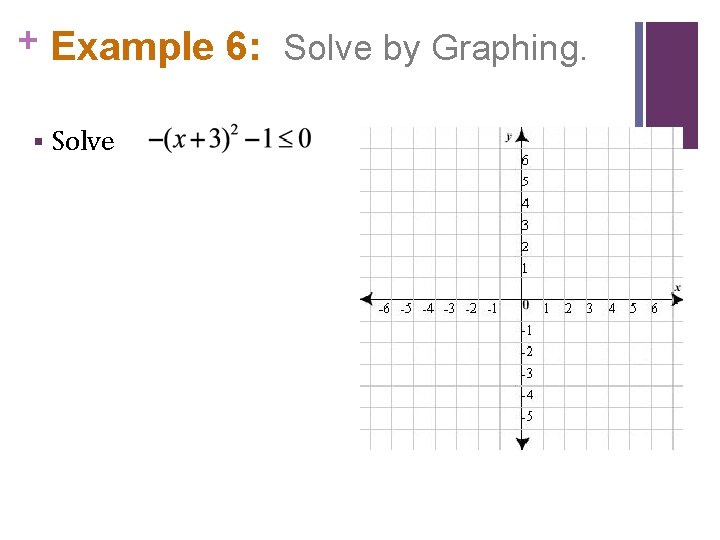
+ Example 6: Solve by Graphing. § Solve

+ Example 7: Solve by Graphing. § Solve

+ Scavenger Hunt! n Choose a partner. n Find a graph of a quadratic inequality around the room. n Start with the problem on the bottom of the paper. You may use your calculator to help you graph. n Interpret whether you are solving or graphing the inequality. n Each partner must write down the problem on their own sheet of paper. Work together to graph/solve the given inequality. n Search around the room for a graph/solution that matches yours! n Once you find it, move on to the next problem (located below the graph/solution you just found).