Humanberufliche Schulen Standorte und Schultypen im HUM Bereich

HLW Weinhartstraße, Innsbruck HLW Technikerstraße, Innsbruck HLW Reutte HLW Landeck HLW Kufstein HLW Lienz FW Pfaffenhofen FW Wörgl + AL HLT Zell HLT St. Johann in Tirol HLT Villa Blanka Tourismus Kolleg TFS Lienz KBA Falkstraße BBA Haspingerstraße, Innsbruck KBA Zams ISOP Stams BSPA, Innsbruck Schule für Sozialbetreuungsberufe SONSTIGE BSPA Kolleg - Medien Kolleg – Kndergart. BBA – 5 Jahre Kolleg - T 4 Sem. HFS – 3 Jahre TF – 3 Jahre HLT – 5 Jahre AL – Touris. 3 J. AL – 3 Jahre FW - 3 Jahre Standort HLW - 5 Jahre Schultyp

Anforderungen an Lehrpersonen in Angewandter Mathematik an BHS

Anforderungen • Planung • Methoden • Materialien • Beurteilung • Fortbildung

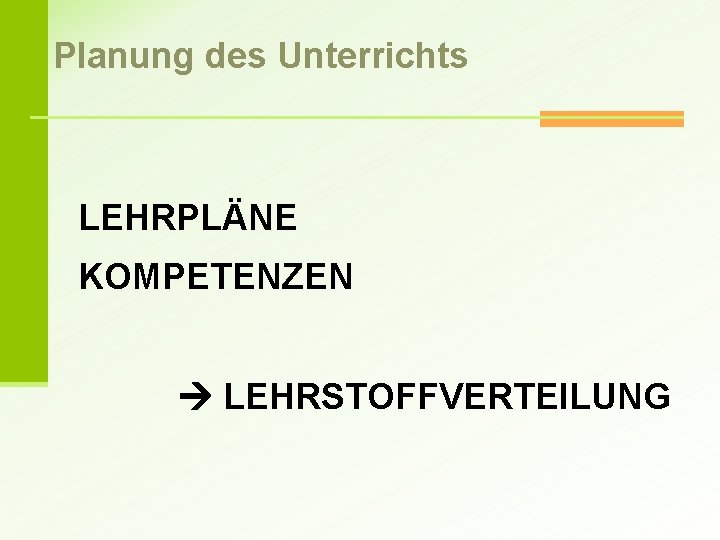
Planung des Unterrichts LEHRPLÄNE KOMPETENZEN LEHRSTOFFVERTEILUNG

Planung des Unterrichts - LEHRPLAN § ALLGEMEINES BILDUNGSZIEL § ALLGEMEINE DIDAKTISCHE GRUNDSÄTZE § UNTERRICHTSPRINZIPIEN § BILDUNGS- und LEHRAUFGABE

Planung des Unterrichts - LEHRPLAN Bildungs- und Lehraufgabe: Die Schülerinnen und Schüler können im Bereich „Analysis“ n Grenzwert und Stetigkeit von Funktionen auf der Basis eines intuitiven Begriffsverständnisses argumentieren, n die Begriffe Differenzenquotient (mittlere Änderungsrate) und Differentialquotient („momentane“ Änderungsrate) als Änderungsraten interpretieren und zur Lösung von Aufgaben einsetzen n den Zusammenhang zwischen Funktion und Ableitungsfunktion erklären, n Ableitungen modellieren, berechnen, interpretieren und argumentieren

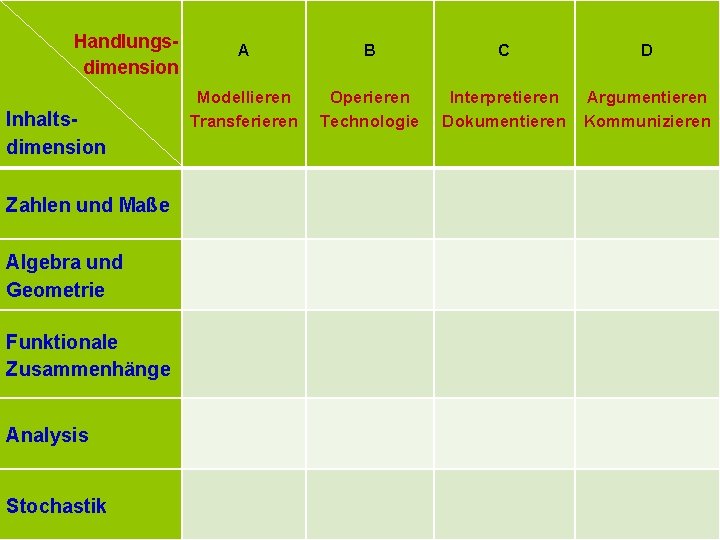
Handlungsdimension Inhaltsdimension Zahlen und Maße Algebra und Geometrie Funktionale Zusammenhänge Analysis Stochastik A B C D Modellieren Transferieren Operieren Technologie Interpretieren Dokumentieren Argumentieren Kommunizieren

Grundkompetenzen-Katalog

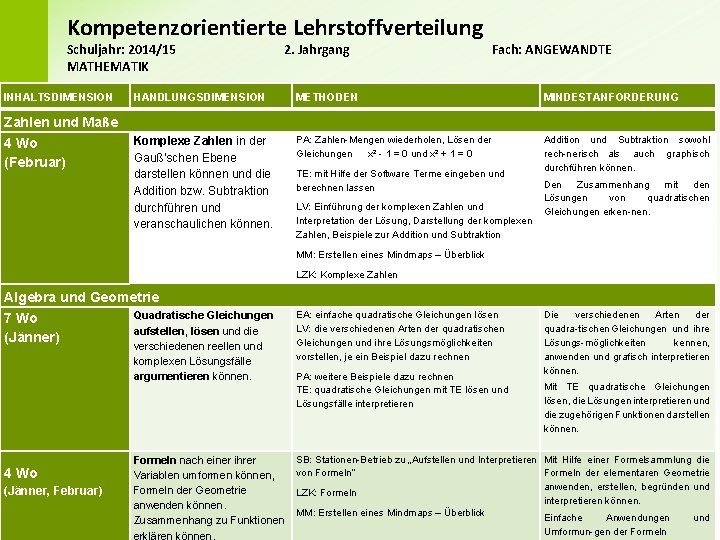
Kompetenzorientierte Lehrstoffverteilung Schuljahr: 2014/15 MATHEMATIK INHALTSDIMENSION 2. Jahrgang Fach: ANGEWANDTE HANDLUNGSDIMENSION METHODEN MINDESTANFORDERUNG Komplexe Zahlen in der Gauß’schen Ebene darstellen können und die Addition bzw. Subtraktion durchführen und veranschaulichen können. PA: Zahlen Mengen wiederholen, Lösen der Gleichungen x² 1 = 0 und x² + 1 = 0 Addition und Subtraktion sowohl rech nerisch als auch graphisch durchführen können. Zahlen und Maße 4 Wo (Februar) TE: mit Hilfe der Software Terme eingeben und berechnen lassen LV: Einführung der komplexen Zahlen und Interpretation der Lösung, Darstellung der komplexen Zahlen, Beispiele zur Addition und Subtraktion Den Zusammenhang mit den Lösungen von quadratischen Gleichungen erken nen. MM: Erstellen eines Mindmaps – Überblick LZK: Komplexe Zahlen Algebra und Geometrie 7 Wo (Jänner) 4 Wo (Jänner, Februar) Quadratische Gleichungen aufstellen, lösen und die verschiedenen reellen und komplexen Lösungsfälle argumentieren können. EA: einfache quadratische Gleichungen lösen LV: die verschiedenen Arten der quadratischen Gleichungen und ihre Lösungsmöglichkeiten vorstellen, je ein Beispiel dazu rechnen Formeln nach einer ihrer Variablen umformen können, Formeln der Geometrie anwenden können. Zusammenhang zu Funktionen erklären können. SB: Stationen Betrieb zu „Aufstellen und Interpretieren Mit Hilfe einer Formelsammlung die von Formeln“ Formeln der elementaren Geometrie anwenden, erstellen, begründen und LZK: Formeln interpretieren können. MM: Erstellen eines Mindmaps – Überblick Einfache Anwendungen und PA: weitere Beispiele dazu rechnen TE: quadratische Gleichungen mit TE lösen und Lösungsfälle interpretieren Die verschiedenen Arten der quadra tischen Gleichungen und ihre Lösungs möglichkeiten kennen, anwenden und grafisch interpretieren können. Mit TE quadratische Gleichungen lösen, die Lösungen interpretieren und die zugehörigen Funktionen darstellen können. Umformun gen der Formeln

Anforderungen • Planung • Methoden • Materialien • Beurteilung • Fortbildung

Methoden für den Unterricht Stationenbetrieb, Arbeitsauftrag, Expertenpuzzle, Partnerarbeit, Lehrervortrag, Eigenverantwortliches Lernen, … Cool - Cooperatives Offenes Lernen

Methoden für den Unterricht n nicht jeder Inhalt kann mit derselben Methode n nicht jede Lehrperson kann einen Inhalt mit derselben Methode vermitteln n nicht jede Methode eignet sich gleich gut für die eine Klasse wie für die andere n nicht jeder Schüler/jede Schülerin kann mit derselben Methode n…

• Fachkompetenz • Methodenkompetenz • Soziale Kompetenz • Personale Kompetenz • Kommunikative Kompetenz • Emotionale Kompetenz

Anforderungen • Planung • Methoden • Materialien • Beurteilung • Fortbildung

Bücher • Welches Buch entscheidet das Fachkollegium • Kompetenzorientierte Bücher Informieren Sie sich jetzt schon über die verschiedenen Bücher und auch Formelsammlungen

Technologie • Entscheidung des Fachkollegiums • in Technologie einarbeiten Informieren Sie sich jetzt schon über die verschiedenen Technologien! GTR über CAS Rechner bis zu Computerprogrammen wie Geo. Gebra, Mathcad, Maple, Wolfram Alpha, Mathematica

Technologie Mindestanforderung für s. RDP an BHS § Darstellung von Funktionsgraphen § Möglichkeiten des numerischen Lösens von Gleichungen und Gleichungssystemen § Numerisches Integrieren § Grundlegende Funktionen der Matrizenrechnung § Funktionen für statistische Kenngrößen, lineare Regression und Korrelation, Binomial und Normalverteilung

Materialien für den Unterricht Was bringt die Zukunft? Technologie am Tablet, Interaktive Bücher, …

Anforderungen • Planung • Methoden • Materialien • Beurteilung • Fortbildung

Beurteilung Welche Kompetenzen sollten die Schüler und Schülerinnen haben? Welche sollten Sie benoten?

Kompetenz …. auf die Sichtweise kommt es an

Beurteilung LBVO Leistungsbeurteilungsverordnung • Punkte • Prozente • Verbales Beurteilungsraster

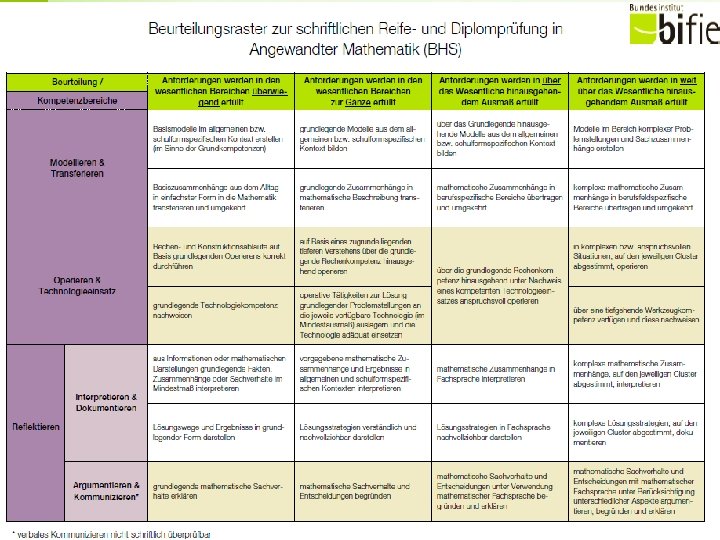
Anforderungen • Planung • Methoden • Materialien • Beurteilung • Fortbildung

Fortbildung Bereitschaft zur Weiterbildung • zu den Unterrichtsmethoden • Technologie • Zusatzfächer • Neuerungen • …

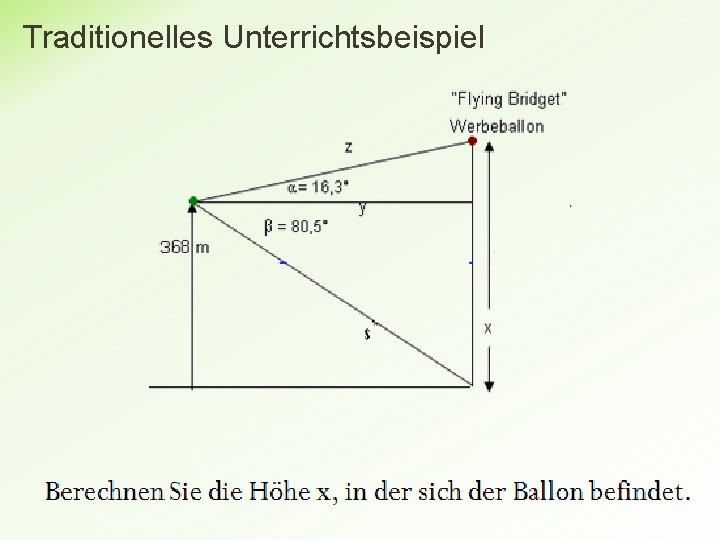
Traditionelles Unterrichtsbeispiel

Kompetenzorientierte Aufgabe a) Interpretieren Sie die Grafik und finden Sie einen passenden Angabetext, aus dem diese Skizze entwickelt werden kann. b) Berechnen Sie die Flughöhe x des Ballons in Metern (m). c) Der Ballon steigt vom Startplatz aus mit einer durchschnitt lichen Geschwindigkeit von 2, 3 Metern pro Sekunde (m/s) senkrecht nach oben. Stellen Sie die Funktion, die Höhe in Abhängigkeit von der Zeit beschreibt, grafisch dar. Lesen Sie die Höhe ab, die der Ballon nach einer halben Stunde erreicht.

Kompetenzorientierte Aufgaben http: //aufgabenpool. bifie. at/bhs/index. php? action=14

Vielen Dank für Ihre Aufmerksamkeit

TIPP Wählen Sie eine Schulstufe, organisieren Sie sich den Lehrplan und ein entsprechendes Buch von einer Schulform und erstellen Sie für ein Jahr eine Lehrstoffverteilung.

Planung des Unterrichts Lehrpläne Bisher https: //www. bmbf. gv. at/schulen/unterricht/lp/lp_bbs. html http: //www. abc. berufsbildendeschulen. at/de/dlcollection. asp Oberstufe Neu https: //www. bmbf. gv. at/schulen/unterricht/ba/oberstufeneu. html Kompetenzenkataloge https: //www. bifie. at/node/1390

Hilfreiche Links Lehrpläne: https: //www. bmbf. gv. at/schulen/unterricht/lp/lp_bbs. html Bifie: http: //www. bifie. at/node/81 Kompetenzenkataloge: https: //www. bifie. at/node/1390 Bifie Aufgabenpool für Übungsklausuraufgaben: http: //aufgabenpool. bifie. at/bhs/index. php? action=14 HUM: Bundesarge WEB http: //teaching. eduhi. at/Mam/bundesarge/index. htm Aufgabenpool der HUM Bundes ARGE http: //teaching. eduhi. at/Mam/aufgabenpool. BIST/index. htm