HOMOMORFISMA Definisi Suatu pemetaan dari grup G kedalam

HOMOMORFISMA Definisi Suatu pemetaan dari grup G kedalam grup G’ dikatakan homomorfisma jika untuk setiap a, b G, (ab)= (a) (b).

CONTOH (x)=e untuk setiap x G, demikian juga 1. 2. (x)=x untuk setiap x G merupakan homomorfisma. Misalkan G grup dari semua bilangan real terhadap operasi penjumlahan (catatan ab menjadi a+b) dan G’ adalah grup dari semua bilangan real tak nol dengan operasi perkalian. Definiskan : G G’ dengan (a)=2 a untuk setiap a G. adalah homomorfisma dari G kedalam G’.

CONTOH 3. Misalkan G=S 3={e, , , 2 } dan G’ = {e, }. Definisikan pemetaan f: G G’ dengan f( j i)= i, maka f(e)=e, f( )=e, f( 2)=e, f( )= , f( 2 )= .

CONTOH 4. Misalkan G grup dari bilangan bulat dibawa operasi penjumlahan dan G=G’. Untuk setiap x G definisikan dengan (x)=2 x. Maka adalah homomorfisma. 5. Misalkan G grup dari bilangan real tak nol dibawa operasi perkalian. G’={1, -1} dimana 1. 1=1, (-1)=1, (1)1=1(-1)=-1. Definisikan : G G’ dengan (x)=1 jika x bilangan positif, (x)=-1 jika x negatif.

CONTOH 6. Misalkan G grup bilangan bulat dibawa operasi penjumlahan, misalkan G’ adalah grup bilangan bulat modulo n dibawa operasi penjumlahan. Definisikan dengan (x) = sisa dari x dibagi n. Maka adalah homomorfisma. 7. Misalkan G grup dari bilangan real positif dibawa operasi perkalian dan G’ adalah grup dari semua bilangan real dibawa operasi penjumlahan. Definisikan : G G’ dengan (x) = log 10(x). Maka (xy) = log 10(x)+log 10(y) = (x)+ (y).

CONTOH 8. Misalkan G grup dari matriks bilangan real 2 x 2, dengan ad-bc 0 dibawah operasi perkalian matriks. Misalkan G’ grup dari semua bilangan real tak nol dibawa operasi perkalian. Definisikan : G G’ dengan. Tunjukan bahwa adalah homomorfisma grup.

LEMMA Misalkan G grup, N subgrup normal dari G; definisikan pemetaan dari G ke G/N dengan (x)=Nx untuk setiap x G. Maka adalah homomorfisma dari G pada G/N

DEFINISI Jika adalah suatu homomorfisma dari G kedalam G’, dengan kernel dari , K , adalah didefinisikan dengan K ={x G: (x)=e’, dimana e’ adalah unsur identitas dari G’}.

LEMMA 1. Jika adalah suatu homomorfisma dari G 2. 3. kedalam G’, maka: a. (e) = e’, dimana e’ adalah unsur identitas dari G’. b. (x-1)= (x )-1 untuk setiap x G. Jika adalah suatu homomorfisma dari G kedalam G’ dengan kernel K, maka K adalah subgrup normal dari G. Jika adalah suatu homomorfisma dari G pada G’ dengan kernel K, maka himpunan semua bayangan invers dari g’ G’ dibawa dalam G adalah Kx, dimana x adalah bayangan invers dari g’ dalam G.

DEFINISI 1. 2. Suatu homomorfisma dari G kedalam G’ dikatakan isomorfisma jika satu-satu. Dua grup G, G* adalah isomorfik jika terdapat suatu isomorfisma dari G pada G*. Dalam hal ini dinotasikan G G*.

CATATAN 1. 2. 3. G G Jika G G * maka G* G. Jika G G*, G* G** maka G G**

AKIBAT Suatu homomorfisma dari G kedalam G’ dengan kernel K adalah isomorfisma dari G dalam G’ jika dan hanya jika K =(e).

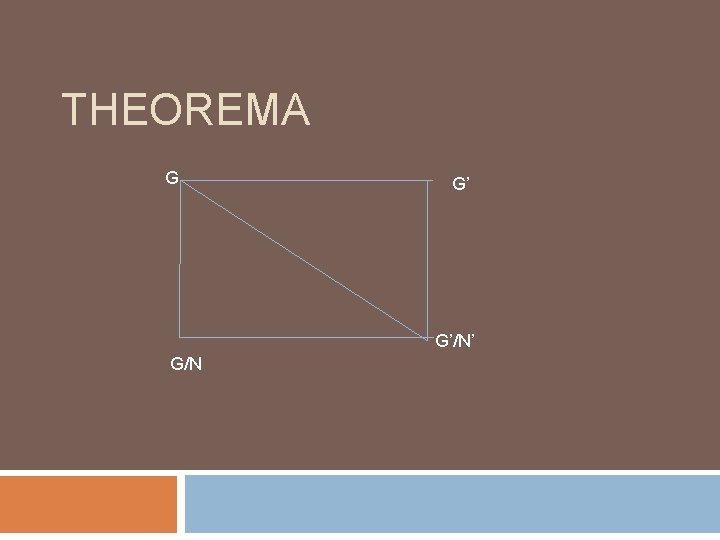
TEOREMA Misalkan homomorfisma dari G pada G’ dengan kernel K. Maka G/K G’.

LEMMA Misalkan homomorfisma dari G pada G’ dengan kernel K. Untuk H’ subgrup dari G’. Misalkan H didefinisikan dengan H={x G: (x) H’}. Maka H adalah subgrup dari G dan H K; Jika H’ adalah normal dalam G’, maka H adalah normal dalam G.

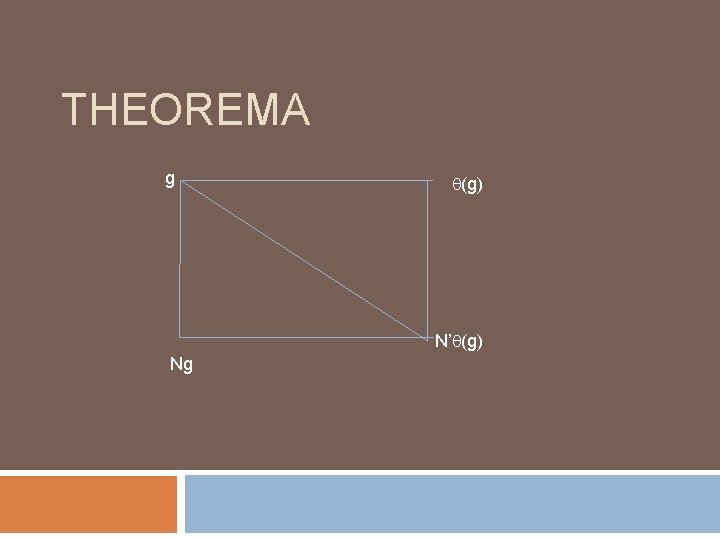
THEOREMA Misalkan homomorfisma dari G pada G’ dengan kernel K. Dan Misalkan N’ subgrup normal dari G’, N={x G: (x) N’}. Maka G/N (G’/N’). Ekivalen mengatakan G/N (G/K)/(N/K)

THEOREMA G G’ G’/N’ G/N

THEOREMA g (g) N’ (g) Ng