Homework 3 is posted due on June 26






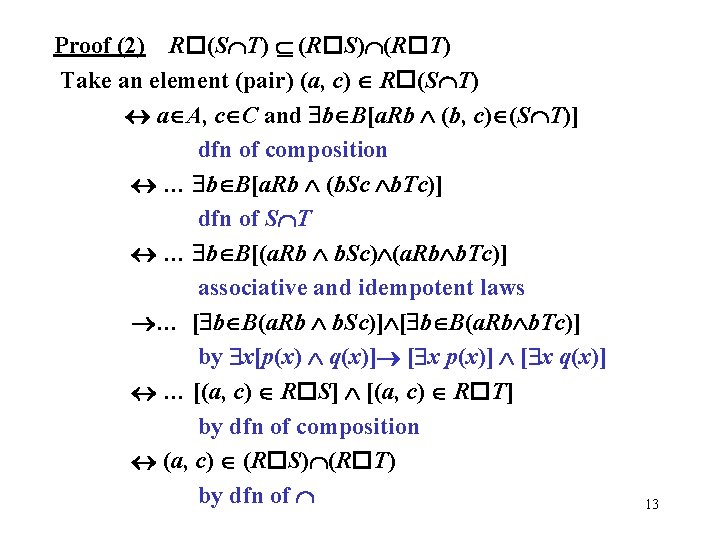










- Slides: 31

Homework #3 is posted (due on June 26) Today’s topics: • Associative and distributive properties of composition • Powers of a relation • Inverse relation 1

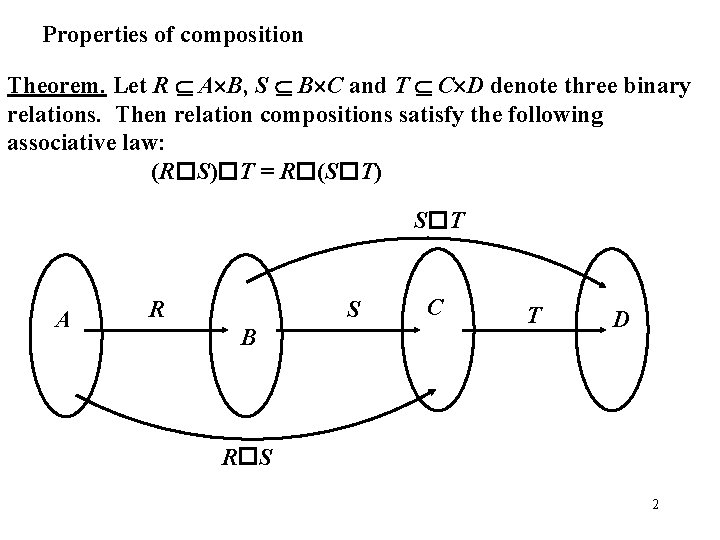
Properties of composition Theorem. Let R A B, S B C and T C D denote three binary relations. Then relation compositions satisfy the following associative law: (R S) T = R (S T) S T A R S B C T D R S 2

Theorem. Let R A B, S B C and T C D denote three binary relations. Then relation compositions satisfy the following associative law: (R S) T = R (S T) Proof. First note that both sides define a relation from A to D. We also note the following: (R S) T = {(a, d) | a A and d D and c C [(a, c) R S c. Td ]} (by the definition of composition T ) = {(a, d) |… ( c C, b B) [(a. Rb b. Sc ) c. Td ]} (by definition of R S ) = {(a, d) |… ( c C, b B) [a. Rb (b. Sc c. Td )]} (by associative property of ) = {(a, d) |… ( b B) [a. Rb (b, d ) S T ]} (by definition of S T ) = R (S T) 3 R ) (by the definition of composition

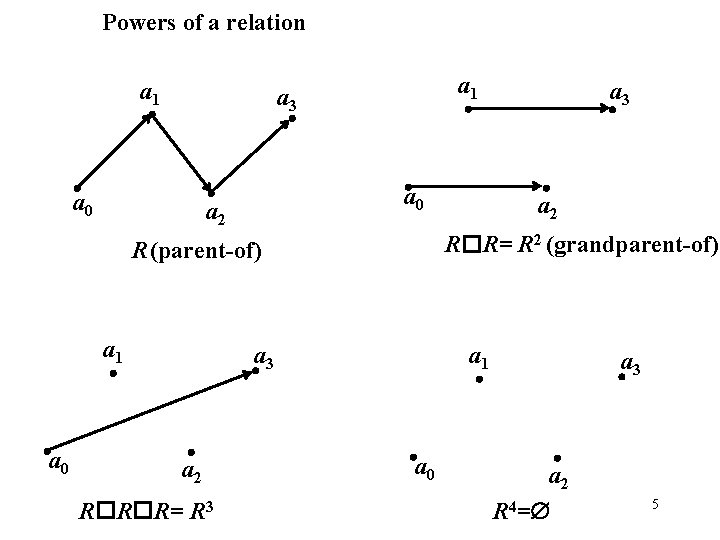
Associative property of composition means, that no ambiguity arises if we simply write R S T. We can also define powers of a relation R A A recursively as R 1=R and Rn+1=Rn R (n 1) Definition. A path in a relation R is a sequence a 0, … , ak with k 0 such that (ai, ai+1) R for every i<k. We call k the length of the path. A 1 a 0 • 7 a 2 • 5 • a 3 • 1, 5, 7, 6 – a path of length 3 1 6 • a 3 4 • 4

Powers of a relation a 1 a 3 a 0 a 3 a 0 a 2 R R R= R 3 a 2 R R= R 2 (grandparent-of) R (parent-of) a 1 a 0 a 2 a 3 a 1 a 3 a 0 a 2 R 4= 5

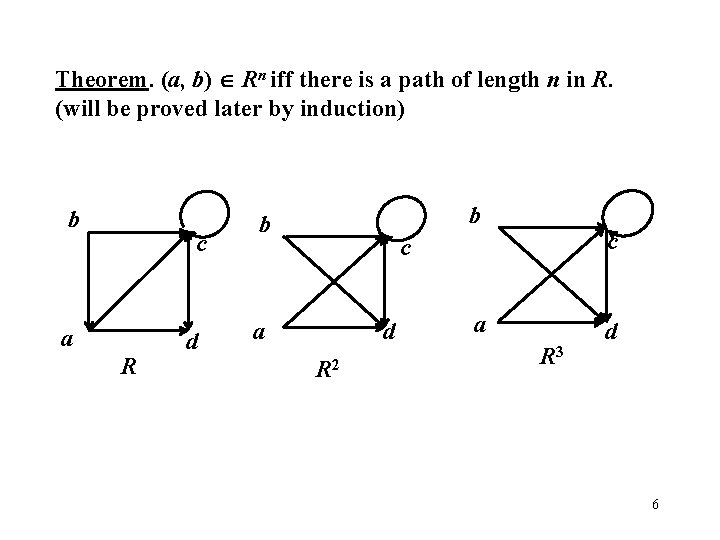
Theorem. (a, b) Rn iff there is a path of length n in R. (will be proved later by induction) b c a R d b b c c a d R 2 a R 3 d 6

Theorem. 1) If a relation R A A is reflexive, then R 2 is also reflexive 2) If a relation R A A is symmetric, then R 2 is also symmetric 3) If a relation R A A is transitive, then R 2 is also transitive. Proof 1) If R A A is reflexive, then for any a A, (a, a) R. To prove that R 2 is reflexive, we need to show that for any a A, (a, a) R 2, i. e. you can ‘return back to a in two steps’. This is obviously true, because you can simply repeat two loops. Note, that we can prove in general, that if (a, a) R, then (a, a) Rn for any n > 0 (repeat loop n times) 7

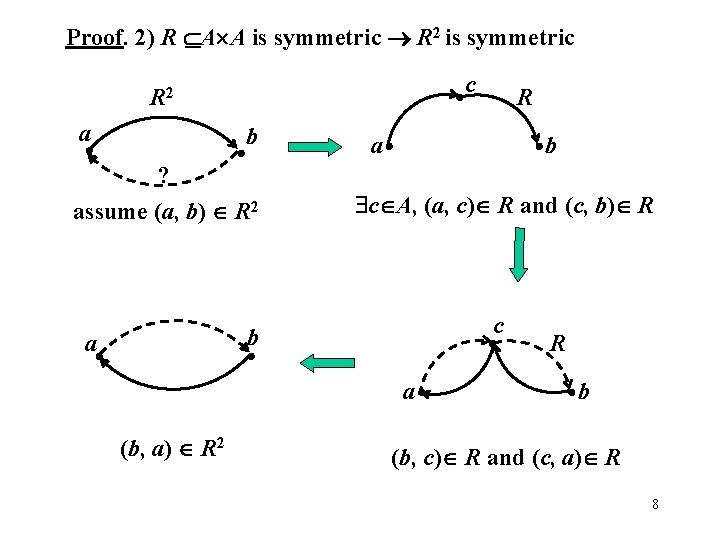
Proof. 2) R A A is symmetric R 2 is symmetric R 2 a b ? assume (a, b) R 2 b c A, (a, c) R and (c, b) R c a (b, a) R 2 R a b a c R b (b, c) R and (c, a) R 8

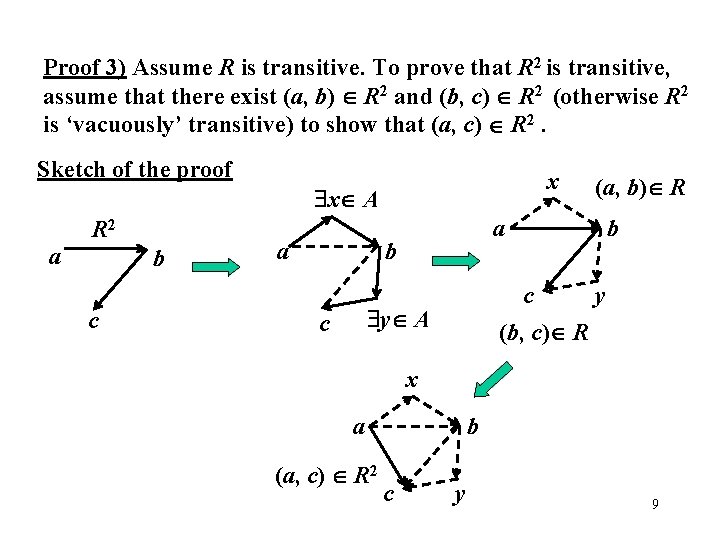
Proof 3) Assume R is transitive. To prove that R 2 is transitive, assume that there exist (a, b) R 2 and (b, c) R 2 (otherwise R 2 is ‘vacuously’ transitive) to show that (a, c) R 2. Sketch of the proof x x A R 2 a b c a a b b c y A c (a, b) R y (b, c) R x a (a, c) R 2 b c y 9

It is interesting also to see how the composition distributes over union and intersection. Theorem. Let R A B, S B C and T B C denote three binary relations. Then 1) R (S T) = (R S) (R T) 2) R (S T) (R S) (R T) 10

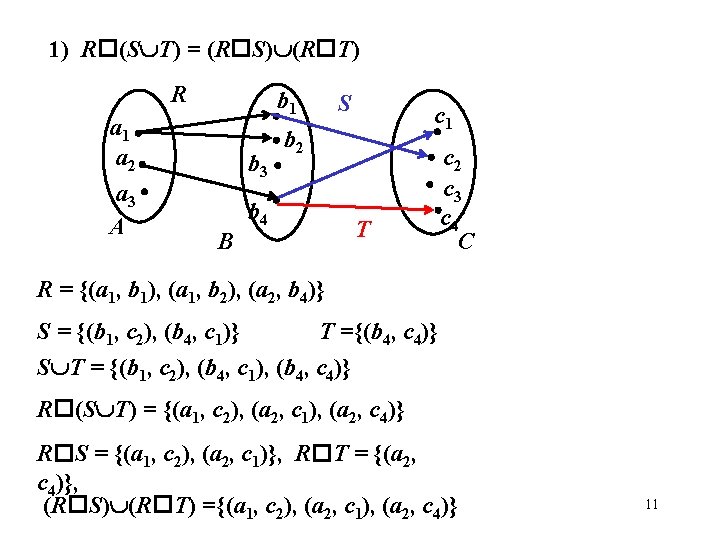
1) R (S T) = (R S) (R T) R a 1 a 2 a 3 A b 1 b 2 S c 1 B b 4 c 2 c 3 c 4 C b 3 T R = {(a 1, b 1), (a 1, b 2), (a 2, b 4)} S = {(b 1, c 2), (b 4, c 1)} T ={(b 4, c 4)} S T = {(b 1, c 2), (b 4, c 1), (b 4, c 4)} R (S T) = {(a 1, c 2), (a 2, c 1), (a 2, c 4)} R S = {(a 1, c 2), (a 2, c 1)}, R T = {(a 2, c 4)}, (R S) (R T) ={(a 1, c 2), (a 2, c 1), (a 2, c 4)} 11

Proof (1) R (S T)={(a, c)|a A and c C and b B [a. Rb (b, c) S T]}… …. . dfn of R = {(a, c)|… b B [a. Rb ( b. Sc b. T c)]}……………dfn of = {(a, c)|… b B [(a. Rb b. Sc) (a. Rb b. T c)]}……distributive law = {(a, c)|… [ b B (a. Rb b. Sc)] [ b B (a. Rb b. T c)]} by x[p(x) q(x)] [ x p(x)] [ x q(x)] = {(a, c)|… [(a, c) R S ] [(a, c) R T ]} by dfn of composition = {(a, c)|… (a, c) R S R T } by dfn of = R S R T 12
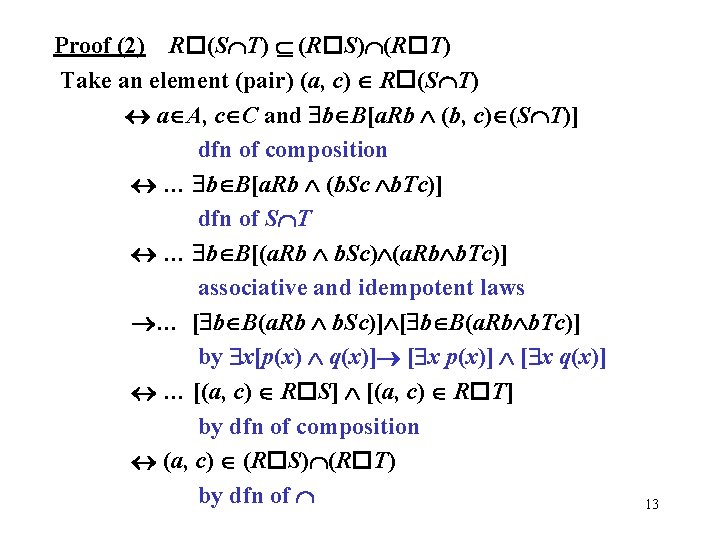
Proof (2) R (S T) (R S) (R T) Take an element (pair) (a, c) R (S T) a A, c C and b B[a. Rb (b, c) (S T)] dfn of composition … b B[a. Rb (b. Sc b. Tc)] dfn of S T … b B[(a. Rb b. Sc) (a. Rb b. Tc)] associative and idempotent laws … [ b B(a. Rb b. Sc)] [ b B(a. Rb b. Tc)] by x[p(x) q(x)] [ x p(x)] [ x q(x)] … [(a, c) R S] [(a, c) R T] by dfn of composition (a, c) (R S) (R T) by dfn of 13

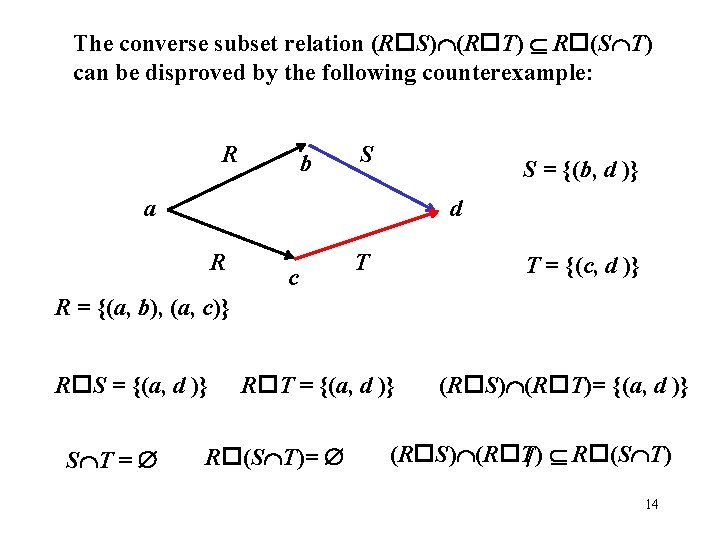
The converse subset relation (R S) (R T) R (S T) can be disproved by the following counterexample: R b S S = {(b, d )} a d R c T T = {(c, d )} R = {(a, b), (a, c)} R S = {(a, d )} S T = R T = {(a, d )} R (S T)= (R S) (R T)= {(a, d )} (R S) (R T) / R (S T) 14

Definition. Inverse of relation R is defined as: R-1 = {(a, b) | (b, a) R}. • It is just relation “turned backward”. • If R A B , then R-1 B A • Inverse of “parent-of” is “child of”. 15

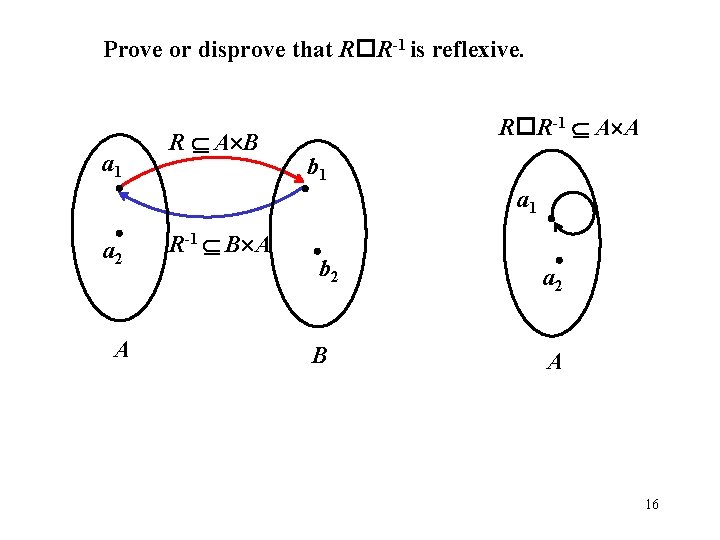
Prove or disprove that R R-1 is reflexive. a 1 R A B a 2 A R R-1 A A b 1 R-1 B A a 1 b 2 B a 2 A 16

Theorem. Let R be a binary relation from A to B and S be a binary relation from B to C, so that R S is a composite relation from A to C. Then the inverse of this relation (R S)-1 = S-1 R-1 Proof. (R S)-1 is a binary relation from C to A. (R S)-1 = {(c, a) | (a, c) R S }……. . by the definition of inverse = {(c, a) | b B, a. Rb and b. Sc}…. by dfn of composition = {(c, a) | b B, (b, a) R-1 and (c, b) S-1 } by dfn of inverse = {(c, a) | b B, (c, b) S-1 and (b, a) R-1} by commutative property of and = {(c, a) | b B, (c, a) S-1 R-1} by dfn of composition = S-1 R-1 17

Closures of relations A closure “extends” a relation to satisfy some property. But extends it as little as possible. Definition. The closure of relation R with respect to property P is the relation S that i) contains R ii) satisfies property P iii) is contained in any relation satisfying i) and ii). That is S is the “smallest” relation satisfying i) and ii). 18

Just a reminder: • reflexive: a. Ra for any a A • symmetric: a. Rb b. Ra • transitive: a. Rb b. Rc a. Rc • anti-symmetric: a. Rb b. Ra a = b, i. e. a b, a. Rb b. Ra 19

Lemma 1. The reflexive closure of R is S = R {(a, a) | a A } =r(R). Proof. In accordance to the definition of a closure, we need to prove three things to show that S is reflexive closure: i) S contains R ii) S is reflexive iii) S is the smallest relation satisfying i) and ii). S contains R and is reflexive by design. Furthermore, any relation satisfying i) must contain R, any satisfying ii) must contain the pairs (a, a), so any relation satisfying both i) and ii) must contain S 20

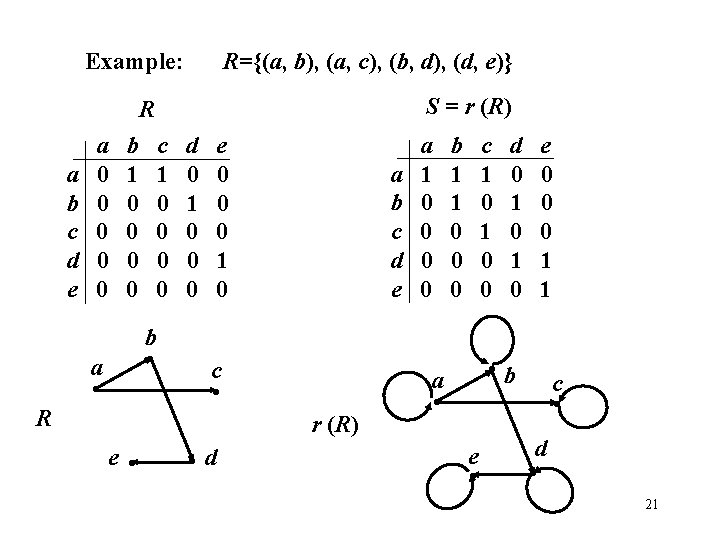
Example: R={(a, b), (a, c), (b, d), (d, e)} S = r (R) R a b c d e a 0 0 0 b 1 0 0 c 1 0 0 b • a • R d 0 1 0 0 0 e 0 0 0 1 0 a b c d e c • r (R) e • • d a 1 0 0 b 1 1 0 0 0 c 1 0 0 d 0 1 0 e 0 0 0 1 1 • b a • e • c • d • 21

Sometimes the relation on A that consists of all loops is called identity relation on A, i. e. IA={(a, a)|a A} Then reflexive closure of a relation R A A is r(R)=R IA Example of a reflexive closure. Let A be any set and consider the relation on Power(A) R = {(x, y) Power(A) | x y} The reflexive closure of R would be the relation: R IPower(A)={(x, y) Power(A)|(x, y) R or (x, y) IPower(A)} ={(x, y) Power(A)| x y or x=y} ={(x, y) Power(A)| x y} Thus, the reflexive closure of the ‘proper subset’ relation is the ‘subset’ relation. 22

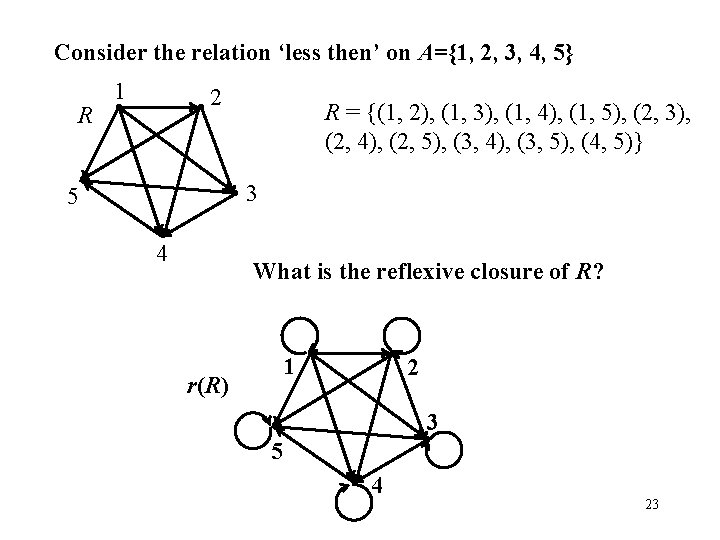
Consider the relation ‘less then’ on A={1, 2, 3, 4, 5} R 1 2 5 R = {(1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5)} 3 4 What is the reflexive closure of R? 1 r(R) 2 3 5 4 23

Lemma 2. The symmetric closure of R is S = R R-1 =s(R) Proof. S is symmetric and contains R. It is also the smallest such. For suppose we have some symmetric relation T with R T. To show that T contains S we need to show that R-1 T. Take any (a, b) R-1 , it implies (b, a) R , and (b, a) T, since R T. But then (a, b) T as well, because T is symmetric by assumption. So, S = R R-1 T. 24

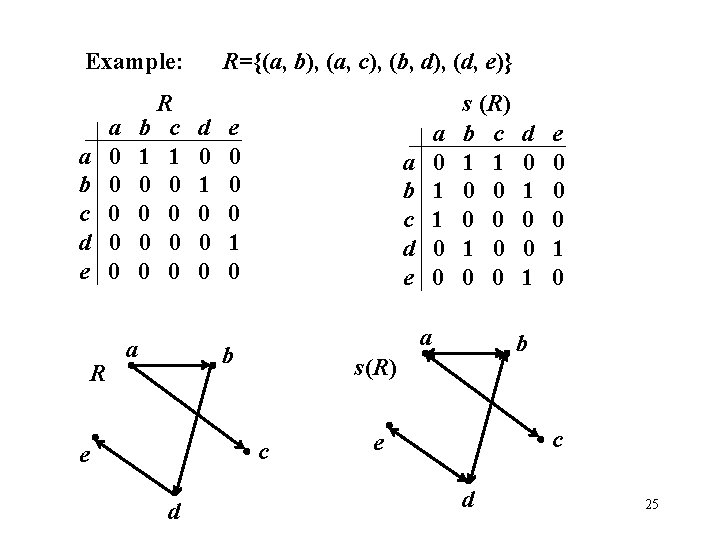
Example: R={(a, b), (a, c), (b, d), (d, e)} R b c 1 1 0 0 0 0 s (R) b c 1 1 0 0 0 a b c d e R e a 0 0 0 a d 0 1 0 0 0 e 0 0 0 1 0 a b c d e a b s(R) d a 0 1 1 0 0 c e d 0 1 0 0 1 e 0 0 0 1 0 b c d 25

Theorem. The transitive closure of a relation R is the set S = {(a, b) | there is a path from a to b in R}= t (R) Proof. Let’s show that S is transitive. Suppose (a, b) S and (b, c) S. This means there is a path from a to b and a path from b to c in R. If we “concatenate” them (attach the end of the (a, b)-path to the start of the (b, c)-path) we get a path from a to c. Thus, (a, c) S and S is transitive. We need to show, that any transitive relation T containing R contains S. Let’s prove by contradiction. Assume that there exists a transitive relation T containing R, that is smaller then S. 26

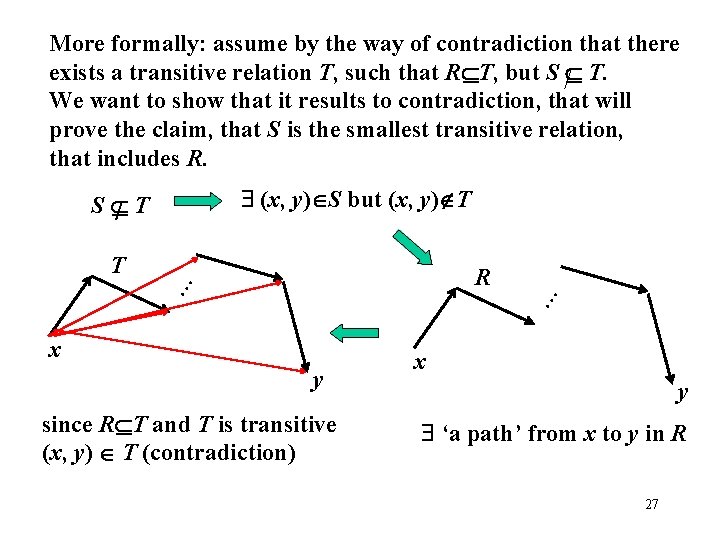
More formally: assume by the way of contradiction that there exists a transitive relation T, such that R T, but S / T. We want to show that it results to contradiction, that will prove the claim, that S is the smallest transitive relation, that includes R. (x, y) S but (x, y) T S /T T … … R x y since R T and T is transitive (x, y) T (contradiction) x y ‘a path’ from x to y in R 27

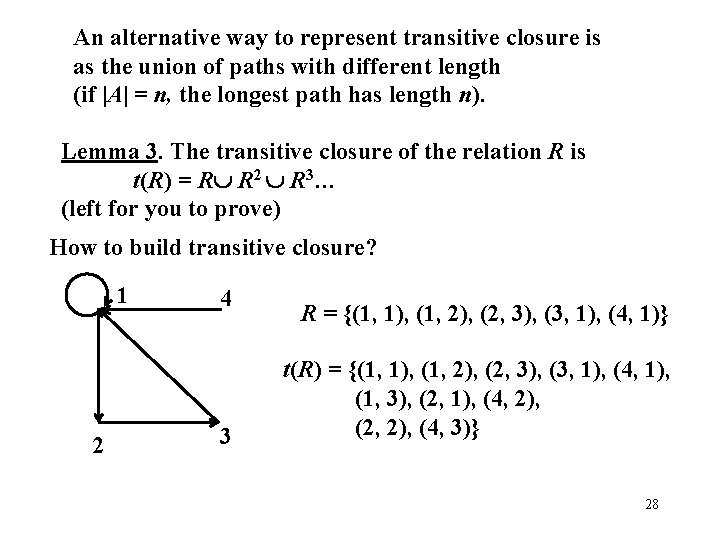
An alternative way to represent transitive closure is as the union of paths with different length (if |A| = n, the longest path has length n). Lemma 3. The transitive closure of the relation R is t(R) = R R 2 R 3… (left for you to prove) How to build transitive closure? 1 2 4 3 R = {(1, 1), (1, 2), (2, 3), (3, 1), (4, 1)} t(R) = {(1, 1), (1, 2), (2, 3), (3, 1), (4, 1), (1, 3), (2, 1), (4, 2), (2, 2), (4, 3)} 28

We can also define a composition of closures, e. g. tr(R) = t(r(R)), rs(R)=r(s(R)), etc. It turns out, that the order of composition does matter. Theorem. For any binary relation R A A st(R) ts(R). By theorem about symmetric and transitive closures st(R) = s(t(R)) = t(R) (t(R))-1 = (R R 2 R 3 …)-1 ts(R) = t(s(R)) = t(R R-1) = (R R-1)2 (R R-1)3… By the distributive property of composition over union (R R-1)2= (R R-1) = R (R R-1) R-1 (R R-1) = R R-1 R R-1 = R 2 R R-1 R R-2, where R-1= R-2 29

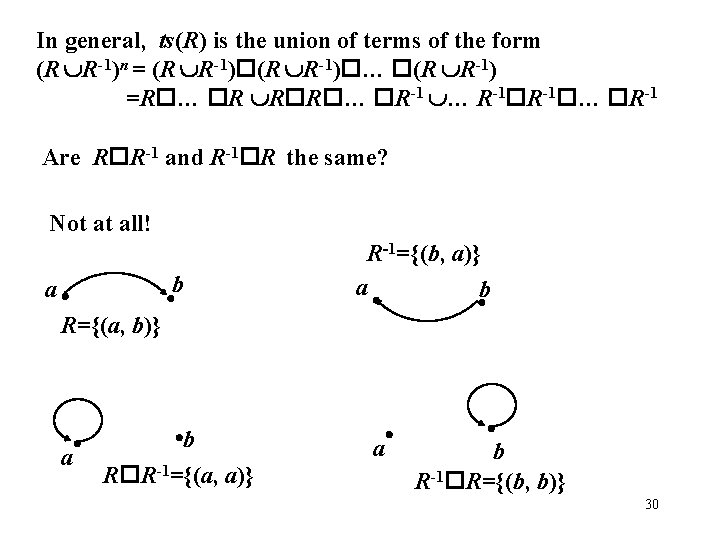
In general, ts(R) is the union of terms of the form (R R-1)n = (R R-1) … (R R-1) =R … R R R … R-1 R-1 … R-1 Are R R-1 and R-1 R the same? Not at all! b a R-1={(b, a)} a b R={(a, b)} a b R R-1={(a, a)} a b R-1 R={(b, b)} 30

We can observe, that ts(R) includes compositions of all possible sequences of R and R-1, while st(R) is a union of positive and negative powers of R (but not mixtures). So, it can be proved that st(R) ts(R), but ts(R) st(R). Proof. Take arbitrary (x, y) st(R) to show that (x, y) ts(R). By the Lemma 2 (x, y) st(R) implies that (x, y) t(R) (t(R))-1. We have two cases. Case 1: (x, y) t(R), i. e. there exists a path from x to y in R. It implies that there exist a path from x to y in s(R), since R s(R) = R R-1. By the definition of transitive closure it means that (x, y) t(s(R)). Case 2: (x, y) (t(R))-1 , i. e. (y, x) t(R), and similar to the case 1, there exists a path from y to x in R, that implies the path in s (R). It implies there exists a path from x to y, or (x, y) ts(R). Try to find a counterexample to disproves that ts(R) st(R). 31