HGSKOLEN I AGDER Agder University College Derivasjon Stigningen

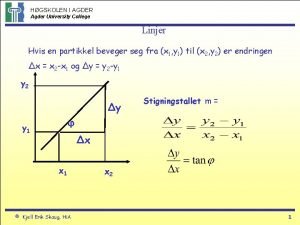
HØGSKOLEN I AGDER Agder University College Derivasjon Stigningen eller helningen til en kurve i x=x 0 er stigningstallet til tangenten i x=x 0 og er definert ved y 1=f(x 0+h) y 0=f(x 0) x 0 h x 0+h Dette er den deriverte av f(x) i x=x 0 og kalles f`(x) eller df/dx. Hvis f`(x) eksisterer er f(x) differensierbar i de punkter f`(x) eksisterer © Kjell Erik Skaug, Hi. A 1

HØGSKOLEN I AGDER Agder University College Derivasjon Notasjon: y`eller f`(x) uttales deriverte av y dy/dx, df(x)/dx uttales dydx y`|x=a er den deriverte av y for x=a Y`= dy/dx © Kjell Erik Skaug, Hi. A 2

HØGSKOLEN I AGDER Agder University College Derivasjonsregler 1. Konstant f(x)=c df/dx=0 2. Potenser f(x)=xn f(x)=x df/dx=nxn-1 df/dx=1 3. u en funksjon med x f(x)=cu df/dx=c*du/dx 4. sum u og v funksjon med x f(x) =u(x)+v(x) df/dx= du/dx+dv/dx © Kjell Erik Skaug, Hi. A 3

HØGSKOLEN I AGDER Agder University College Derivasjonsregler-2 u(x) og v(x) er funksjoner med x 5. Produktregelen f(x) = u(x)*v(x) 6. Brøkregel eller kvotientregel © Kjell Erik Skaug, Hi. A 4

HØGSKOLEN I AGDER Agder University College Derivasjon Ekpempel y=|x| er deriverbar for alle verdier av x unntatt x=0 fordi y=x når x=>0 og y`= 1 og y=-x når x<0 og y`= -1 Funksjoner er ikke deriverbar for x=0 fordi den deriverte skifter verdi i x=0. y har heller ikke tangent i punktet x=0 © Kjell Erik Skaug, Hi. A 5

HØGSKOLEN I AGDER Agder University College Derivasjon Teorem 1 Deriverbarhet - kontinuitet Hvis f har en derivert i x=c. så er f kontinuerlig i x=c Teorem 2, Mellomverditeoremet Hvis a og b er to vilkårlige punkter i et intervall hvor f er deriverbar, så vil f`derivert ha alle verdier mellom f`(a) og f`(b) © Kjell Erik Skaug, Hi. A 6

HØGSKOLEN I AGDER Agder University College 2. 2 Derivert som endring Gjennomsnittelig endring av f mellom f(x 0) og f(x 0+h) er når punktet x 0 får et tilegg h (h=x 1 -x 0) y 1=f(x 0+h) y 0=f(x 0) x 0 Hvor raskt f endres i punktet x=x 0 er den deriverte av f i punktet x 0, nemlig © Kjell Erik Skaug, Hi. A h x 0+h 7

HØGSKOLEN I AGDER Agder University College Bruk av derivasjon Ex 1: Arealet av en sirkel med diameter D er A=( /4)D 2. Hvor raskt endres arealet mhp D når D er 10 m? d. A/d. D= ( /4)*2 D = ( /2)*D når D=10 m blir endringen d. A/d. D= ( /2)*10= 5 m 2/m. Posisjon, hastighet, akselerasjon Hvis posisjonen s(t) endres med tiden som s=f(t) er Hastighet (velocity) lik v(t)=ds/dt Fart (speed) er |v(t)|=|ds/dt! Akselerasjon: a(t)=dv/dt=d 2 s/dt 2 © Kjell Erik Skaug, Hi. A 8

HØGSKOLEN I AGDER Agder University College Økonomi - Produksjon av ulike enheter c(x) er kostnader for å produsere x enheter Marginale kostnader er hvor mye kostnadene endres når det er produsert x enheter Gjennomsnittskostnad for å produsere h stk ekstra fra x stk er Marginale kostnader er kan også brukes tilnærmet for å lage en ekstra enhet Revenue inntekter behandles tilsvarende © Kjell Erik Skaug, Hi. A 9

HØGSKOLEN I AGDER Agder University College Derivasjon- trigonometriske funksjoner f(x) = sin x df/dx = cos x f(x) = cos x df/dx = -sin x f(x) = tan x df/dx = 1/cos 2 x © Kjell Erik Skaug, Hi. A 10

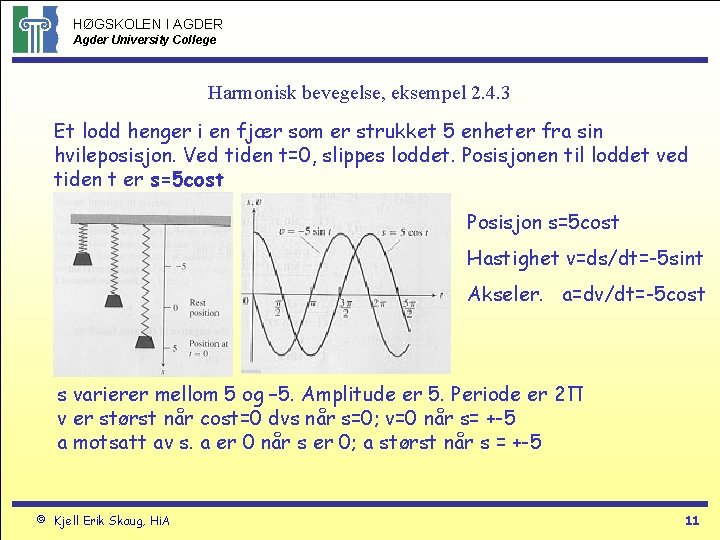
HØGSKOLEN I AGDER Agder University College Harmonisk bevegelse, eksempel 2. 4. 3 Et lodd henger i en fjær som er strukket 5 enheter fra sin hvileposisjon. Ved tiden t=0, slippes loddet. Posisjonen til loddet ved tiden t er s=5 cost Posisjon s=5 cost Hastighet v=ds/dt=-5 sint Akseler. a=dv/dt=-5 cost s varierer mellom 5 og – 5. Amplitude er 5. Periode er 2Π v er størst når cost=0 dvs når s=0; v=0 når s= +-5 a motsatt av s. a er 0 når s er 0; a størst når s = +-5 © Kjell Erik Skaug, Hi. A 11

HØGSKOLEN I AGDER Agder University College Kjederegelen Den deriverte av en sammensatt funksjon f(g(x)) er den deriverte av f(g(x)) ganger deriverte av g(x) eller Hvis f(u) er deriverbar i punktene u=g(x) og g(x) er deriverbar i x vil den sammensatte funksjonen f(g(x)) = f o g(x) være deriverbar i x og være df(g(x))/dx = f`(g(x))*g`(x) eller hvis y=f(u) og u=g(x) så er © Kjell Erik Skaug, Hi. A 12

HØGSKOLEN I AGDER Agder University College Eksempler Eksempel 2 y=(3 x 2+1)2 =9 x 4+6 x 2+1 y`er I y`= 36 x 3 + 12 x eller II y=u 2 og u= 3 x 2+1 y`= dy/du*du/dx= 2 u(6 x) y`= 2(3 x 2+1)6 x=36 x 3+12 x © Kjell Erik Skaug, Hi. A Eksempel 4 y=sin(x 2+x) y=sinu og u= x 2+x y`=dy/du*du/dx= cosu (2 x+1) y`=(2 x+1)cos(x 2+x) eller rett fram y`=cos(x 2+x)(2 x+1) a b c a derivert av ytre funksjon b indre funksjon uendret c derivert av indre funksjon 13

HØGSKOLEN I AGDER Agder University College Eksempel kjerneregelen Eksempel 5 g(t)=tan(5 -sin 2 t) setter g(u)=tan u og u(v)= 5 -sinv og v(t)=2 t g`(u)=1/cos 2 u og u`(v)= -cosv og v`(t)=2 © Kjell Erik Skaug, Hi. A 14

HØGSKOLEN I AGDER Agder University College Implisitt derivasjon brukes når funksjonsuttrykket inneholder uttrykk med både x og y. Ved derivasjon behandles y som en deriverbar funksjon av x og så deriveres begge sider av likningen. Eksempel 2 y 2=x 2+sin(xy) deriverer 2 y*dy/dx = 2 x+cos(xy)(y+x*dy/dx) 2 y*dy/dx=2 x+ycos(xy)+x*dy/dx *cos(xy) (2 y-xcos(xy)*dy/dx = 2 x + ycos(xy) dy/dx = (2 x + y*cos(xy) / (2 y – x*cos(xy) © Kjell Erik Skaug, Hi. A 15

HØGSKOLEN I AGDER Agder University College Eksempel 3 x 3+ y 3 – 9 xy = 0 Tangent i punktet (2, 4) er på kurven: 23+43 -9*2*4 = 8 + 64 – 72 = 0 Deriverer: 3 x 2 + 3 y 2* y`- 9 y – 9 xy`= 0 (3 y 2 – 9 x)y`= 9 y – 3 x 2 Tangent i (2, 4) y – 4 = 4/5 (x – 2) y = 4/5 x – 8/5 +4 = 4/5 x + 12/5 Normal: m 1 * m 2 = -1 m 2 = - 1/m 1 = - 5/4 y – 4 = -5/4 ( x – 2) y = -5/4 x + 26/4 © Kjell Erik Skaug, Hi. A 16