Grade 4 Linear Equations Solve linear equations with




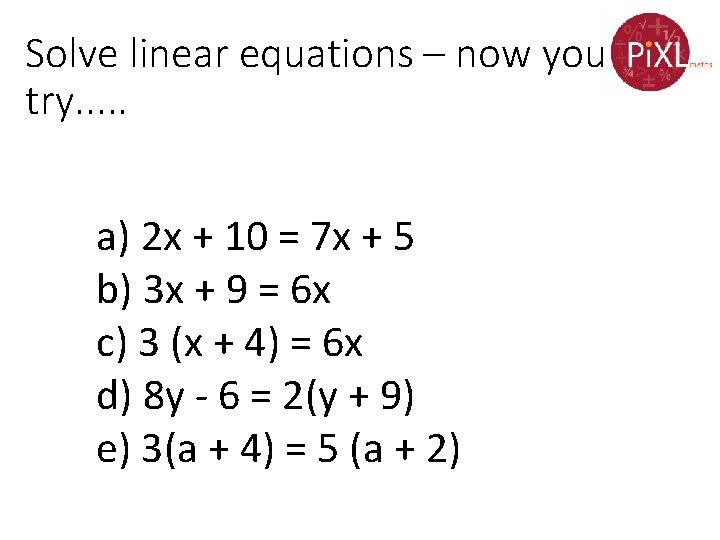







- Slides: 17

Grade 4 Linear Equations Solve linear equations with one unknown on both sides and those involving brackets If you have any questions regarding these resources or come across any errors, please contact helpful-report@pixl. org. uk

Key Vocabulary Solve Linear Equations Unknown

How to solve linear equations with one unknown on both sides 1) 2 x + 12 = 7 x + 2 - 2 x 12 = 5 x + 2 -2 10 = 5 x ÷ 5 2=x -2

How to solve linear equations with one unknown on both sides 2) 7 x + 8 = 9 x - 7 x 8 = 2 x ÷ 2 4=x

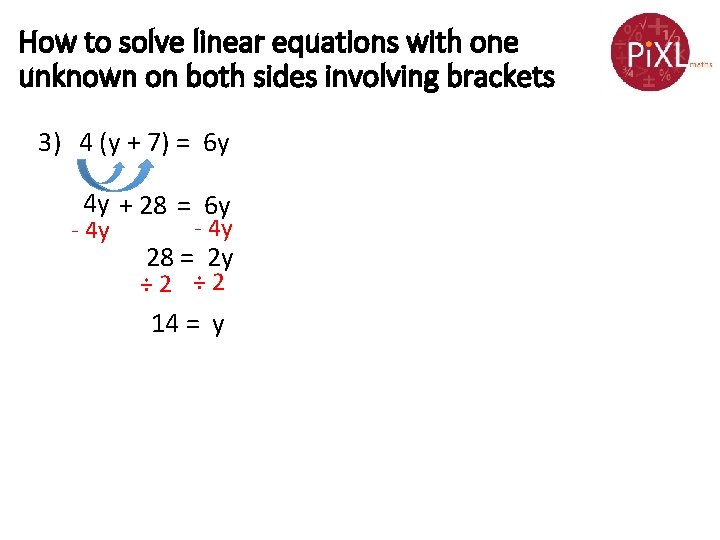
How to solve linear equations with one unknown on both sides involving brackets 3) 4 (y + 7) = 6 y 4 y + 28 = 6 y - 4 y 28 = 2 y ÷ 2 14 = y

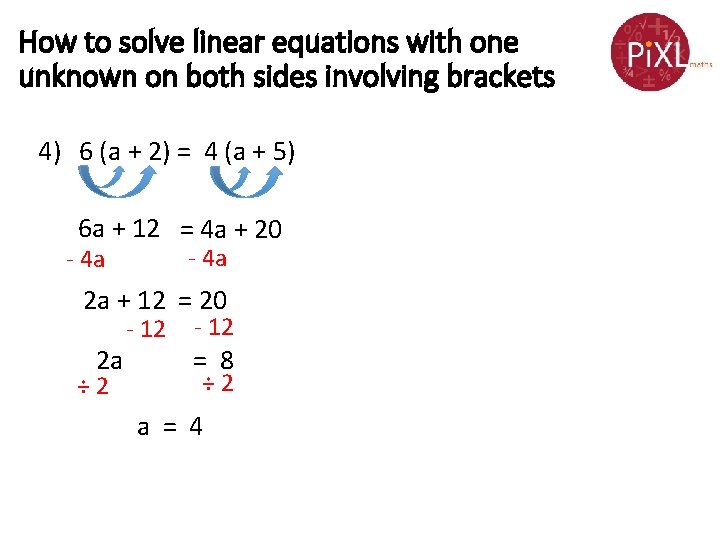
How to solve linear equations with one unknown on both sides involving brackets 4) 6 (a + 2) = 4 (a + 5) 6 a + 12 = 4 a + 20 - 4 a 2 a + 12 = 20 2 a ÷ 2 - 12 = 8 ÷ 2 a = 4
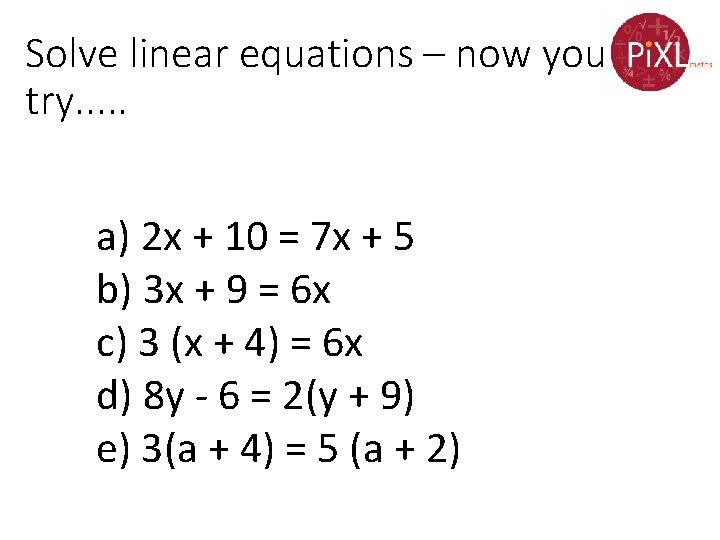
Solve linear equations – now you try. . . a) 2 x + 10 = 7 x + 5 b) 3 x + 9 = 6 x c) 3 (x + 4) = 6 x d) 8 y - 6 = 2(y + 9) e) 3(a + 4) = 5 (a + 2)

Solve linear equations – now you try. . . a) 2 x + 10 = 7 x + 5 b) 3 x + 9 = 6 x c) 3 (x + 4) = 6 x d) 8 y - 6 = 2(y + 9) e) 3(a + 4) = 5 (a + 2) x=1 x=3 x=4 y=4 a=1

More Practice Solving Linear Equations a) 3 x - 8 = x + 2 b) 2 x + 12 = 6 x c) 5 + 3 x = 9 x – 4 d) 2 (a + 5) = 6 ( a – 5) e) 5 (y – 6) = 2 ( 6 + y) f) 4 b = 6 b - 12

More Practice Solving Linear Equations a) 3 x - 8 = x + 2 b) 2 x + 12 = 6 x c) 5 + 3 x = 9 x – 4 d) 2 (a + 5) = 6 ( a – 5) e) 5 (y – 6) = 2 ( 6 + y) f) 4 b = 6 b - 12 x=5 x=3 x = 1. 5 a = 10 y = 14 b=6

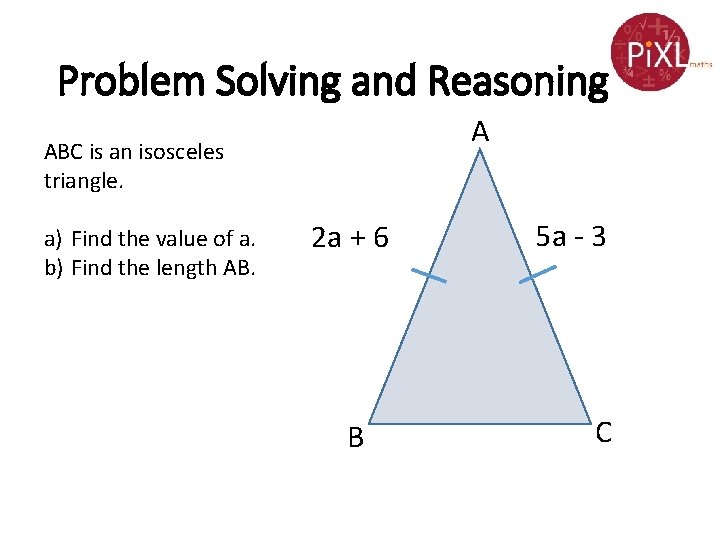
Problem Solving and Reasoning A ABC is an isosceles triangle. a) Find the value of a. b) Find the length AB. 2 a + 6 B 5 a - 3 C

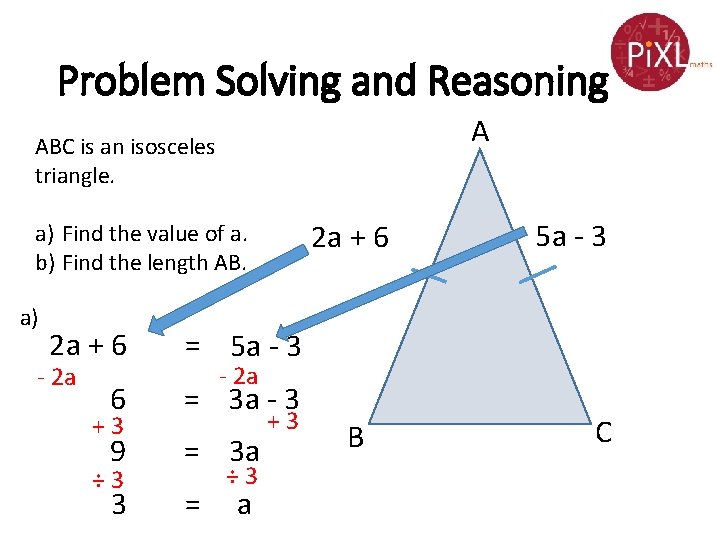
Problem Solving and Reasoning A ABC is an isosceles triangle. 2 a + 6 a) Find the value of a. b) Find the length AB. a) 2 a + 6 = 5 a - 3 6 = 3 a - 3 9 = 3 a 3 = - 2 a +3 ÷ 3 5 a - 3 - 2 a ÷ 3 a +3 B C

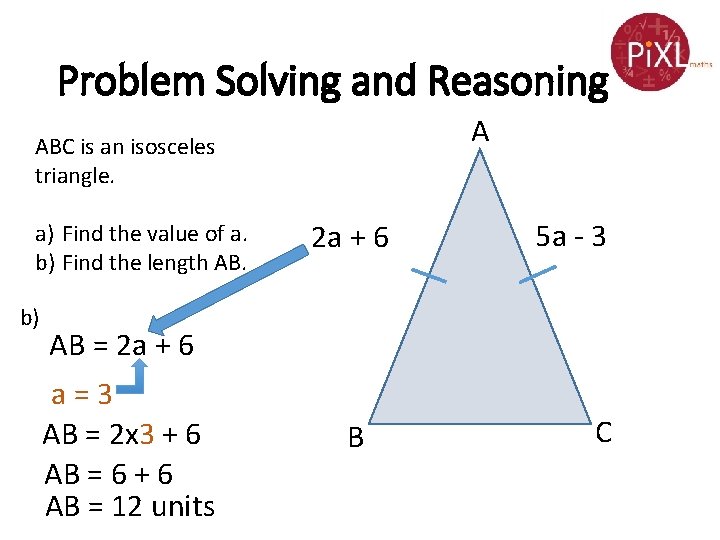
Problem Solving and Reasoning A ABC is an isosceles triangle. a) Find the value of a. b) Find the length AB. b) 2 a + 6 5 a - 3 AB = 2 a + 6 a=3 AB = 2 x 3 + 6 AB = 6 + 6 AB = 12 units B C

Problem Solving and Reasoning Carl thinks of a number. He multiplies this by 3 then adds 23. Liz thinks of a number and she adds 3, then she multiplies this by 5. The number they chose and sums at the end are equal. What is the number they have picked?

Problem Solving and Reasoning Carl thinks of a number. He multiplies this by 3 then adds 23. Liz thinks of a number and she adds 3, then she multiplies this by 5. The number they chose and sums at the end are equal. What is the number they have picked? They think of the same number to start with, lets say x. Carl’s expression => 3 x + 23 Liz’s expression => 5(x + 3) 3 x + 23 = 5 x + 15 23 = 2 x + 15 8 = 2 x 4=x They thought of number 4.

Reason and explain • Explain why 3(2 x + 4) = 6(x + 1) cannot be solved. • Is there a way of checking whether our answers are correct? • Spot the mistake: 3 (b - 2) = 4 (b + 1) 3 b + 6 = 4 b + 4 - 3 b 6=b+4 -6 b= 2 -6

Reason and explain • Explain why 3(2 x + 4) = 6(x + 1) cannot be solved. • Is there a way of checking whether our answers are correct? • Spot the mistake: 3 (b - 2) = 4 (b + 1) 3 b + 6 = 4 b + 4 - 3 b 6=b+4 -6 b= 2 -6
 Solving a system of equations calculator
Solving a system of equations calculator Characteristic equation
Characteristic equation What is ordinary differential equation
What is ordinary differential equation Simultaneous nonlinear equations
Simultaneous nonlinear equations What is linear equation
What is linear equation X2+(y-3√x2)2=1
X2+(y-3√x2)2=1 Contoh simultan
Contoh simultan Difference between linear and nonlinear equation
Difference between linear and nonlinear equation Solve for x grade 9
Solve for x grade 9 Write a one-step equation: word problems
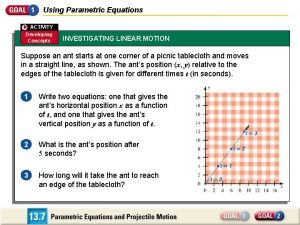
Write a one-step equation: word problems Parametric equations activity
Parametric equations activity Solve a system of equations using elimination
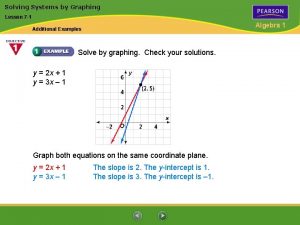
Solve a system of equations using elimination Lesson 7 solve systems of equations by graphing
Lesson 7 solve systems of equations by graphing Steps to solve system of equations
Steps to solve system of equations Solving square root and other radical equations quick check
Solving square root and other radical equations quick check Solving rational equations and inequalities
Solving rational equations and inequalities Discriminant formula
Discriminant formula Square root method formula
Square root method formula