Solve equations in 2 variable Solve equations in
Solve equations in 2 variable Solve equations in 3 variables Matrices Operations Word problems 1 1 2 2 3 3

Solve the system of equations: Solving the first equation for x, we find x = 3 y – 1. Substituting this value of x into the second equation yields Substituting this value of y into the first equation gives. Therefore, the unique solution of the system is (2, 1).

Solve the system of equations The solution to the system is thus x = 3, y = 4, and z = 1.

Given the matrix find 5 A.

The market share of motorcycles in the United States in 2001 follows: Honda 27. 9%, Harley-Davidson 21. 9%, Yamaha 19. 2%, Suzuki 11%, Kawasaki 9. 1%, and others 10. 9%. The corresponding figures for 2002 are 27. 6%, 23. 3%, 18. 2%, 10. 5%, 8. 8%, and 11. 6%, respectively. Express this information using a 2 x 6 matrix.
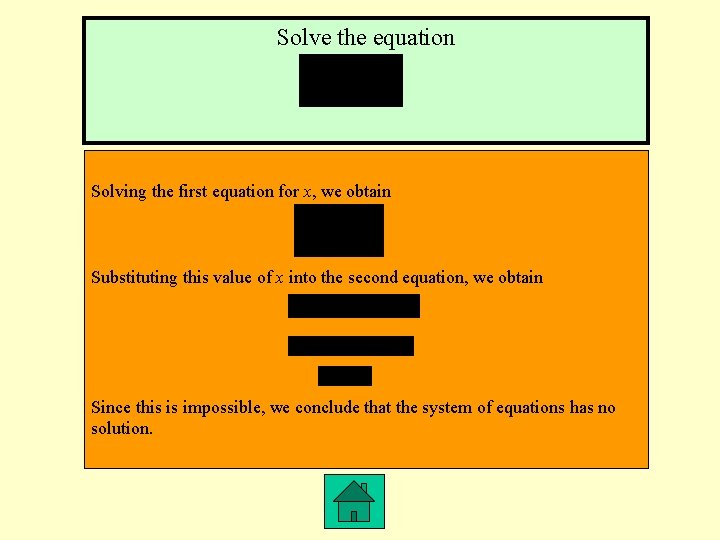
Solve the equation Solving the first equation for x, we obtain Substituting this value of x into the second equation, we obtain Since this is impossible, we conclude that the system of equations has no solution.

Solve the system If we let z = t then the solution is given by (1 + 2 t, t, t)

Given matrices A and B, find A + 2 B

Michael Perez has a total of $2000 on deposit with two savings institutions. One pays interest at the rate of 6%/year, whereas the other pays interest at the rate of 8%/year. If Michael earned a total of $144 interest during a single year, how much does he have on deposit in each institution? We wish to solve the system of equations x + y = 2000 (x = the amount invested at 6 percent) 0. 06 x + 0. 08 y = 144 (y = the amount invested at 8 percent) Using the Gauss-Jordan method, we find the solution to this system of equations is x = 800 and y = 1200.

Solve the equation Solving the first equation for x, we have 5 x = 6 y + 8 Substituting this value of x into the second equation, gives 12 y + 16 – 12 y = 16 or 0 = 0. Thus, by assigning the value t to x, where t is any real number, we find that. So the ordered pair, is a solution to the system.
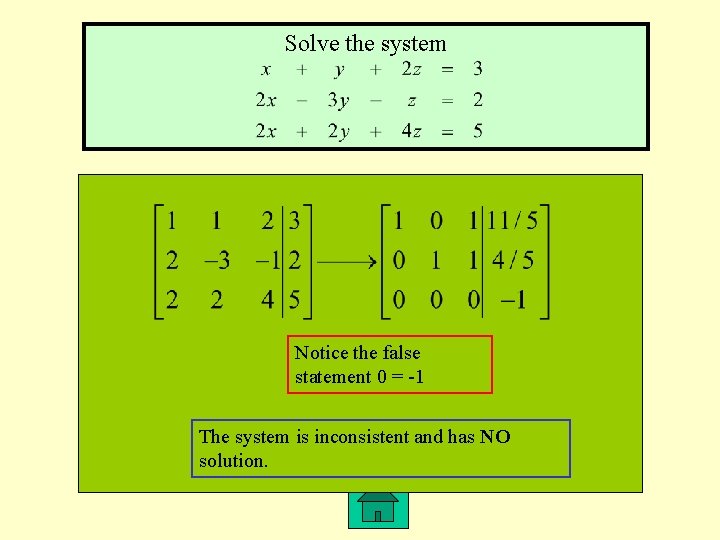
Solve the system Notice the false statement 0 = -1 The system is inconsistent and has NO solution.

Solve for u, x, y and z in the matrix by the definition of equality of matrices,

A private investment club has $200, 000 earmarked for investment stocks. To arrive at an acceptable overall lever of risk, the stocks that management is considering have been classified into three categories: high risk, medium risk, and low risk. Management estimates that high-risk stocks will have a rate of return of 15%/year; medium-risk stocks, 10%/year; and low-risk stocks, 6%/year. The members have decided that the investment in low-risk stocks should be equal to the sum of the investments in the stocks of the other two categories. Determine how much the club should invest in each type of stock if the investment goal is to have a return of $20, 000/year on the total investment. Let x, y, and z denote the amount to be invested in high-risk, mediumrisk, and low-risk stocks, respectively. We see that x = 80, 000, y = 20, 000, and z = 100, 000. Therefore, they should invest $80, 000 in high-risk, $20, 000 in medium-risk, and $100, 000 in low-risk stocks.
- Slides: 13

























