Solving linear equations LO To solve linear equations

Solving linear equations LO: To solve linear equations www. mathssupport. org

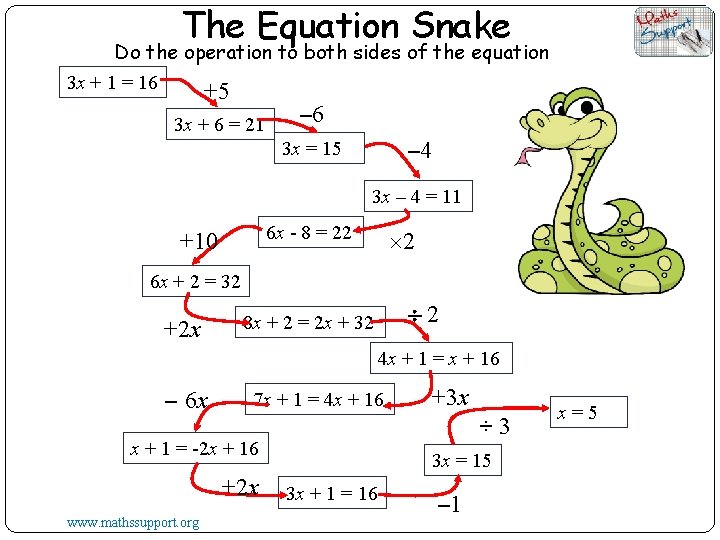
The Equation Snake Do the operation to both sides of the equation 3 x + 1 = 16 +5 3 x + 6 = 21 – 6 – 4 3 x = 15 3 x – 4 = 11 6 x - 8 = 22 +10 2 6 x + 2 = 32 +2 x 2 8 x + 2 = 2 x + 32 4 x + 1 = x + 16 – 6 x 7 x + 1 = 4 x + 16 ÷ 3 x + 1 = -2 x + 16 +2 x www. mathssupport. org +3 x 3 x = 15 3 x + 1 = 16 – 1 x=5

Solving linear equations An equation means that two things are equal. A linear equation is an equation which contains a variable which is not raised to any power other than 1. The solutions of an equation are the values of the variable which make the equation true The Left-hand side of an equation (LHS) is on the left of the = sign The Right-hand side of an equation (RHS) is on the right of the = sign www. mathssupport. org

Equations – Keep it balanced An equation means that two things are equal. We can compare equations to a set of scales. If the scales balance, then the value of each side must be equal. www. mathssupport. org

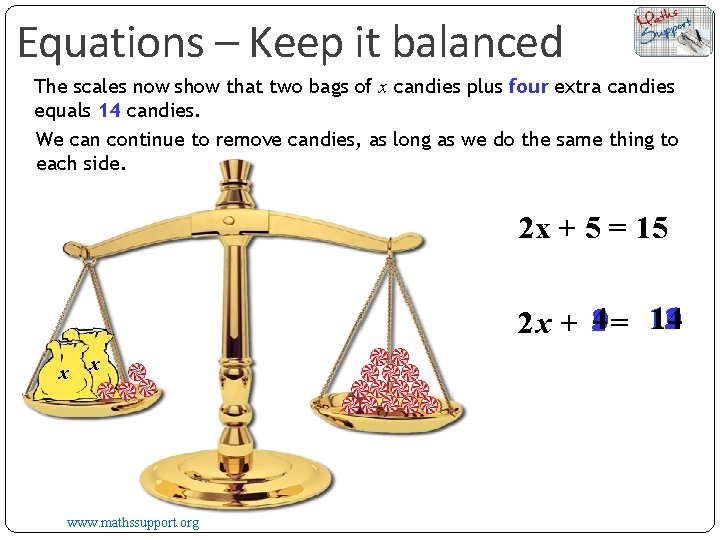
Equations – Keep it balanced Two bags of x candies plus five extra candies equals 15 candies. If we remove a candy from one side, we must remove a candy from the other side so that the scales still balance. 2 x + 5 = 15 Take off 1 2 x +4 = 14 x x www. mathssupport. org

Equations – Keep it balanced The scales now show that two bags of x candies plus four extra candies equals 14 candies. We can continue to remove candies, as long as we do the same thing to each side. 2 x + 5 = 15 11 12 10 14 2 x + 14230 = 13 x x www. mathssupport. org

Equations – Keep it balanced The scales now show that two bags of x candies equals 10 candies. We can’t remove any more candies, but we can halve the values on each side. 2 x + 5 = 15 ÷ 2 x x www. mathssupport. org ÷ 2 2 x = 10 x=5

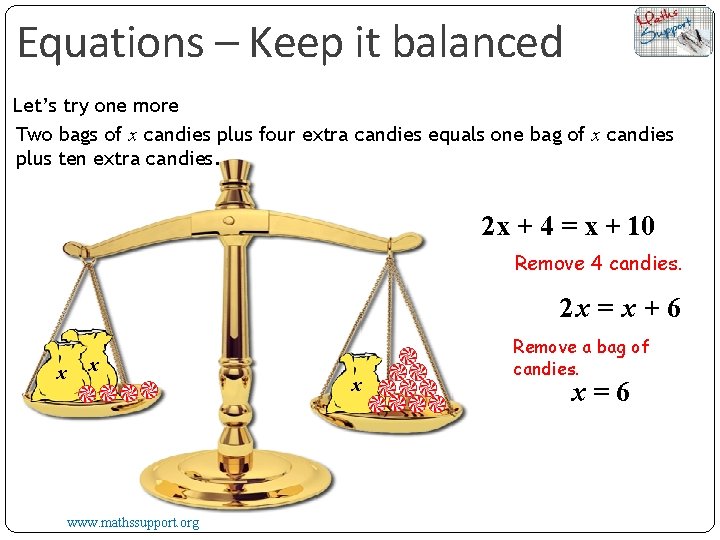
Equations – Keep it balanced Let’s try one more Two bags of x candies plus four extra candies equals one bag of x candies plus ten extra candies. 2 x + 4 = x + 10 Remove 4 candies. 2 x = x + 6 x x www. mathssupport. org x Remove a bag of candies. x=6

When solving equations, try to imagine the scales. To make sure the equation balances … Whatever we do to one side of the equation we must do to the other, in order to isolate the unknown. We consider how the expression has been built up and then isolate the unknown by using inverse operations in reverse order, For example For the equation 2 xx + 6 = 10 The LHS is built up by starting with x 2 2 x 2 x + 6 So, to isolate x, we first subtract 6 from both sides Then divide both sides by 2 2 x + 6 = 10 +6 2 – 6 2 x + 6 – 6 = 10 – 6 2 x = 4 2 www. mathssupport. org 2 x =2

Solving linear equations Whatever we do to one side of the equation we must do to the other. Example 1: 3 x + 7 = 22 – 7 3 x = 15 3 Subtracting 7 from both sides 3 x=5 www. mathssupport. org Dividing both sides by 3

Solving linear equations Whatever we do to one side of the equation we must do to the other. Example 2: Subtracting 11 from both sides – 11 – 5 www. mathssupport. org Dividing both sides by -5

Solving linear equations Whatever we do to one side of the equation we must do to the other. Example 3: Subtracting 2 from both sides – 2 3 www. mathssupport. org 3 Multiplying both sides by 3

Solving linear equations Whatever we do to one side of the equation we must do to the other. Example 4: 5 5 4 x + 3 = – 10 – 3 4 x = – 13 4 www. mathssupport. org 4 Multiplying both sides by 5 Subtracting 3 from both sides Dividing both sides by 4

Equations with unknown on both sides Equations where the unknown appears more than once need to be solved systematically. If necessary, expand any brackets and collect like terms. If necessary, remove the unknown from one side of the equation. Aim to do this so the unknown is left with a positive coefficient. Use inverse operations to isolate the unknown and maintain balance. Check that your solution satisfies the equation. www. mathssupport. org

Equations with unknown on both sides The equation can then be solved by performing the same operations on both sides until the solution is found. 5 x – 4 = 2 x + 14 +4 add 4 to both sides: +4 5 x = 2 x + 18 subtract 2 x from both sides: – 2 x 3 x = 18 divide both sides by 3: ÷ 3 x=6 Check by substituting x = 6 into the expressions in the original equation. Both sides are equal to 2, so the solution is correct. www. mathssupport. org

Equations with brackets Solve the equation: 5 – 3(– 1 + x) = x Expand the brackets: simplifying 5 + 3 – 3 x = x 8 – 3 x = x Subtracting 8 from both sides: – 3 x = x – 8 subtracting x from both sides: – 4 x = – 8 dividing both sides by -4: www. mathssupport. org x=2

Equations with brackets Solve the equation: ( x – 3)2 = (4 + x) (2 + x) Expand each side: Subtracting x 2 from both sides x 2 – 6 x +9 = 8 + 4 x + 2 x + x 2 – 6 x +9 = 8 + 4 x + 2 x – 6 x +9 = 8 + 6 x adding 6 x to both sides: 9 = 8 + 12 x subtracting 8 from both sides: 1 = 12 x dividing both sides by 12: 1= x 12 www. mathssupport. org

Thank you for using resources from For more resources visit our website https: //www. mathssupport. org If you have a special request, drop us an email info@mathssupport. org Get 20% off in your next purchase from our website, just use this code when checkout: MSUPPORT_20 www. mathssupport. org