Goal Plan Explore space complexity Low space classes

Goal: Plan: • Explore space complexity • • Low space classes: L, NL Savitch’s Theorem Immerman’s Theorem TQBF 1

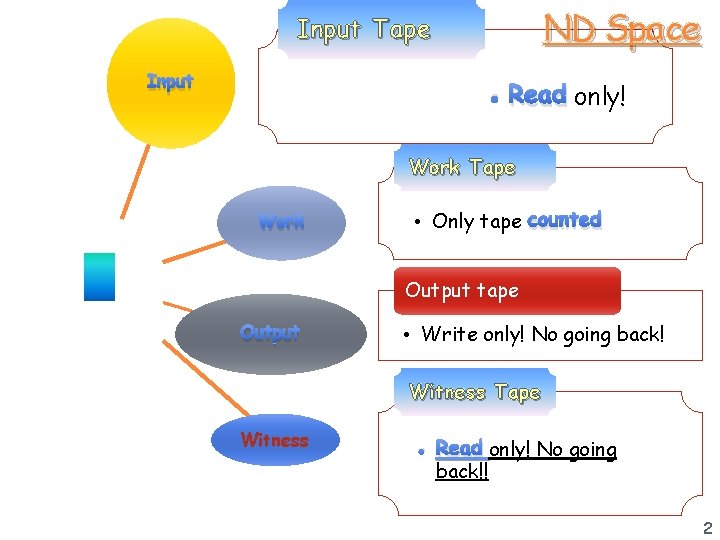
ND Space Input Tape Input • Read only! Work Tape Work • Only tape counted Output tape Output • Write only! No going back! Witness Tape Witness • Read only! No going back!! 2

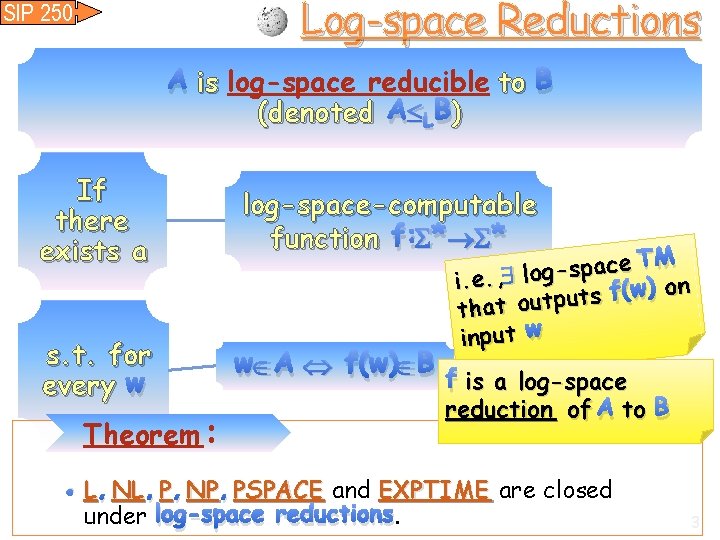
Log-space Reductions SIP 250 A is log-space reducible to B (denoted A L B)) If there exists a log-space-computable function f: * * s. t. for every w w A f(w) B f is a log-space Theorem : e TM c a p s g o l i. e. , on ) w ( f s t u p that out input w reduction of A to B • L , NL , P , NP , PSPACE and EXPTIME are closed under log-space reductions. 3

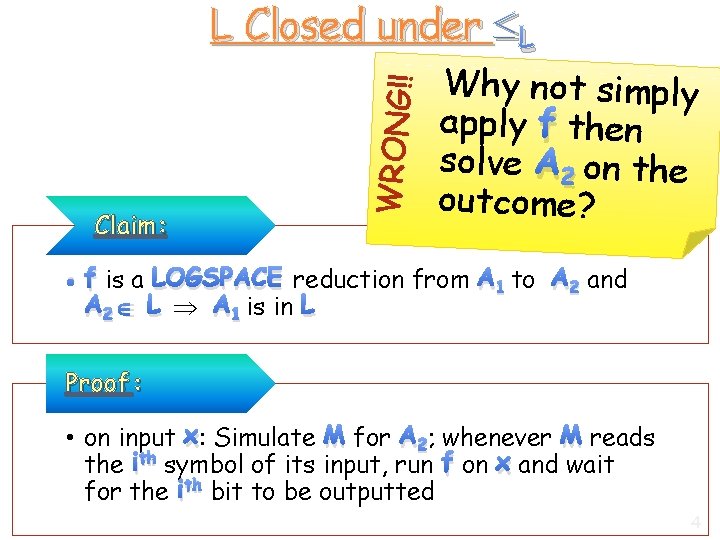
Claim: WRONG!! L Closed under L Why not simply apply f then solve A 2 on the outcome? • f is a LOGSPACE reduction from A 1 to A 2 and A 2 L A 1 is in L Proof : • on input x: Simulate M for A 2; whenever M reads the ith symbol of its input, run f on x and wait for the ith bit to be outputted 4

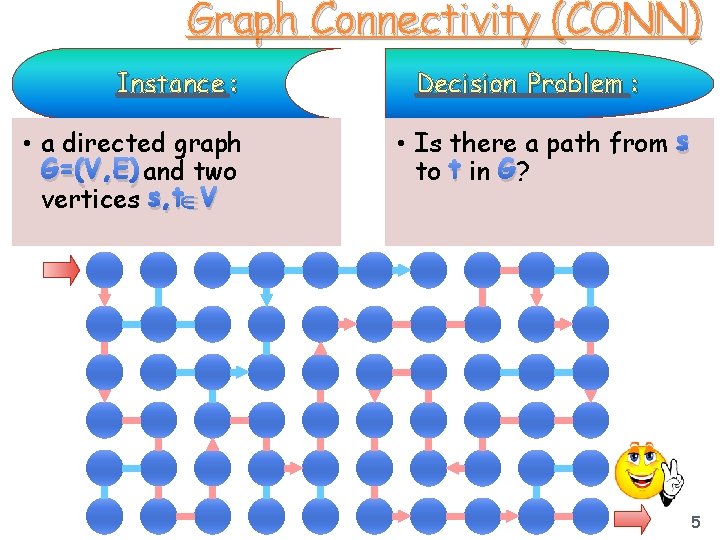
Graph Connectivity (CONN) Instance : • a directed graph G=(V, E) and two vertices s, t V Decision Problem : • Is there a path from s to t in G? 5

1 • Let u=s current position requires log|V| space 2 • Begin For i = 1, . . , |V| CONN NL counting to |V| ce a p s | V | g lo s e r i u q re 3 • Let u= a ( non-deterministic ) neighbor of u 4 • accept if u=t 5 • End For 6 • reject (did not reach t) 6

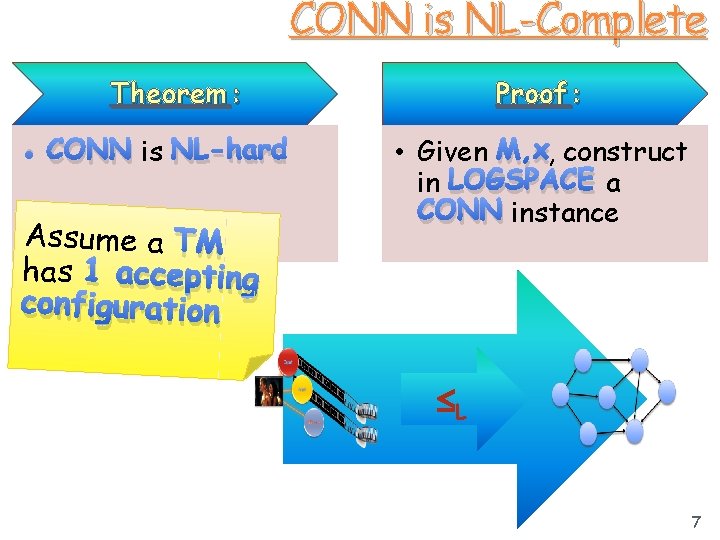
CONN is NL-Complete Theorem : • CONN is NL-hard Assume a TM has 1 accepting configuration Proof : • Given M, x, construct in LOGSPACE a CONN instance L 7

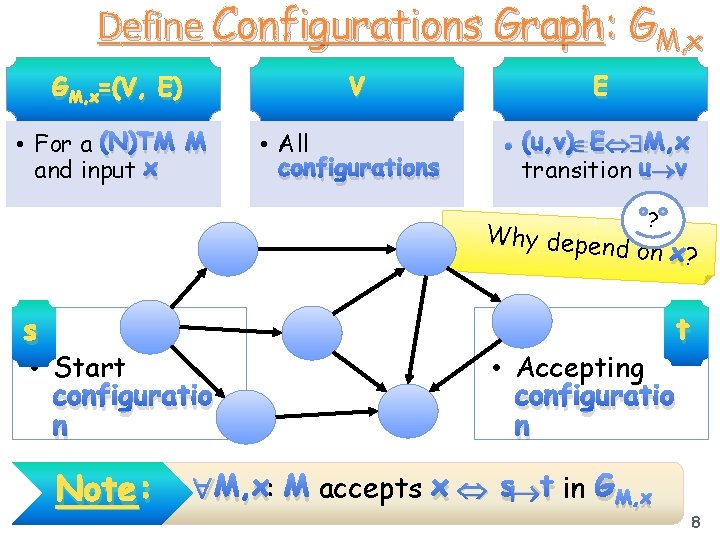
Define Configurations Graph: GM, x=(V, E) • For a (N)TM M and input x V • All configurations E • (u, v) E M, x transition u v Why depen ? d on x? s • Start configuratio n • Accepting configuratio n Note: • M, x: M accepts x s t in GM, x t 8

CONN is NL-Complete Proof (end) : • GM, x can be constructed in Log-Space Corollary : • NL P Proof: • CONN P EX PS P PA CE N P P N L L 9

Where do I belong? sat matching stcon ustcon anbn Find L N n i m e l b o A pr o t n w o n k t o N be in L EX PS P PA CE N P P N L L 10

Now • that we have a language – CONN– representing NL We can • better analyze the complexity of spacebounded computations 11

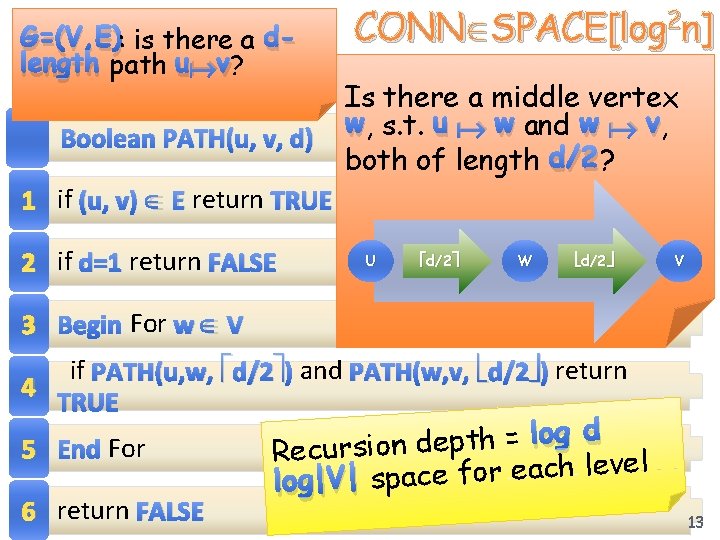
Theorem: Savitch’s Theorem • NL DSPACE[log 2 n] • S(n) ≥ log(n): NSPACE[S(n)] SPACE[S(n)2] • NPSPACE=PSPACE Proof (first item) : • Suffices to show CONN DSPACE[log 2 n] 12

G=(V, E): is there a dlength path u v? • Boolean PATH(u, v, d) CONN SPACE[log 2 n] Is there a middle vertex w, s. t. u w and w v, both of length d/2? 1 • if (u, v) E return TRUE 2 • if d=1 return FALSE U d/2 W d/2 V 3 • Begin For w V • if PATH(u, w, d/2 ) and PATH(w, v, d/2 ) return 4 TRUE 5 • End For 6 • return FALSE d g lo = h t p e d n o i s r u c Re el v le h c a e r o f e c a p log|V| s 13

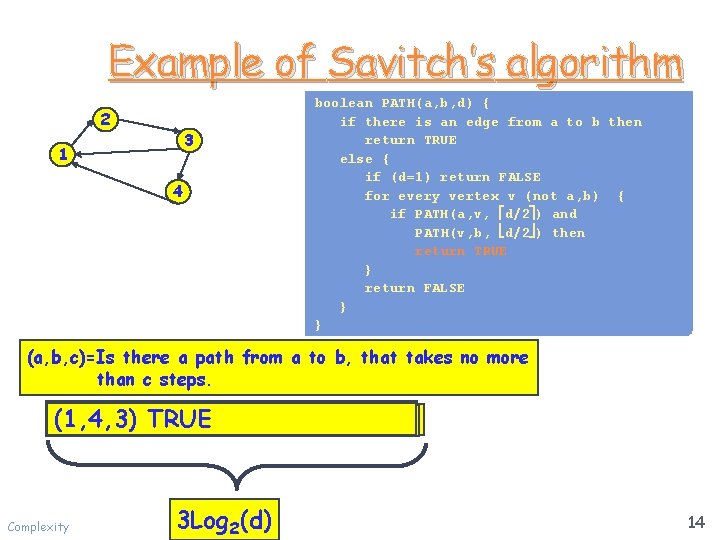
Example of Savitch’s algorithm 2 3 1 4 boolean PATH(a, b, d) { if if there is is an an edge from a to b then if there is an edge from aa to to bb then if there is an edge from a to b then return TRUE return TRUE else { if (d=1) return FALSE if (d=1) return FALSE for every vertex v (not a, b) { for every vertex vv (not a, b) {{ for every vertex v (not a, b) { if if PATH(a, v, d/2 ) and PATH(v, b, d/2 ) then PATH(v, b, d/2 ) then return TRUE } }} } return FALSE return FALSE } }}} (a, b, c)=Is there a path from a to b, that takes no more than c steps. (1, 4, 3)(2, 4, 1) (1, 4, 3)(1, 3, 2)(1, 2, 1)TRUE (1, 4, 3)(1, 3, 2)(1, 2, 1) (1, 4, 3)(3, 4, 1)TRUE (1, 4, 3)(1, 3, 2) (1, 4, 3)(1, 2, 2)TRUE (1, 4, 3)(1, 3, 2)(2, 3, 1) (1, 4, 3)(1, 2, 2) (1, 4, 3)(2, 4, 1)FALSE TRUE (1, 4, 3)(1, 3, 2)(2, 3, 1)TRUE (1, 4, 3)(3, 4, 1) (1, 4, 3)(1, 3, 2)TRUE Complexity 3 Log 2(d) 14

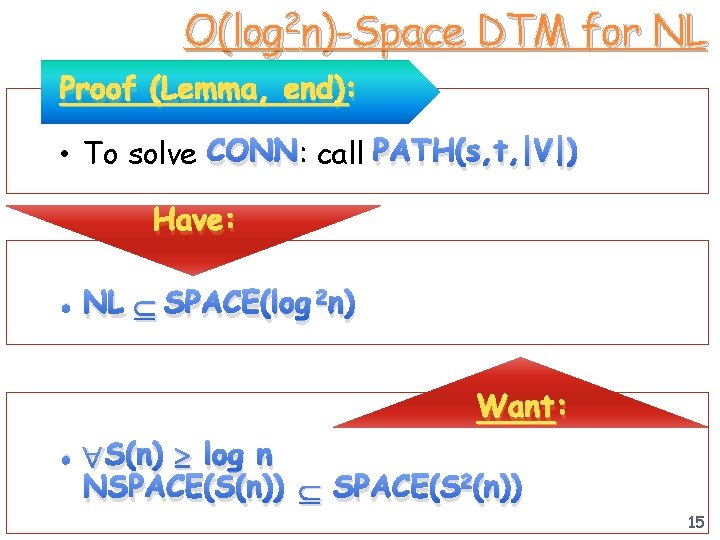
O(log 2 n)-Space DTM for NL Proof (Lemma, end): • To solve CONN: call PATH(s, t, |V|) Have: • NL SPACE(log 2 n) Want: • S(n) log n NSPACE(S(n)) SPACE(S 2 (n)) 15

Scale up Claim: • For any two space constructible functions s 1(n), s 2 (n) logn, e(n) n: If • NSPACE[s 1(n)] SPACE[s 2(n)] Then • NSPACE[s 1(e(n))] SPACE[s 2(e(n))] 16

Proof: Padding argument • For L NSPACE[s 1(e(n))] , let Le = {X # e(|x|)-|x| | X L}; Claim 1: Premise • Le NSPACE[s 1(n)] DSPACE[s 2(n)] Hence • M’ of s 2(n)-DSPACE for Le M’ counts |X| and #’s to ensure proper form, then treat # as _ M simulates M’ and Claim 2: “cheats” it to “see” e(|X|)-|X| extra #’s • M of s 2(e(n))-DSPACE for L 17

Padding DSPACE[s 2(e(|X|))] TM M for L: simulate M’ “as if” suffixed w/ e(|X|)-|X| # ’s appended D N S SPPA ACCE E[s [s 21(| (|XX# #. . . ##||)])]TTM M M’ for Le: check input=X input= #e(|X|)-|X| ; call M” X X#. . # X Yes M” for L )] ) | X | ( e ( s NSPACE[ 1 TM No 18

So far Next • Simulation of Non-deterministic space-bounded computation does not incur very large overhead • What about complementation ? NL vs. co. NL 19

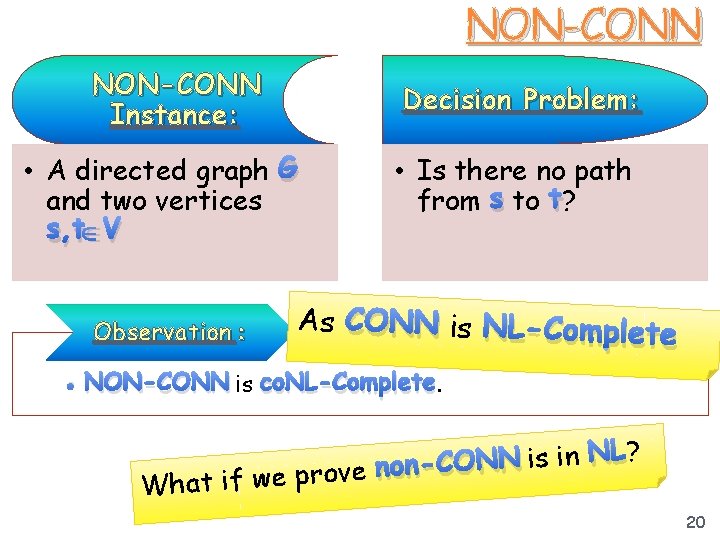
NON-CONN Instance: Decision Problem: • A directed graph G and two vertices s, t V Observation : • Is there no path from s to t? As CONN is NL-Com plete • NON-CONN is co. NL-Complete. ? L N n i s i N N O n-C o n e v o r p e w f i t Wha 20

When your name’s called How do we know All those present… everyone’s in Raise your hands! attendance Count how many 21

Immerman/Szelepcsényi: co. NL = NL Theorem : • Non-CONN NL Proof: • reachable(G) { v | s v } Def • L N n a e b i r Desc e l b a i f i r e -v t a h t W s witnes no s t there is Def • let G–t (V, E - V{t} ) Witness : • #reachable(G) = #reachable(G–t ) Suffice : • #reachable(G) = r Def • reachablel { v | s v of length l } Induction: • rl=#reachablel Base: r 0=1 W #r l# 22

co. NL = NL Induction step : • Extend an NL-verifiable witness W to “ rl =#reachablel” to a witness to “ rl+1=#reachablel+1”: W #rl # 1 • / reachablel+1 $W W 1$ … Wi for i reachablel+1: • s ii of length l+1 |V| • / reachablel+1 $W W|V| $ Wi for i reachablel+1: 1 … • / reachablel *Z Z 1* Zj for j reachablel only if j ii E: • s jj of length l Ve rif y #{ j rea cha blel } = rl |V| • / reachablel *Z Z|V| * Zj for j reachablel: empty 23

N. D. Algorithm for reachs(v, l) 1. length = l; u = s 2. while (length > 0) { 3. if u = v return ‘YES’ 4. else, for all (u’ V) { 5. if (u, u’) E nondeterministic switch: 5. 1 u = u’; --length; break 5. 2 continue } Takes up logarithmic space } 6. return ‘NO’ Complexity This N. D. algorithm might never stop 24

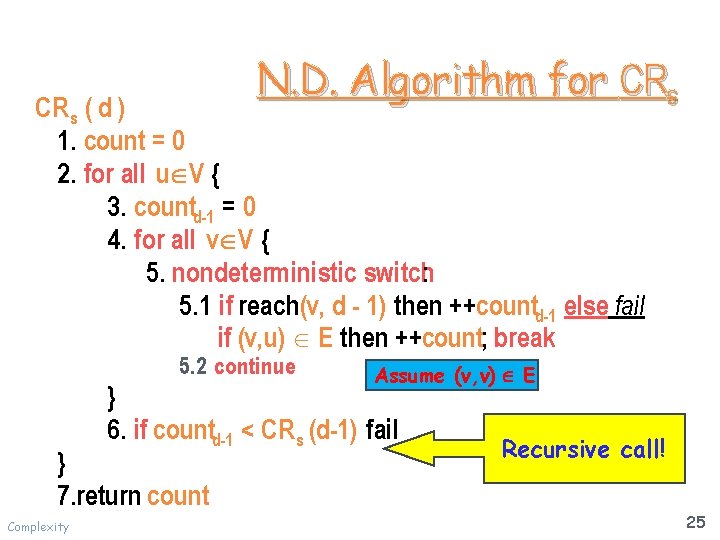
N. D. Algorithm for CRs CR s ( d ) 1. count = 0 2. for all u V { 3. countd-1 = 0 4. for all v V { 5. nondeterministic switch: 5. 1 if reach(v, d - 1) then ++countd-1 else fail if (v, u) E then ++count; break 5. 2 continue Assume (v, v) E } 6. if countd-1 < CR s (d-1) fail } 7. return count Complexity Recursive call! 25

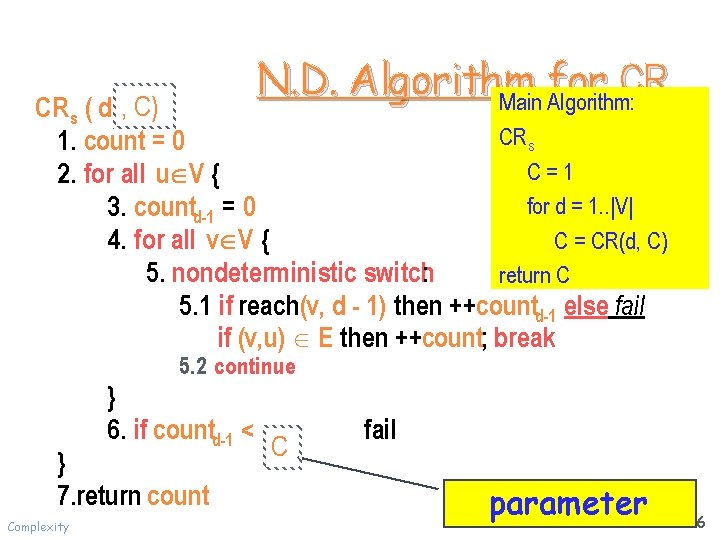
N. D. Algorithm for CR Main Algorithm: s CR s ( d , C) CRs 1. count = 0 C=1 2. for all u V { for d = 1. . |V| 3. countd-1 = 0 C = CR(d, C) 4. for all v V { 5. nondeterministic switch: return C 5. 1 if reach(v, d - 1) then ++countd-1 else fail if (v, u) E then ++count; break 5. 2 continue } 6. if countd-1 < } 7. return count Complexity C fail parameter 26

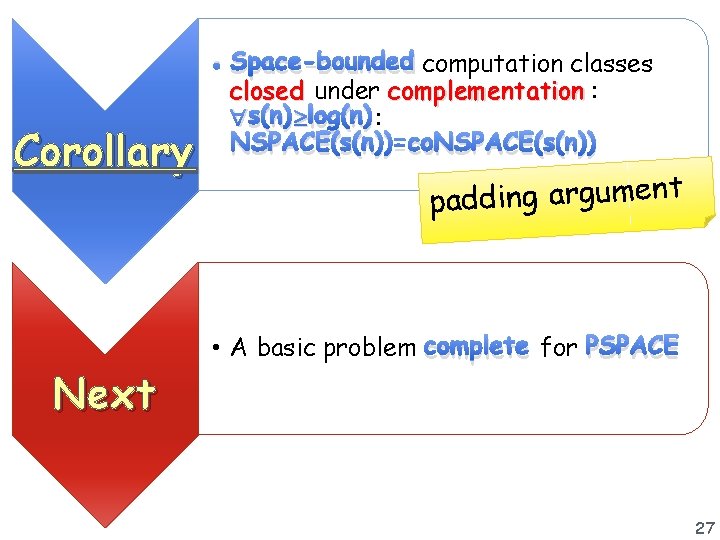
Corollary Next • Space-bounded computation classes closed under complementation : s(n) log(n) : NSPACE(s(n))=co. NSPACE(s(n)) t n e m u g r a g n i d d a p • A basic problem complete for PSPACE 27

Instance : Theorem: • Is true? EG • a fully quantified Boolean formula Decision Problem : TQBF x y)] x y z[(x y z) ( • TQBF PSPACE Proof: • A poly-space algorithm A that evaluates : if is quantifier-free return its value if = x. (x, . . )return A( (0, . . )) A( (1, . . )) 28

Algorithm for TQBF 1 x y[(x y) ( x y)] 1 1 y[(0 y) ( 0 y)] (0 0) ( 0 0) 1 Complexity (0 1) ( 0 1) 0 y[(1 y) ( 1 y)] (1 0) ( 1 0) 0 (1 1) ( 1 1) 1 29

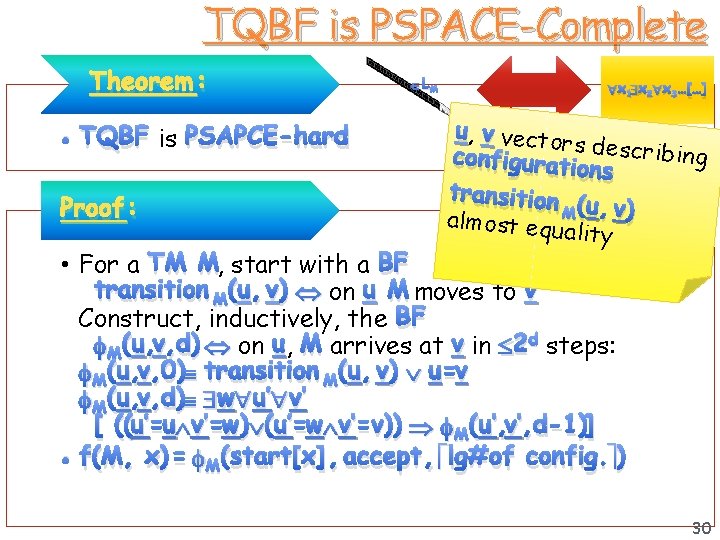
TQBF is PSPACE-Complete Theorem : • TQBF is PSAPCE-hard Proof: LM x 1 x 2 x 3 …[…] u, v vectors d configurati escribing ons transition (u, v) almost equ. M ality • For a TM M, start with a BF transition M (u, v) on u M moves to v Construct, inductively, the BF M (u, v, d) on u, M arrives at v in 2 d steps: M (u, v, 0) transition M (u, v) u=v M (u, v, d) w u’ v’ [ ((u’=u v’=w) (u’=w v’=v)) M (u’, v’, d-1)] • f(M, x) = M(start[x] , accept, lg#of config. ) 30

Synopsis Defined space-complexity, in particular, the complexity classes: L, NL, co. NP, PSPACE. Proved: Completeness : CONN for NL; TQBF for PSPACE Savitch’s theorem ( NL SPACE(log 2 )) The padding argument (scaling up) Immerman’s theorem ( NL=co. NL) 31

Space Complexity Savitch’s Theorem Log Space Reductions Immerman’s Theorem WWindex Savitch, Walter Immerman, Neil TQBF Complexity Classes PSPACE L NL Róbert Szelepcsényi 32