Giovanni Ramrez Javier RodrguezLaguna Germn Sierra Instituto de

Giovanni Ramírez, Javier Rodríguez-Laguna, Germán Sierra Instituto de Física Teórica UAM-CSIC, Madrid Workshop “Entanglement in Strongly Correlated Systems” Centro de Ciencias de Benasque Pedro Pascual, 14 -27 February 2016

If is the ground state of a local Hamiltonian

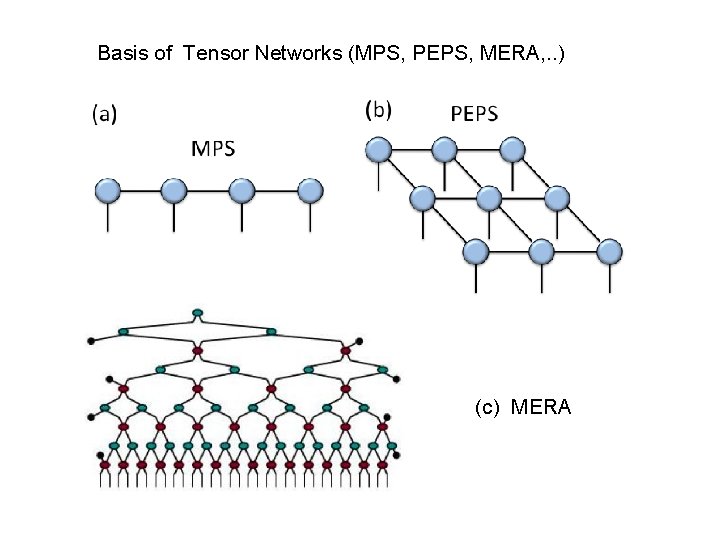
Basis of Tensor Networks (MPS, PEPS, MERA, . . ) (c) MERA

Hastings theorem (2007): In 1 D Conditions: -Finite range interactions -Finite interaction strengths -Existence of a gap in the spectrum In these cases the GS can be well approximated by a MPS (Verstraete, Cirac, Schuch, Perez-Garcia, Vidal, Latorre, Orus, Iblisdir …)

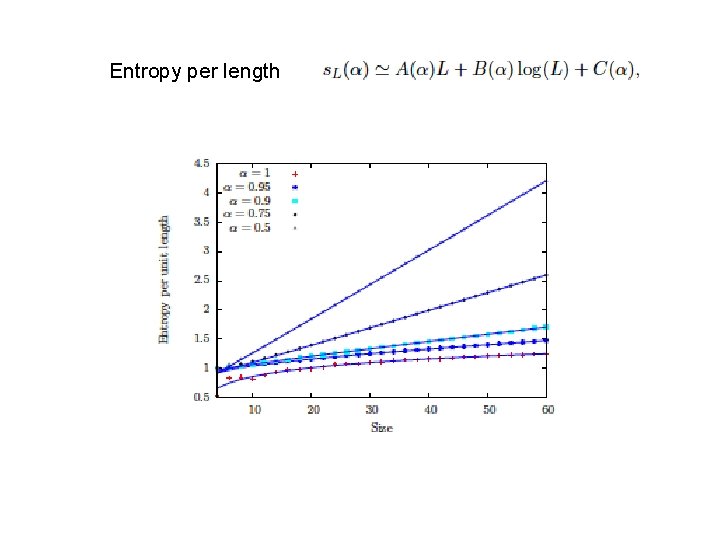
Violations of the area law in 1 D require one of the following - non local interactions - divergent interactions - gapless systems Best well known examples are CFT and quenched disordered systems -> Log violations of entropy Here we shall investigate a stronger violation Entanglement entropy satisfies a volumen law

References: 1) From conformal to volume-law for the entanglement entropy in exponentially deformed critical spin 1/2 chains; J. Stat. Mech. (2014) 2) Entanglement over the rainbow; J. Stat. Mech. (2015) G. Ramírez, J. Rodríguez-Laguna, GS Work in progress with Sebastián Montes

Inhomogenous free fermion model in an open chain with 2 L sites Introduced by Vitigliano, Riera and Latorre (2010) Equivalent to an inhomogenous XX spin chains

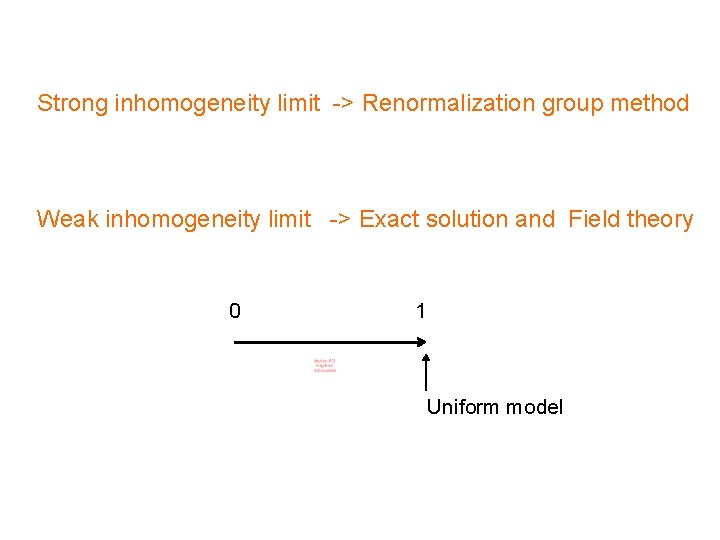
Strong inhomogeneity limit -> Renormalization group method Weak inhomogeneity limit -> Exact solution and Field theory 0 1 Uniform model

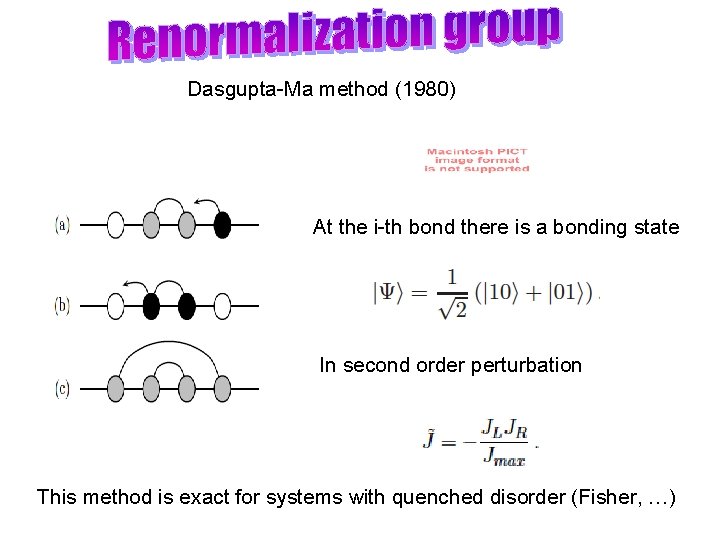
Dasgupta-Ma method (1980) At the i-th bond there is a bonding state In second order perturbation This method is exact for systems with quenched disorder (Fisher, …)

Choosing the J’s at random -> infinite randomness fixed point Average entanglement entropy and Renyi entropies Refael, Moore 04 Laflorencie 05 Fagotti, Calabrese, Moore 11 Ramirez, Laguna, GS 14 CFT Renyi

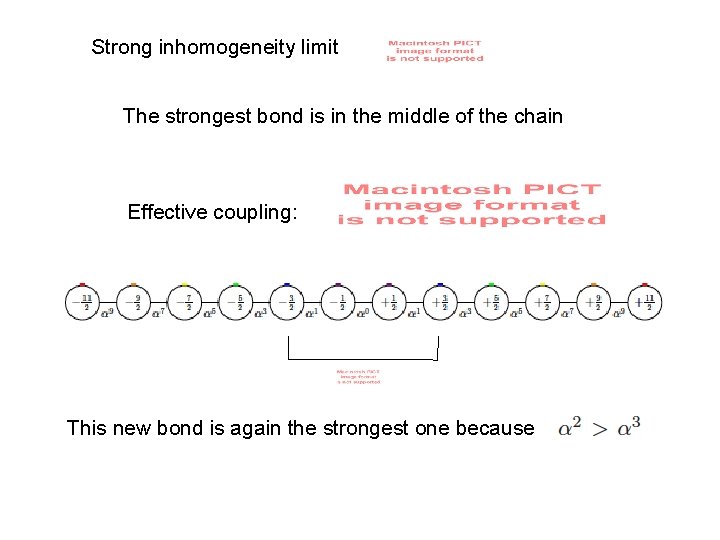
Strong inhomogeneity limit The strongest bond is in the middle of the chain Effective coupling: This new bond is again the strongest one because

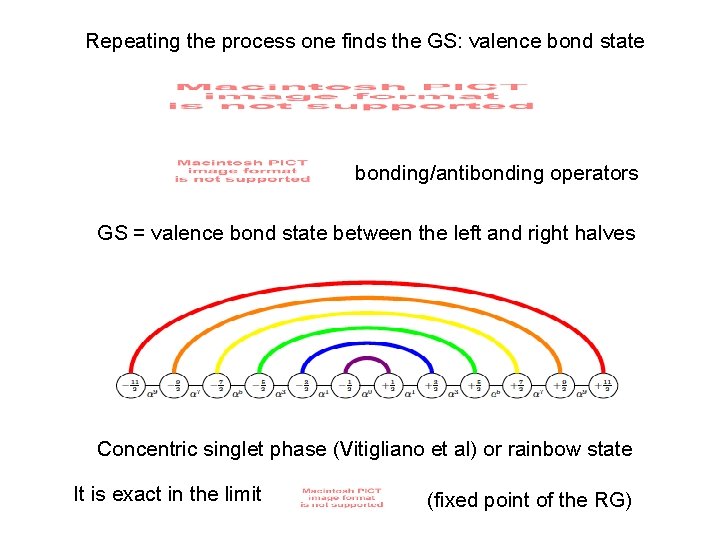
Repeating the process one finds the GS: valence bond state bonding/antibonding operators GS = valence bond state between the left and right halves Concentric singlet phase (Vitigliano et al) or rainbow state It is exact in the limit (fixed point of the RG)

Density matrix of the rainbow state B: a block number of bonds joining B with the rest of the chain has an eigenvalue with multiplicity von Neumann entropy Moreover all Renyi entropies are equal to the von Neumann entropy

Take B to be the half-chain then Maximal entanglement entropy for a system of L qubits The energy gap is proportional to the effective coupling of the last effective bond Hasting’s theorem is satisfied Define Uniform case

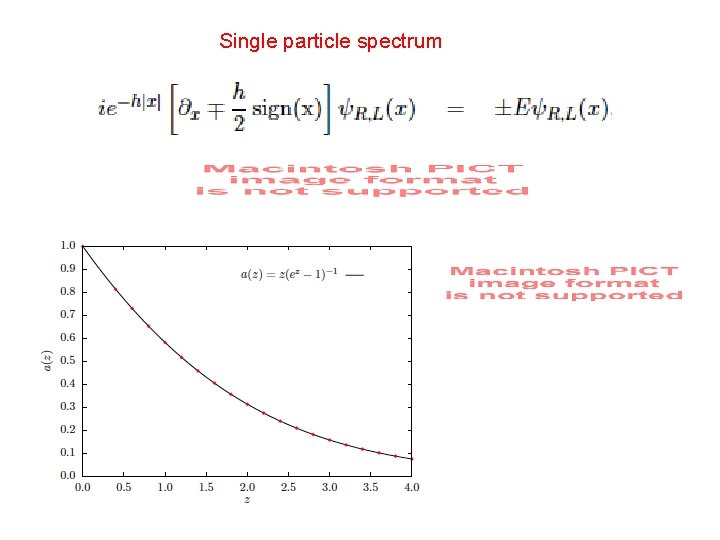
Hopping matrix Particle-hole symmetry Ground state at half-filling

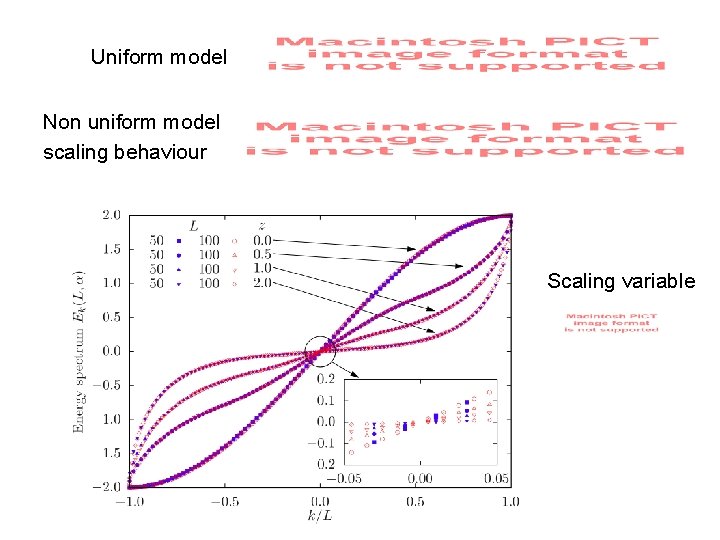
Uniform model Non uniform model scaling behaviour Scaling variable

Correlation method (Peschel, Latorre, Korepin…) Two point correlator in the block B of size Diagonalize finding its eigenvalues Reduced density matrix of the block von Neumann entropy

For small and L large there is a violation of the area law that becomes a volumen law. This agrees with the analysis based on the Dasgupta-Ma RG What about the limit near the critical model?

Uniform model Fast-slow separation of degrees of freedom c=1 CFT with open boundary conditions

Non uniform model Left and right components are decoupled in the bulk but they mixed at the boundary

Single particle spectrum

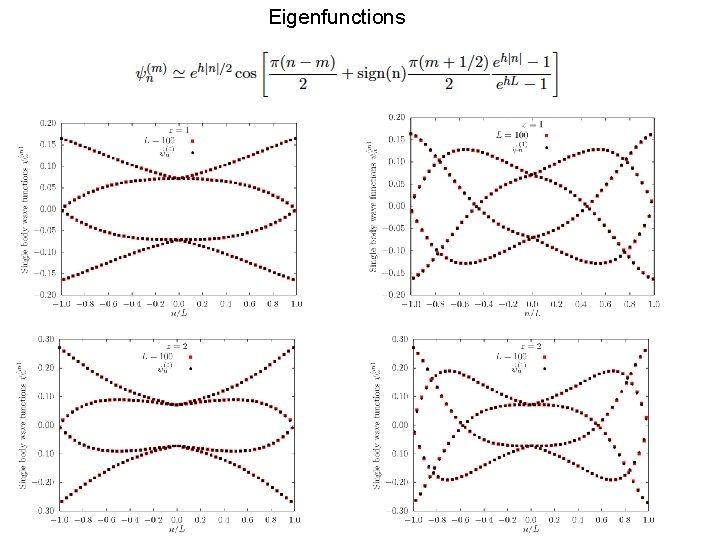
Eigenfunctions

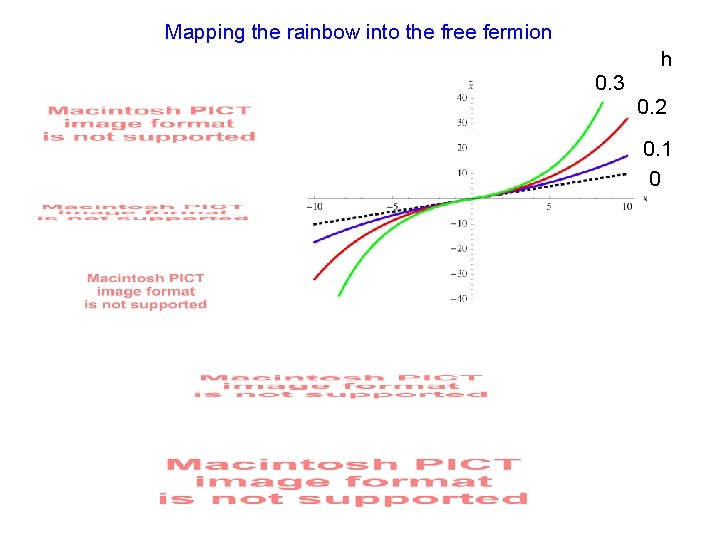
Mapping the rainbow into the free fermion h 0. 3 0. 2 0. 1 0

For x>0 is a conformal map Also for x <0. But it is not conformal in the whole line Periodicity in imaginary time Effective “temperature”

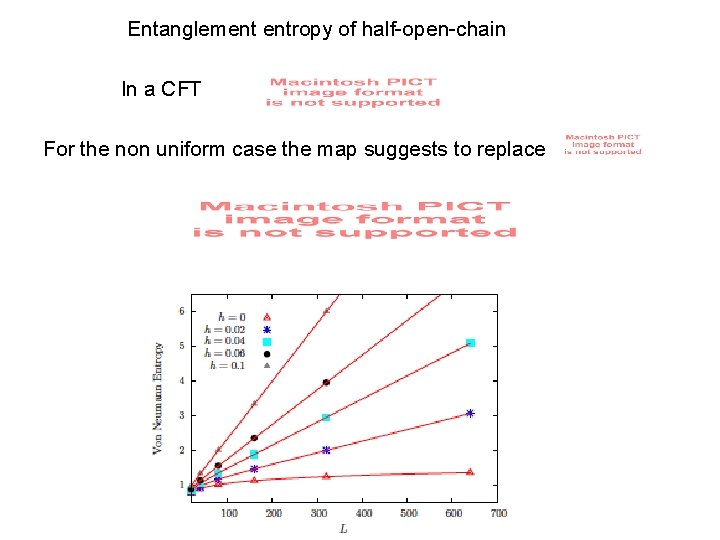
Entanglement entropy of half-open-chain In a CFT For the non uniform case the map suggests to replace

Volumen law as a thermal effect Compare with entropy of a CFT at finite temperature The inhomogeneity coupling h can be seen as “temperature”

Half chain Renyi entropies Free fermion open chain (Fagotti, Calabrese)

Half chain Renyi entropies for the Rainbow In the CFT formula replace

Entanglement Hamiltonian For free fermions Single particle entanglement energies White in the DMRG Cardy, Calabrese, Peschel, … integrable systems Li, Haldane for the FQHE Lepori, De Chiara, Sanpera phase transitions ….

: entanglement energies L=40 L: even L: odd L=41

Entanglement entropy and “level spacing” Approximation This formula is general and can be applied to critical, massive and the rainbow model

Critical model Peschel, Truong (87), Cardy, Peschel (88), Lepori et al (13), Lauchli (14) Corner Transfer Matrix Massive model Cardy, Calabrese (04) using CTM Ercolessi, Evangelisti, Francini, Ravanini 09, … 14 Castro-Alvaredo, Doyon, Levi, Cardy, 07, … 14

Rainbow model with Hamiltonian of a free fermion in a half chain

The GS of the rainbow as a thermofield state Schmidt decomposition where Proof the same for

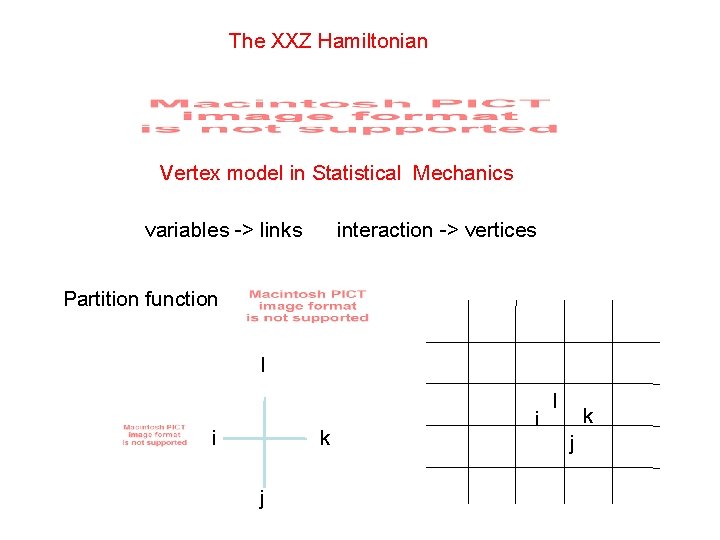
The XXZ Hamiltonian Vertex model in Statistical Mechanics variables -> links interaction -> vertices Partition function l i k j i l k j

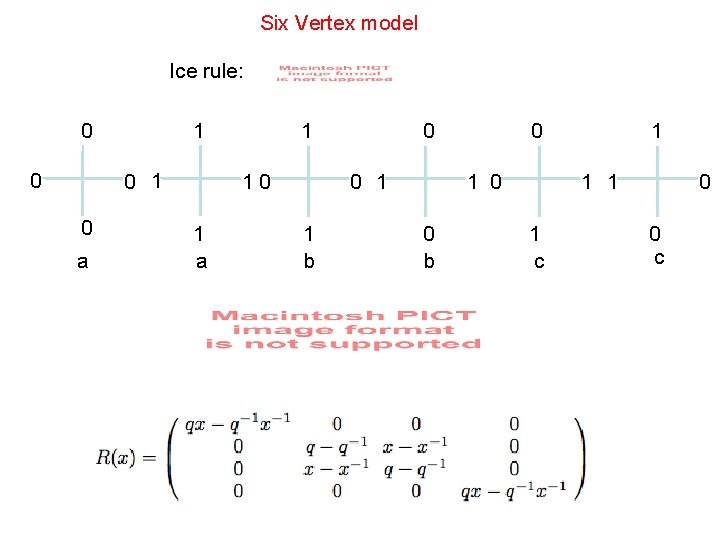
Six Vertex model Ice rule: 0 0 1 0 a 1 10 1 a 0 0 1 1 b 0 1 0 0 b 1 1 c 0 0 c

Bethe ansatz as a Tensor Network Alcaraz, Lazo 2003; Murg, Korepin, Verstraete 2012 1 0 1 0 0 0 0 0

Bethe ansatz as a Tensor Network Alcaraz, Lazo 2003; Murg, Korepin, Verstraete 2012 Homogeneous 1 0 1 0 0 Rapidities 0 0 0 0

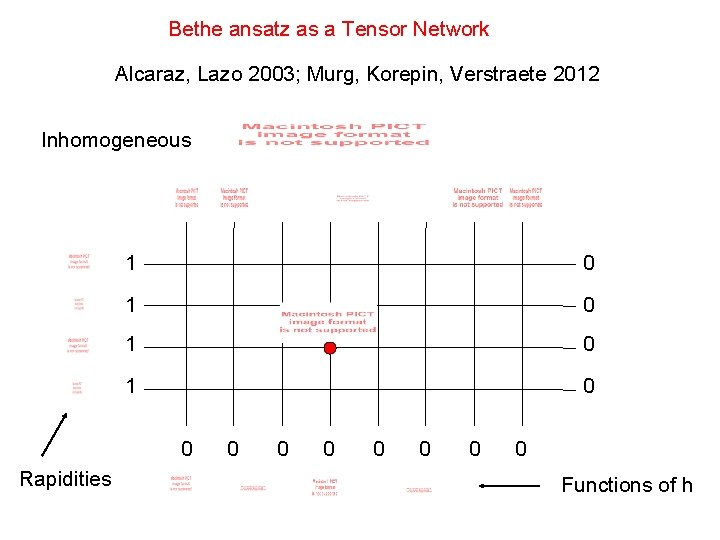
Bethe ansatz as a Tensor Network Alcaraz, Lazo 2003; Murg, Korepin, Verstraete 2012 Inhomogeneous 1 0 1 0 0 Rapidities 0 0 0 0 Functions of h

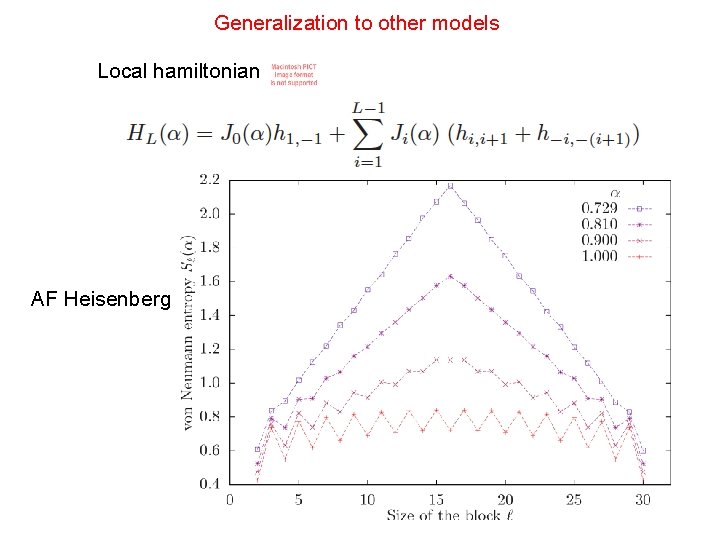
Generalization to other models Local hamiltonian AF Heisenberg

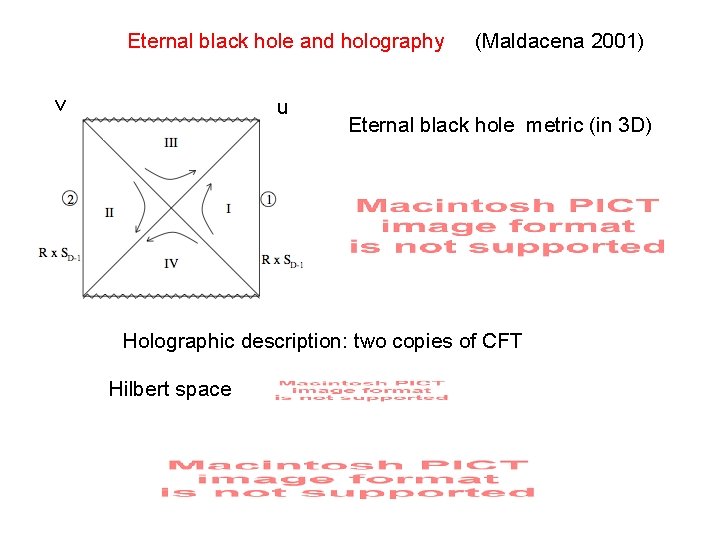
Similarities between the Rainbow and the Unrhu effect A observer with acceleration a detects a thermal bath in the vacuum with temperature The Minkowski vacuum is a thermo-double state

Eternal black hole and holography v u (Maldacena 2001) Eternal black hole metric (in 3 D) Holographic description: two copies of CFT Hilbert space

Generalization to 2 Dimensions

Entropy per length

Local translational invariant Hamiltonians can be turned into Inhomogenous ones whose ground states violate the area law. For strong inhomogeneities the RG explain easily the violations in terms of a valence bond picture For weak inhomogeneities one can construct a field theory that leads to a thermal interpretation of the ground state Analogies with black hole theories: entanglement is related to the space-time geometry.

Thank you Gracias