Fsica Aplicaciones de la dinmica Movimiento de un

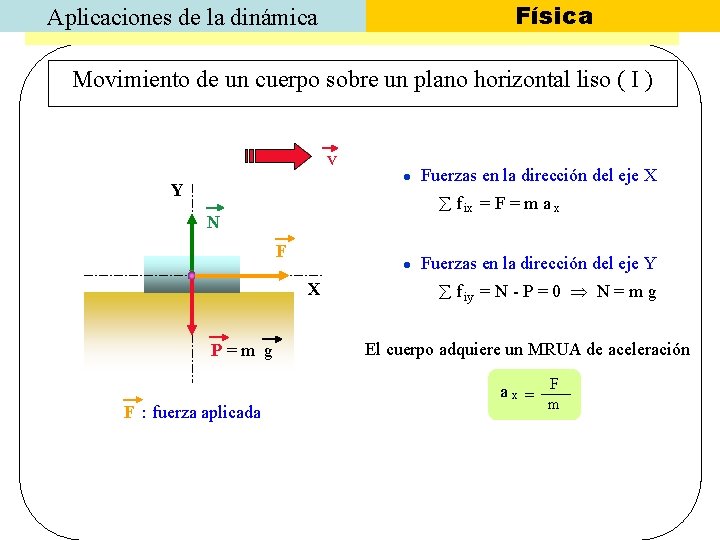
Física Aplicaciones de la dinámica Movimiento de un cuerpo sobre un plano horizontal liso ( I ) v Y f ix = F = m a x N F Fuerzas en la dirección del eje Y X P=m g F : fuerza aplicada Fuerzas en la dirección del eje X f iy = N - P = 0 N = m g El cuerpo adquiere un MRUA de aceleración ax = F m

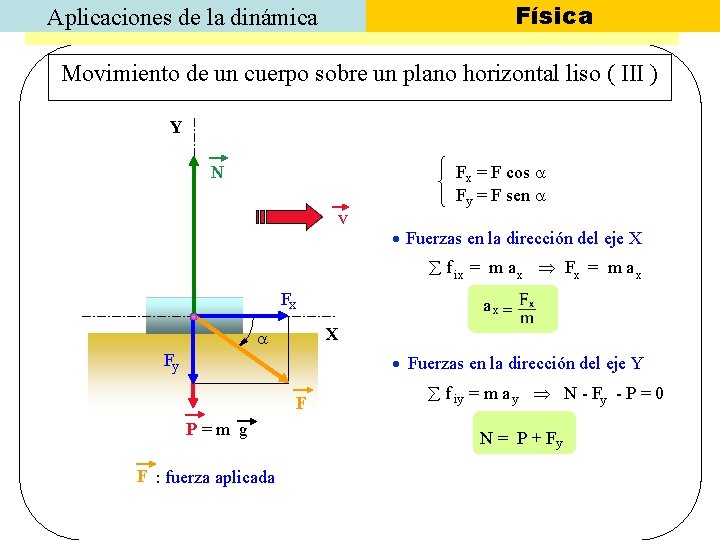
Física Aplicaciones de la dinámica Movimiento de un cuerpo sobre un plano horizontal liso ( III ) Y N v Fx = F cos Fy = F sen Fuerzas en la dirección del eje X f ix = m a x Fx ax = X Fy Fuerzas en la dirección del eje Y F P=m g F : fuerza aplicada f iy = m a y N - Fy - P = 0 N = P + Fy

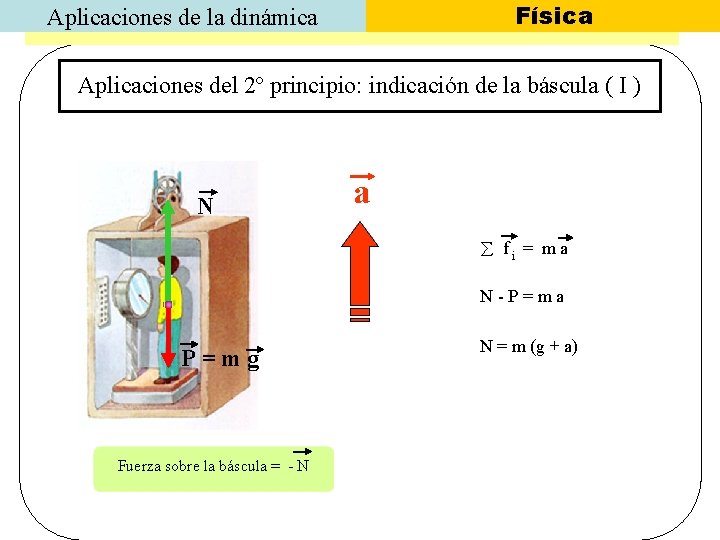
Física Aplicaciones de la dinámica Aplicaciones del 2º principio: indicación de la báscula ( I ) N a fi = m a N-P=ma P=mg Fuerza sobre la báscula = - N N = m (g + a)

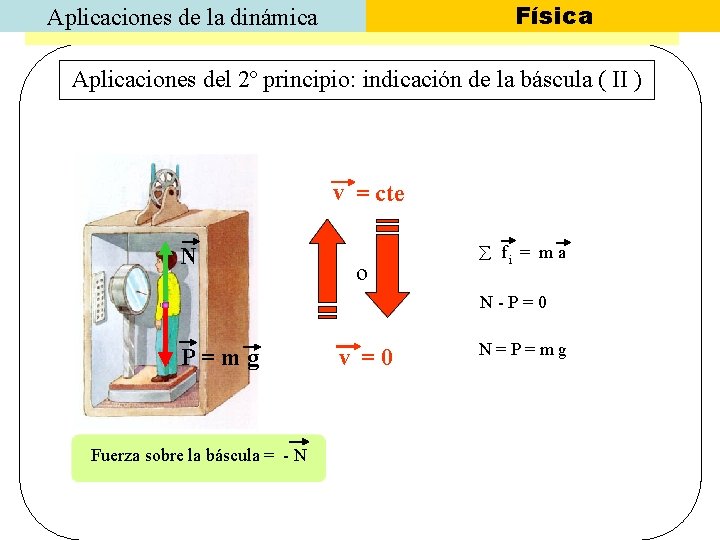
Física Aplicaciones de la dinámica Aplicaciones del 2º principio: indicación de la báscula ( II ) v = cte N o fi = m a N-P=0 P=mg Fuerza sobre la báscula = - N v =0 N=P=mg

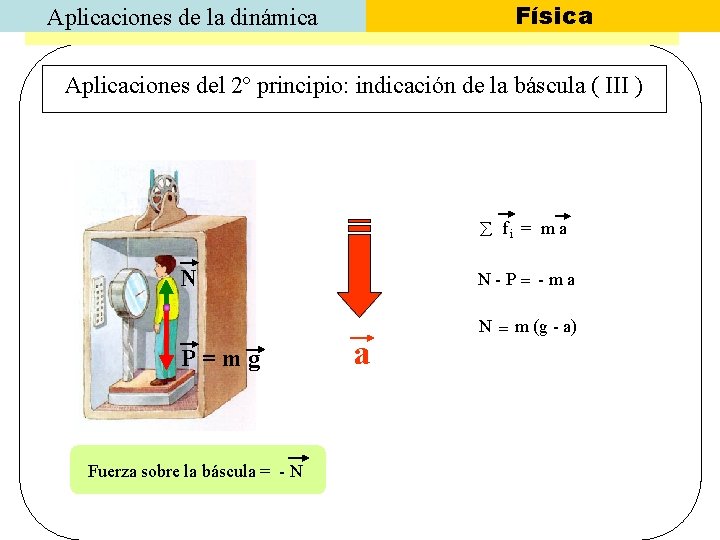
Física Aplicaciones de la dinámica Aplicaciones del 2º principio: indicación de la báscula ( III ) fi = m a N P=mg Fuerza sobre la báscula = - N N-P= -ma a N = m (g - a)

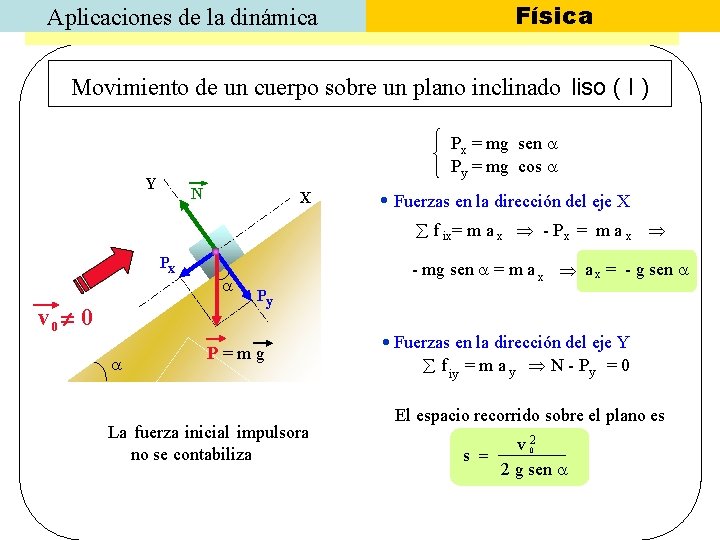
Aplicaciones de la dinámica Física Movimiento de un cuerpo sobre un plano inclinado liso ( I ) Px = mg sen Py = mg cos Y N X Fuerzas en la dirección del eje X f ix= m a x - Px = m a x Px v 0 0 - mg sen = m a x = - g sen Py P=mg La fuerza inicial impulsora no se contabiliza Fuerzas en la dirección del eje Y f iy = m a y N - Py = 0 El espacio recorrido sobre el plano es v 02 s = 2 g sen

Física Aplicaciones de la dinámica Movimiento de un cuerpo sobre un plano inclinado liso ( II ) vo = 0 Px = mg sen Py = mg cos v Y N Px X Fuerzas en la dirección del eje X f ix = m a x - Px = m a x - mg sen = m a x Py P=m g a x = - g sen Fuerzas en la dirección del eje Y f iy = m a y N - Py = 0 N = Py

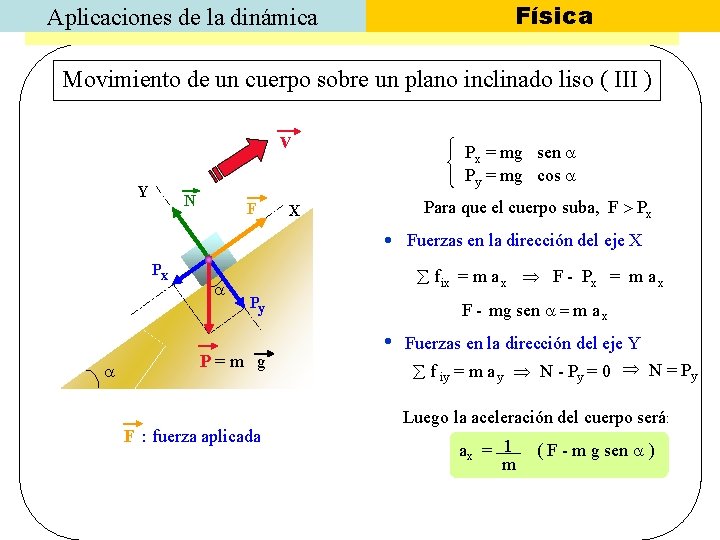
Aplicaciones de la dinámica Física Movimiento de un cuerpo sobre un plano inclinado liso ( III ) v Y N F X Px = mg sen Py = mg cos Para que el cuerpo suba, F Px Fuerzas en la dirección del eje X Px f ix = m a x F - Px = m a x Py P=m g F : fuerza aplicada F - mg sen = m a x Fuerzas en la dirección del eje Y f iy = m a y N - Py = 0 N = Py Luego la aceleración del cuerpo será: ax = 1 m ( F - m g sen )

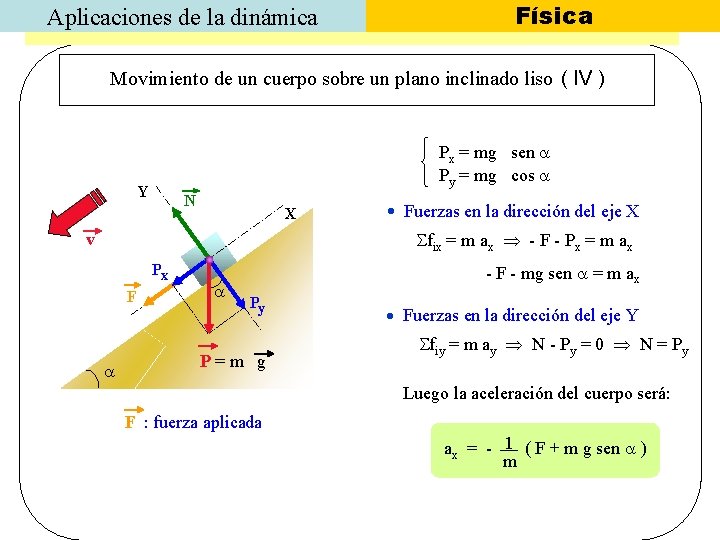
Aplicaciones de la dinámica Física Movimiento de un cuerpo sobre un plano inclinado liso ( IV ) Px = mg sen Py = mg cos Y N X Fuerzas en la dirección del eje X fix = m ax - F - Px = m ax v Px F - F - mg sen = m ax Py P=m g Fuerzas en la dirección del eje Y fiy = m ay N - Py = 0 N = Py Luego la aceleración del cuerpo será: F : fuerza aplicada ax = - 1 ( F + m g sen ) m

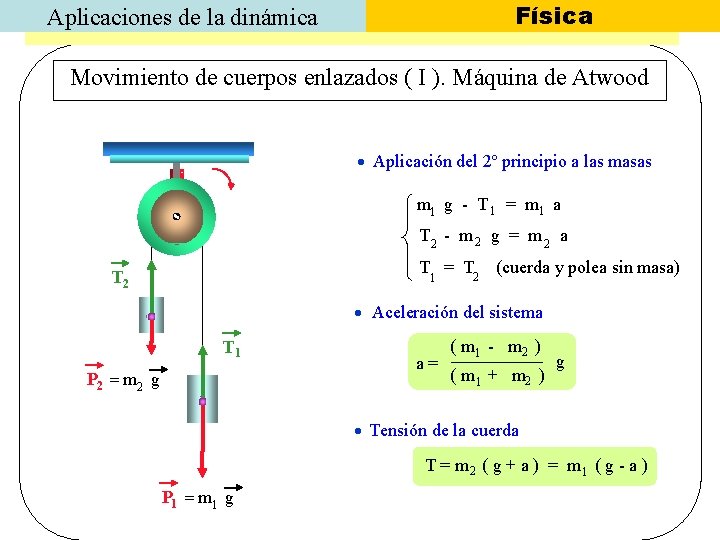
Física Aplicaciones de la dinámica Movimiento de cuerpos enlazados ( I ). Máquina de Atwood Aplicación del 2º principio a las masas m 1 g - T 1 = m 1 a T 2 - m 2 g = m 2 a T = T 2 (cuerda y polea sin masa) T 2 1 Aceleración del sistema T 1 P 2 = m 2 g a= ( m 1 - m 2 ) ( m 1 + m 2 ) g Tensión de la cuerda T = m 2 ( g + a ) = m 1 ( g - a ) P 1 = m 1 g

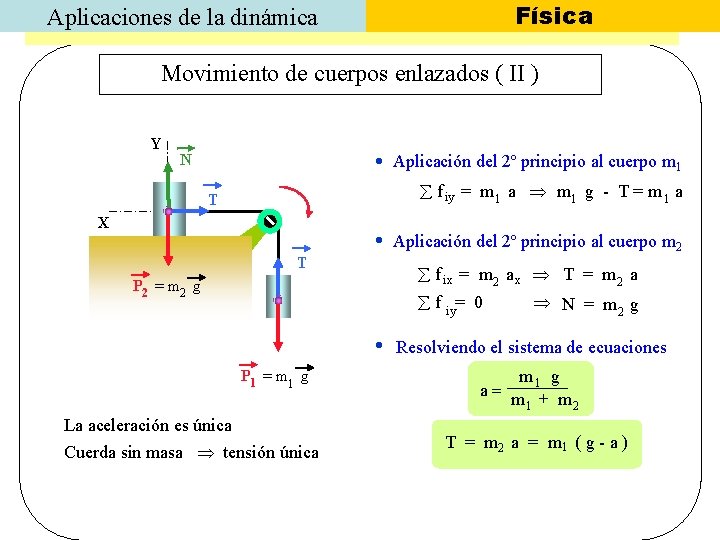
Física Aplicaciones de la dinámica Movimiento de cuerpos enlazados ( II ) Y Aplicación del 2º principio al cuerpo m 1 N f iy = m 1 a m 1 g - T = m 1 a T X T P 2 = m 2 g Aplicación del 2º principio al cuerpo m 2 f ix = m 2 a x T = m 2 a f iy= 0 N = m 2 g Resolviendo el sistema de ecuaciones P 1 = m 1 g La aceleración es única Cuerda sin masa tensión única m 1 g a= m 1 + m 2 T = m 2 a = m 1 ( g - a )

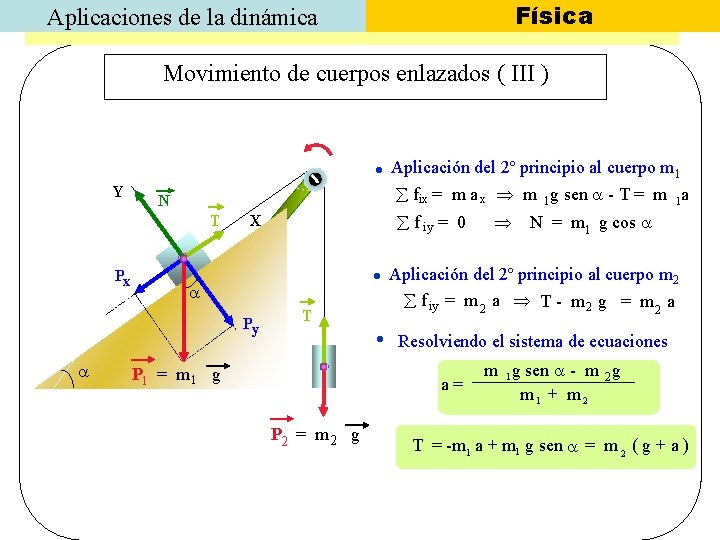
Física Aplicaciones de la dinámica Movimiento de cuerpos enlazados ( III ) Y Aplicación del 2º principio al cuerpo m 1 fix = m a x m 1 g sen - T = m 1 a N T Px Py f iy = 0 X T N = m 1 g cos Aplicación del 2º principio al cuerpo m 2 f iy = m 2 a T - m 2 g = m 2 a Resolviendo el sistema de ecuaciones P 1 = m 1 g a= P 2 = m 2 g m 1 g sen - m 2 g m 1 + m 2 T = -m 1 a + m 1 g sen = m 2 ( g + a )

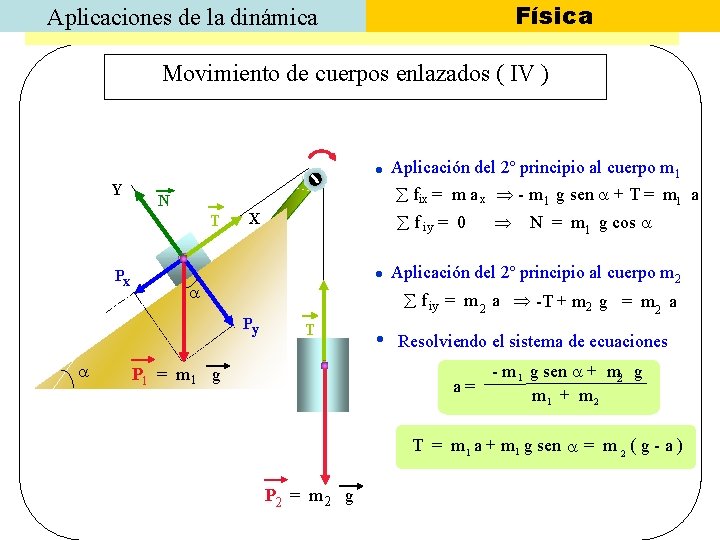
Física Aplicaciones de la dinámica Movimiento de cuerpos enlazados ( IV ) Y Aplicación del 2º principio al cuerpo m 1 fix = m a x - m 1 g sen + T = m 1 a N T Px N = m 1 g cos Aplicación del 2º principio al cuerpo m 2 Py f iy = 0 X f iy = m 2 a -T + m 2 g = m 2 a T P 1 = m 1 g Resolviendo el sistema de ecuaciones a= - m 1 g sen + m 2 g m 1 + m 2 T = m 1 a + m 1 g sen = m 2 ( g - a ) P 2 = m 2 g

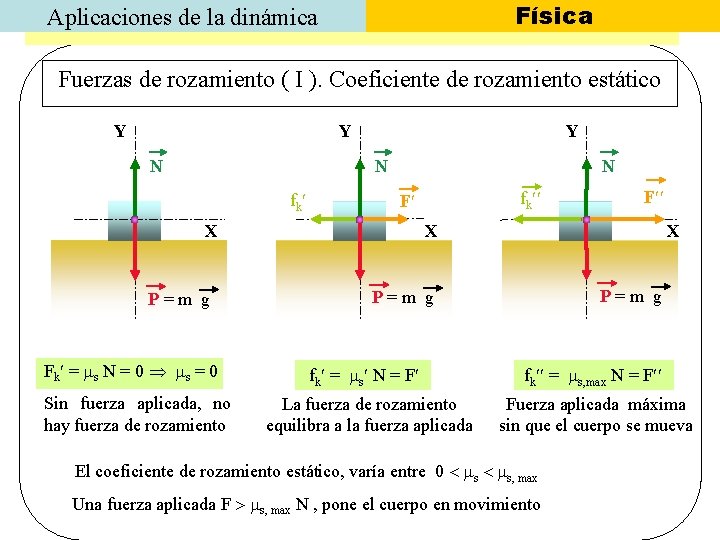
Física Aplicaciones de la dinámica Fuerzas de rozamiento ( I ). Coeficiente de rozamiento estático Y Y N fk N X P=m g Fk = s N = 0 s = 0 Sin fuerza aplicada, no hay fuerza de rozamiento fk F F X X P=m g fk = s N = F fk = s, max N = F La fuerza de rozamiento equilibra a la fuerza aplicada Fuerza aplicada máxima sin que el cuerpo se mueva El coeficiente de rozamiento estático, varía entre 0 s s, max Una fuerza aplicada F s, max N , pone el cuerpo en movimiento

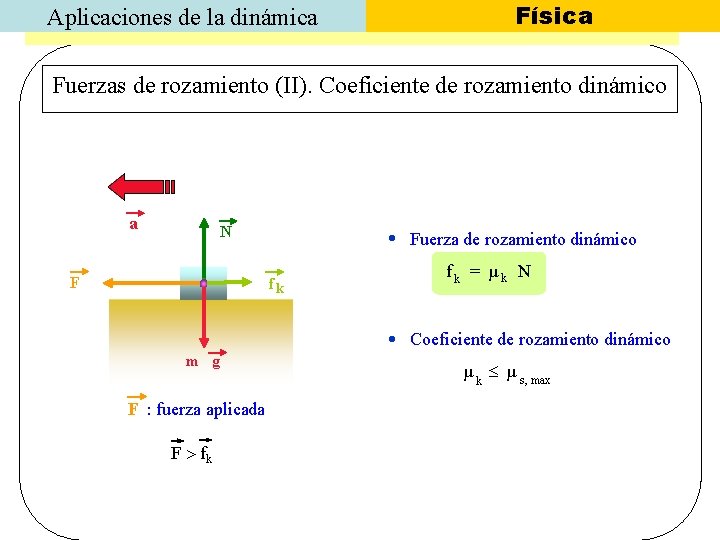
Aplicaciones de la dinámica Física Fuerzas de rozamiento (II). Coeficiente de rozamiento dinámico a N F Fuerza de rozamiento dinámico fk f k = µk N Coeficiente de rozamiento dinámico m g F : fuerza aplicada F fk µ k µ s, max

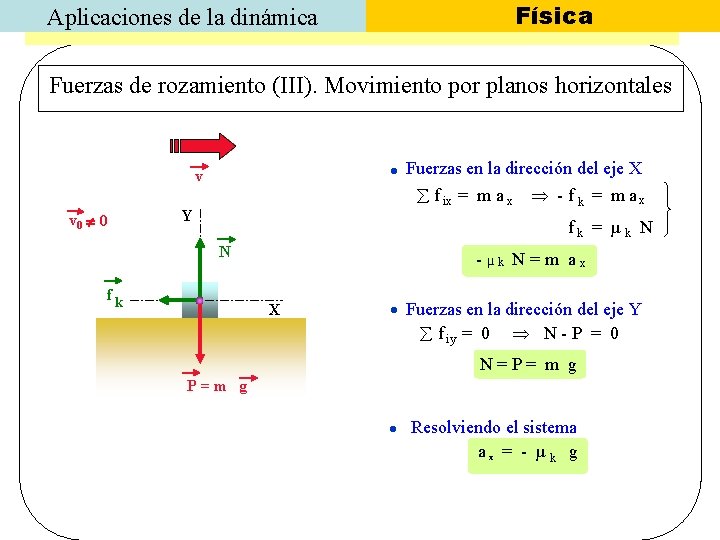
Aplicaciones de la dinámica Física Fuerzas de rozamiento (III). Movimiento por planos horizontales Fuerzas en la dirección del eje X f ix = m a x - f k = m a x v v 0 0 Y fk = µk N N fk - µk N = m a x X Fuerzas en la dirección del eje Y f iy = 0 N - P = 0 N=P= m g P=m g Resolviendo el sistema ax = - µ k g

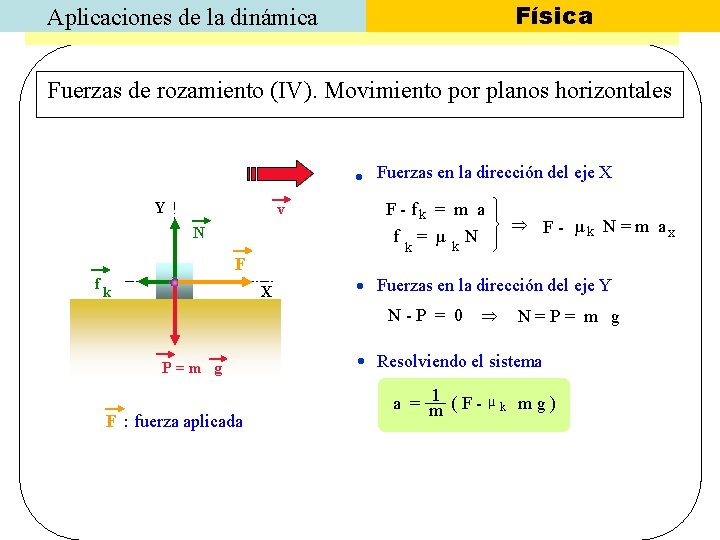
Física Aplicaciones de la dinámica Fuerzas de rozamiento (IV). Movimiento por planos horizontales Fuerzas en la dirección del eje X Y v N F - fk = m a f F fk X k = µ N k F : fuerza aplicada F - µ k N = m ax Fuerzas en la dirección del eje Y N-P = 0 P=m g N=P= m g Resolviendo el sistema 1 (F-µ mg) a = m k

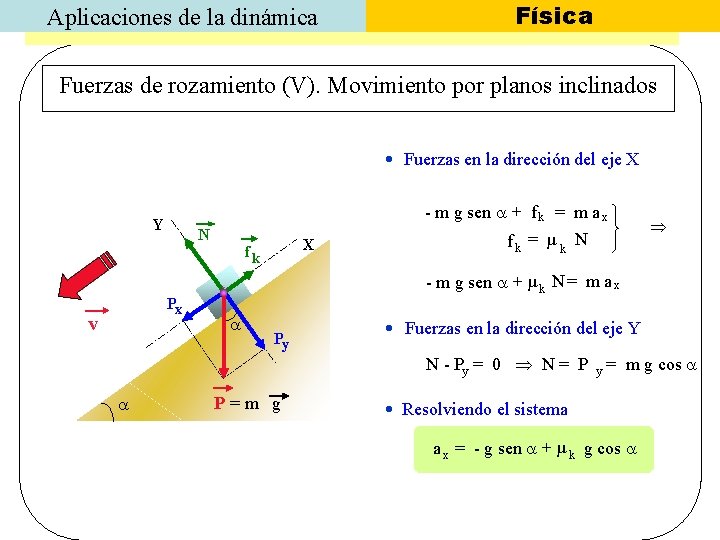
Aplicaciones de la dinámica Física Fuerzas de rozamiento (V). Movimiento por planos inclinados Fuerzas en la dirección del eje X - m g sen + f k = m a x Y N Px v X fk fk = µ k N - m g sen + µ k N = m a x Py Fuerzas en la dirección del eje Y N - Py = 0 N = P P=m g y = m g cos Resolviendo el sistema a x = - g sen + µ k g cos

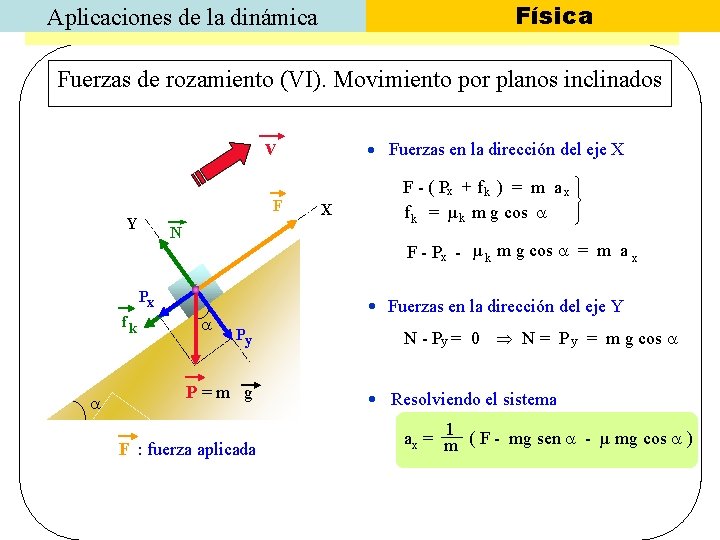
Física Aplicaciones de la dinámica Fuerzas de rozamiento (VI). Movimiento por planos inclinados v F Y N X F - ( Px + f k ) = m a x f k = µ k m g cos F - Px - µ k m g cos = m a x Px fk Fuerzas en la dirección del eje X Fuerzas en la dirección del eje Y Py P=m g F : fuerza aplicada N - Py = 0 N = P y = m g cos Resolviendo el sistema 1 ( F - mg sen - µ mg cos ) ax = m

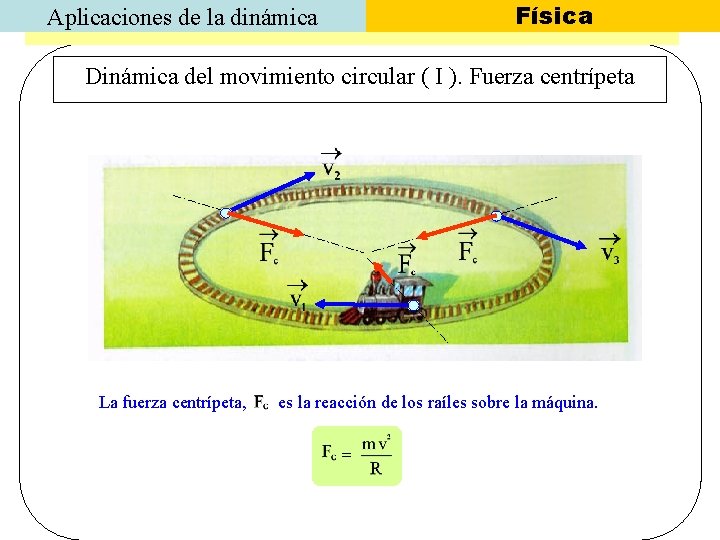
Física Aplicaciones de la dinámica Dinámica del movimiento circular ( I ). Fuerza centrípeta La fuerza centrípeta, es la reacción de los raíles sobre la máquina. =

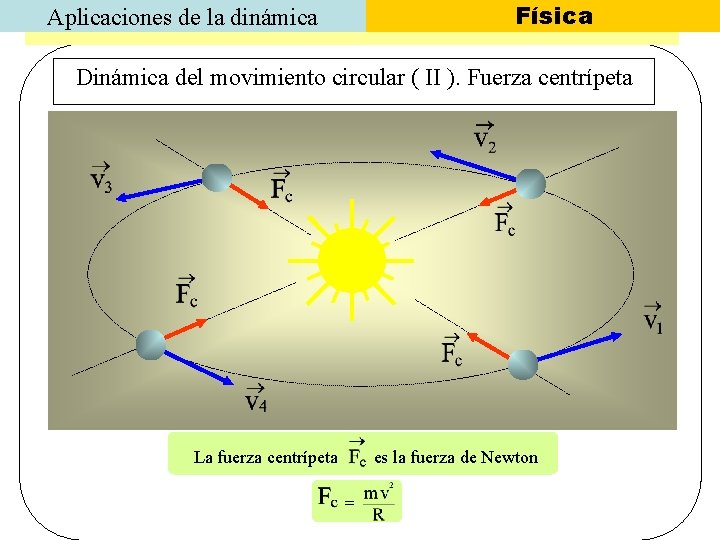
Física Aplicaciones de la dinámica Dinámica del movimiento circular ( II ). Fuerza centrípeta La fuerza centrípeta es la fuerza de Newton =

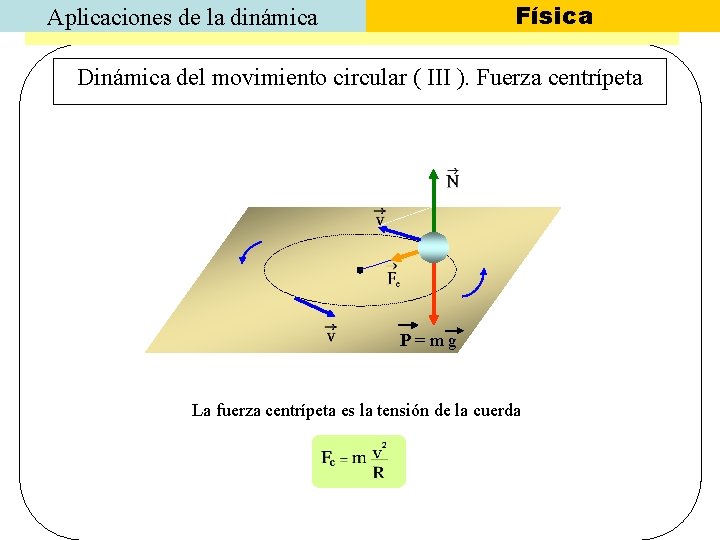
Física Aplicaciones de la dinámica Dinámica del movimiento circular ( III ). Fuerza centrípeta P=mg La fuerza centrípeta es la tensión de la cuerda

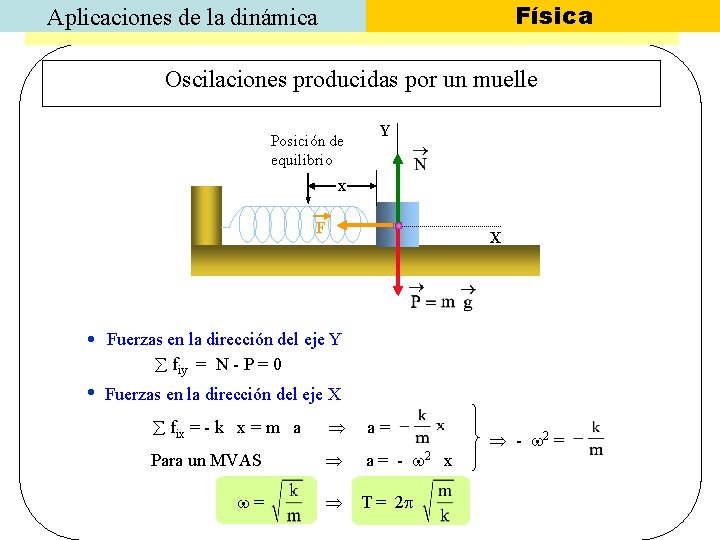
Física Aplicaciones de la dinámica Oscilaciones producidas por un muelle Posición de equilibrio Y x F X Fuerzas en la dirección del eje Y fiy = N - P = 0 Fuerzas en la dirección del eje X fix = - k x = m a a= Para un MVAS a = - 2 x = T = 2 - 2 =