FirstOrder Logic Knowledge Interchange Format KIF Professor Richard

First-Order Logic Knowledge Interchange Format (KIF) Professor Richard Fikes CS 222 Winter 2001 Computer Science Department Stanford University 1/17/01 1 Knowledge Systems Laboratory, Stanford University

KR Language Components u A logical formalism ä Syntax for wffs ä Vocabulary of logical symbols (e. g. , AND, OR, NOT, =>, <=>) ä Interpretation semantics for the logical symbols E. g. , “(=> A B)” is true if and only if B is true or A is false. u An ontology ä Vocabulary of non-logical symbols > Relations, functions, constants ä Definitions of non-primitive symbols E. g. , (<=> (Bachelor ? x) (AND (Man ? x) (Unmarried ? x))) ä Axioms restricting the interpretations of primitive symbols E. g. , (=> (Person ? x) (Gender (Mother ? x) Female)) u A proof theory ä Specification of the reasoning steps that are logically sound E. g. , From “(=> S 1 S 2)” and “S 1”, conclude “S 2”. 2 Knowledge Systems Laboratory, Stanford University

Interlingua for Multi-Use Knowledge Language 1 . . . Language 2 Language n KIF KB Library u Knowledge Interchange Format (KIF) ä First order predicate logic ä Includes numbers, lists, and strings ä Linear ASCII syntax ä In the process of becoming an ANSI standard 3 Knowledge Systems Laboratory, Stanford University

Conceptualization u Set of objects about which knowledge is being expressed ä Universe of discourse ä Objects can be – > > > Concrete Abstract Primitive Composite Fictional Clyde, my car Justice, 2 Resister Electric circuit Sherlock Holmes ä Objects always in the conceptualization (i. e. , in the ontology) > > > u 4 Real and complex numbers All finite lists of objects Words ASCII characters Finite strings of ASCII characters ^ (bottom) Set of relations and functions on the objects Knowledge Systems Laboratory, Stanford University

Conceptualization u Set of objects about which knowledge is being expressed ä Universe of discourse u Set of relations and functions on the objects ä Relation > Set of finite lists of objects E. g. , Parent: {(Richard Earl) (Richard Polly) (Debbie Don) … } > Mapping: <list of objects> ® <truth value> ä Function > Relation that has a unique nth element for a given n-1 elements E. g, +: {(1 3 4) (17 23 40) (2 7 10 12 31) …} > Referred to as (arg 1, arg 2, … , argk, value) > Mapping: <list of objects> ® <object> 5 Knowledge Systems Laboratory, Stanford University

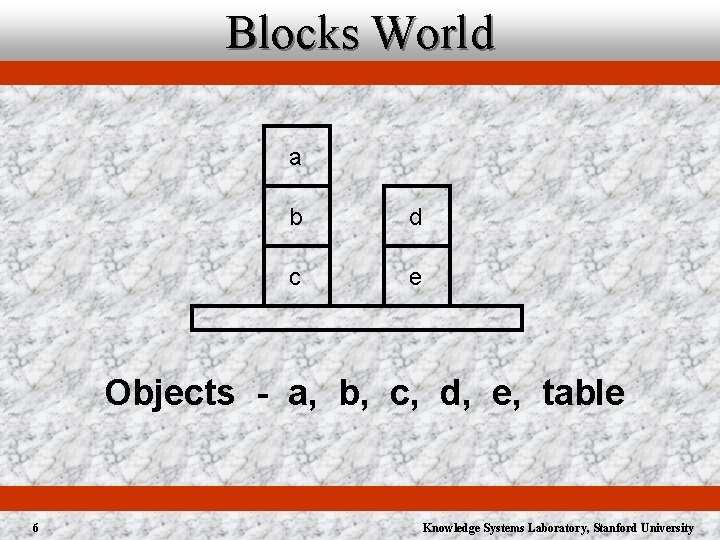
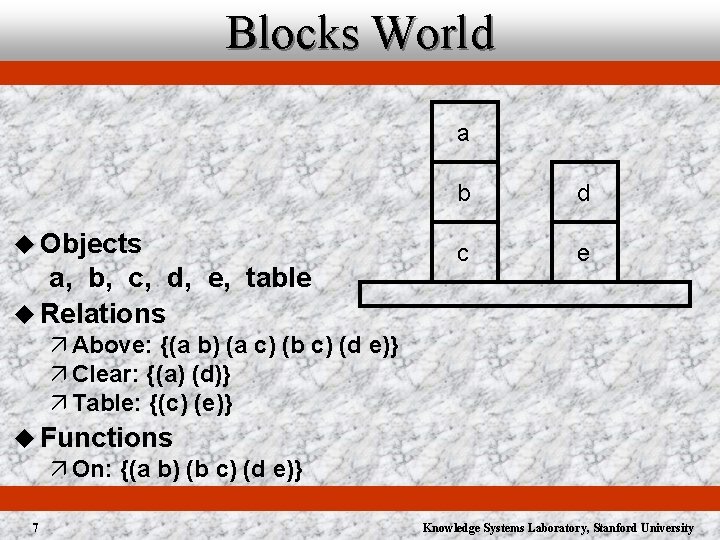
Blocks World a b d c e Objects - a, b, c, d, e, table 6 Knowledge Systems Laboratory, Stanford University

Blocks World a u Objects a, b, c, d, e, table u Relations b d c e ä Above: {(a b) (a c) (b c) (d e)} ä Clear: {(a) (d)} ä Table: {(c) (e)} u Functions ä On: {(a b) (b c) (d e)} 7 Knowledge Systems Laboratory, Stanford University

KBs, Sentences, Terms, Words u Knowledge Base – Collection of sentences u Sentence – Expression denoting a statement u Term – Expression denoting an object u Words ä Constant > Word not beginning with “? ” or “@” E. g. , Fred, Block-A, Justice ä Individual Variable > Word beginning with “? ” E. g, ? x, ? The-First-Murderer ä Sequence Variable > Word beginning with “@” E. g, @x, @The-Other-Murderers 8 Knowledge Systems Laboratory, Stanford University

Function Terms and Relational Sentences u Function Term ä (<function constant> <term>* [<sequence variable>]) E. g. , (plus 2 3) (Father-Of Richard) (plus 4 ? x @Other-Addends) u Relational Sentence ä (<relation constant> <term>* [<sequence variable>]) E. g, (Parent Richard Earl) (Clear A) (Set-Partition Set 1 @Sets) ä Equations – (= <term>) E. g, (= (Father Richard) Earl) (= A B) ä Inequalities – (/= <term>) E. g, (/= (Father Richard) (Father Bob)) (/= A B) 9 Knowledge Systems Laboratory, Stanford University

Declarative Semantics u Interpretation of a constant – ä ä u <object constant> Þ <object> <logical constant> Þ <truth value> <relation constant> Þ <relation> <function constant> Þ <function> Variable assignment – ä <individual variable> Þ <object> ä <sequence variable> Þ <finite sequence of objects> u Semantic value of a term – <term> Þ <object> ä Defined in terms of an interpretation and variable assignment u Truth value of a sentence – <sentence> Þ {true, false} ä Defined in terms of an interpretation and variable assignment u 10 Version of a variable assignment Knowledge Systems Laboratory, Stanford University

Semantic Value u Denote “semantic value” by “SIV” ä I is an interpretation ä V is a variable assignment u Semantic value of a constant ä SIV(<constant>) = I(<constant>) u Semantic value of a variable ä SIV(<variable>) = V(<variable>) u Semantic value of a function term ä SIV((fn term 1 … termn)) = The object O such that áSIV(term 1) … SIV (termn) Oñ is a member of set I(fn) ä SIV((fn term 1 … termn @var)) = The object O such that áSIV(term 1) … SIV(termn) | V(@var) Oñ is a member of set I(fn) 11 Knowledge Systems Laboratory, Stanford University

Truth Value u Denote “truth value” by “TIV” ä I is an interpretation ä V is a variable assignment u Logical constants ä Tiv(<constant>) = I(<constant>) ä Tiv(true) = true ä Tiv(false) = false u Truth value of a relational sentence ä TIV((rel term 1 … termn)) = > true when áSIV(term 1), … , SIV (termn)ñ is a member of set I(rel) > false otherwise ä TIV((rel term 1 … termn @var)) = > true when áSIV (term 1), … , SIV (termn) | SIV (@var)ñ is a member of set I(rel) > false otherwise 12 Knowledge Systems Laboratory, Stanford University

Equations and Inequalities u Equations ä TIV((= term 1 term 2)) = > true when SIV(term 1) and SIV(term 2) are the same object > false otherwise u Inequalities ä TIV((/= term 1 term 2)) = TIV((not (= term 1 term 2))) 13 Knowledge Systems Laboratory, Stanford University

Logical Sentences: not, and, or u Negation – (not <sentence>) E. g. , (not (On A D)) (not (On B B)) ä TIV((not sent)) = > true when TIV(sent) is false > false otherwise u Conjunction – (and <sentence>*) E. g. , (and (On A B) (On B C)) ä TIV((and sent 1 … sentn)) = > true when TIV(senti) is true for all I = 1, … , n > false otherwise u Disjunction – (or <sentence>*) E. g. , (or (On A D) (On A B)) ä TIV((or sent 1 … sentn)) = > true when TIV(senti) is true for some I = 1, … , n > false otherwise 14 Knowledge Systems Laboratory, Stanford University

Logical Sentences: => <= <=> u Implication – (=> <sentence>* <sentence>) E. g. , (=> (On A B) (On B C)) ä TIV((=> ante 1 … anten conse)) = > true when: – TIV(antei) is false for some I = 1, … , n; or – TIV (conse) is true > false otherwise E. g. , (=> (On A D) (On D D)) ä TIV((=> a 1 … an c)) = TIV ((or (not a 1) … (not an) c)) u Implication – (<= <sentence>*) u Logical equivalence – (<=> <sentence>) ä TIV ((sent 1 <=> sent 2)) = > true when TIV (sent 1) = TIV (sent 2) > false otherwise ä TIV((<=> s 1 s 2)) = TIV((and (=> s 1 s 2) (=> s 2 s 1))) 15 Knowledge Systems Laboratory, Stanford University

Logical Terms u (if <sentence> <term> [<term>]) E. g, (if (Above A B) ä SIV((if sent term)) = > SIV(term) when TIV(sent) = true > ^ otherwise ä SIV((if sent term 1 term 2)) = > SIV(term 1) when TIV(sent) = true > SIV(term 2) otherwise u (cond (<sentence> <term>) … (<sentence> <term>)) E. g. , (cond ((Above A B) A) ((Above B A) B)) ä SIV((cond (sent 1 term 1) … (sentn termn))) = > SIV(term 1) when TIV(sent 1) = true. . . > SIV(termn) when TIV(sentn) = true > ^ otherwise 16 Knowledge Systems Laboratory, Stanford University

Declarative Semantics u Interpretation of a constant – ä ä u <object constant> Þ <object> <logical constant> Þ <truth value> <relation constant> Þ <relation> <function constant> Þ <function> Variable assignment – ä <individual variable> Þ <object> ä <sequence variable> Þ <finite sequence of objects> u Semantic value of a term – <term> Þ <object> ä Defined in terms of an interpretation and variable assignment u Truth value of a sentence – <sentence> Þ {true, false} ä Defined in terms of an interpretation and variable assignment u Version of a variable assignment V’ is a version of a variable assignment V with respect to variables v 1, …, vn if and only if V’ agrees with V on all variables except v 1, …, vn. 17 Knowledge Systems Laboratory, Stanford University

Universally Quantified Sentences u (forall <individual variable> <sentence>) E. g, (forall ? b (not (On ? b))) ä TIV((forall ? var sent)) = > true when TIV’(sent) = true for all versions V’ of V with respect to variable ? var > false otherwise u (forall (<individual variable>*) <sentence>) E. g. , (forall (? b 1 ? b 2) (=> (On ? b 1 ? b 2) (Above ? b 1 ? b 2))) ä TIV ((forall (? var 1 … ? varn) sent)) = > true when TIV’(sent) = true for all versions V’ of V with respect to ? var 1 … ? varn > false otherwise 18 Knowledge Systems Laboratory, Stanford University

Existentially Quantified Sentences u (exists <individual variable> <sentence>) E. g, (forall ? b 1 (or (on ? b 1 table) (exists ? b 2 (On ? b 1 ? b 2)))) ä TIV((exists ? var sent)) = > true when TIV’(sent) = true for some version V’ of V with respect to variable ? var > false otherwise u (exists (<individual variable>*) <sentence>) E. g. , (exists (? b 1 ? b 2) (and (On ? b 1 ? A) (Above ? A ? b 2))) ä TIV ((exists (? var 1 … ? varn) sent)) = > true when TIV’(sent) = true for some version V’ of V with respect to ? var 1 … ? varn > false otherwise u forall not in the scope of an exists may be omitted E. g, (or (on ? b 1 table) (exists ? b 2 (On ? b 1 ? b 2))) 19 Knowledge Systems Laboratory, Stanford University

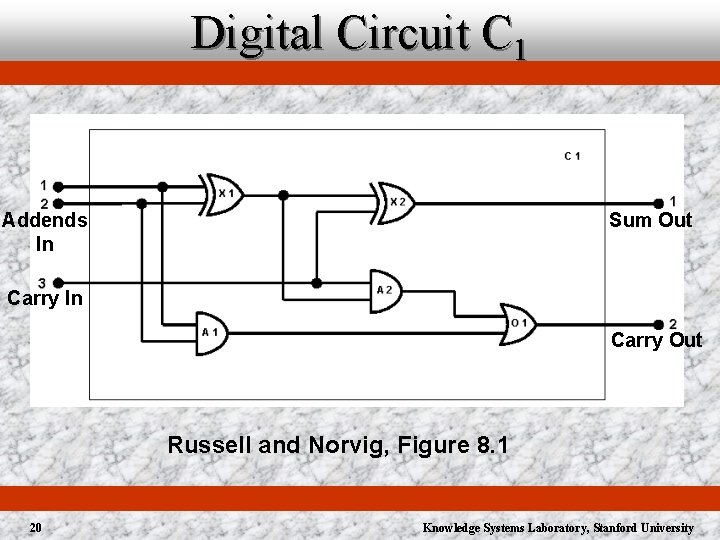
Digital Circuit C 1 Addends In Sum Out Carry In Carry Out Russell and Norvig, Figure 8. 1 20 Knowledge Systems Laboratory, Stanford University

Domain Conceptualization u Objects ä ä ä u Circuits Terminals Signals Gate types Signal values Relations ä Connected: (<terminal>) u Functions ä ä 21 Type: <gate> ® <gate type> In: (<index> <gate>) ® <input terminal> Out: (<index> <gate>) ® <output terminal> Signal: <terminal> ® <signal value> Knowledge Systems Laboratory, Stanford University

Electronic Circuit Domain Theory u Connected terminals have the same signal (=> (Connected ? t 1 ? t 2) (Signal ? t 1 (Signal ? t 2))) (=> (Connected ? t 1 ? t 2) (= (Signal ? t 1) (Signal ? t 2))) u Signal at terminal is either on or off (or (Signal ? t On) (Signal ? t Off)) (not (= On Off)) u Connected is commutative (<=> (Connected ? t 1 ? t 2) (Connected ? t 2 ? t 1)) 22 Knowledge Systems Laboratory, Stanford University

OR and AND Gates u OR gate’s output is on when any of its inputs are on (=> (Type ? g OR) (<=> (Signal (Out 1 ? g) On) (exists ? i (Signal (In ? i ? g) On)))) u AND gate’s output is off when any of its inputs are off (=> (Type ? g AND) (<=> (Signal (Out 1 ? g) Off) (exists ? i (Signal (In ? i ? g) Off)))) 23 Knowledge Systems Laboratory, Stanford University

XOR and NOT Gates u XOR gate’s output is on when its inputs are different (=> (Type ? g XOR) (<=> (Signal (Out 1 ? g) On) (not (Signal (In 1 ? g) (Signal (In 2 ? g)))))) u NOT gate’s output is different from its inputs (=> (Type ? g NOT) (not (Signal (Out 1 ? g) (Signal (In 1 ? g))))) 24 Knowledge Systems Laboratory, Stanford University

Circuit C 1 Representation u Gates (Type X 1 XOR) (Type A 1 AND) (Type O 1 OR) u (Type X 2 XOR) (Type A 2 AND) Connections (Connected (Out 1 X 1) (In 1 X 2)) (Connected (Out 1 X 1) (In 2 A 2)) (Connected (Out 1 A 2) (In 1 O 1)) (Connected (Out 1 A 1) (In 2 O 1)) (Connected (Out 1 X 2) (Out 1 C 1)) (Connected (Out 1 O 1) (Out 2 C 1)) 25 (Connected (In 1 C 1) (In 1 X 1)) (Connected (In 1 C 1) (In 1 A 1)) (Connected (In 2 C 1) (In 2 X 1)) (Connected (In 2 C 1) (In 2 A 1)) (Connected (In 3 C 1) (In 2 X 2)) (Connected (In 3 C 1) (In 1 A 2)) Knowledge Systems Laboratory, Stanford University