Financial Programming An Introduction Thorvaldur Gylfason Outline q

Financial Programming An Introduction Thorvaldur Gylfason

Outline q Monetary approach to balance of payments q Accounting relationships üTrace linkages among o Balance of payments accounts o National income accounts o Fiscal accounts o Monetary accounts üProceed from linkages to financial programming q Analytical model üFinancial programming in action

What is money? 1 1. Liabilities of banking system to the public 1. That is, the private sector and public enterprises 2. M = C + T 1. C = currency, T = deposits 3. The broader the definition of deposits. . . 1. Demand deposits, time and savings deposits, etc. , 4. . the broader the corresponding definition of money

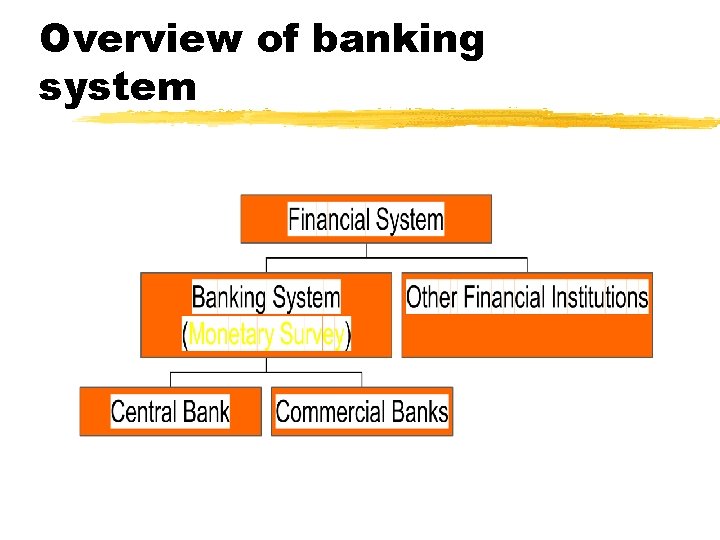
Overview of banking system

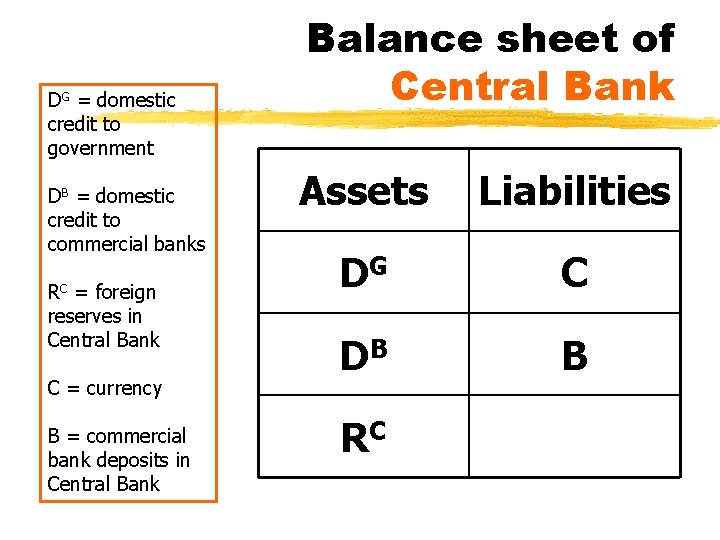
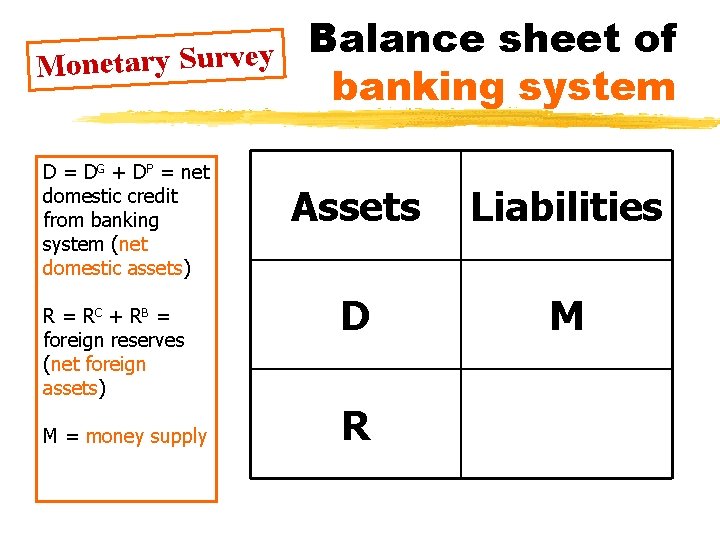
DG = domestic credit to government DB = domestic credit to commercial banks RC = foreign reserves in Central Bank C = currency B = commercial bank deposits in Central Bank Balance sheet of Central Bank Assets Liabilities DG C DB B RC

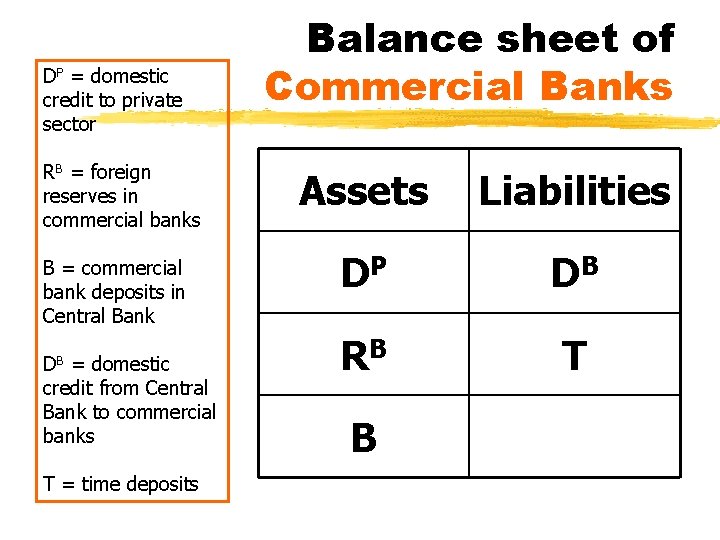
DP = domestic credit to private sector RB = foreign reserves in commercial banks B = commercial bank deposits in Central Bank DB = domestic credit from Central Bank to commercial banks T = time deposits Balance sheet of Commercial Banks Assets Liabilities DP DB RB T B

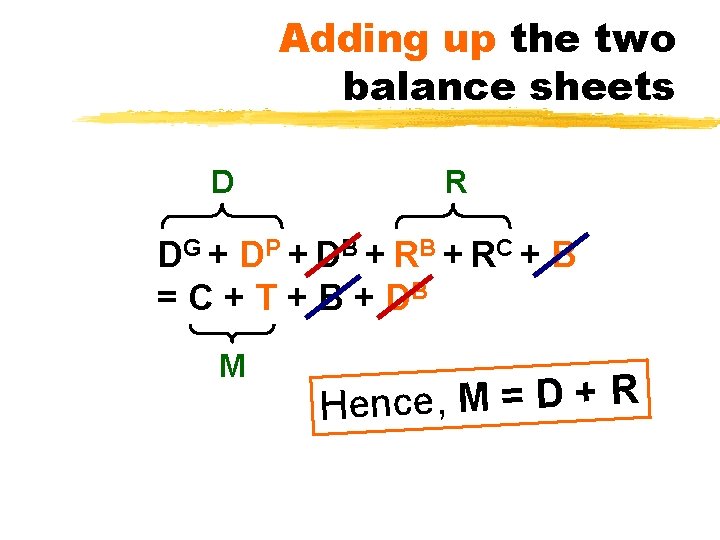
Adding up the two balance sheets D R DG + DP + DB + RC + B = C + T + B + DB M Hence, M = D + R

Monetary Survey D = DG + DP = net domestic credit from banking system (net domestic assets) R = RC + RB = foreign reserves (net foreign assets) M = money supply Balance sheet of banking system Assets Liabilities D M R

A fresh view of money The monetary survey implies the following new definition of money: M=D+R where M is broad money (M 2), which equals narrow money (M 1) + quasi-money q One of the most useful equations in economics q Money is, by definition, equal to the sum of domestic credit from the banking system (net domestic assets) and foreign exchange reserves in the banking system (net foreign assets).

An alternative derivation of monetary survey q Public sector ü G – T = B + DG + DF q Private sector ü I – S = DP - M - B q External sector ü X – Z = R - DF Now, add them up

An alternative derivation of monetary survey q Public sector ü G – T = B + DG + DF q Private sector ü I – S = DP - M - B q External sector ü X – Z = R - DF o s , 0 = Z – X + S G–T+I– o r e z o t m u s s e id s left-hand

An alternative derivation of monetary survey q Public sector ü G – T = B + DG + DF q Private sector ü I – S = DP - M - B q External sector ü X – Z = R - DF

An alternative derivation of monetary survey q Public sector ü G – T = B + DG + DF q Private sector ü I – S = DP - M - B q External sector ü X – Z = R - DF

An alternative derivation of monetary survey q Public sector ü G – T = B + DG + DF q Private sector ü I – S = DP - M - B q External sector ü X – Z = R - DF

An alternative derivation of monetary survey q Public sector ü G – T = B + DG + DF q Private sector ü I – S = DP - M - B q External sector ü X – Z = R - DF

An alternative derivation of monetary survey ence, q Public sector H M=D+R ü G – T = B + DG + DF q Private sector ü I – S = DP - M - B q External sector ü X – Z = R - DF So, adding them up, we get: 0 = D - M + R because DG + DP = D

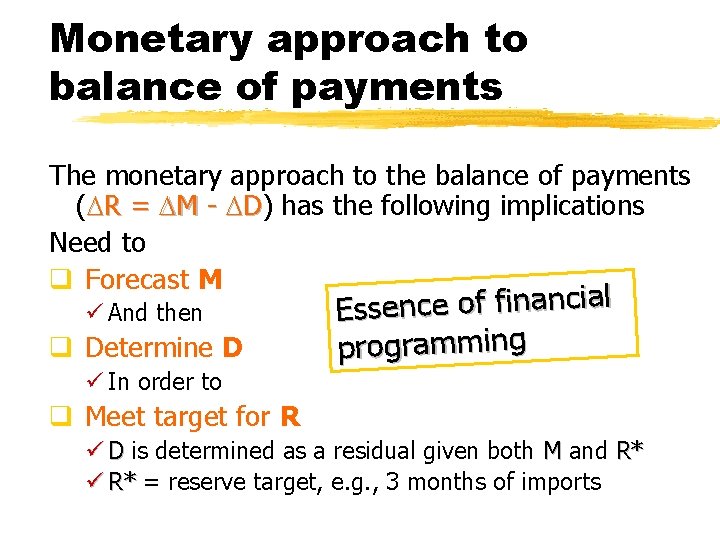
Monetary approach to balance of payments The monetary survey (M = D + R) R has three key implications: q Money is endogenous ü If R increases, then M increases ü Important in open economies q Domestic credit affects money ü If R increases, may want to reduce D to contain M q R = M - D ü Here R = X – Z + F ü Monetary approach to balance of payments

Monetary approach to balance of payments The monetary approach to the balance of payments ( R = M - D) has the following implications Need to q Forecast M ü And then q Determine D ü In order to l ia c n a in f f o e c n e s s E programming q Meet target for R ü D is determined as a residual given both M and R* ü R* = reserve target, e. g. , 3 months of imports

Monetary approach to balance of payments q Domestic credit is a policy variable that involves both monetary and fiscal policy q Can reduce* domestic credit (D) üTo private sector *Or slow down üTo public sector • By reducing government spending • By increasing taxes q Monetary and fiscal policy are closely related through domestic credit

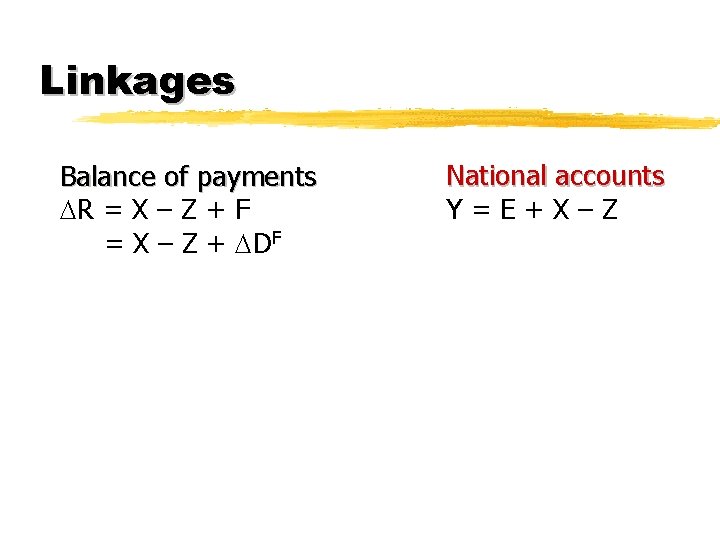
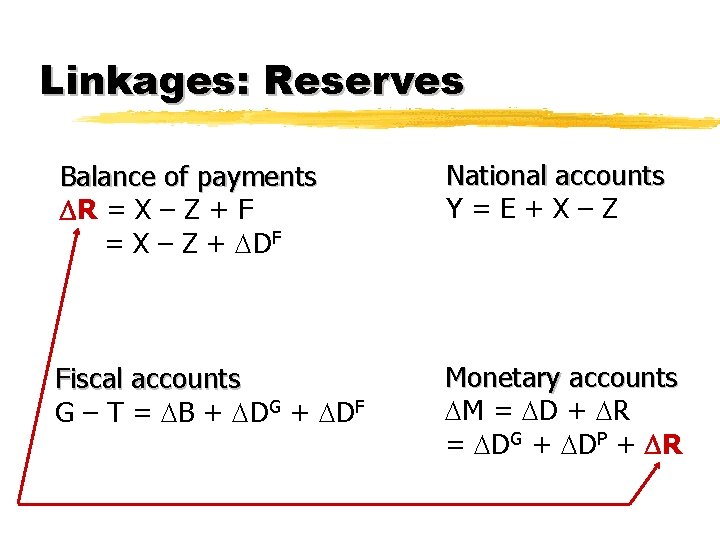
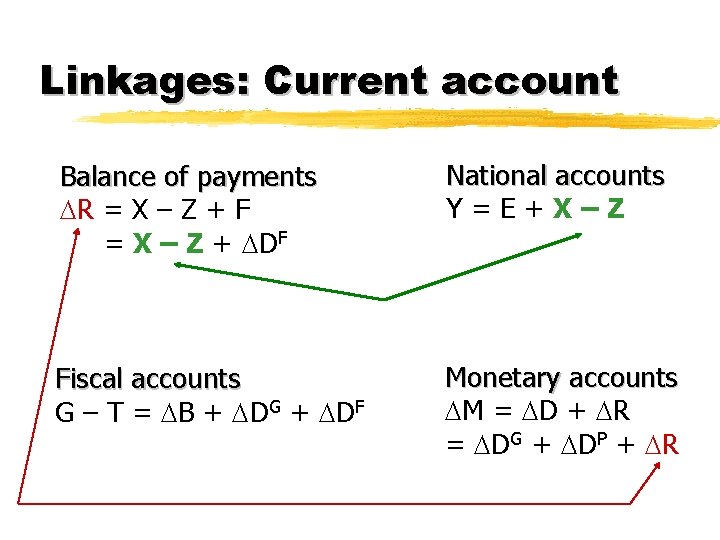
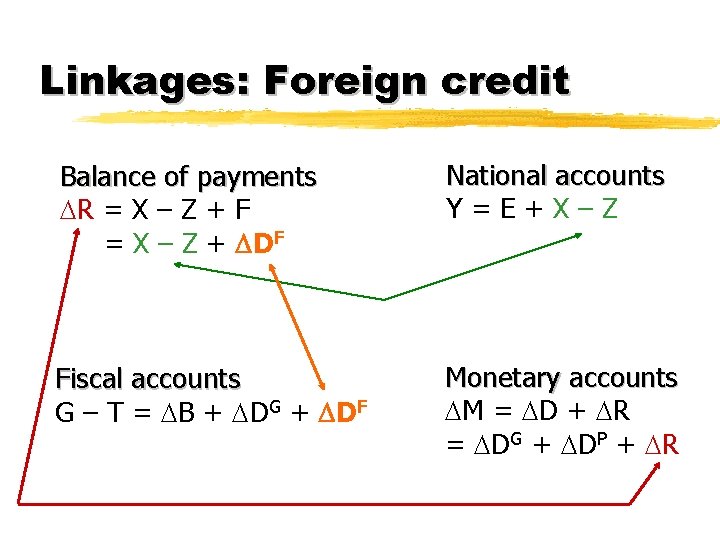
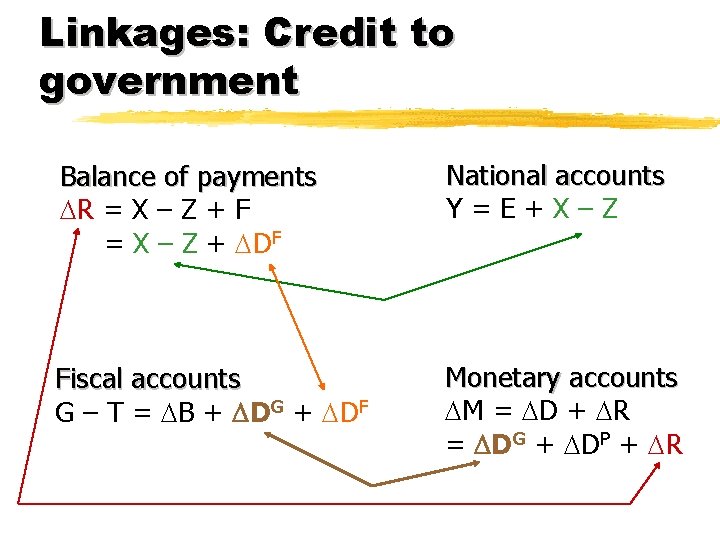
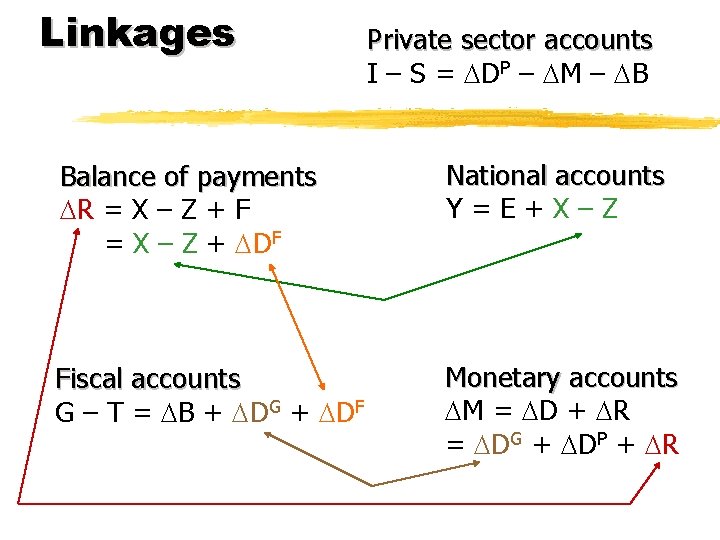
Linkages Balance of payments R = X – Z + F = X – Z + DF 2

Linkages Balance of payments R = X – Z + F = X – Z + DF National accounts Y=E+X–Z

Linkages Balance of payments R = X – Z + F = X – Z + DF Fiscal accounts G – T = B + DG + DF National accounts Y=E+X–Z

Linkages Balance of payments R = X – Z + F = X – Z + DF National accounts Y=E+X–Z Fiscal accounts G – T = B + DG + DF Monetary accounts M = D + R = DG + DP + R

Linkages: Reserves Balance of payments R = X – Z + F = X – Z + DF National accounts Y=E+X–Z Fiscal accounts G – T = B + DG + DF Monetary accounts M = D + R = DG + DP + R

Linkages: Current account Balance of payments R = X – Z + F = X – Z + DF National accounts Y=E+X–Z Fiscal accounts G – T = B + DG + DF Monetary accounts M = D + R = DG + DP + R

Linkages: Foreign credit Balance of payments R = X – Z + F = X – Z + DF National accounts Y=E+X–Z Fiscal accounts G – T = B + DG + DF Monetary accounts M = D + R = DG + DP + R

Linkages: Credit to government Balance of payments R = X – Z + F = X – Z + DF National accounts Y=E+X–Z Fiscal accounts G – T = B + DG + DF Monetary accounts M = D + R = DG + DP + R

Linkages Private sector accounts I – S = DP – M – B Balance of payments R = X – Z + F = X – Z + DF National accounts Y=E+X–Z Fiscal accounts G – T = B + DG + DF Monetary accounts M = D + R = DG + DP + R

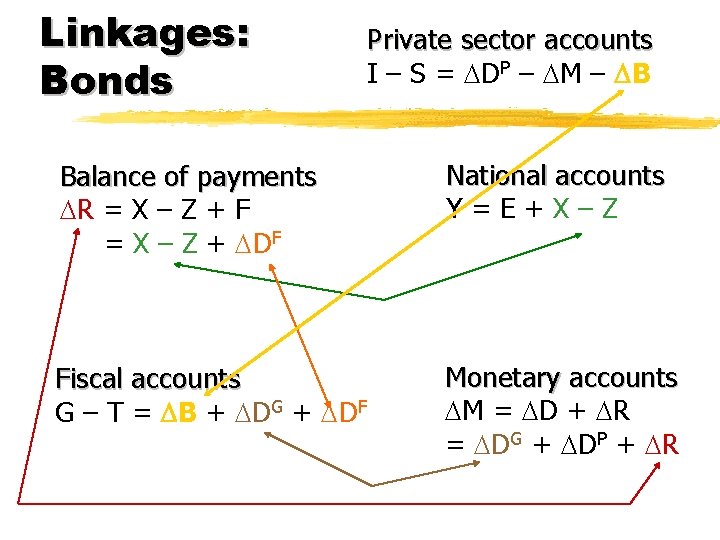
Linkages: Bonds Private sector accounts I – S = DP – M – B Balance of payments R = X – Z + F = X – Z + DF National accounts Y=E+X–Z Fiscal accounts G – T = B + DG + DF Monetary accounts M = D + R = DG + DP + R

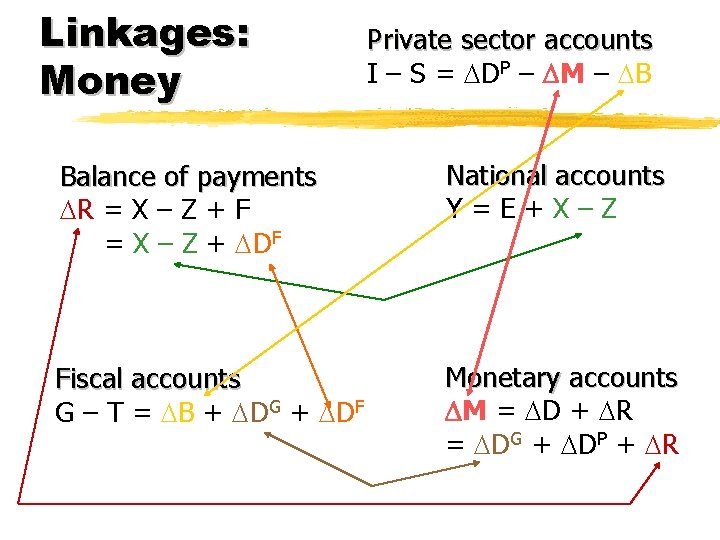
Linkages: Money Private sector accounts I – S = DP – M – B Balance of payments R = X – Z + F = X – Z + DF National accounts Y=E+X–Z Fiscal accounts G – T = B + DG + DF Monetary accounts M = D + R = DG + DP + R

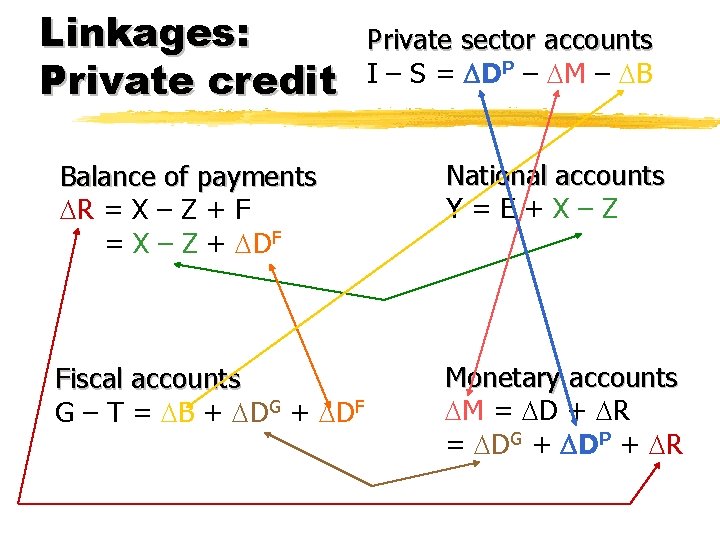
Linkages: Private credit Private sector accounts I – S = DP – M – B Balance of payments R = X – Z + F = X – Z + DF National accounts Y=E+X–Z Fiscal accounts G – T = B + DG + DF Monetary accounts M = D + R = DG + DP + R

Model 3 1. Express accounting linkages in terms of simple algebra 2. Use model to describe how nominal income and reserves depend on domestic credit 1. Demonstrate how BOP target translates into prescription for fiscal and monetary policy 2. Financial programming in action

List of variables M = money X = real exports D = domestic credit Px = price of exports R = foreign reserves Z = real imports R = R-R-1 = balance of Pz = price of imports payments F = capital inflow P = price level m = propensity to Y = real income import v = velocity Two behavioral v d n a m : s r te e m a r pa

List of relationships M=D+R M = (1/v)PY R = (1/v)PY – D R = Px. X – Pz. Z + F Pz. Z = m. PY R = Px. X – m. PY + F + R-1 (monetary survey) (money demand) (M schedule) (balance of payments) (import demand) (B schedule) Estimate m and v by regression analysis

The M schedule Reserves (R) M schedule R = (1/v)PY – D 1 v D up PY = v(R + D) An increase in reserves increases demand for money, and hence also income PY is nominal income GNP (PY)

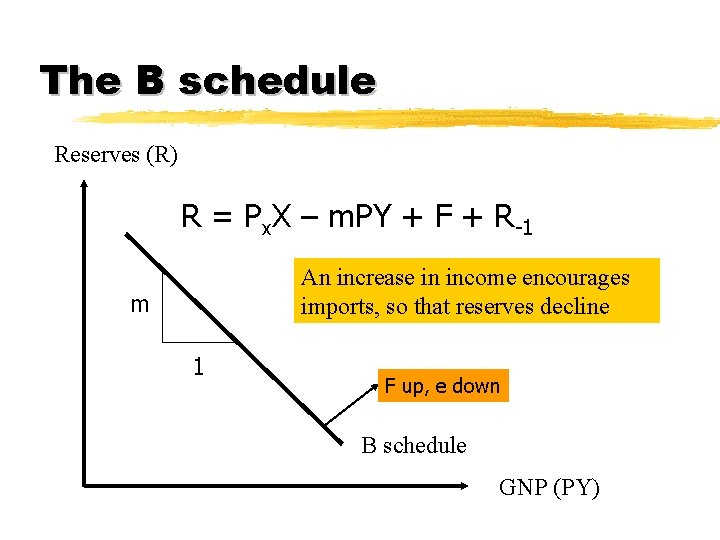
The B schedule Reserves (R) R = Px. X – m. PY + F + R-1 An increase in income encourages imports, so that reserves decline m 1 F up, e down B schedule GNP (PY)

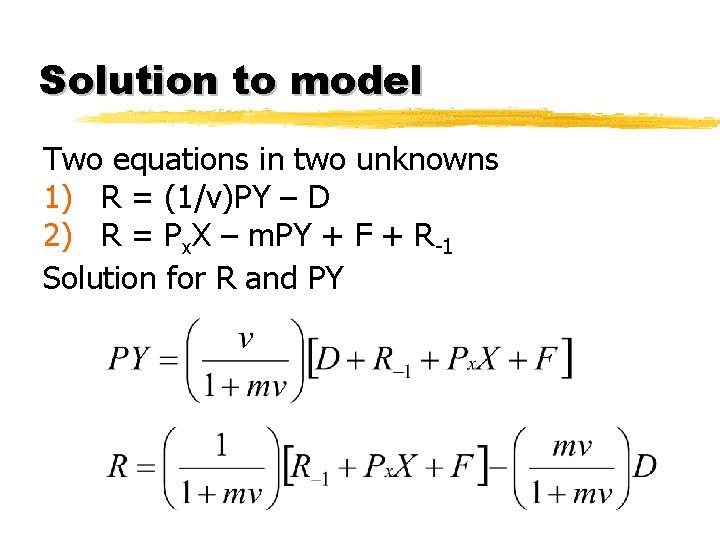
Solution to model Two equations in two unknowns 1) R = (1/v)PY – D 2) R = Px. X – m. PY + F + R-1 Solution for R and PY

Multipliers: Algebra

Multipliers: Numbers Suppose m = ¼ and v = 4 Credit multiplier Half of credit expansion leaks abroad through balance of payments

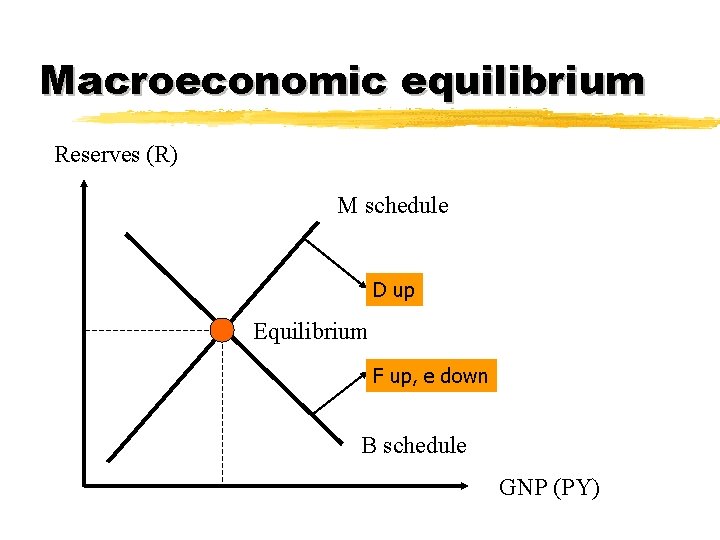
Macroeconomic equilibrium Reserves (R) M schedule D up Equilibrium F up, e down B schedule GNP (PY)

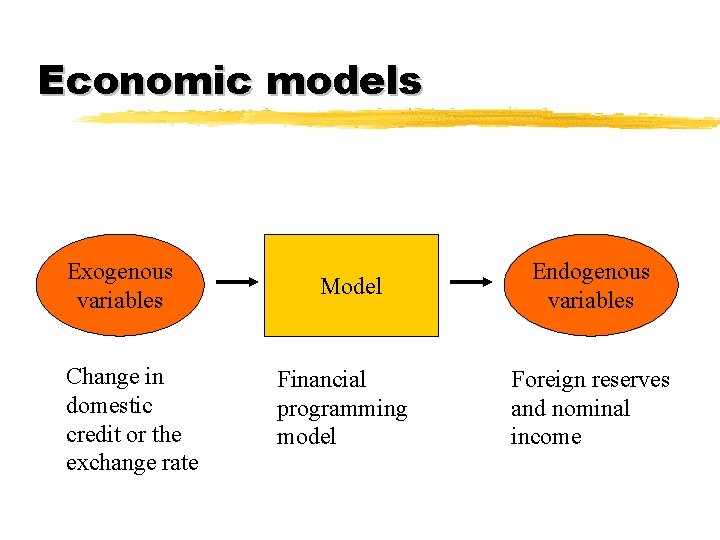
Economic models Exogenous variables Change in domestic credit or the exchange rate Model Financial programming model Endogenous variables Foreign reserves and nominal income

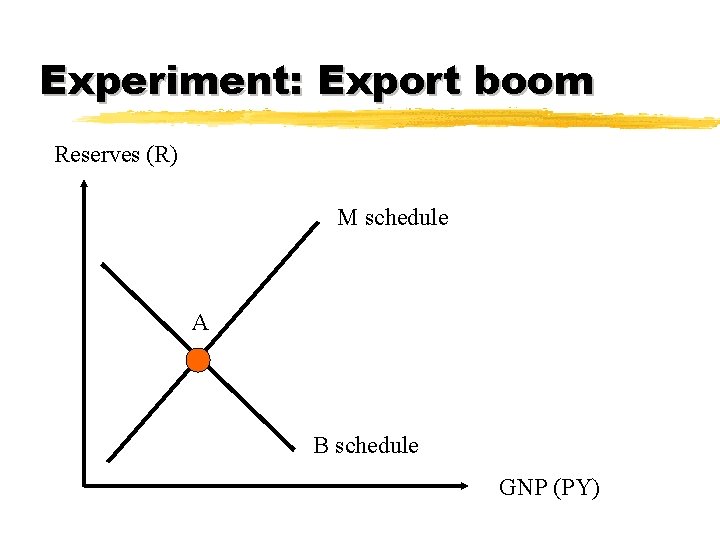
Experiment: Export boom Reserves (R) M schedule A B schedule GNP (PY)

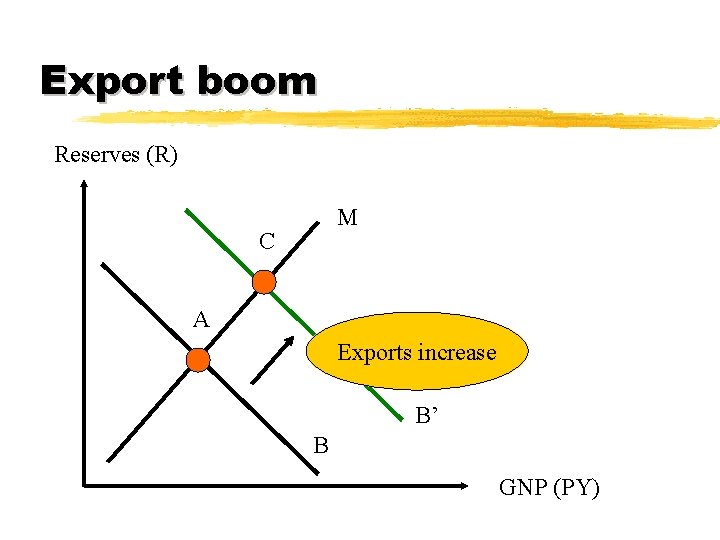
Export boom Reserves (R) M C A Exports increase B’ B GNP (PY)

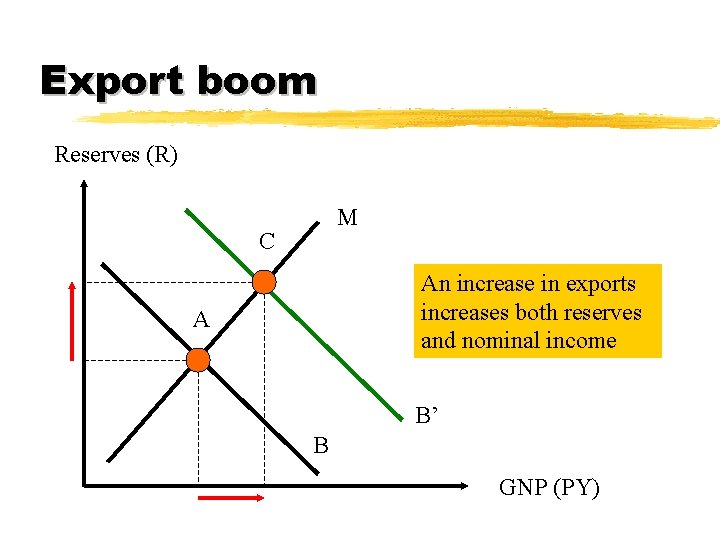
Export boom Reserves (R) M C An increase in exports increases both reserves and nominal income A B’ B GNP (PY)

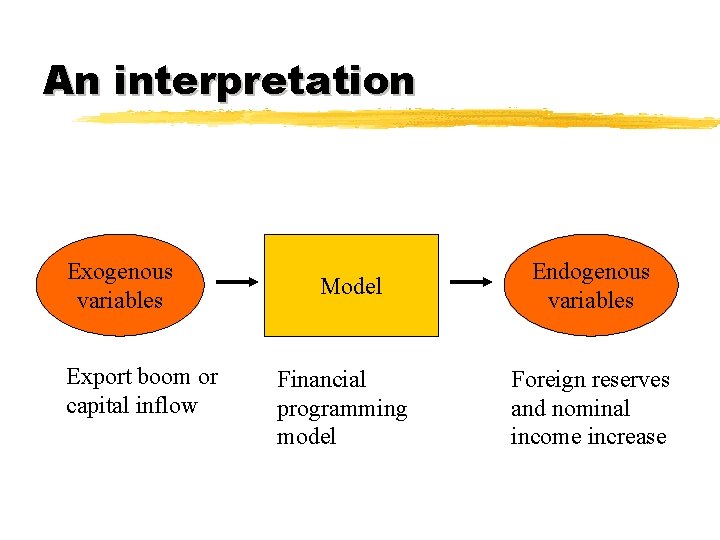
An interpretation Exogenous variables Export boom or capital inflow Model Financial programming model Endogenous variables Foreign reserves and nominal income increase

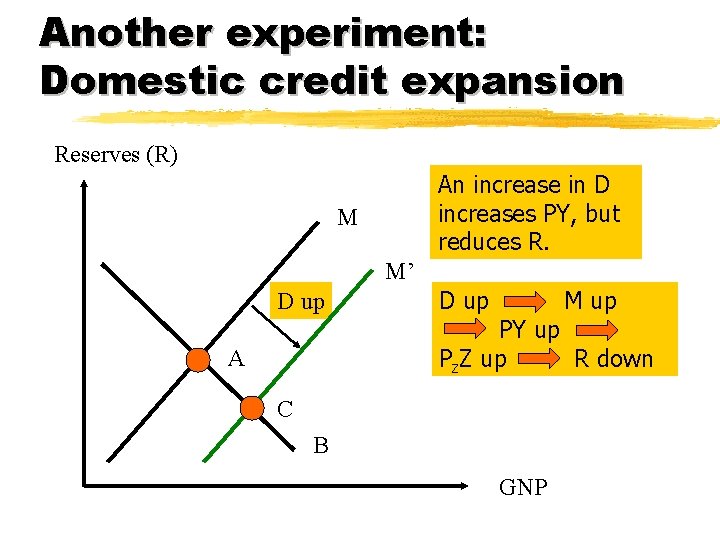
Another experiment: Domestic credit expansion Reserves (R) An increase in D increases PY, but reduces R. M M’ D up M up PY up Pz. Z up R down A C B GNP

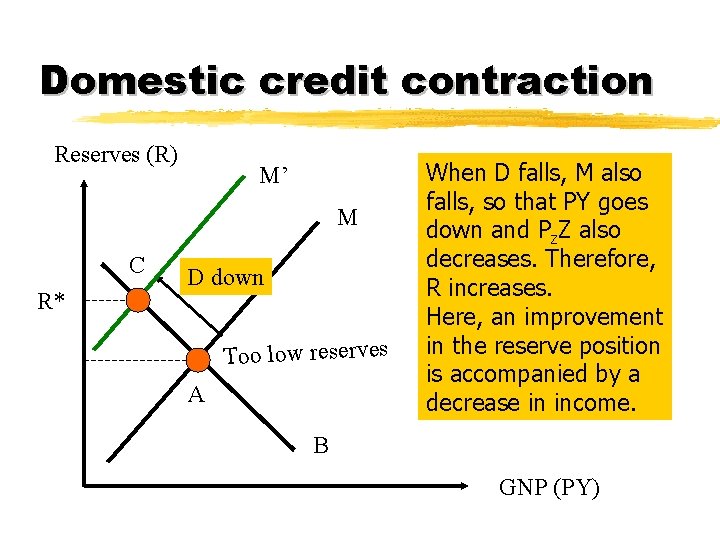
Domestic credit contraction Reserves (R) M’ M C R* D down Too low reserves A When D falls, M also falls, so that PY goes down and Pz. Z also decreases. Therefore, R increases. Here, an improvement in the reserve position is accompanied by a decrease in income. B GNP (PY)

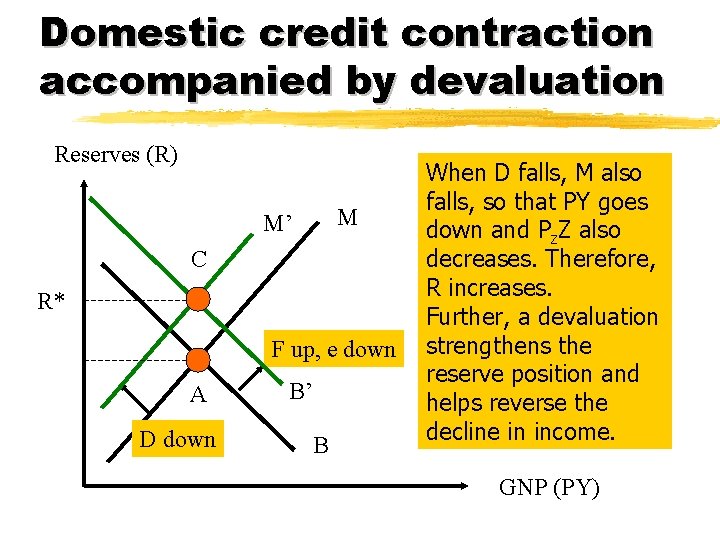
Domestic credit contraction accompanied by devaluation Reserves (R) M M’ C R* F up, e down A D down B’ B When D falls, M also falls, so that PY goes down and Pz. Z also decreases. Therefore, R increases. Further, a devaluation strengthens the reserve position and helps reverse the decline in income. GNP (PY)

Comparative statics: n io t la f in = P An overview D P x. X F e p R - + + - - PY + + + - +

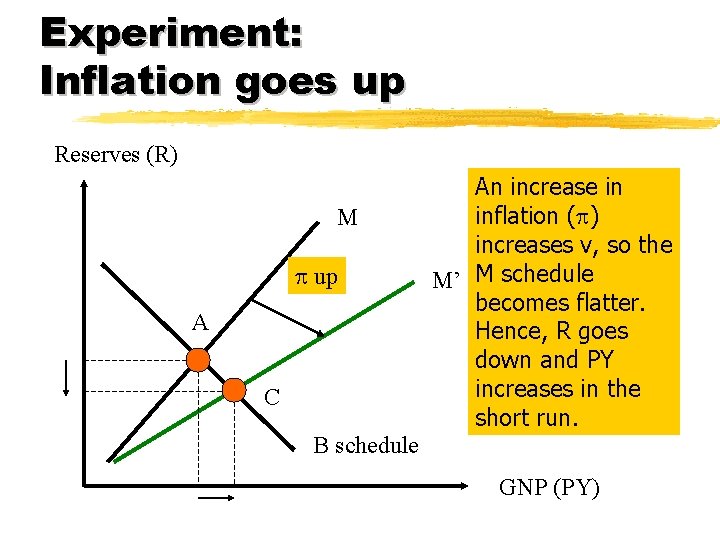
Experiment: Inflation goes up Reserves (R) M p up A C An increase in inflation (p) increases v, so the M’ M schedule becomes flatter. Hence, R goes down and PY increases in the short run. B schedule GNP (PY)

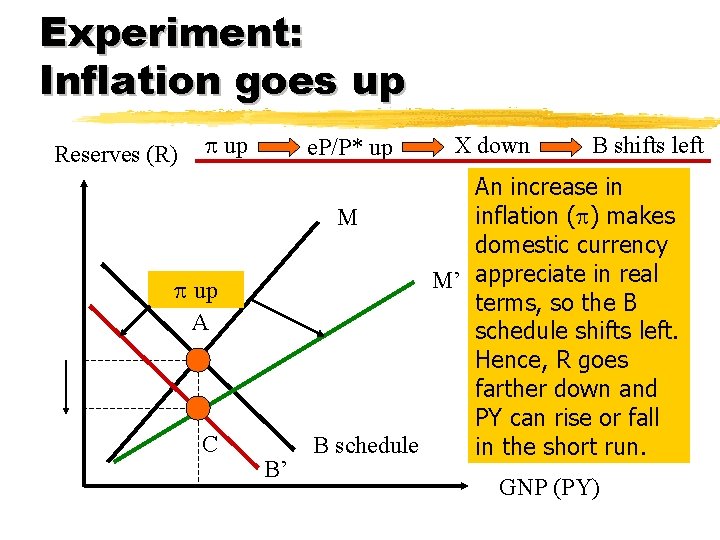
Experiment: Inflation goes up Reserves (R) p up e. P/P* up p up A C B’ X down B shifts left An increase in inflation (p) makes M domestic currency M’ appreciate in real terms, so the B schedule shifts left. Hence, R goes farther down and PY can rise or fall B schedule in the short run. GNP (PY)

Numerical example History and targets 4 q Record history, establish targets Forecasting q Make forecasts for balance of payments, output and inflation, money Policy decisions q Set domestic credit at a level that is consistent with forecasts as well as foreign reserve target

Financial programming step by step 1) Make forecasts, set reserve target R* – E. g. , reserves at 3 months of imports 2) Compute permissible imports from BOP – More imports will jeopardize reserve target 3) Infer permissible increase in nominal income from import equation 4) Infer monetary expansion consistent with increase in nominal income 5) Derive domestic credit as a residual: D = M – R*

History 1. 5 months = 6 weeks Known at beginning of program period: q M-1 = 800, D-1 = 700, R-1 = 100 Recall: M = D + R q Px. X-1 = 750, Z-1 = 800, F-1 = 50 Recall: R = Px. X – Pz. Z + F So, R-1 = 750 – 800 + 50 = 0 üCurrent account deficit, overall balance q R-1/Pz. Z-1 = 100/800 = 0. 125 üEquivalent to 1. 5 (= 0. 125 • 12) months of imports üWeak reserve position

Forecast for balance of payments Px. X grows by a third, so Px. X = 1, 000 F doubles, so F = 100 Suppose R* is set at 240. Then BOP forecasts Pz. Z = Px. X + F + R-1 – R* = 1, 000 + 100 – 240 = 960 Level of imports is consistent with R* R*/Pz. Z = 240/960 = 0. 25 üEquivalent to 3 (= 0. 25 • 12) months of imports

Forecast for real sector Increase in Pz. Z from 800 to 960, i. e. , by 20%, is consistent with R* equivalent to 3 months of imports Now, recall that Pz. Z depends on PY where P is price level and Y is output Hence, if income elasticity of import demand is 1, PY can increase by 20% üE. g. , 5% growth and 15% inflation

Forecast for money Recall M = D + R If PY can increase by 20%, then, if income elasticity of money demand is 1, M can also increase by 20% Recall quantity theory of money MV = PY Constant velocity means that % M = % PY = ˜ % P + % Y Hence, M can expand from 800 to 960

Determination of credit Having set reserve target at R* = 240 and forecast M at 960, we can now compute level of credit that is consistent with our reserve target, based on M = D + R So, D = 960 – 240 = 720, up from 700 D/D-1 = 20/700 = 2. 9% üQuite restrictive, given that PY rises by 20% üImplies substantial reduction in domestic credit in real terms

Forecast for balance of So try again payments Px. X grows by a third, so Px. X = 1, 000 F doubles, so F = 100, as before R* is now set at 200, not 240. Then BOP forecasts Pz. Z = Px. X + F + R-1 – R* = 1, 000 + 100 – 200 = 1, 000 Level of imports is consistent with R* R*/Pz. Z = 200/1000 = 0. 2 üEquivalent to 2. 4 (= 0. 2 • 12) months of imports

Forecast for real sector Increase in Pz. Z from 800 to 1, 000, i. e. , by 25%, is consistent with R* equivalent to 2. 4 months of imports Now, recall that Pz. Z depends on PY where P is price level and Y is output Hence, if income elasticity of import demand is 1, PY can increase by 25% üE. g. , 5% growth and 20% inflation, roughly

Forecast for money Recall M = D + R If PY can increase by 25%, then, if income elasticity of money demand is 1, M can also increase by 25% However, if income elasticity of money demand is 0. 8, M can increase by only 20% as before Hence, if the income elasticity is 1, M can expand from 800 to 1, 000

Determination of credit Having set reserve target at R* = 200 and forecast M at 1, 000, we can now compute level of credit that is consistent with our reserve target, based on M = D + R So, D = 1, 000 – 200 = 800, up from 700 D/D-1 = 100/700 = 14% üStill restrictive, given that PY rises by 25%, but less restrictive than before

History Once more Known at beginning of program period: q M-1 = 800, D-1 = 700, R-1 = 100 Recall: M = D + R q X-1 = 500, Z-1 = 600, F-1 = 50 Recall: R = Px. X – Pz. Z + F So, R-1 = 500 – 600 + 50 = -50 üCurrent account deficit (-100), smaller overall deficit q R-1/Pz. Z-1 = 100/600 = 0. 167 üEquivalent to 2 (= 0. 167*12) months of imports üWeak reserve position

Forecast for balance of payments Px. X grows by 40%, so Px. X = 700 F doubles, so F = 100 Suppose R* is set at 180. Then BOP forecasts Pz. Z = Px. X + F + R-1 – R* = 700 + 100 – 180 = 720 Level of imports is consistent with R* R*/Pz. Z = 180/720 = 0. 25 üEquivalent to 3 (= 0. 25*12) months of imports

Forecast for real sector Increase in Pz. Z from 600 to 720, i. e. , by 20%, is consistent with R* equivalent to 3 months of imports But Pz. Z depends on PY where P is price level and Y is output Hence, if income elasticity of import demand is 1, PY can increase by 20% üE. g. , 5% growth and 15% inflation

Forecast for money Recall M = D + R If PY can increase by 20%, then, if income elasticity of money demand is 1, M can also increase by 20% Hence, M can expand from 800 to 960

Determination of credit Having set reserve target at R* = 180 and forecast M at 960, we can now compute level of credit that is consistent with our reserve target So, D = 960 – 180 = 780, up from 700 D/D-1 = 80/700 = 11% üQuite restrictive, given that PY rises by 25% üImplies substantial reduction in domestic credit in real terms

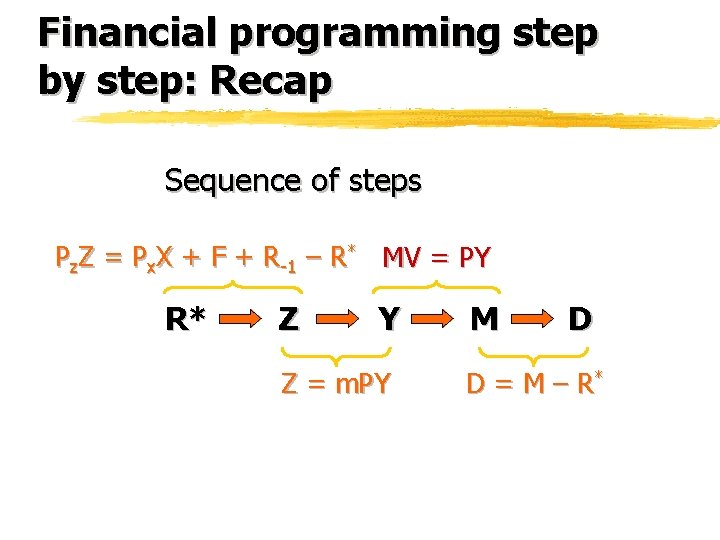
Financial programming step by step: Recap Sequence of steps Pz. Z = Px. X + F + R-1 – R* MV = PY R* Z Y Z = m. PY M D D = M – R*

Conclusion These slides will be posted on my website: www. hi. is/~gylfason q Financial programming is an oral tradition that spans the entire history of the IMF q When expressed in simple algebra, financial programming is not to be taken literally as a one-size-fits-all model d n E e h T üFund economists understand that countries differ, and they seek to help tailor financial programs to the needs of individual countries üEven so, certain fundamental principles and relationships apply everywhere