FIGHTING ADVERSARIES IN NETWORKS Sidharth Jaggi MIT Michelle

FIGHTING ADVERSARIES IN NETWORKS Sidharth Jaggi (MIT) Michelle Effros Michael Langberg Tracey Ho Philip Chou Kamal Jain Muriel Médard Dina Katabi Peter Sanders Ludo Tolhuizen Sebastian Egner

Network Coding. . . what is it? “The core notion of network coding is to allow and encourage mixing of data at intermediate network nodes. “ (Network Coding Homepage)

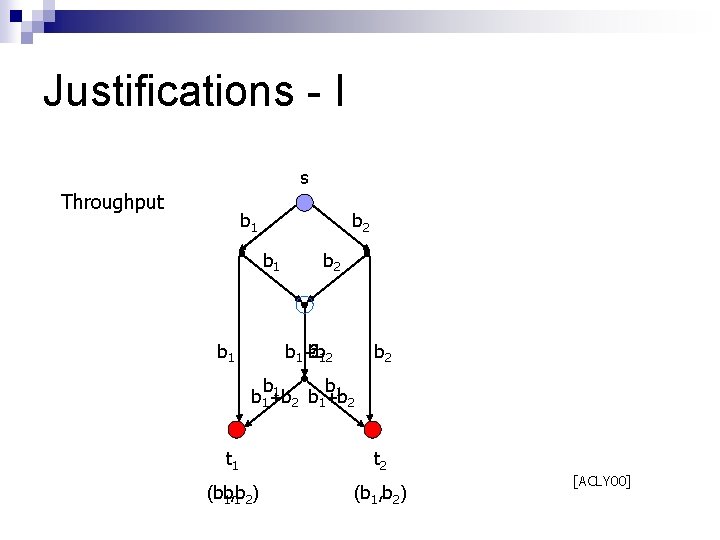
Justifications - I s Throughput b 1 b 2 ? b 1+b b 1 2 b 1 b 1+b b +b 2 1 2 t 1 t 2 (b 1 b, b 1 2) (b 1, b 2) [ACLY 00]

Gap Without Coding s [JSCEEJT 05]. . . Coding capacity = h Routing capacity≤ 2

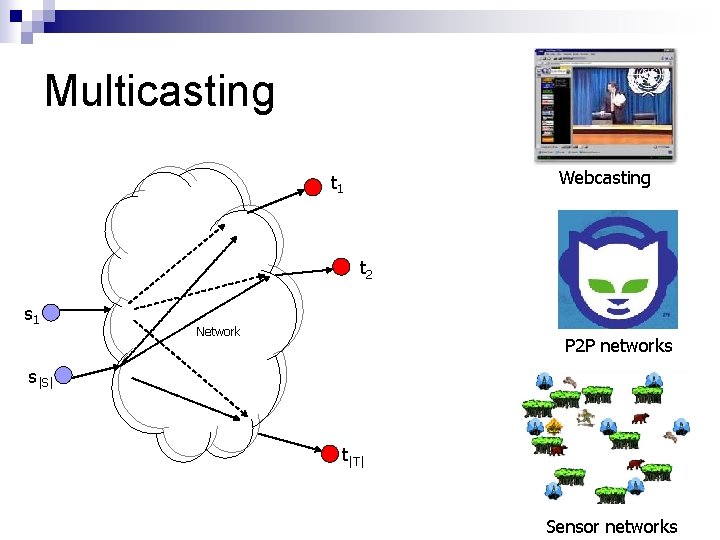
Multicasting Webcasting t 1 t 2 s 1 Network P 2 P networks s|S| t|T| Sensor networks

Background Upper bound for multicast capacity C, C ≤ min{Ci} t 1 [ACLY 00] - achievable! C 1 C 2 t 2 s Network C|T| t|T| [LYC 02] - linear codes suffice!! [KM 01] - “finite field” linear codes suffice!!!

Background F(2 m)-linear network b 1 b 2 bm [KM 01] Source: - Group together `m’ bits, Every node: - Perform linear combinations β 1 β 2 βk over finite field F(2 m)

Background t 1 [ACLY 00] - achievable! C 1 C 2 t 2 s Network [LYC 02] - linear codes suffice!! [KM 01] - “finite field” linear codes suffice!!! [JCJ 03], [SET 03] - polynomial time code design!!!! C|T| t|T| [HKMKE 03], [JCJ 03] - random distributed code design!!!!!

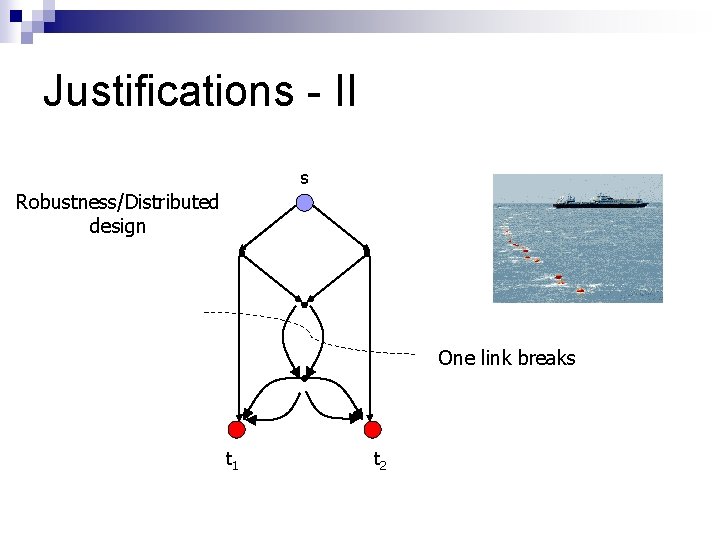
Justifications - II s Robustness/Distributed design One link breaks t 1 t 2

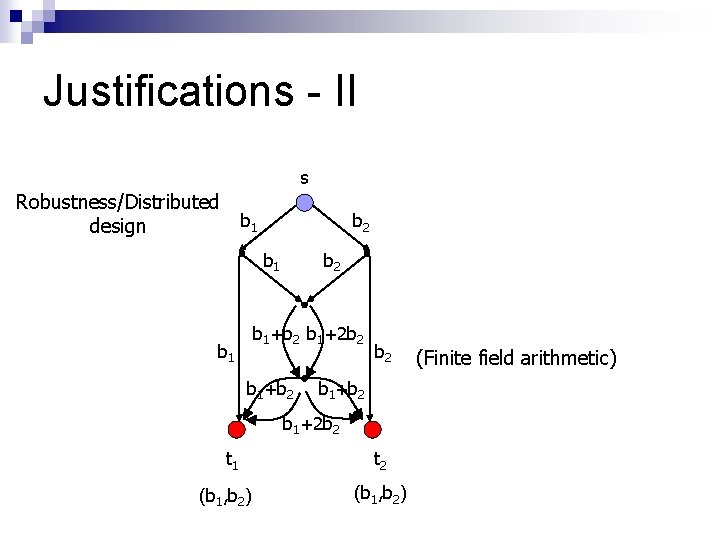
Justifications - II s Robustness/Distributed design b 1 b 2 b 1+b 2 b 1+2 b 2 b 1+b 2 b 1+2 b 2 t 1 (b 1, b 2) t 2 (b 1, b 2) (Finite field arithmetic)

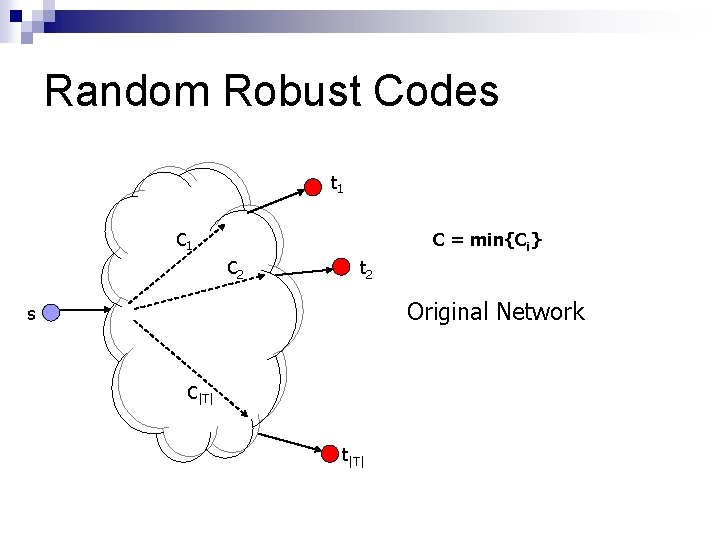
Random Robust Codes t 1 C = min{Ci} C 2 t 2 Original Network s C|T| t|T|

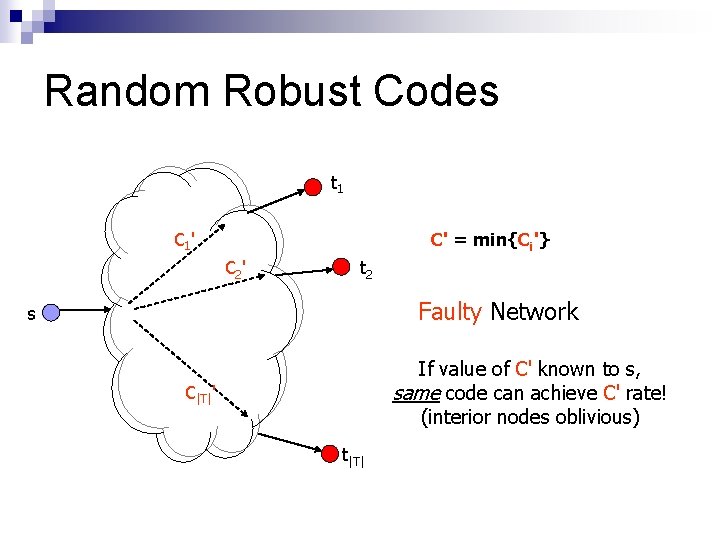
Random Robust Codes t 1 C 1 ' C' = min{Ci'} C 2 ' t 2 Faulty Network s If value of C' known to s, same code can achieve C' rate! (interior nodes oblivious) C|T|' t|T|

Random Robust Codes Choose random [ß] at each node Percolate overall transfer function down network With high probability, invertible Decentralized design

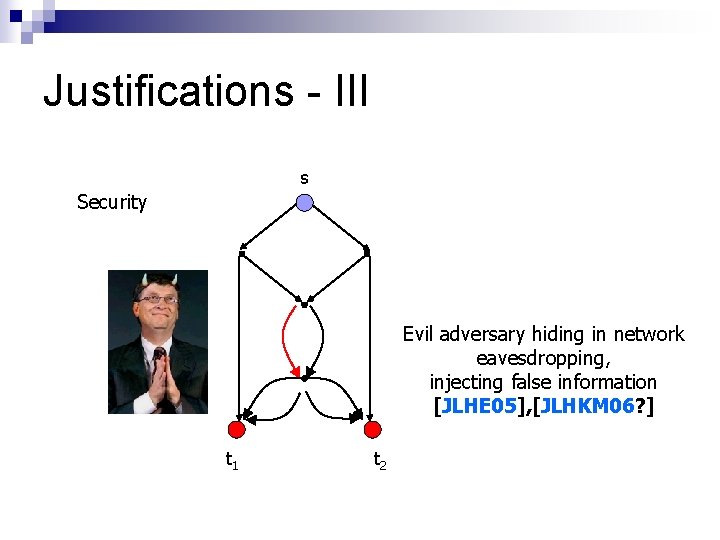
Justifications - III s Security Evil adversary hiding in network eavesdropping, injecting false information [JLHE 05], [JLHKM 06? ] t 1 t 2

Aha! Network Coding!!! Greater throughput Robust against random errors. . .

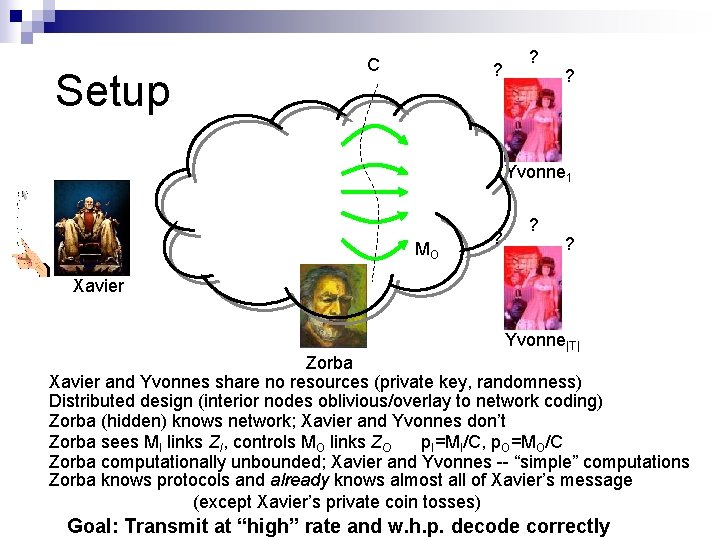
? ? ? Yvonne 1. . . ? Xavier ? ? Yvonne|T| Zorba

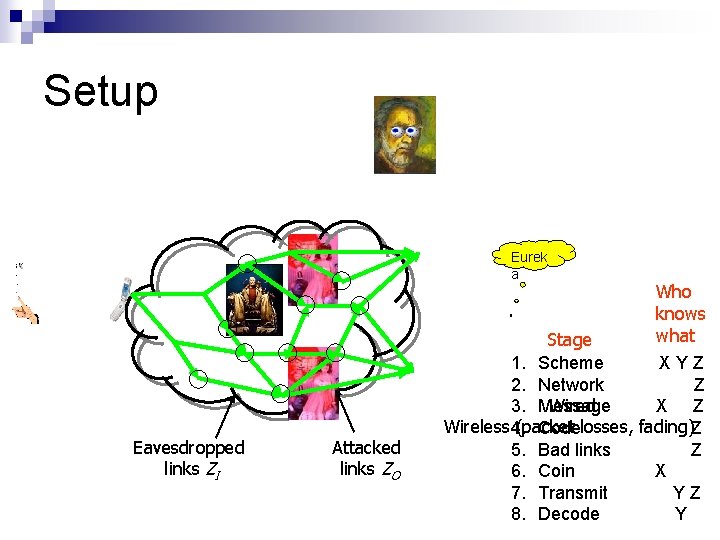
Setup Eurek a Eavesdropped links ZI Attacked links ZO Who knows what Stage 1. Scheme XYZ 2. Network Z Wired 3. Message X Z Wireless 4. (packet Codelosses, fading)Z 5. Bad links Z 6. Coin X 7. Transmit YZ 8. Decode Y

Setup C ? ? ? Yvonne 1 MO ? ? ? Xavier Yvonne|T| Zorba Xavier and Yvonnes share no resources (private key, randomness) Distributed design (interior nodes oblivious/overlay to network coding) Zorba (hidden) knows network; Xavier and Yvonnes don’t Zorba sees MI links ZI, controls MO links ZO p. I=MI/C, p. O=MO/C Zorba computationally unbounded; Xavier and Yvonnes -- “simple” computations Zorba knows protocols and already knows almost all of Xavier’s message (except Xavier’s private coin tosses) Goal: Transmit at “high” rate and w. h. p. decode correctly

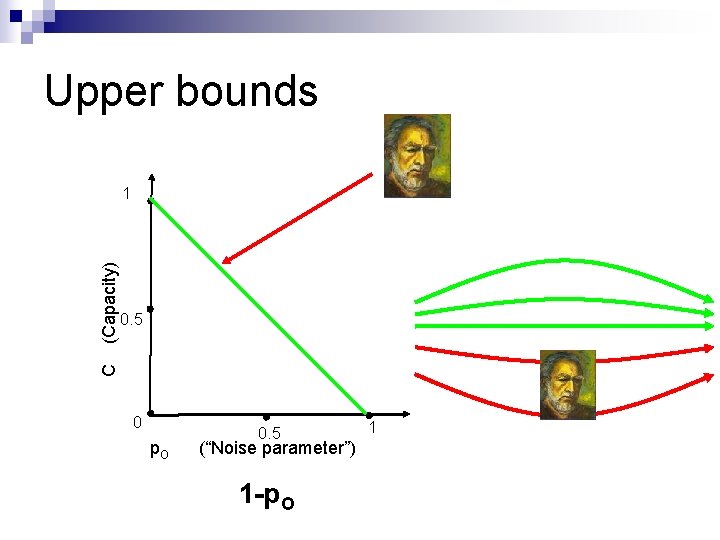
Upper bounds 0. 5 C (Capacity) 1 0 p. O 0. 5 (“Noise parameter”) 1 -p. O 1

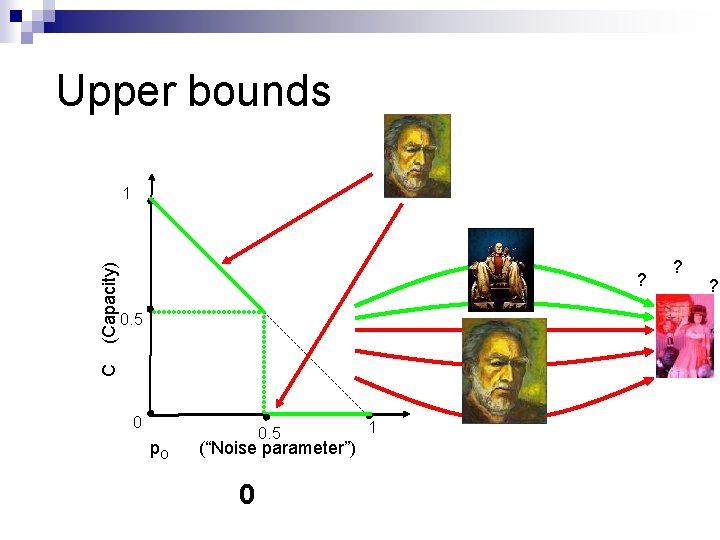
Upper bounds ? 0. 5 C (Capacity) 1 0 p. O 0. 5 (“Noise parameter”) 0 1 ? ?

Unicast [JLHE 05] 0. 5 C (Capacity) 1 0 p. I=p. O 0. 5 1 (“Noise parameter” = “Knowledge parameter”)

Unicast [Folklore] C (Capacity) 1 0 p. O 0. 5 1 (“Noise parameter”) (“Knowledge parameter” p. I=1)

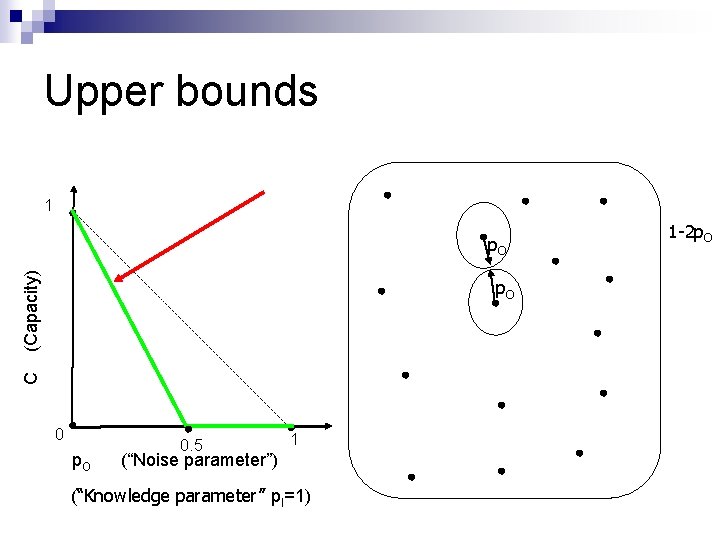
Upper bounds 1 (Capacity) p. O C p. O 0. 5 1 (“Noise parameter”) (“Knowledge parameter” p. I=1) 1 -2 p. O

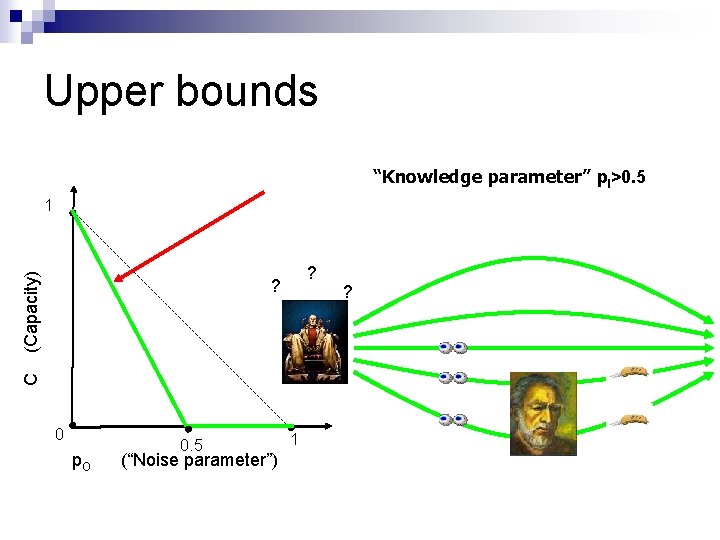
Upper bounds “Knowledge parameter” p. I>0. 5 (Capacity) 1 ? C ? 0 p. O 0. 5 (“Noise parameter”) 1 ?

Upper bounds “Knowledge parameter” p. I<0. 5 “Knowledge parameter” p. I>0. 5 (Capacity) 1 C 0. 5 C (Capacity) 1 0 p. O 0. 5 (“Noise parameter”) 1

Distributed Design [HKMKE 03] Choose random [ß] at each node Percolate overall transfer function down network With high probability, invertible Decentralized design

Distributed Design [HKMKE 03] Rate h=C xb(i) Block t 1 y 1 xs(j) hxh identity h<<n matrix S Slice xb(1) xb(i) xb(h) x β 1 βi βh x’b(i) T ys(j)=Txs(j)=T-1 ys(j) t|T| y|T|

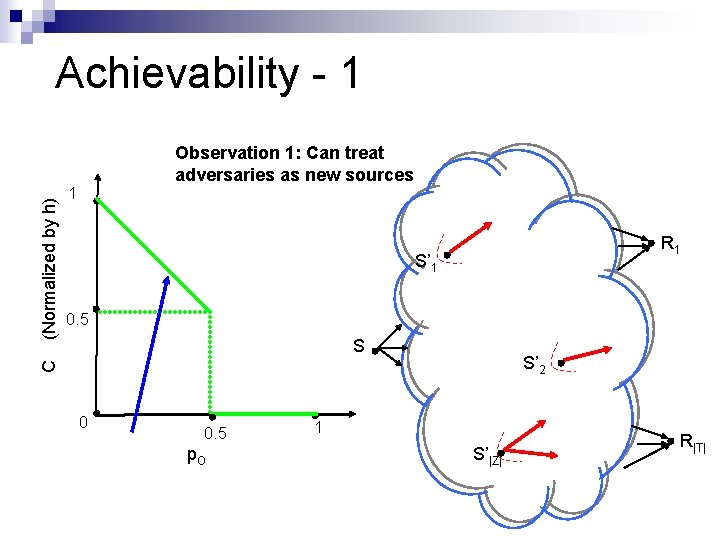
Achievability - 1 1 R 1 S’ 1 0. 5 S S’ 2 C (Normalized by h) Observation 1: Can treat adversaries as new sources 0 0. 5 p. O 1 S’|Z| R|T|

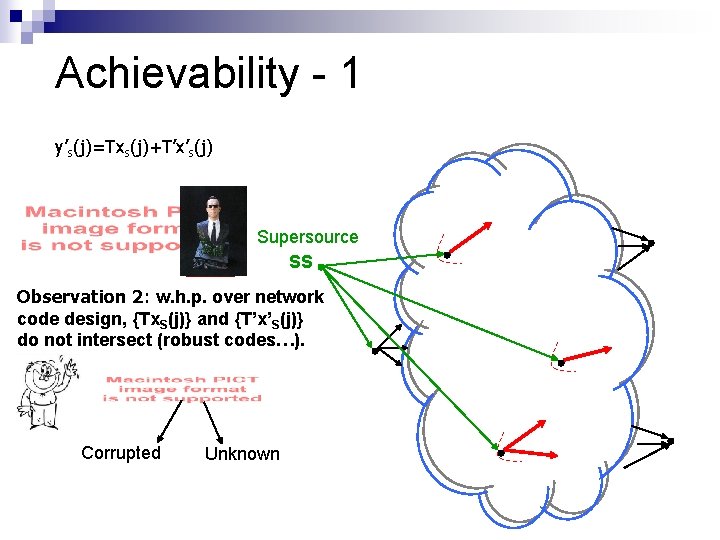
Achievability - 1 y’s(j)=Txs(j)+T’x’s(j) Supersource SS Observation 2: w. h. p. over network code design, {Tx. S(j)} and {T’x’S(j)} do not intersect (robust codes…). Corrupted Unknown

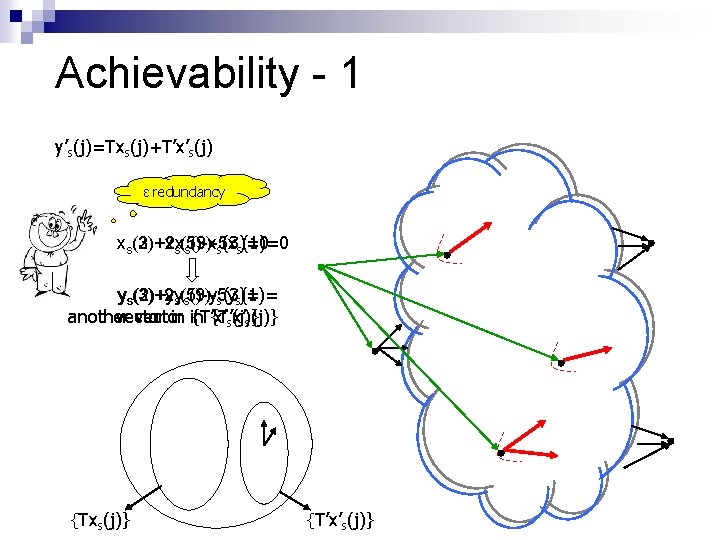
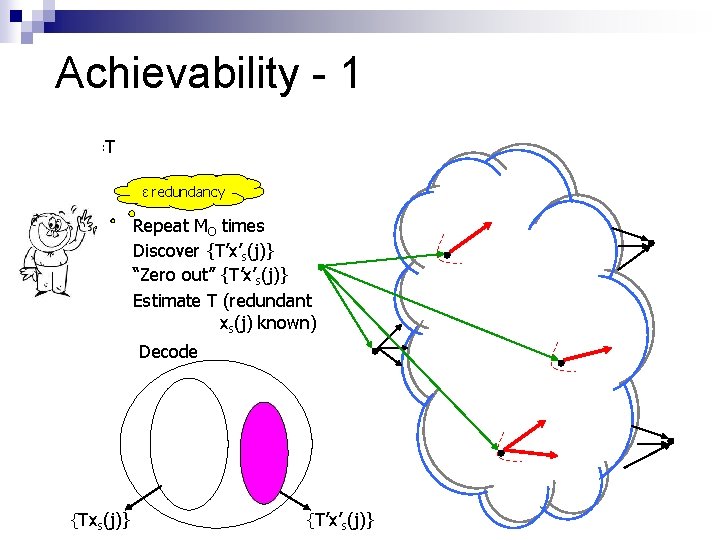
Achievability - 1 y’s(j)=Txs(j)+T’x’s(j) ε redundancy xs(3)+2 x (2)+xs(5)-x s(9)-5 x s(3)=0 s(1)=0 ys(3)+2 y (2)+ys(5)-y s(9)-5 y s(3)= s(1)= another vector in in {T’x’ s(j)} {Txs(j)} {T’x’s(j)}

Achievability - 1 y’s(j)=Txs(j)+T’x’s(j) ε redundancy Repeat MO times Discover {T’x’s(j)} “Zero out” {T’x’s(j)} Estimate T (redundant xs(j) known) Decode {Txs(j)} {T’x’s(j)}

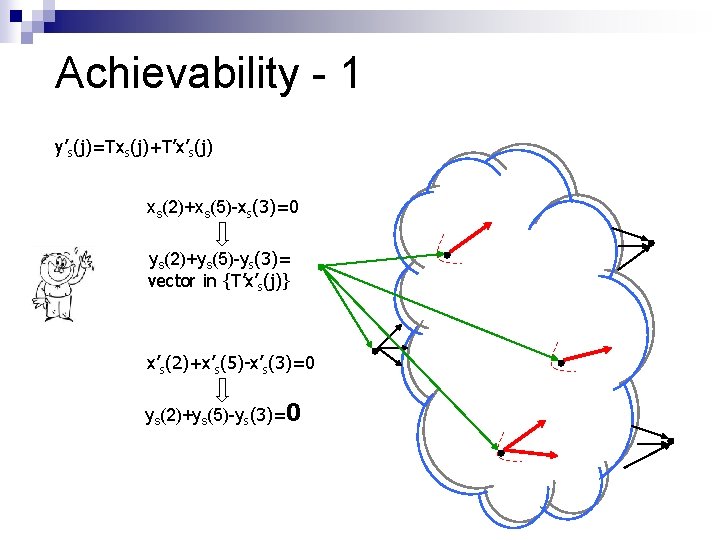
Achievability - 1 y’s(j)=Txs(j)+T’x’s(j) xs(2)+xs(5)-xs(3)=0 ys(2)+ys(5)-ys(3)= vector in {T’x’s(j)} x’s(2)+x’s(5)-x’s(3)=0 ys(2)+ys(5)-ys(3)=0

Secret Uncorrupted ε-rate Channels Secret, correct hashes of xs(j) [r, (∑jxs(j)rj)] Zorba doesn’t know how to hide Useful abstraction Will return to this…

Achievability - 2 “Distributed Network Error-correcting Code” (Knowledge parameter p. I>0. 5) [CY 06] – bounds, high complexity construction [JHLMK 06? ] – tight, poly-time construction C (Capacity) 1 0 p. O 0. 5 (“Noise parameter”) 1

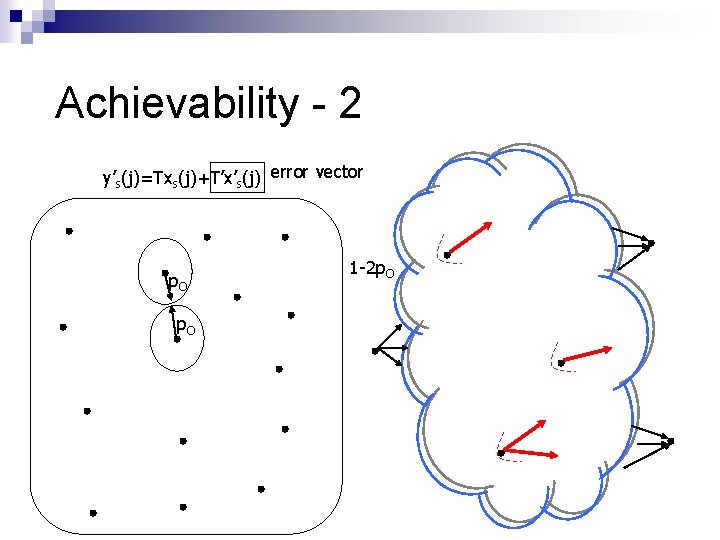
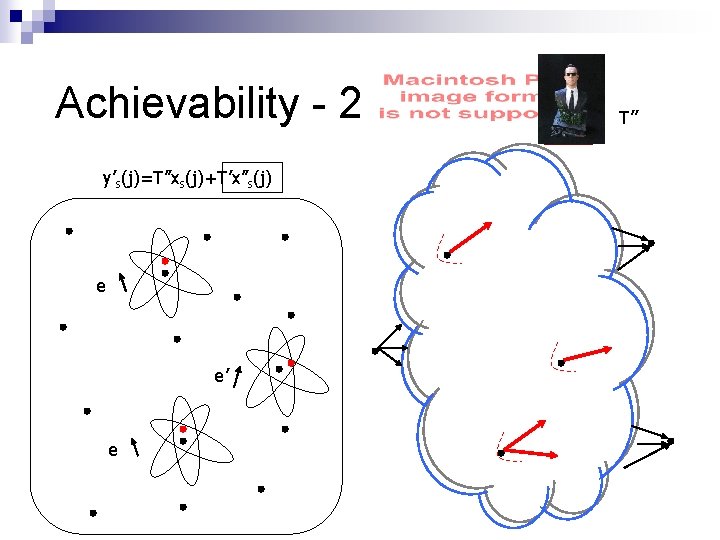
Achievability - 2 y’s(j)=Txs(j)+T’x’s(j) error vector p. O 1 -2 p. O

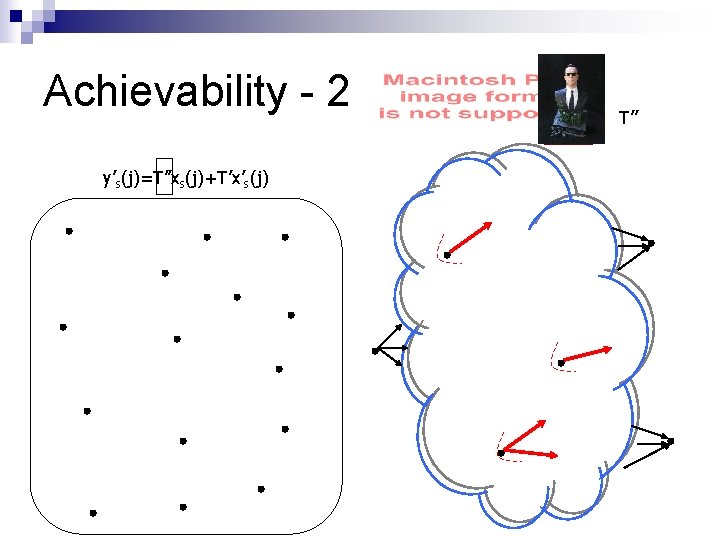
Achievability - 2 y’s(j)=T’’xs(j)+T’x’s(j) T’’

Achievability - 2 y’s(j)=T’’xs(j)+T’x’’s(j) e e’ e T’’

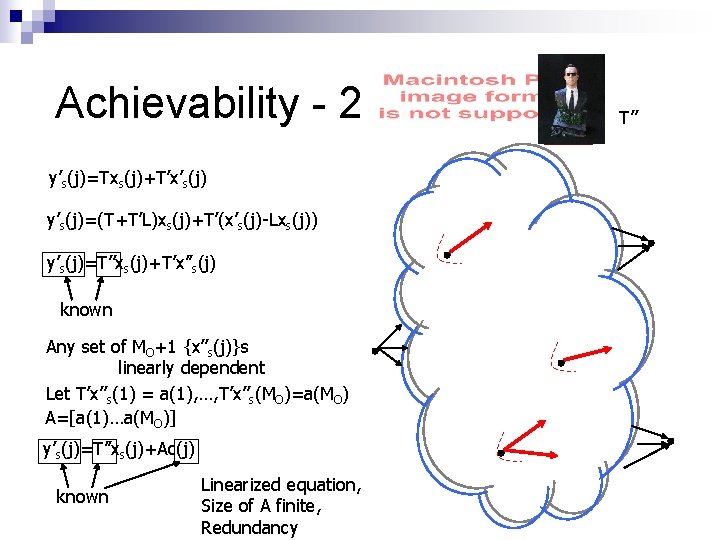
Achievability - 2 y’s(j)=Txs(j)+T’x’s(j) y’s(j)=(T+T’L)xs(j)+T’(x’s(j)-Lxs(j)) y’s(j)=T’’xs(j)+T’x’’s(j) known Any set of MO+1 {x’’s(j)}s linearly dependent Let T’x’’s(1) = a(1), …, T’x’’s(MO)=a(MO) A=[a(1)…a(MO)] y’s(j)=T’’xs(j)+Ac(j) known Linearized equation, Size of A finite, Redundancy T’’

Achievability - 1. 5 Not quite 2 MO<C, 2 MI<C MI+2 MO<C MI<C-2 MO Zorba’s observations Network error-correcting codes Using network error-correcting codes as small header, can transmit secret, correct information… … which can be used for first scheme!

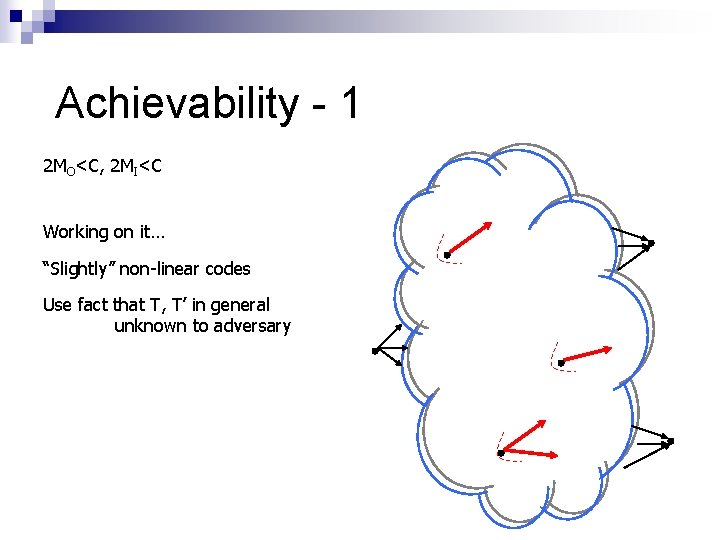
Achievability - 1 2 MO<C, 2 MI<C Working on it… “Slightly” non-linear codes Use fact that T, T’ in general unknown to adversary

Overview Hidden, eavesdropping, malicious, computationally unbounded adversary n Network topology unknown n Polynomial time decoding overlaid on network code, achieves “almost optimal” performance n

T H E E N D