Hongyi Yao Tsinghua University Sidharth Jaggi Chinese University

Hongyi Yao Tsinghua University Sidharth Jaggi Chinese University of Hong Kong Theodoros Dikaliotis California Institute of Technology Tracey Ho California Institute of Technology

MANIACs

MANIACs Multiple Access Network Informationflow And Correction codes

MANIACs Multiple Access Network Informationflow And Correction codes

MANIACs Multiple Access Network Informationflow And Correction codes

MANIACs Multiple Access Network Informationflow And Correction codes

MANIACs Multiple Access Network Informationflow And Correction codes

MANIACs Multiple Access Network Informationflow And Correction codes

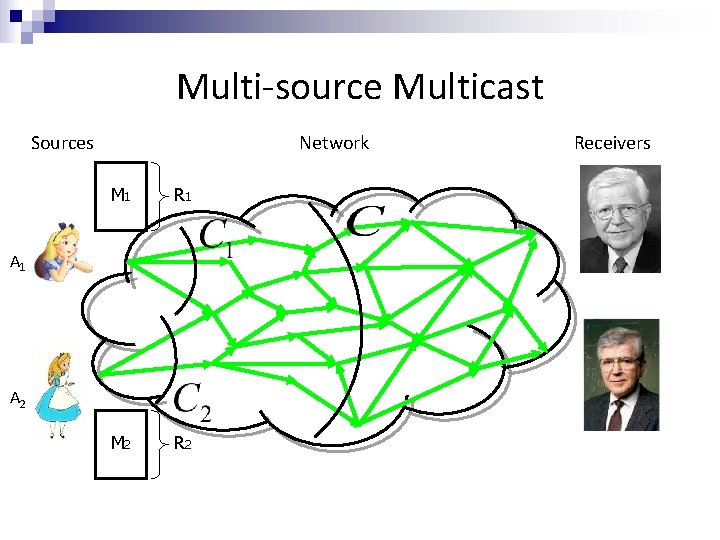
Multi-source Multicast Sources Network M 1 R 1 M 2 R 2 A 1 A 2 Receivers

Multi-source Multicast Sources Network M 1 R 1 M 2 R 2 A 1 A 2 Receivers

Multi-source Multicast Sources Network M 1 R 2 C 2 A 1 Receivers R 1+R 2=C A 2 M 2 R 2 C 1 R 1

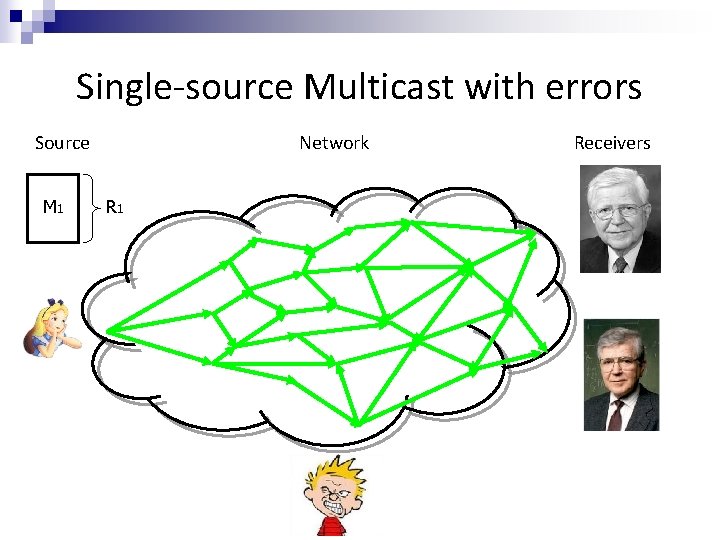
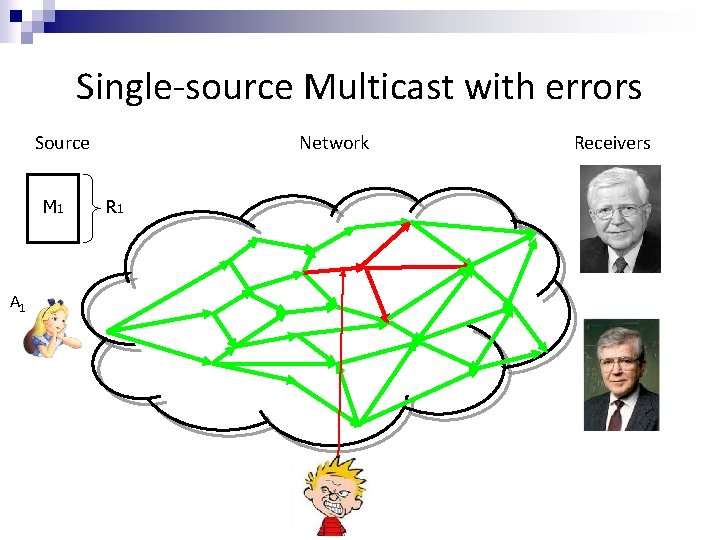
Single-source Multicast with errors Source M 1 Network R 1 Receivers

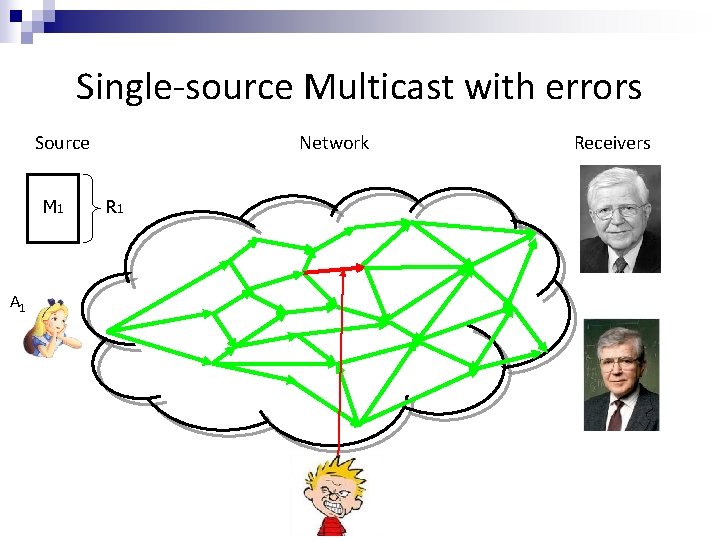
Single-source Multicast with errors Source M 1 A 1 Network R 1 Receivers

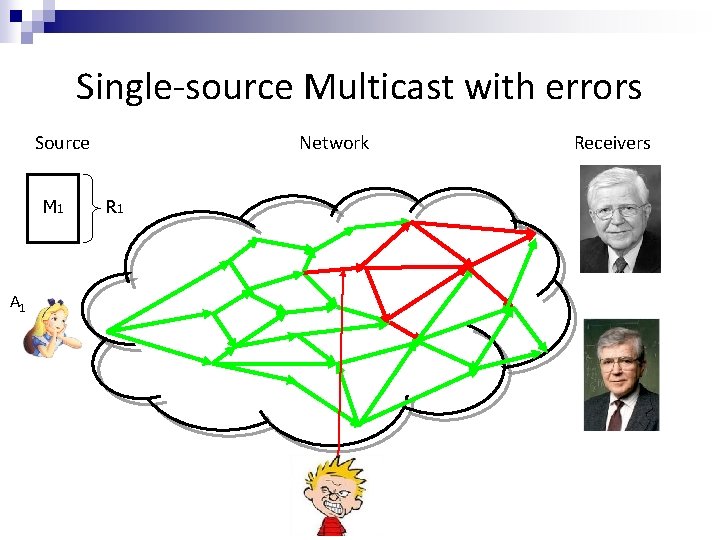
Single-source Multicast with errors Source M 1 A 1 Network R 1 Receivers

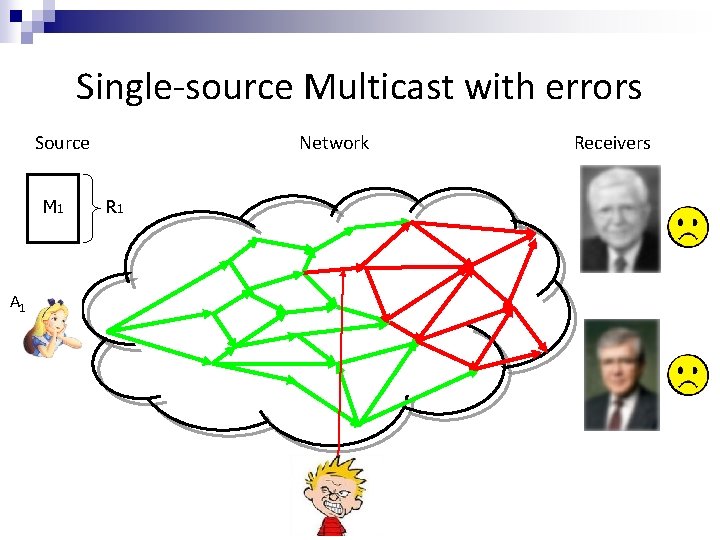
Single-source Multicast with errors Source M 1 A 1 Network R 1 Receivers

Single-source Multicast with errors Source M 1 A 1 Network R 1 Receivers

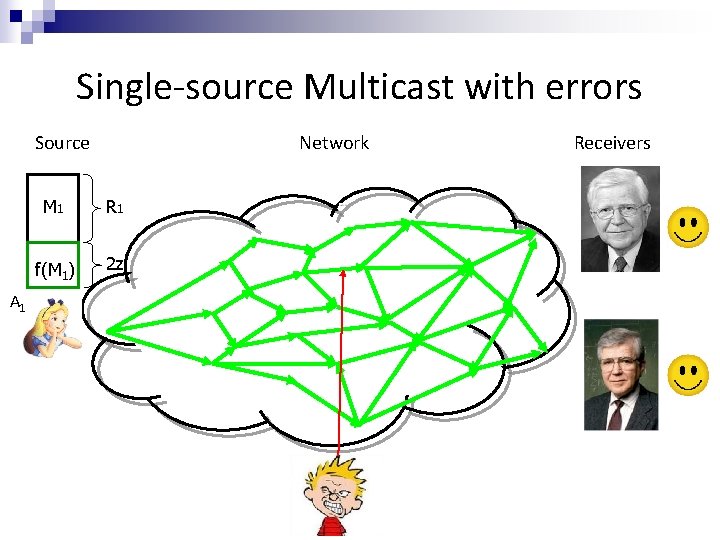
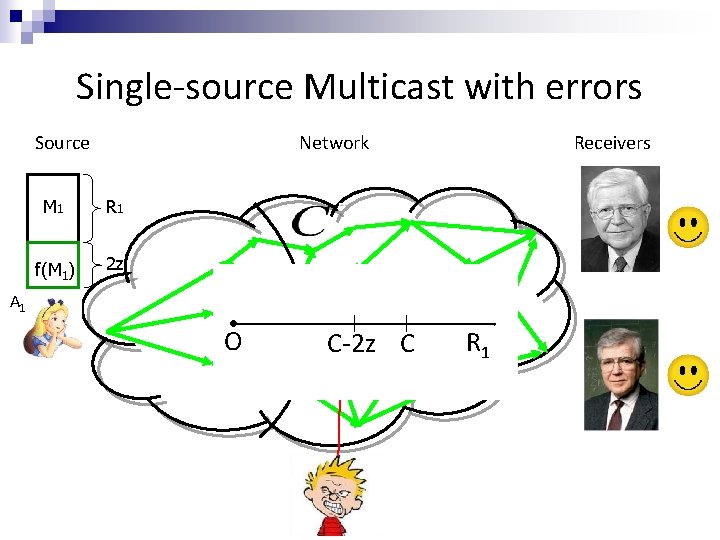
Single-source Multicast with errors Source A 1 Network M 1 R 1 f(M 1) 2 z Receivers

Single-source Multicast with errors Source Network M 1 R 1 f(M 1) 2 z Receivers A 1 O C-2 z C R 1

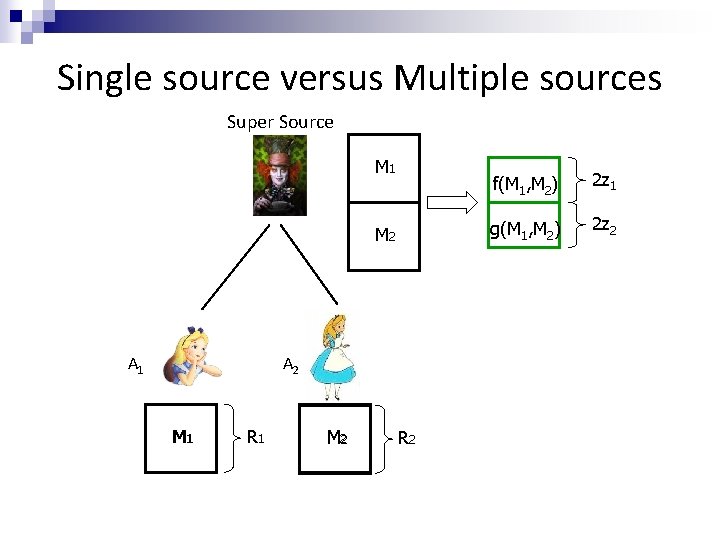
Single source versus Multiple sources Super Source M 1 M 2 A 1 A 2 M 1 R 1 M 2 R 2 f(M 1, M 2) 2 z 1 g(M 1, M 2) 2 z 2

Single source versus Multiple sources Super Source M 1 M 2 A 1 A 2 M 1 R 1 M 2 f(M 1, M 2) 2 z 1 g(M 1, M 2) R 2 2 z 2 f(M 1, M 2) 2 z 1 g(M 1, M 2) 2 z 2

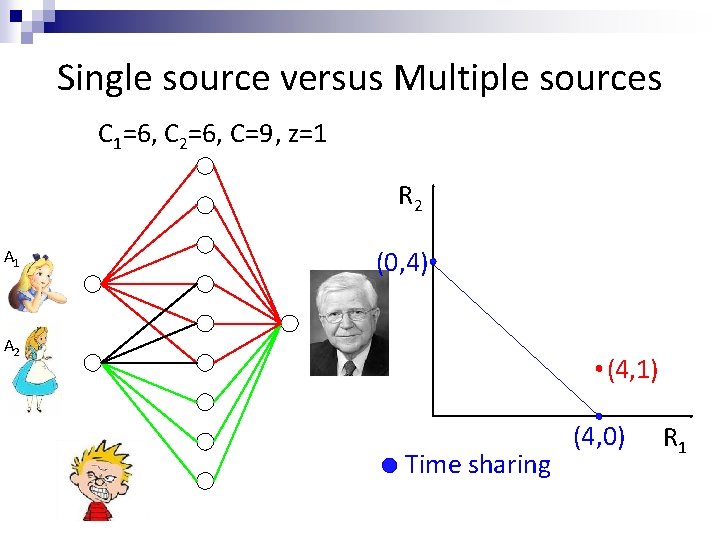
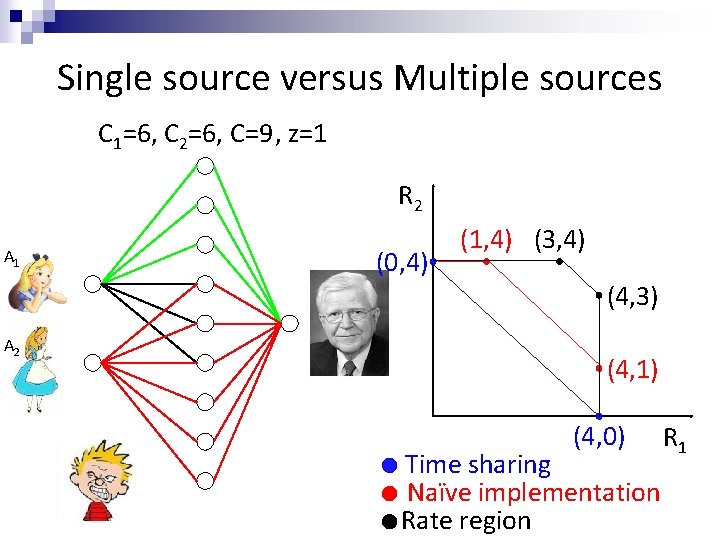
Single source versus Multiple sources C 1=6, C 2=6, C=9, z=1 R 2 A 1 (0, 4) A 2 Time sharing (4, 0) R 1

Single source versus Multiple sources C 1=6, C 2=6, C=9, z=1 R 2 A 1 (0, 4) A 2 (4, 1) Time sharing (4, 0) R 1

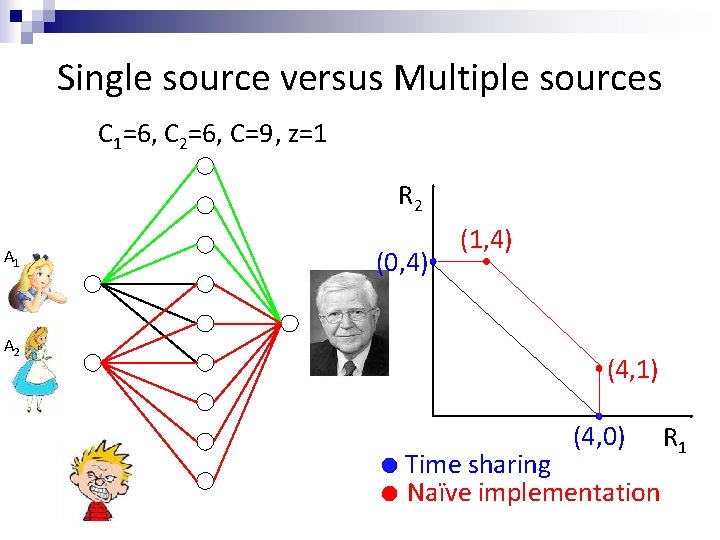
Single source versus Multiple sources C 1=6, C 2=6, C=9, z=1 R 2 A 1 A 2 (0, 4) (1, 4) (4, 1) (4, 0) Time sharing Naïve implementation R 1

Single source versus Multiple sources C 1=6, C 2=6, C=9, z=1 R 2 A 1 A 2 (0, 4) (1, 4) (3, 4) (4, 3) (4, 1) (4, 0) Time sharing Naïve implementation Rate region R 1

Reed Solomon codes Gabidulin codes • Operate over vectors • Operate over matrices • Hamming distance • Rank metric distance • Efficient encoding and decoding

Field Extensions

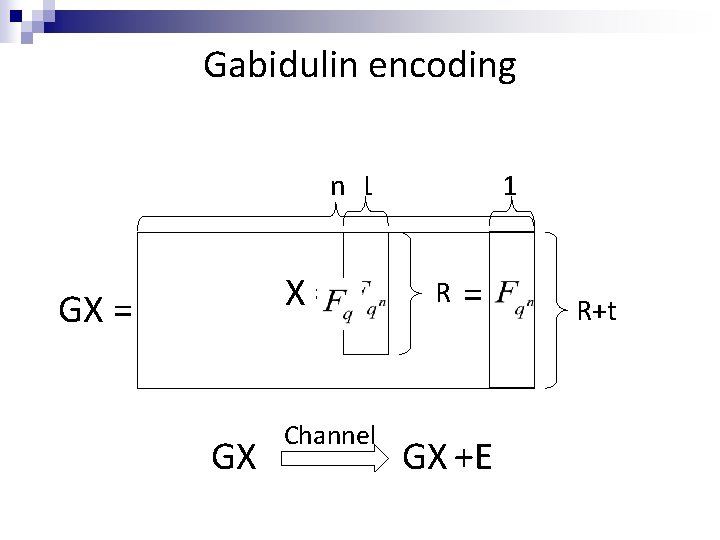
Gabidulin encoding n 1 X= X= R R

Gabidulin encoding n 1 X= GX Channel 1 R = GX +E R+t

Field Extensions Fq. C 2 Fq C Fq

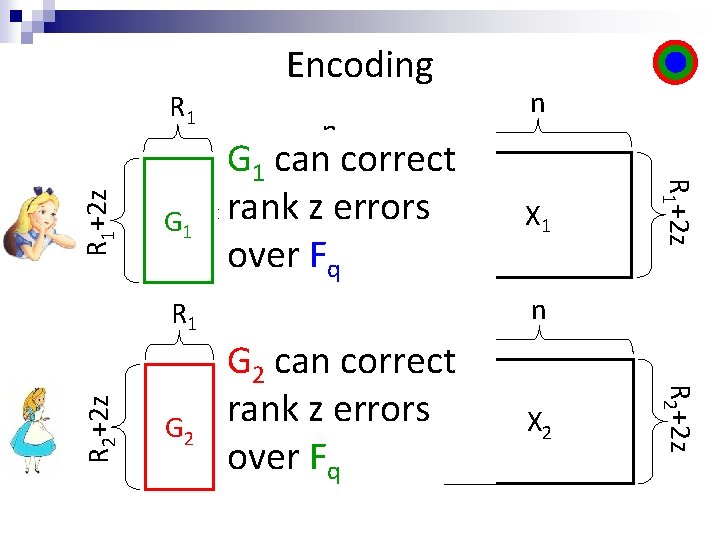
G 1 G 2 G 1 can correct xrank z Merrors = 1 over Fq n G 2 can correct xrank z Merrors = 2 over Fq. C X 1 n X 2 R 2+2 z R 1 n n R 1+2 z R 1 Encoding

Network transmission Y=T 1 G 1 M 1+T 2 G 2 M 2+E

Network transmission Y=T 1 G 1 M 1+T 2 G 2 M 2+E G 1 G 2 (1)

Network transmission G 1 G 2 Y=T 1 G 1 M 1+T 2 G 2 M 2+E G 1 D G 1 G 2 (2) invertible with high probability (1)

Network transmission G 1 G 2 Y=T 1 G 1 M 1+T 2 G 2 M 2+E G 1 D G 1 G 2 (2) invertible with high probability (D-1 Y) = G 2 D-1 E (3) (1)

Network transmission G 1 G 2 Y=T 1 G 1 M 1+T 2 G 2 M 2+E G 1 D G 1 (2) G 2 invertible with high probability (D-1 Y) = (D-1 Y) G 2 D-1 E Lower R +2 z 2 columns (D-1 E) (4) (1)

-1 (D Y) = G 2 M 2 -1 +(D E)

-1 (D Y) = G 2 M 2 -1 +(D E) Matrix with rank 1 over F 2

-1 (D Y) = G 2 M 2 -1 +(D E) Matrix with rank 1 over F 2 Matrix with rank 1 over F 4

-1 (D Y) = G 2 M 2 -1 +(D E) Matrix with rank 1 over F 2 Matrix with rank 1 over F 4 Matrix with rank 2 over F 2 or M 2 can be decoded

Y=T 1 G 1 M 1+T 2 G 2 M 2+E (Y-T 2 G 2 M 2)=T 1 G 1 M 1+E M 1 can be decoded

Questions?

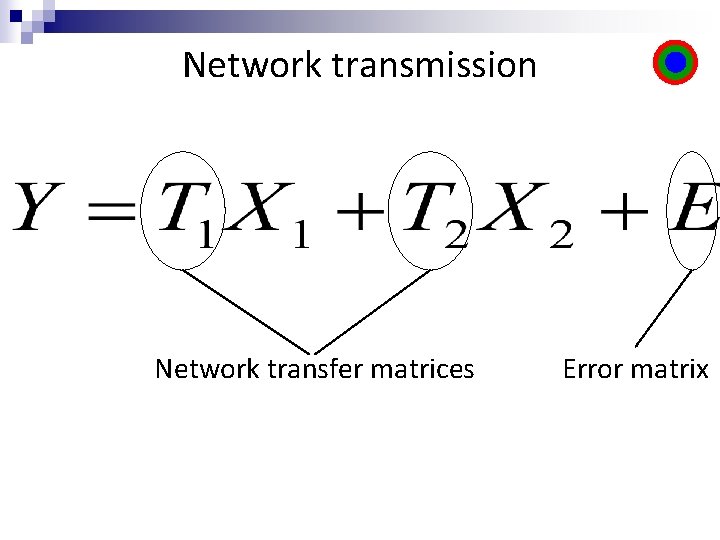
Network transmission Network transfer matrices Error matrix

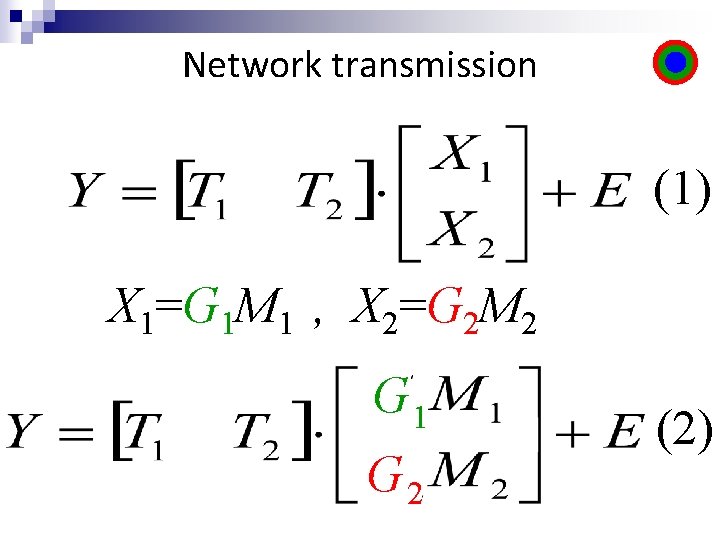
Network transmission (1) X 1=G 1 M 1 , X 2=G 2 M 2

Network transmission (1) X 1=G 1 M 1 , X 2=G 2 M 2

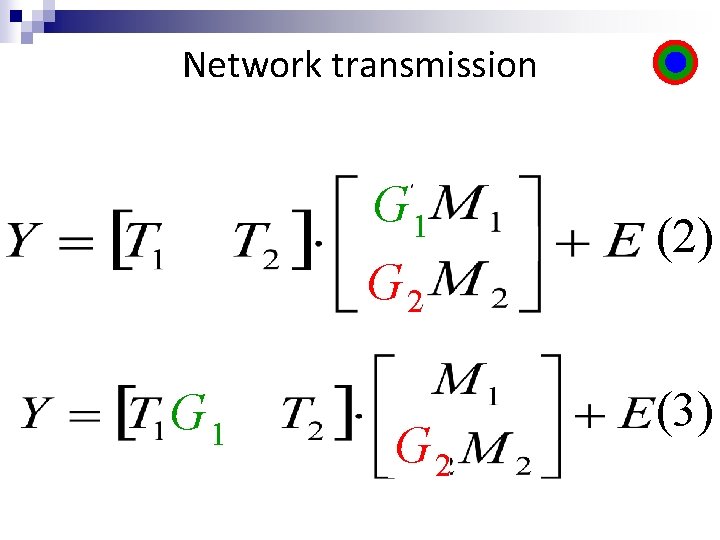
Network transmission (1) X 1=G 1 M 1 , X 2=G 2 M 2 G 1 G 2 (2)

Network transmission G 1 G 2 (2) (3)

Network transmission n T 1, T 2 are the transform matrix from sources 1 and 2 respectively to the receiver. Ti is of dimensions Cx(Ri+2 z) for i={1, 2}. n The receiver gets Error matrix E has rank less than z in F

Decoding of M 2 n T 1, T 2 are the transform matrix from sources 1 and 2 respectively to the receiver. Ti is of dimensions Cx(Ri+2 z) for i={1, 2}. n The receiver gets Error matrix E has rank less than z in F

Decoding of M 2 n T 1, T 2 are the transform matrix from sources 1 and 2 respectively to the receiver. Ti is of dimensions Cx(Ri+2 z) for i={1, 2}. n The receiver gets n Matrix D=[T 1 G 2 T 2] is of dimensions Cx. C over F 1 and invertible with high probability Error matrix E has rank less than z in F

Decoding of M 2 n T 1, T 2 are the transform matrix from sources 1 and 2 respectively to the receiver. Ti is of dimensions Cx(Ri+2 z) for i={1, 2}. n The receiver gets n Matrix D-1 E is of rank no more than z over F 1, but it might have rank more than z over F Error matrix E has rank less than z in F

Decoding of M 2 n T 1, T 2 are the transform matrix from sources 1 and 2 respectively to the receiver. Ti is of Cx(Rover i+2 z) for i={1, 2}. G 2 isdimensions the Gabidulin matrix F 2 that corrects rank z errors even over F 1. n The receiver gets n Matrix D-1 E is of rank no more than z over F 1, but it might have rank more than z over F Error matrix E has rank less than z in F

Non-Coherent Decoding n n Previous construction are for coherence codes, where the receiver knows T 1 and T 2. Non-coherence codes can be achieved by adding headers to each packet R 1+2 Z X 1 = IR 1+2 Z X 2 = O R 2+2 Z n. C 2 O G 1 M 1 R 2+2 Z n. C 2 IR 2+2 Z G 2 M 2 R 1+2 Z over F R 2+2 Z over F

Non-Coherent Decoding n The receiver gets n The receiver computes (over field F 1) where D=[T 1 G 1, T 2], more than z over F 1. and E’ is matrix of rank no

Non-Coherent Decoding n Using invertible rows operation for Ya (over F 1), Bob gets the row-reduced echelon of Ya as: r C V b IC+LU , O C , n. C L: Error Locations, of dimensions C x A. V: Error Values, of dimensions B x n. C. r: Codeword Matrix, of dimensions C x n. C. Let the rank distance between r and X be d. Result: 2 d-a-b<2 z+1 and r=X+ELEV, where EL is of dimensions C x d with the first A columns being L, and EV is of dimensions d x n. C with the last B rows being V. 1 D. Silva, F. Kschischang, and R. Koetter, “A rank-metric approach to error control in random network coding, ” IEEE Tran. on Infor. Theory 2008

Non-Coherent Decoding n Consider the last R 2+2 z rows of r and L, named r’ and L’, respectively. n The row-space distance Drow(r’, G 2 M 2) is also no more than d, and: r’=G 2 M 2+E’LEV, where EL is of dimensions (R 2+2 Z) x d with A columns being L’, and EV is of dimensions d x n. C with B rows being V. n All above matrixes are over the extended field F 1. n Since multiple-field-extension is used, G 2 is over F 2, and able to decode M 2 using r’, L’ and V which are all over F 1. n In the end, similarly subtracting G 2 M 2 from Y, Bob is able to decode M 1.

Comments n The scheme is of polynomial complexity over the size of the network, but of exponential complexity over the number of sources. ¨ For s sources S 1, S 2, …, Ss, the Gabidulin generated matrix of Si must be over finite field Fi to correct rank Z errors over finite filed Fi-1. ¨ Thus, Fi must be the field extension of Fi-1. ¨ In the end, Ss must use Gabidulin generated matrix over field with s extensions from the base field F. n The code construction with polynomial complexity over source numbers is open.

Contribution of this Work n Efficient Multi-source Multicast Error. Correcting Code that: ¨ Achieves the complete rate region; ¨ Each source codes independently; ¨ All internal nodes are oblivious to the code and simply apply random linear network coding. ¨ No information for the network topology is needed (non-coherent coding).