Feng Wang Motivation Training and Testing Pipeline Preliminary

Feng Wang

Motivation •

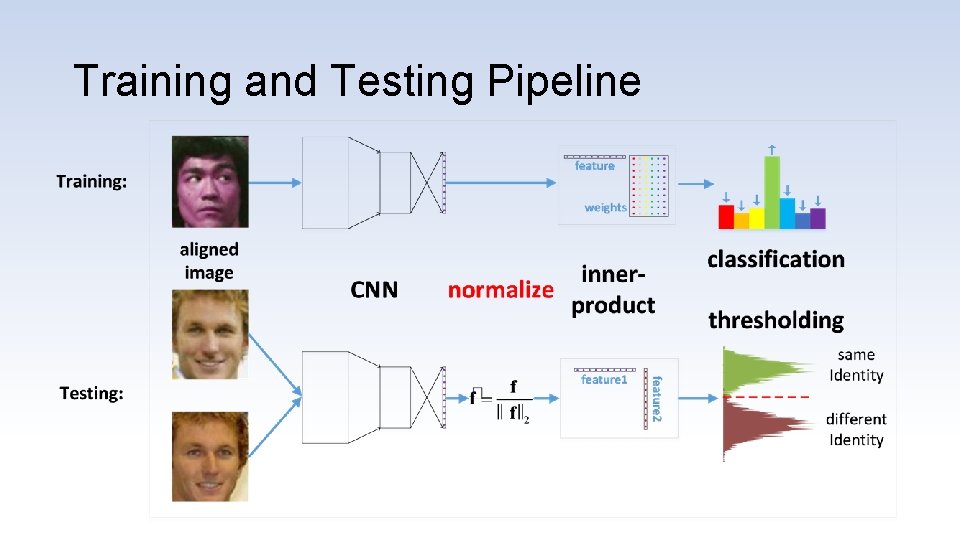
Training and Testing Pipeline

Preliminary Experiments • Normalization term is critical in testing phase. Cosine Similarity: Note: Pretrained model from https: //github. com/ydwen/caffe-face

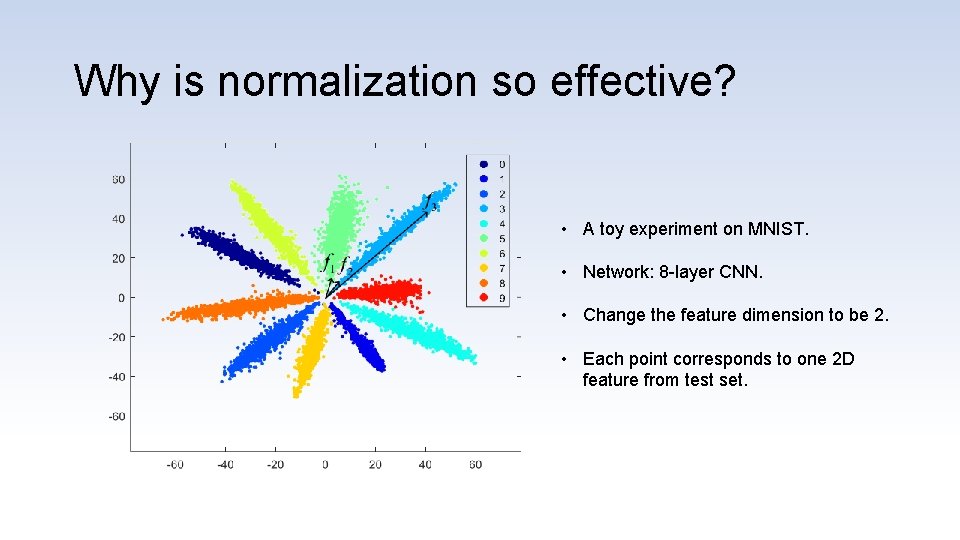
Why is normalization so effective? • A toy experiment on MNIST. • Network: 8 -layer CNN. • Change the feature dimension to be 2. • Each point corresponds to one 2 D feature from test set.

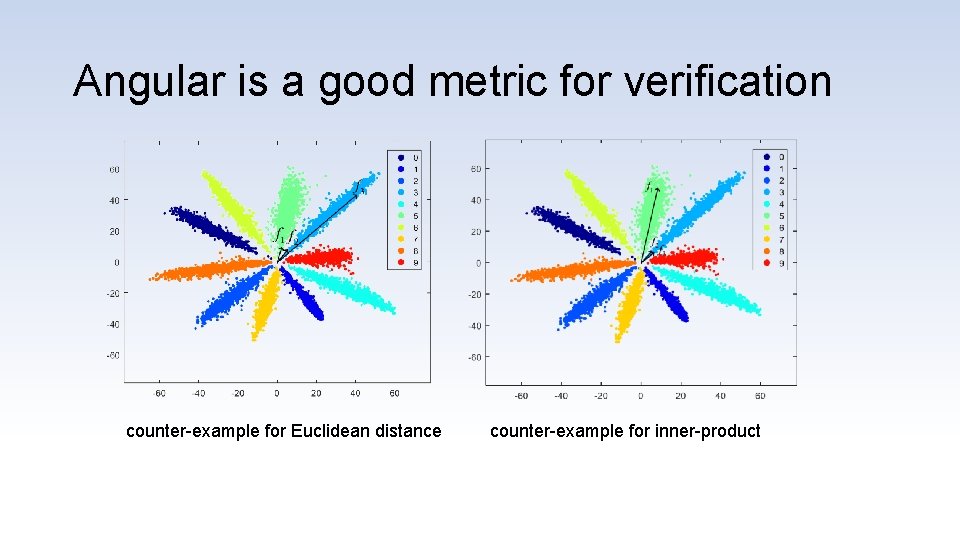
Angular is a good metric for verification counter-example for Euclidean distance counter-example for inner-product

Why is the distribution in this shape?

Softmax is soft-max • argmax operation is scale invariant. • Softmax is the soft version of max.

Norm is related with recognizability Figure credit: L 2 -constrained Softmax Loss for Discriminative Face Verification, Rajeev et al, ar. Xiv 1703. 095

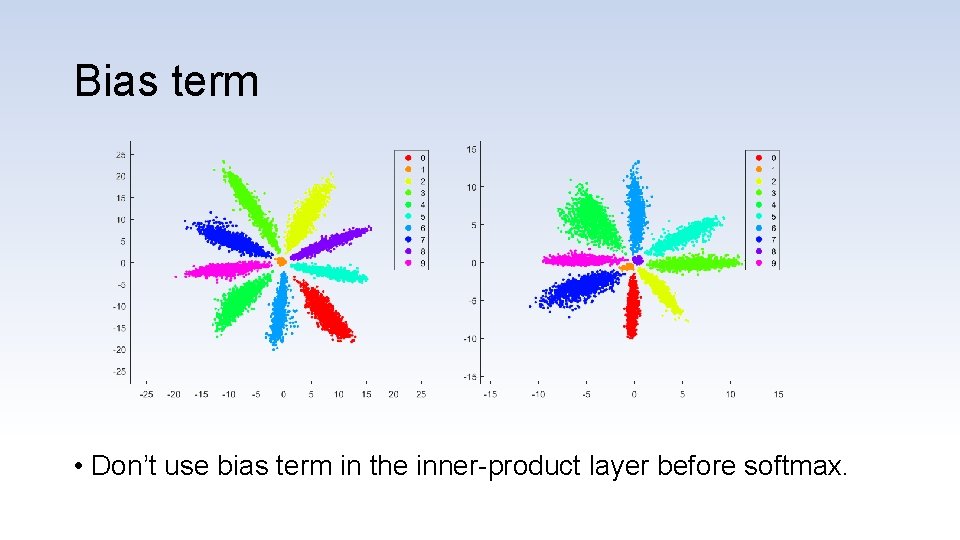
Bias term • Don’t use bias term in the inner-product layer before softmax.

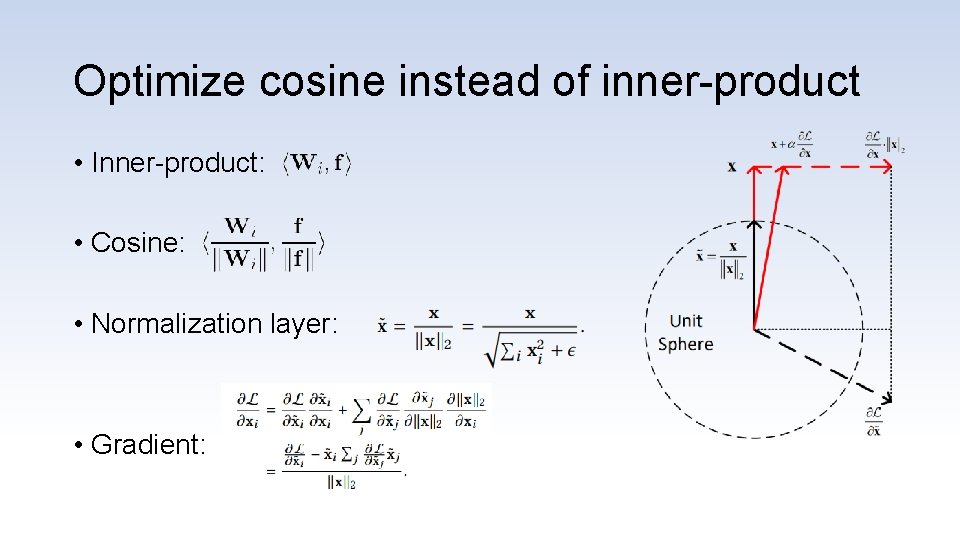
Optimize cosine instead of inner-product • Inner-product: • Cosine: • Normalization layer: • Gradient:

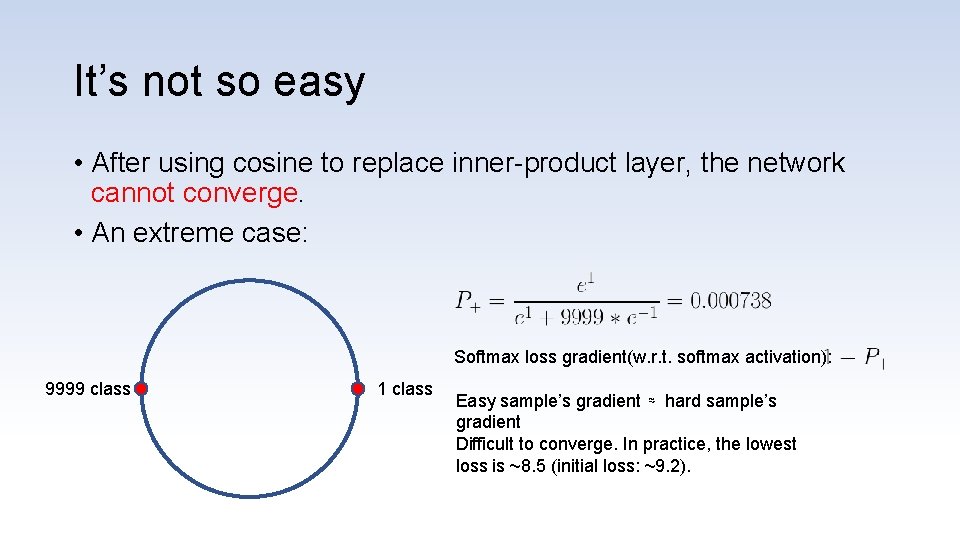
It’s not so easy • After using cosine to replace inner-product layer, the network cannot converge. • An extreme case: Softmax loss gradient(w. r. t. softmax activation): 9999 class 1 class Easy sample’s gradient ≈ hard sample’s gradient Difficult to converge. In practice, the lowest loss is ~8. 5 (initial loss: ~9. 2).

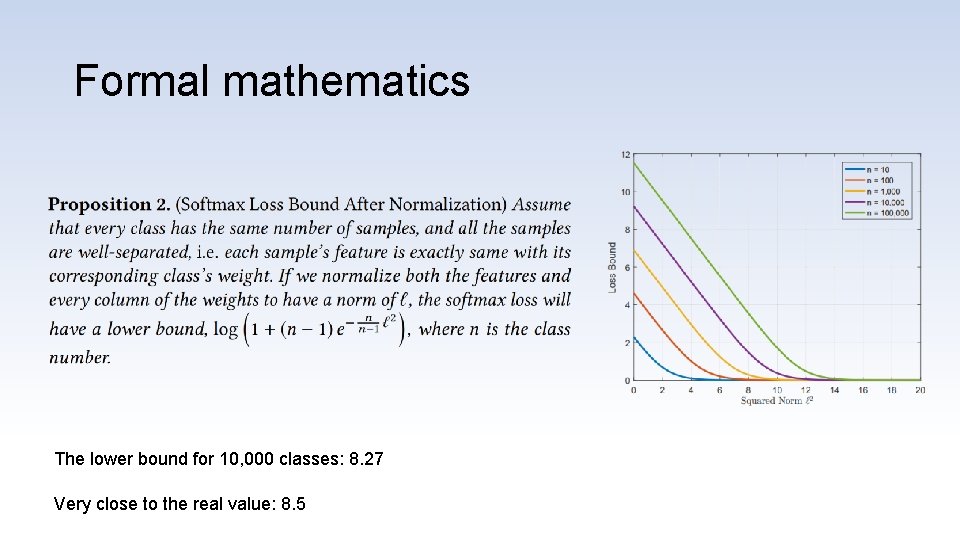
Formal mathematics The lower bound for 10, 000 classes: 8. 27 Very close to the real value: 8. 5

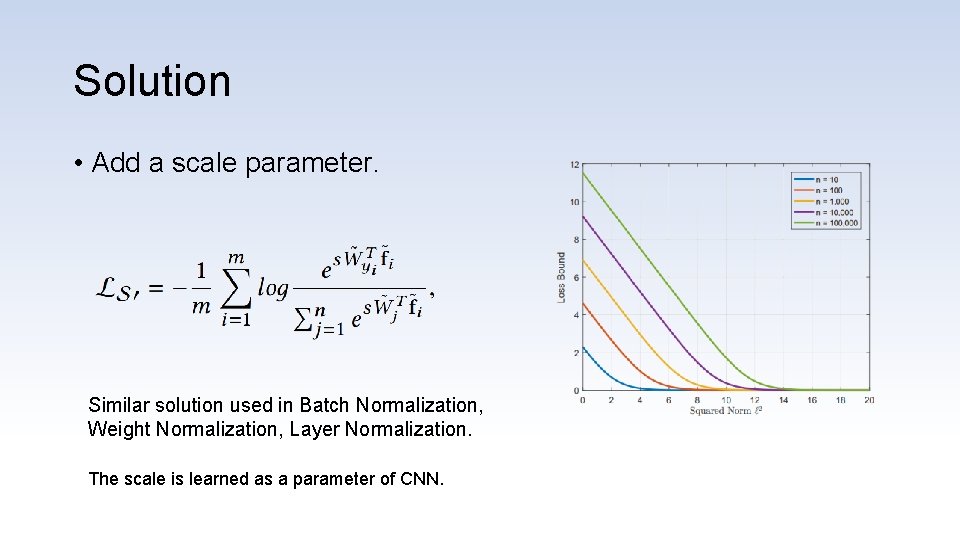
Solution • Add a scale parameter. Similar solution used in Batch Normalization, Weight Normalization, Layer Normalization. The scale is learned as a parameter of CNN.

Another solution • Normalization is very common in metric learning. • Seems that they don’t have converge problem. • Popular metric learning loss functions: • - Contrastive Loss • - Triplet Loss

Metric Learning has sampling problem • When the training sample’s amount is huge, such as 1 Million, we need to train 1 M*1 M pairs to do metric learning. • Usually we need hard mining. • Difficult to implement. • Difficult to tune the hyperparameters.

Re-formulate metric learning loss • Normalized-Softmax: • Reformulate metric learning Contrastive Loss Triplet Loss

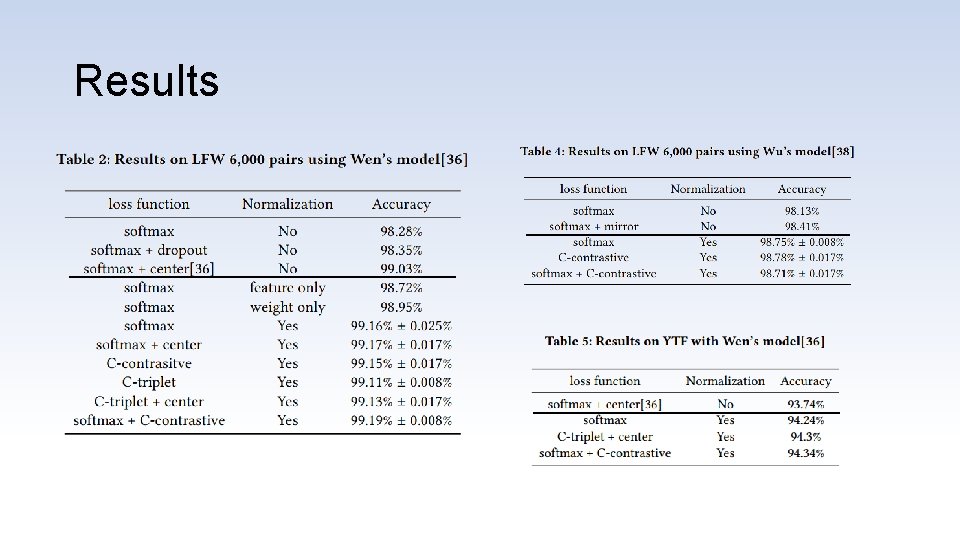
Results

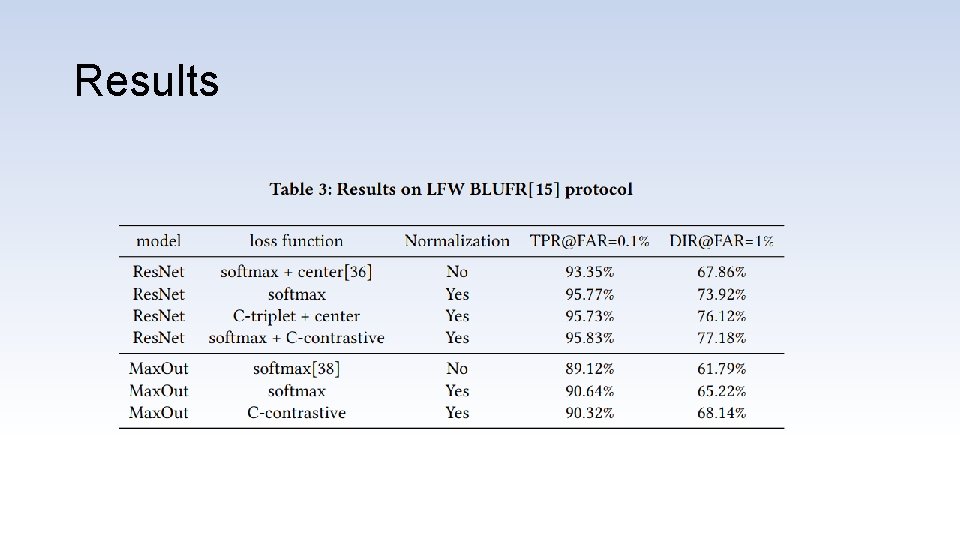
Results

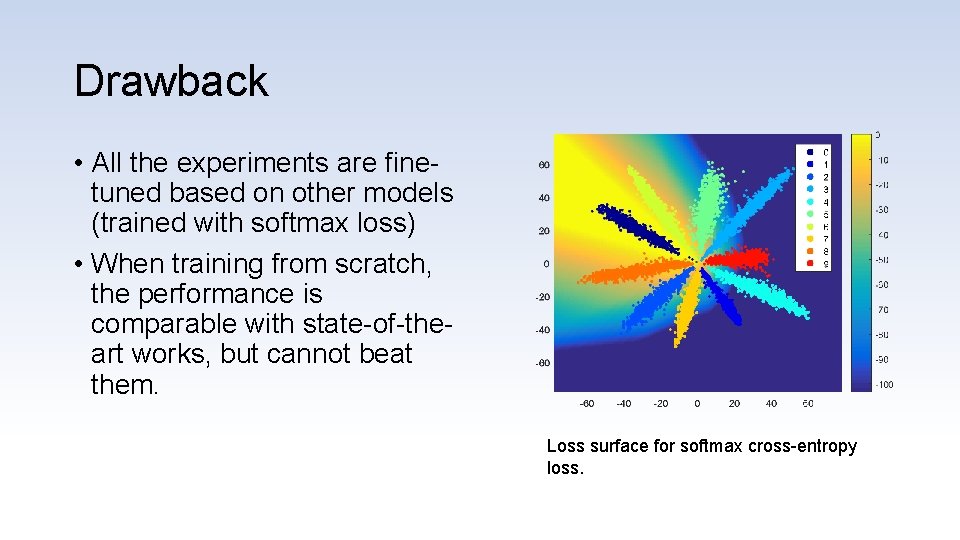
Drawback • All the experiments are finetuned based on other models (trained with softmax loss) • When training from scratch, the performance is comparable with state-of-theart works, but cannot beat them. Loss surface for softmax cross-entropy loss.

Some recent progress

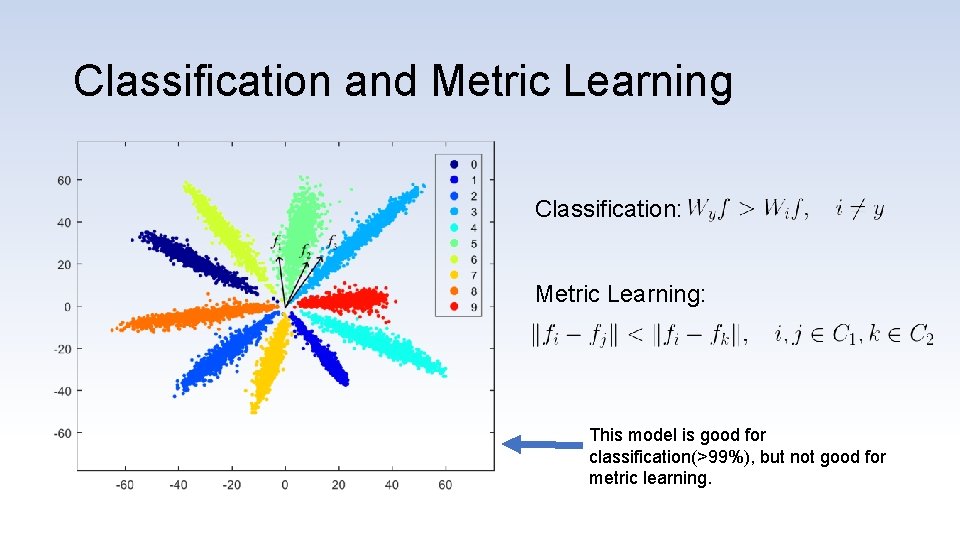
Classification and Metric Learning Classification: Metric Learning: This model is good for classification(>99%), but not good for metric learning.

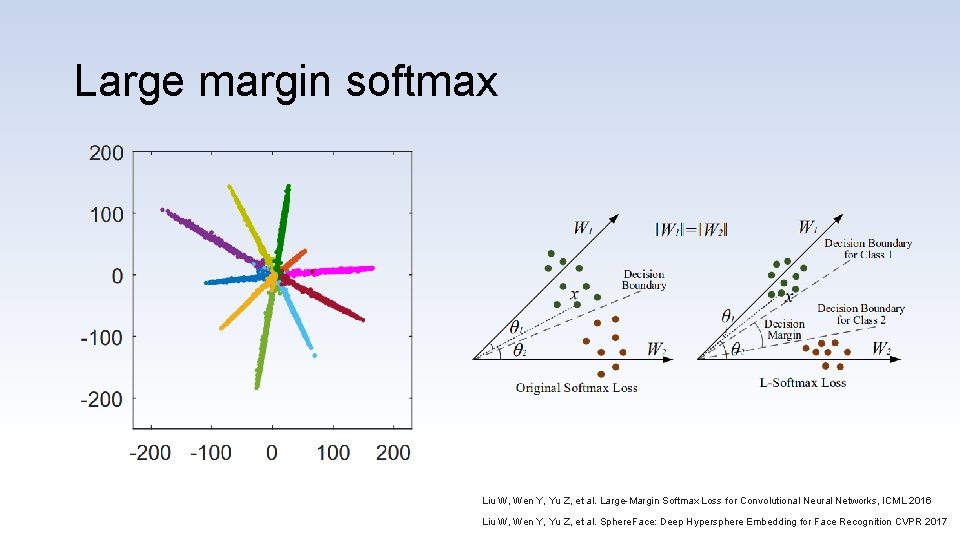
Large margin softmax Liu W, Wen Y, Yu Z, et al. Large-Margin Softmax Loss for Convolutional Neural Networks, ICML 2016 Liu W, Wen Y, Yu Z, et al. Sphere. Face: Deep Hypersphere Embedding for Face Recognition CVPR 2017

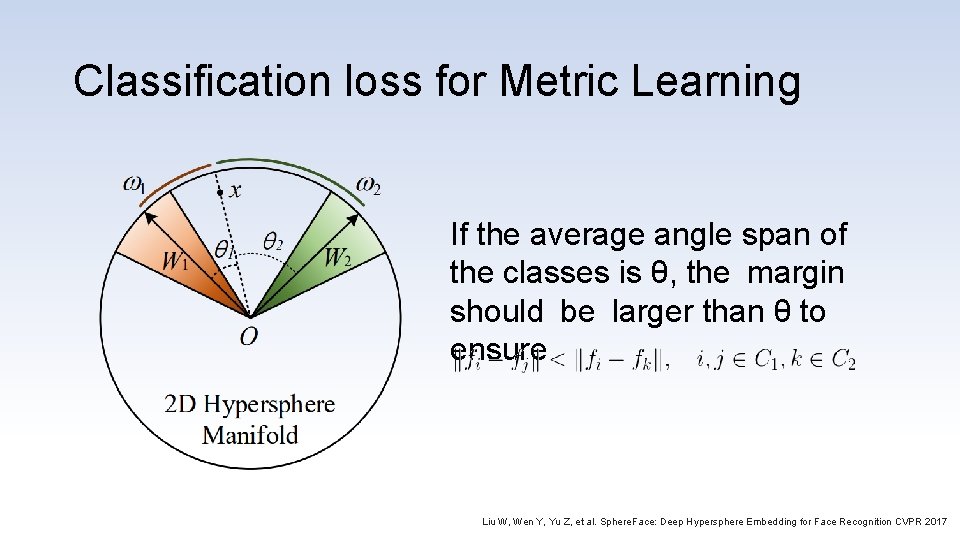
Classification loss for Metric Learning If the average angle span of the classes is θ, the margin should be larger than θ to ensure Liu W, Wen Y, Yu Z, et al. Sphere. Face: Deep Hypersphere Embedding for Face Recognition CVPR 2017

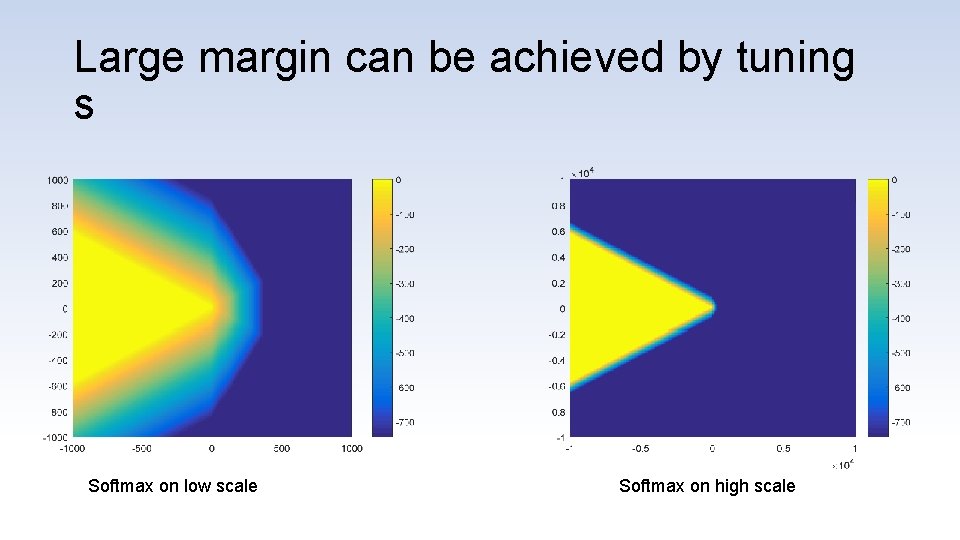
Large margin can be achieved by tuning s s=1 s=7 s=11

Large margin can be achieved by tuning s Softmax on low scale Softmax on high scale

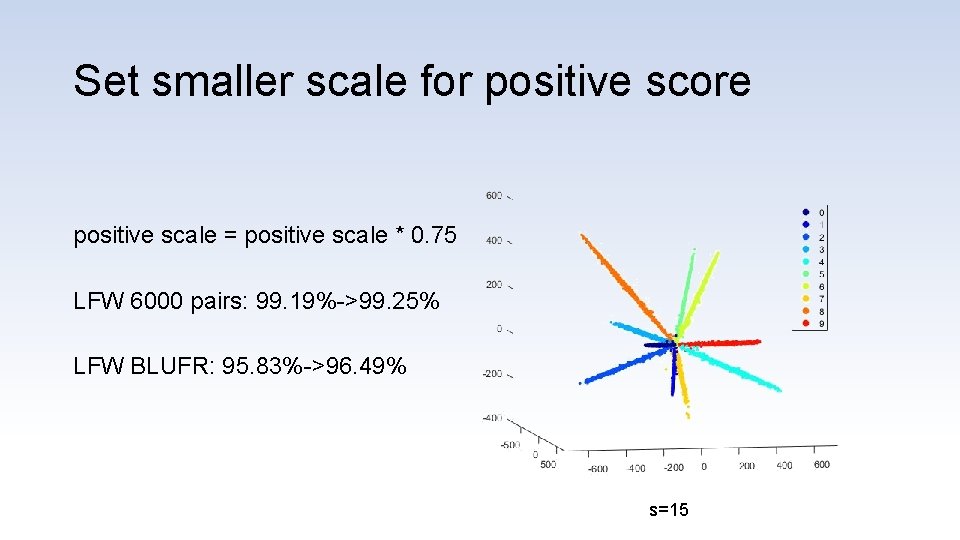
Set smaller scale for positive score positive scale = positive scale * 0. 75 LFW 6000 pairs: 99. 19%->99. 25% LFW BLUFR: 95. 83%->96. 49% s=15