ErrorCorrecting Codes Progress Challenges Madhu Sudan MicrosoftMIT 02172010

Error-Correcting Codes: Progress & Challenges Madhu Sudan Microsoft/MIT 02/17/2010 ECC: Progress/Challenges (@CMU) 1

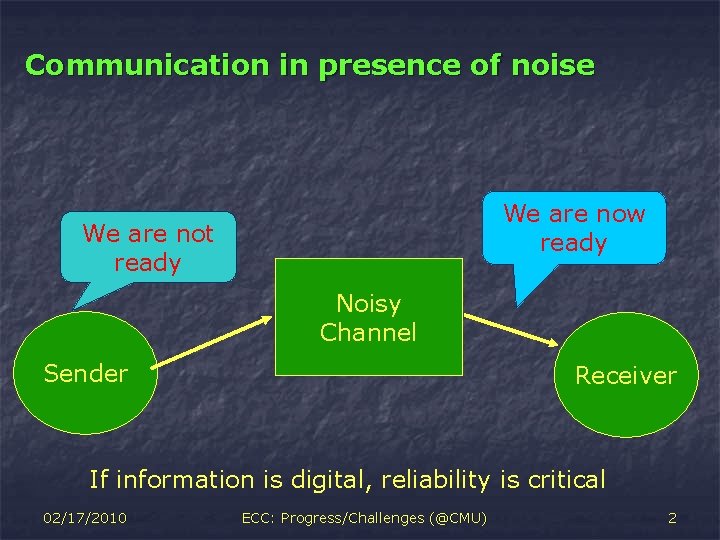
Communication in presence of noise We are now ready We are not ready Noisy Channel Sender Receiver If information is digital, reliability is critical 02/17/2010 ECC: Progress/Challenges (@CMU) 2

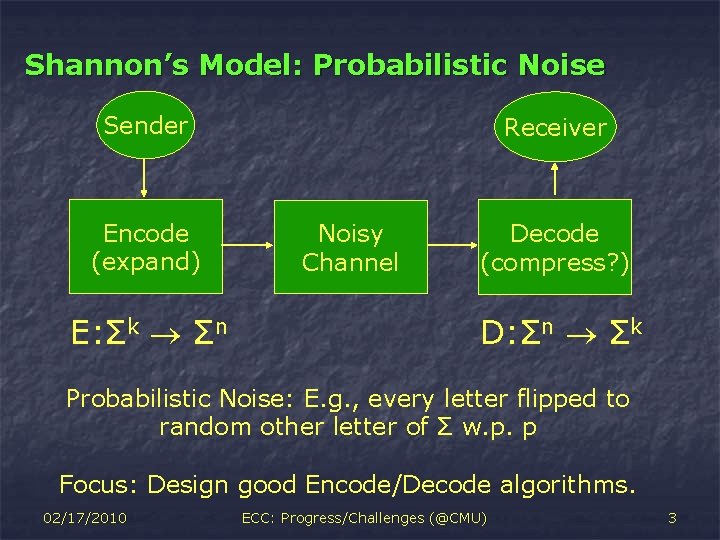
Shannon’s Model: Probabilistic Noise Sender Encode (expand) E: Σk Σn Receiver Noisy Channel Decode (compress? ) D: Σn Σk Probabilistic Noise: E. g. , every letter flipped to random other letter of Σ w. p. p Focus: Design good Encode/Decode algorithms. 02/17/2010 ECC: Progress/Challenges (@CMU) 3

Hamming Model: Worst-case error Errors: Upto t worst-case errors Focus: Code: C = Image(E) = {E(x) | x (Note: Not encoding/decoding) Є Σk } Goal: Design code to correct every possible pattern of t errors. 02/17/2010 ECC: Progress/Challenges (@CMU) 4

Problems in Coding Theory, Broadly n n Combinatorics: Design best possible errorcorrecting codes. Probability/Algorithms: Design algorithms correcting random/worst-case errors. 02/17/2010 ECC: Progress/Challenges (@CMU) 5

Part I (of III): Combinatorial Results 02/17/2010 ECC: Progress/Challenges (@CMU) 6

Hamming Notions Hamming Distance: ¢(x, y) = |{i | xi ≠ yi}| Distance of Code: ¢ (C) = minx, y 2 C {¢ (x, y)} Code of distance 2 t+1 corrects t errors. Main question: Four parameters: Length n, message length k, distance d, alphabet q = |Σ|. - How do they relate? - Want + n, " k, " d, ? q Let: R = k/n; δ= d/n; How do R, δ, q relate? 02/17/2010 ECC: Progress/Challenges (@CMU) 7

Simple results Ball(x, r) = {y in Σn | Δ(x, y) · r} Volume of Ball: Vol(q, n, r) = |Ball(x, r)| Entropy function: Hq(δ) = c s. t. Vol(q, n, δn) ¼ qcn Hamming (Packing) Bound: Balls of radius δn/2 around codewords are disjoint. R + Hq(δ/2) · 1 qk ¢ q. Hq(δ/2)n · qn 02/17/2010 ECC: Progress/Challenges (@CMU) 8

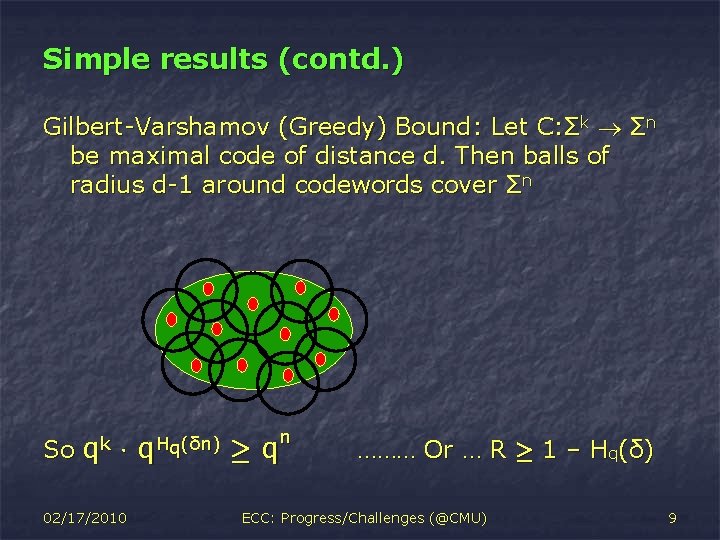
Simple results (contd. ) Gilbert-Varshamov (Greedy) Bound: Let C: Σk Σn be maximal code of distance d. Then balls of radius d-1 around codewords cover Σn So qk ¢ 02/17/2010 q. Hq(δn) n ¸q ……… Or … R ¸ 1 – Hq(δ) ECC: Progress/Challenges (@CMU) 9

Simple results (Summary) For the best code: 1 – H q( δ ) · R · 1 – Hq(δ/2) Which is right? After fifty years of research … We still don’t know. 02/17/2010 ECC: Progress/Challenges (@CMU) 10

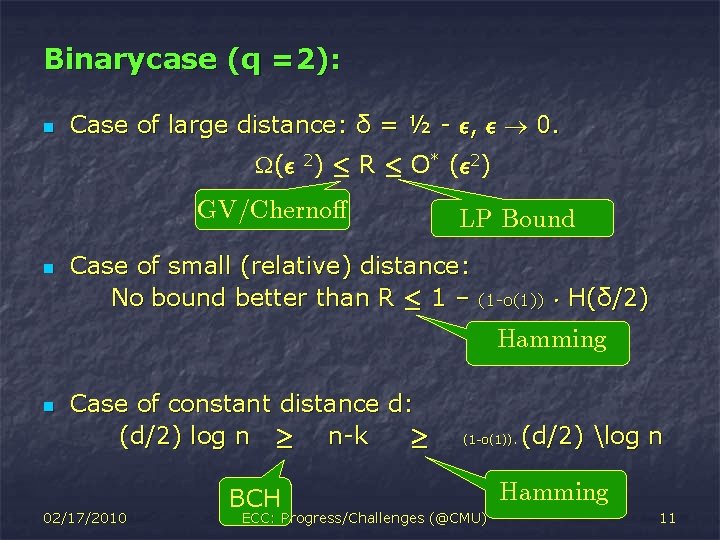
Binary case (q =2): n Case of large distance: δ = ½ - ², ² 0. (² 2) · R · O* (² 2) GV/Cherno® n LP Bound Case of small (relative) distance: No bound better than R · 1 – (1 -o(1)) ¢ H(δ/2) Hamming n Case of constant distance d: (d/2) log n ¸ n-k ¸ 02/17/2010 BCH (1 -o(1)). ECC: Progress/Challenges (@CMU) (d/2) log n Hamming 11

Binary case (Closer look): n n n For general n, d: # Codewords ¸ 2 n / Vol (2, n, d-1) Can we do better? Twice as many codewords? (won’t change asymptotics of R, δ ) Recent progress [Jiang-Vardy]: # Codewords ¸ d ¢ 2 n / Vol(2, n, d-1) 02/17/2010 ECC: Progress/Challenges (@CMU) 12

Major questions in binary codes: n n n Give explicit construction meeting GV bound. n Specifically: Codes with δ = ½ - ² & R = (² 2) Is Hamming tight when δ 0 ? n Do there exist codes of distance δ with R = 1 – [ c ¢ (1 – o(1)) ¢ δ log 2 (1/δ) ] for c < 1? [Hamming: c > ½ ] Is LP Bound tight? 02/17/2010 ECC: Progress/Challenges (@CMU) 14

Combinatorics (contd. ): q-ary case n Fix δ and let q 1 (then fix q and let n 1) 1 – δ – O(1/log q) · R · GV bound n Surprising result (’ 80 s): n n Algebraic Geometry yields: 1 – δ – 1/q Plotkin R ¸ 1 – δ – 1/(√q – 1) (Also a negative surprise: BCH codes only yield 1 – R · (q-1)/q logq n) Not Hamming 02/17/2010 ECC: Progress/Challenges (@CMU) 15

Major questions: q-ary case n n n Suppose R = 1 – δ – f(q) What is the fastest decaying function f(. )? n (somewhere between 1/√q and 1/q). n Give a simple explanation for why f(q) · 1/√q Fix d, and let q 1 n How does (n-k)/(d logq n) grow in the limit? n Is it 1 or ½? Or somewhere in between? 02/17/2010 ECC: Progress/Challenges (@CMU) 16

Part II (of III): Correcting Random Errors 02/17/2010 ECC: Progress/Challenges (@CMU) 17

Recall Shannon ‘ 1948 n n Σ-symmetric channel w. error prob. p: n Transmits σ 2 Σ as σ w. p. 1 -p; and as ¿ 2 Σ- {σ} w. p. p/(q-1). Shannon’s Coding Theorem: n Can transmit at rate R = 1 – Hq(p) - ², 8 ² > 0 If R = 1 – Hq(p) - ², then for every n and k = Rn, there exist E: Σk Σn and D: Σn Σk s. t. Pr. Channel, x [D(Channel(E(x)) ≠ x] · exp(-n). n n Converse Coding Theorem: n Can not transmit at rate R = 1 – Hq(p) + ² So: No mysteries? 02/17/2010 ECC: Progress/Challenges (@CMU) 18

Constructive versions n n n Shannon’s functions: n E random, D brute force search. Can we get poly time E, D? n [Forney 66]: Yes! (Using Reed-Solomon codes correcting ²-fraction error + composition. ) n [Sipser-Spielman ‘ 92, Spielman ‘ 94, Barg. Zemor ‘ 97]: Even in linear time! Still didn’t satisfy practical needs. Why? n [Berrou et al. 92] Turbo codes + belief propagation: n No theorems; Much excitement 02/17/2010 ECC: Progress/Challenges (@CMU) 19

What is satisfaction? n n Articulated by [Luby, Mitzenmacher, Shokrollahi, Spielman ’ 96] Practically interesting question: n = 10000; q = 2, p =. 1; Desired error prob. = 10 -6; k = ? [Forney ‘ 66]: Decoding time: exp(1/(1 – H(p) – (k/n))); n Rate = 90% ) decoding time ¸ 2100; Right question: reduce decoding time to poly(n, 1/ ²); where ² = 1 – H(p) – (k/n) 02/17/2010 ECC: Progress/Challenges (@CMU) 20

Current state of the art n n Luby et al. : Propose study of codes based on irregular graphs (“Irregular LDPC Codes”). No theorems so far for erroneous channels. Strong analysis for (much) simpler case of erasure channels (symbols are erased); decoding time = O(n log (1/²)) (Easy to get “composition” based algorithms with decoding time = O(n poly(1/²)) Do have some proposals for errors as well (with analysis by Luby et al. , Richardson & Urbanke), but none known to converge to Shannon limit. 02/17/2010 ECC: Progress/Challenges (@CMU) 21

Part III: Correcting Adversarial Errors 02/17/2010 ECC: Progress/Challenges (@CMU) 22

Motivation: n n n As notions of communication/storage get more complex, modeling error as oblivious (to message/encoding/decoding) may be too simplistic. Need more general models of error + encoding/decoding for such models. Most pessimistic model: errors are worst-case. 02/17/2010 ECC: Progress/Challenges (@CMU) 23

Gap between worst-case & random errors n n n In Shannon model, with binary channel: n Can correct upto 50% (random) errors. ( 1 -1/q fraction errors, if channel q-ary. ) In Hamming model, for binary channel: n Code with more than n codewords has distance at most 50%. n So it corrects at most 25% worst-case errors. ( ½(1 – 1/q) errors in q-ary case. ) Shannon model corrects twice as many errors: n Need new approaches to bridge gap. 02/17/2010 ECC: Progress/Challenges (@CMU) 24

Approach: List-decoding n n n Main reason for gap between Shannon & Hamming: The insistence on uniquely recovering message. List-decoding: Relaxed notion of recovery from error. Decoder produces small list (of L) codewords, such that it includes message. Code is (p, L) list-decodable if it corrects p fraction error with lists of size L. 02/17/2010 ECC: Progress/Challenges (@CMU) 25

List-decoding n n n Main reason for gap between Shannon & Hamming: The insistence on uniquely recovering message. List-decoding [Elias ’ 57, Wozencraft ’ 58]: Relaxed notion of recovery from error. Decoder produces small list (of L) codewords, such that it includes message. Code is (p, L) list-decodable if it corrects p fraction error with lists of size L. 02/17/2010 ECC: Progress/Challenges (@CMU) 26

What to do with list? n n n Probabilistic error: List has size one w. p. nearly 1 General channel: Need side information of only O(log n) bits to disambiguate [Guruswami ’ 03] n (Alt’ly if sender and receiver share O(log n) bits, then they can disambiguate [Langberg ’ 04]). Computationally bounded error: n Model introduced by [Lipton, Ding Gopalan L. ] n List-decoding results can be extended (assuming PKI and some memory at sender) [Micali et al. ] 02/17/2010 ECC: Progress/Challenges (@CMU) 27

List-decoding: State of the art n n n [Zyablov-Pinsker/Blinovskii – late 80 s] n There exist codes of rate 1 – Hq(p) - epsilon that are (p, O(1))-list-decodable. Matches Shannon’s converse perfectly! (So can’t do better even for random error!) But [ZP/B] non-constructive! 02/17/2010 ECC: Progress/Challenges (@CMU) 28

Algorithms for List-decoding n n n Not examined till ’ 88. First results: [Goldreich-Levin] for “Hadamard’’ codes (non-trivial in their setting). More recent work: n [S. ’ 96, Shokrollahi-Wasserman ’ 98, Guruswami-S. ’ 99, Parvaresh-Vardy ’ 05, Guruswami-Rudra ’ 06] – Decode algebraic codes. n [Guruswami-Indyk ’ 00 -’ 02] theoretic codes. 02/17/2010 – Decode graph- ECC: Progress/Challenges (@CMU) 29

Results in List-decoding n q-ary case: n [Guruswami-Rudra ‘ 06] Codes of rate R correcting 1 – R - ² fraction errors with q = q(²) n Matches Shannon bound (except for q( ²) ) 9 Codes of rate ²c correcting 1 ¡ ² fraction errors. 2 ¡ c = 4: Guruswami et al. 2000 ¡ c ! 3: Implied by Parvaresh-Vardy 05 ¡ c = 3: Guruswami Rudra 02/17/2010 ECC: Progress/Challenges (@CMU) 30

Major open question ² Construct (p; O(1)) list-decodable binary code of rate 1 ¡ H(p) ¡ ² with polytime list decoding. . ² Note: If running time is poly(1=²) then this implies a solution to the random error problem as well. 02/17/2010 ECC: Progress/Challenges (@CMU) 34

Conclusions n n n Coding theory: Very practically motivated problems; solutions influence (if not directly alter) practice. Many mysteries remain in combinatorial setting. Significant progress in algorithmic setting, but many more questions to resolve. 02/17/2010 ECC: Progress/Challenges (@CMU) 35