Electrons w Thermionic Emission w Deflection of Electrons

Electrons w. Thermionic Emission w. Deflection of Electrons in Electric Field w. Deflection of Electrons in Magnetic Field w. Determination of e/m w. Cathode Ray Oscilloscope

Thermionic Emission (1) w When a metal is heated sufficiently, its free electrons gain enough kinetic energy to leave the metal. This process is called thermionic emission.

Thermionic Emission (2) w In practice, thermionic emission is caused by heating a filament of metal wire with an electric current.

Thermionic Emission (3) w The work done on each electron from the filament is W = e. V where V is the p. d. across the filament and the anode. w Electron-volt The electron-volt is an amount of energy equal to the work done on an electron moved through a p. d. of 1 V. 1 electron-volt = J

Properties of Electron Beams (Cathode rays) w Cathode rays travel in straight lines. w Cathode rays can cause fluorescence. w Cathode rays can be deflected by electric field and magnetic field. w Cathode rays may produce heat and X-rays. w Cathode rays can affect photographic plates.

Deflection of Electrons in a Uniform Electric Field (1) w Consider an electron beam directed between two oppositely charged parallel plates as shown below. w With a constant potential difference between the two deflecting plates, the trace is curved towards the positive plate. + d -

Deflection of Electrons in a Uniform Electric Field (2) w The force acting on each electron in the field is given by where E = electric field strength, Vp = p. d. between plates, d = plate spacing.

Deflection of Electrons in a Uniform Electric Field (3) w The vertical displacement y is given by This is the equation for a parabola.

Deflection of Electrons in a Uniform Magnetic Field (1) w The force F acting on an electron in a uniform magnetic field is given by Since the magnetic force F is at right angles to the velocity direction, the electron moves round a circular path.

Deflection of Electrons in a Uniform Magnetic Field (2) w The centripetal acceleration of the electrons is Hence which gives

Determination of Specific Charge - e/m J. J. Thomson

Determination of Specific Charge Using a Fine Beam Tube (1) w The principle of the experiment is illustrated by the diagram below. ×××× Electron gun ×××× F=Bev × ××××× v × × × r× × × ××××

Determination of Specific Charge Using a Fine Beam Tube (2) Since (For an electron moving in a uniform magnetic field) and the kinetic energy of the electron provided by the electron gun is Where V is the anode voltage.

Determination of Specific Charge Using a Fine Beam Tube (3) So Rearrange the equation gives The value of the specific charge of an electron is now known accurately to be C/kg

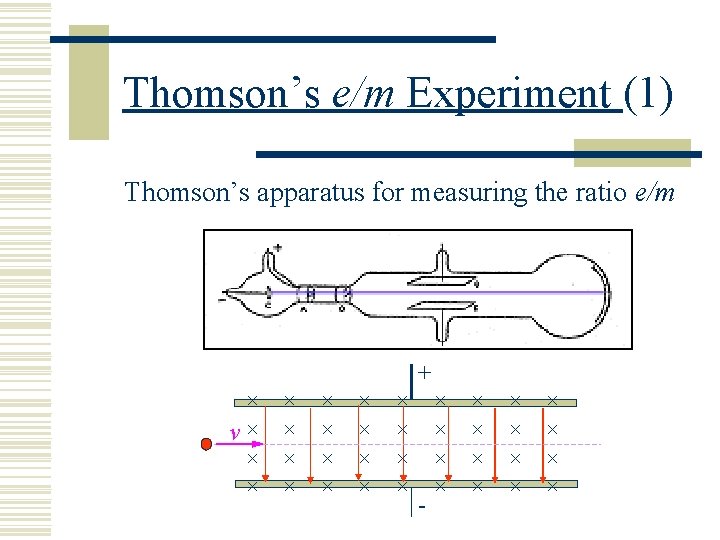
Thomson’s e/m Experiment (1) Thomson’s apparatus for measuring the ratio e/m + × v× × × × × - × × × ×

Thomson’s e/m Experiment (2) w A beam of electron is produced by an electron gun with an accelerating voltage V. w The electron beam is arranged to travel through an electric field and a magnetic field which are perpendicular to each other. w The apparatus is set-up so that an electron from the gun is undeflected.

Thomson’s e/m experiment (3) w As the electron from the gun is undeflected, this gives e. E i. e. On the other hand, Combining the equations, we get v Bev

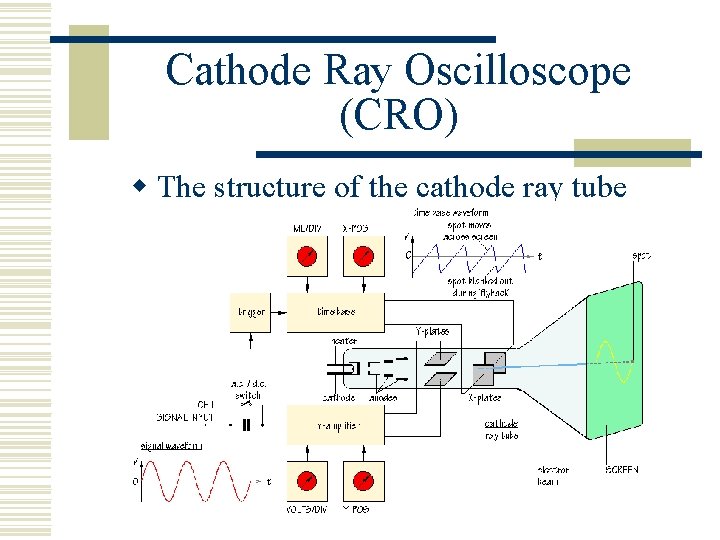
Cathode Ray Oscilloscope (CRO) w The structure of the cathode ray tube

Uses of CRO w An oscilloscope can be used as 1. an a. c. and d. c. voltmeter, 2. for time and frequency measurement, 3. as a display device.

Lissajous’ Figures (1) w Lissajous’ figure can be displayed by applying two a. c. signals simultaneously to the X-plates and Y-plates of an oscilloscope. w As the frequency, amplitude and phase difference are altered, different patterns are seen on the screen of the CRO.

Lissajous’ Figures (2) Same amplitude but different frequencies

Lissajous’ Figures (3) Same frequency but different phase In phase π /4 π/2 π 3π/4 3π/2 5π/4 In phase 7π/2 http: //surendranath. tripod. com/Lissajous. html