ELEC 5270 0016270 001 Fall 2006 LowPower Design

ELEC 5270 -001/6270 -001 (Fall 2006) Low-Power Design of Electronic Circuits (Formerly ELEC 5970 -003/6970 -003) Linear Programming – A Mathematical Optimization Technique Vishwani D. Agrawal James J. Danaher Professor Department of Electrical and Computer Engineering Auburn University, Auburn, AL 36849 http: //www. eng. auburn. edu/~vagrawal@eng. auburn. edu Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 1

What is Linear Programming n n Linear programming (LP) is a mathematical method for selecting the best solution from the available solutions of a problem. Method: State the problem and define variables whose values will be determined. n Develop a linear programming model: n n Write the problem as an optimization formula (a linear expression to be minimized or maximized) Write a set of linear constraints An available LP solver (computer program) gives the values of variables. Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 2

Types of LPs n n LP – all variables are real. ILP – all variables are integers. MILP – some variables are integers, others are real. A reference: n S. I. Gass, An Illustrated Guide to Linear Programming, New York: Dover, 1990. Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 3

A Single-Variable Problem n n n Consider variable x Problem: find the maximum value of x subject to constraint, 0 ≤ x ≤ 15. Solution: x = 15. Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 4

Single Variable Problem (Cont. ) n n Consider more complex constraints: Maximize x, subject to following constraints n n x≥ 0 5 x ≤ 75 6 x ≤ 30 x ≤ 10 0 (1) (2) (3) (4) 5 10 (3) 15 x (2) (1) (4) All constraints satisfied Solution, x = 5 Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 5

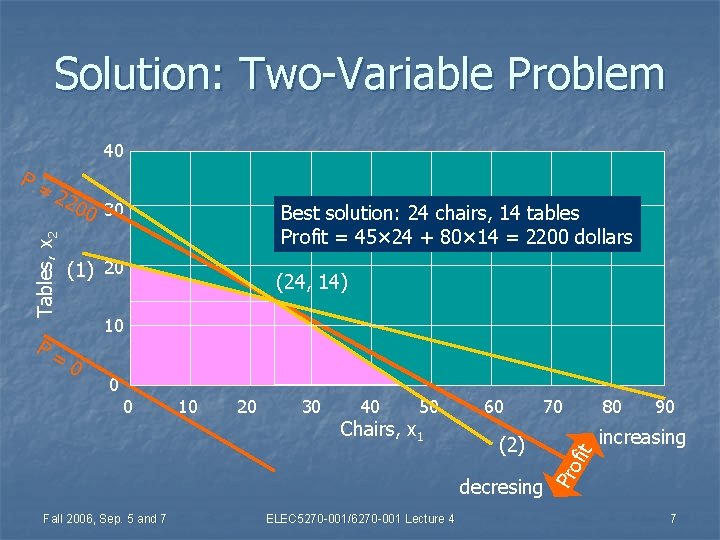
A Two-Variable Problem n Manufacture of x 1 chairs and x 2 tables: Maximize profit, P = 45 x 1 + 80 x 2 dollars n Subject to resource constraints: n 400 boards of wood, 5 x 1 + 20 x 2 ≤ 400 n 450 man-hours of labor, 10 x 1 + 15 x 2 ≤ 450 n x 1 ≥ 0 n x 2 ≥ 0 n Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 (1) (2) (3) (4) 6

Solution: Two-Variable Problem 40 22 Best solution: 24 chairs, 14 tables Profit = 45× 24 + 80× 14 = 2200 dollars (1) 20 (24, 14) 10 0 10 20 30 40 50 Chairs, x 1 60 70 (2) decresing Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 80 90 increasing fit P= 00 30 Pro Tables, x 2 P= 7

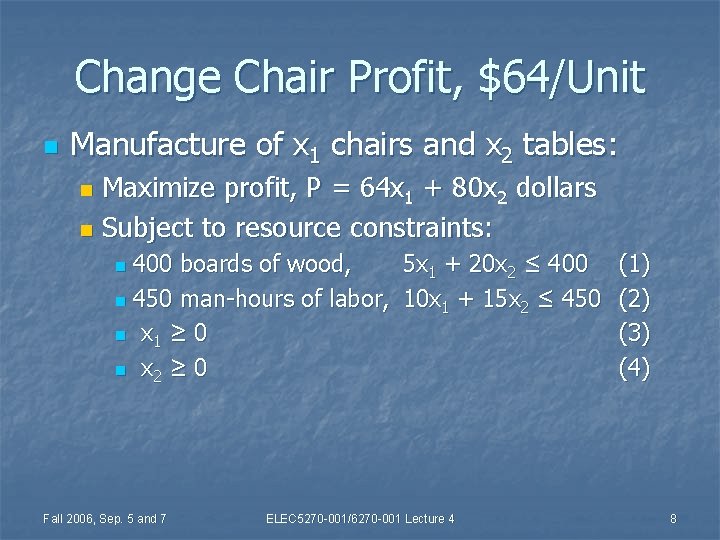
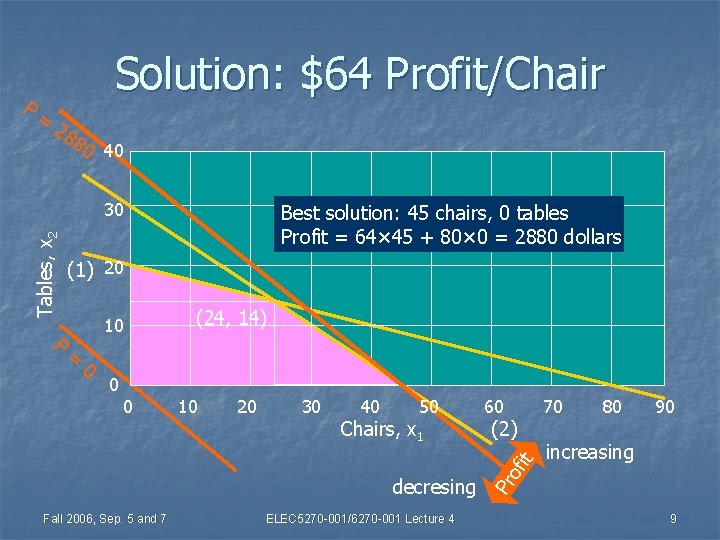
Change Chair Profit, $64/Unit n Manufacture of x 1 chairs and x 2 tables: Maximize profit, P = 64 x 1 + 80 x 2 dollars n Subject to resource constraints: n 400 boards of wood, 5 x 1 + 20 x 2 ≤ 400 n 450 man-hours of labor, 10 x 1 + 15 x 2 ≤ 450 n x 1 ≥ 0 n x 2 ≥ 0 n Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 (1) (2) (3) (4) 8

= 28 80 40 30 Tables, x 2 P Best solution: 45 chairs, 0 tables Profit = 64× 45 + 80× 0 = 2880 dollars (1) 20 10 = 0 (24, 14) 0 10 20 30 40 50 Chairs, x 1 60 (2) decresing Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 70 80 90 increasing of it 0 Pr P Solution: $64 Profit/Chair 9

Primal-Dual Problems n n Primal problem Variables: n n n x 1 (number of chairs) x 2 (number of tables) n n n 5 x 1 + 20 x 2 10 x 1 + 15 x 2 x 1 x 2 n n n w 1 ($ cost/board of wood) w 2 ($ cost/man-hour) Minimize cost 400 w 1 + 450 w 2 Subject to: n n n x 1 = 24 chairs, x 2 = 14 tables Profit = $2200 Fall 2006, Sep. 5 and 7 n ≥ 400 ≥ 450 ≥ 0 Solution: n Dual Problem Variables: n Maximize profit 45 x 1 + 80 x 2 Subject to: n n n 5 w 1 +10 w 2 20 w 1 + 15 w 2 w 1 w 2 ≥ 45 ≥ 80 ≥ 0 Solution: n n w 1 = $1, w 2 = $4 Cost = $2200 ELEC 5270 -001/6270 -001 Lecture 4 10

The Duality Theorem n If the primal has a finite optimal solution, so does the dual, and the optimum values of the objective functions are equal. Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 11

LP for n Variables n minimize Σ cj xj Objective function j =1 n subject to Σ aij xj ≤ bi, i = 1, 2, . . . , m j =1 n Σ cij xj = di, i = 1, 2, . . . , p j =1 Variables: xj Constants: cj, aij, bi, cij, di Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 12

Algorithms for Solving LP n Simplex method n n Ellipsoid method n n L. G. Khachiyan, “A Polynomial Algorithm for Linear Programming, ” Soviet Math. Dokl. , vol. 20, pp. 191 -194, 1984. Interior-point method n n G. B. Dantzig, Linear Programming and Extension, Princeton, New Jersey, Princeton University Press, 1963. N. K. Karmarkar, “A New Polynomial-Time Algorithm for Linear Programming, ” Combinatorica, vol. 4, pp. 373 -395, 1984. Course website of Prof. Lieven Vandenberghe (UCLA), http: //www. ee. ucla. edu/ee 236 a. html Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 13

Basic Ideas of Solution methods Extreme points Constraints Extreme points Objective function Simplex: search on extreme points. Fall 2006, Sep. 5 and 7 Constraints Objective function Interior-point methods: Successively iterate with interior spaces of analytic convex boundaries. ELEC 5270 -001/6270 -001 Lecture 4 14

Integer Linear Programming (ILP) n n n Variables are integers. Complexity is exponential – higher than LP. LP relaxation Convert all variables to real, preserve ranges. n LP solution provides guidance. n Rounding LP solution can provide a non-optimal solution. n Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 15

ILP Example: Test Minimization n n A combinational circuit has n test vectors that detect m faults. Each test detects a subset of faults. Find the smallest subset of test vectors that detects all m faults. ILP model: n n Assign an integer ti ε [0, 1] variable to ith test vector such that ti = 1, if we select ti, otherwise ti= 0. Define an integer constant fij ε [0, 1] such that fij = 1, if ith vector detects jth fault, otherwise fij = 0. Values of constants fij are determined by fault simulation. Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 16

Test Minimization by ILP n minimize Σ ti Objective function i=1 n subject to Σ fij ti ≥ 1, j = 1, 2, . . . , m i=1 Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 17

3 V 3 F: A 3 -Vector 3 -Fault Example Test vector i fij i=1 i=2 i=3 Variables: t 1, t 2, t 3 ε [0, 1] Fault j Minimize t 1 + t 2 + t 3 j=1 1 1 0 j=2 0 1 1 Subject to: t 1 + t 2 ≥ 1 t 2 + t 3 ≥ 1 j=3 Fall 2006, Sep. 5 and 7 1 0 1 ELEC 5270 -001/6270 -001 Lecture 4 t 1 + t 3 ≥ 1 18

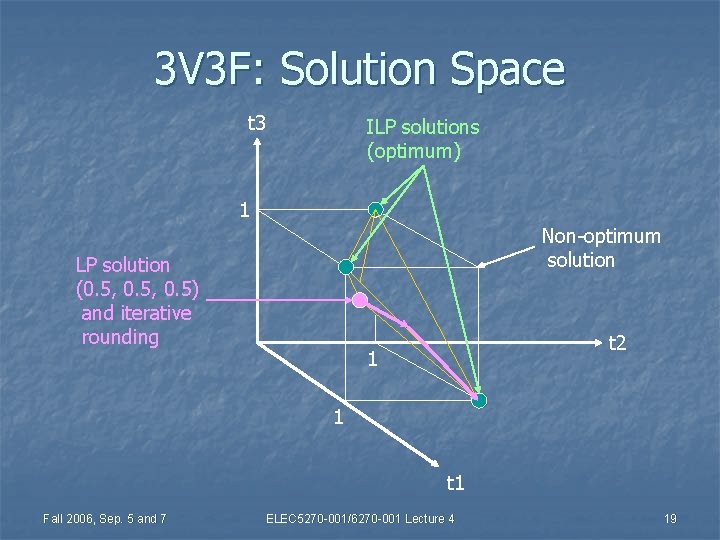
3 V 3 F: Solution Space t 3 ILP solutions (optimum) 1 Non-optimum solution LP solution (0. 5, 0. 5) and iterative rounding t 2 1 1 t 1 Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 19

Characteristics of ILP n n n Worst-case complexity is exponential in number of variables. Linear programming (LP) relaxation, where integer variables are treated as real, gives a lower bound on the objective function. Recursive rounding of relaxed LP solution to nearest integers gives an approximate solution to the ILP problem. n K. R. Kantipudi and V. D. Agrawal, “A Reduced Complexity Algorithm for Minimizing N-Detect Tests, ” Proc. 20 th International Conf. VLSI Design, January 2007, pp. 492 -497. Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 20

3 V 3 F: LP Relaxation and Rounding ILP – Variables: t 1, t 2, t 3 ε [0, 1] LP relaxation: t 1, t 2, t 3 ε (0. 0, 1. 0) Minimize t 1 + t 2 + t 3 Solution: t 1 = t 2 = t 3 = 0. 5 Subject to: Iterative rounding: t 1 + t 2 ≥ 1 t 2 + t 3 ≥ 1 t 1 + t 3 ≥ 1 (1) round one variable, t 1 = 1. 0 (2) Two-variable LP problem: (3) Minimize t 2 + t 3 (4) subject to t 2 + t 3 ≥ 1. 0 (5) LP solution t 2 = t 3 = 0. 5 (6)(2) round a variable, t 2 = 1. 0 (7) ILP constraints are satisfied solution is t 1 = 1, t 2 = 1, t 3 = 0 Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 21

Recursive Rounding Algorithm 1. Obtain a relaxed LP solution. Stop if each variable in the solution is an integer. 2. Round the variable closest to an integer. 3. Remove any constraints that are now unconditionally satisfied. 4. Go to step 1. Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 22

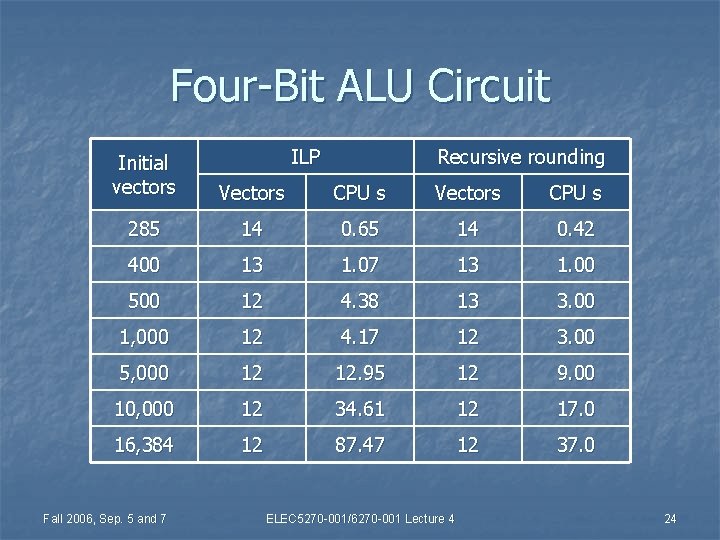
Recursive Rounding n n ILP has exponential complexity. Recursive rounding: ILP is transformed into k LPs with progressively reducing number of variables. n Number of LPs, k, is the size of the final solution, i. e. , the number of non-zero variables in the test minimization problem. n Recursive rounding complexity is k × O(np), where k ≤ n, n is number of variables. n Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 23

Four-Bit ALU Circuit ILP Recursive rounding Initial vectors Vectors CPU s 285 14 0. 65 14 0. 42 400 13 1. 07 13 1. 00 500 12 4. 38 13 3. 00 1, 000 12 4. 17 12 3. 00 5, 000 12 12. 95 12 9. 00 10, 000 12 34. 61 12 17. 0 16, 384 12 87. 47 12 37. 0 Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 24

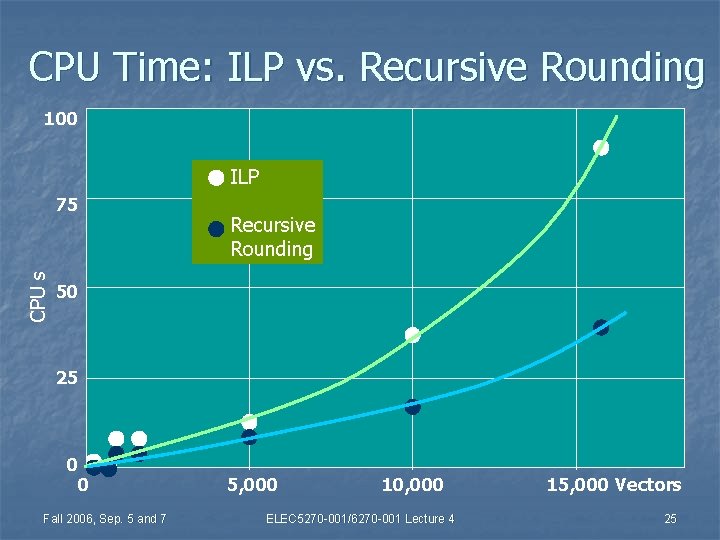
CPU Time: ILP vs. Recursive Rounding 100 ILP CPU s 75 Recursive Rounding 50 25 0 0 Fall 2006, Sep. 5 and 7 5, 000 10, 000 ELEC 5270 -001/6270 -001 Lecture 4 15, 000 Vectors 25

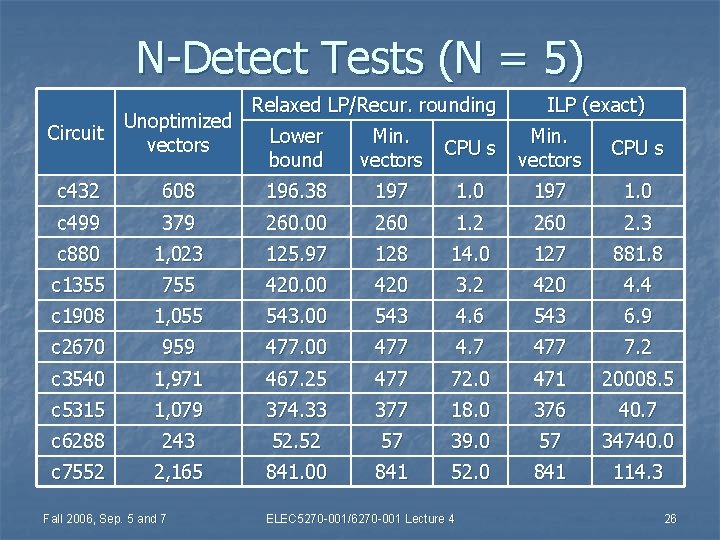
N-Detect Tests (N = 5) Circuit Unoptimized vectors c 432 Relaxed LP/Recur. rounding ILP (exact) Lower bound Min. vectors CPU s 608 196. 38 197 1. 0 c 499 379 260. 00 260 1. 2 260 2. 3 c 880 1, 023 125. 97 128 14. 0 127 881. 8 c 1355 755 420. 00 420 3. 2 420 4. 4 c 1908 1, 055 543. 00 543 4. 6 543 6. 9 c 2670 959 477. 00 477 4. 7 477 7. 2 c 3540 1, 971 467. 25 477 72. 0 471 20008. 5 c 5315 1, 079 374. 33 377 18. 0 376 40. 7 c 6288 243 52. 52 57 39. 0 57 34740. 0 c 7552 2, 165 841. 00 841 52. 0 841 114. 3 Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 26

Finding LP/ILP Solvers n n n R. Fourer, D. M. Gay and B. W. Kernighan, AMPL: A Modeling Language for Mathematical Programming, South San Francisco, California: Scientific Press, 1993. Several of programs described in this book are available to Auburn users. MATLAB? Search the web. Many programs with small number of variables can be downloaded free. Fall 2006, Sep. 5 and 7 ELEC 5270 -001/6270 -001 Lecture 4 27